Эконометрика. Моделирование социально-экономических систем

1.

Православный Свято-Тихоновский гуманитарный университет
Факультет информатики и прикладной математики
Кафедра экономики
ЭКОНОМЕТРИКА
Доцент Долина Ольга Николаевна
2023-2024 уч. год

2.

Тема 2: Моделирование социально-экономических систем
ПЛАН:
1.
2.
3.
4.
5.
Основные аспекты эконометрического моделирования
Этапы эконометрического моделирования
Виды зависимости между случайными величинами
Парный регрессионный анализ
Предпосылки классической линейной модели парной регрессии

3.

1. Основные аспекты эконометрического моделирования
Моделирование - процесс построения, изучения и применения моделей.
Математическое моделирование - средство исследования процессов или явлений с
помощью их математических моделей.
Под моделью понимается физический или абстрактный объект, свойства которого в
определенном смысле сходны со свойствами исследуемого объекта
Модель – объект любой природы, который создается исследователем с целью
получения новых знаний об объекте-оригинале и отражает только существенные
(с точки зрения разработчика) свойства оригинала.
Эконометрическая модель – вероятностно-статистическая модель, описывающая
механизм функционирования экономической или социально –экономической системы
Модель адекватна объекту-оригиналу – если она с достаточной степенью точности
приближения отражает закономерности процесса функционирования реального
объекта.

4.

Моделирование предполагает работы по двум основным направлениям:
- разработка модели;
- исследование модели и получение выводов.
Экзогенные переменные в модели – переменные, задаваемые «извне»,
автономно от модели, управляемые и планируемые.
Экзогенные
(внешние)
переменные
–
макроэкономические
инструменты - бюджетно-налоговая (фискальная) и денежно-кредитная
(монетарная) политика.
Эндогенные переменные модели – переменные, значения которых
формируются в процессе и внутри функционирования анализируемой
социально-экономической системы в значительной степени под
воздействием экзогенных переменных и во взаимодействии друг с другом.
В эконометрическом моделировании они являются предметом
объяснения.
Эндогенные (внутренние) переменные - занятость, выпуск, инфляция,
инвестиции и т.д.

5.

Важной проблемой в процессе эконометрического моделирования является
проблема спецификации модели, в частности:
- выражение в математической форме обнаруженных связей и соотношений;
- установление состава экзогенных и эндогенных переменных, в том числе
лаговых;
- формулировка исходных предпосылок и ограничений модели.
От того, насколько удачно решена проблема спецификации модели, в
значительной степени зависит успех всего эконометрического моделирования.

6.

Требования к моделям:
1) адекватность – достаточно точное отображение свойств объекта;
2) полнота – предоставление получателю всей необходимой информации
об объекте;
3) гибкость – возможность воспроизведения различных ситуаций во всем
диапазоне изменения условий и параметров;
4) трудоемкость разработки должна быть приемлемой для имеющегося
времени и программных средств.

7.

Принципы построения математических моделей:
1. Принцип информационной достаточности. При полном отсутствии информации об
исследуемой системе построение ее модели невозможно. При наличии полной
информации о системе ее моделирование лишено смысла.
2. Принцип осуществимости. Создаваемая модель должна обеспечивать достижение
поставленной цели исследования с вероятностью, существенно отличающейся от нуля,
и за конечное время.
3. Принцип множественности моделей. Данный принцип является ключевым создаваемая модель должна отражать в первую очередь те свойства реальной системы
(или явления), которые влияют на выбранный показатель эффективности.
4. Принцип агрегирования - сложную систему можно представить состоящей из
агрегатов (подсистем).
5. Принцип параметризации - подсистемы можно заменять в модели

8.

Общим моментом для любой эконометрической модели является
разбиение зависимой переменной на две части — объясненную и
случайную.
Задача моделирования формулируется следующим образом:
на основании экспериментальных данных определить объясненную часть и,
рассматривая случайную составляющую как случайную величину, получить
(возможно, после некоторых предположений) оценки параметров ее
распределения.
Таким образом, эконометрическая модель имеет следующий вид: Y=f(x)+e
Наблюдаемое
значение зависимой
переменной Y
=
Объясненная часть,
зависящая от значений
объясняющих
переменных f(x)
+
Случайная
составляющая e

9.

Предположим,
получено следующее выражение для объясненной части переменной Y — цены
автомобиля:
y =18000 −1000x1 − 0,5x2,
Где: y — ожидаемая цена автомобиля (в усл. ден. ед., здесь и далее у.е.);
Х1 — срок эксплуатации автомобиля (в годах);
Х2 — пробег (в тыс. км)1.
Полученная модель позволяет понять: как именно формируется рассматриваемая
экономическая переменная — цена на автомобиль. Она дает возможность выявить
влияние каждой из объясняющих переменных на цену автомобиля
(так, в данном случае цена нового автомобиля (при x1=0, x2=0) 18000 у.е., при этом
только за счет увеличения срока эксплуатации на 1 год цена автомобиля уменьшается в
среднем на 1000 у.е., а только за счет увеличения пробега на 1 тыс. км — на 0,5 у.е.).
И что наиболее важно, полученная модель позволяет п р о г н о з и р о в а т ь цену
на автомобиль.
Менеджер автосалона может определить ожидаемую цену вновь поступившего для
продажи автомобиля, даже если его год выпуска и пробег не встречались ранее в
данном салоне.

10.

Если имеются статистические данные, характеризующие
моделируемый экономический объект в данный и
предшествующие моменты времени, то для верификации
(проверки, подтверждения) модели, построенной для прогноза,
достаточно сравнить реальные значения переменных в
последующие моменты времени с соответствующими их
значениями, полученными на основе рассматриваемой модели
по данным предшествующих моментов.

11.

2. Этапы эконометрического моделирования
Можно выделить шесть основных этапов эконометрического
моделирования:
-постановочный,
-априорный,
-этап параметризации,
-информационный,
-этапы идентификации и
-верификации модели.
1-й этап (постановочный). Формируется цель исследования, набор
участвующих в модели экономических переменных.
В качестве цели эконометрического моделирования обычно
рассматривают анализ исследуемого экономического объекта (процесса);
прогноз его экономических показателей, имитацию развития объекта при
различных значениях экзогенных переменных (отражая их случайный
характер, изменение во времени), выработку управленческих решений.

12.

При выборе экономических переменных необходимо теоретическое
обоснование каждой переменной.
Рекомендуется, чтобы число переменных было не очень большим и, как
минимум, в несколько раз меньше числа наблюдений.
Объясняющие переменные не должны быть связаны функциональной или
тесной корреляционной зависимостью, так как это может привести к
невозможности оценки параметров модели или к получению неустойчивых, не
имеющим реального смысла оценок, т. е. к явлению мультиколлинеарности.
Для отбора переменных могут быть использованы различные методы, в
частности процедуры пошагового отбора переменных.
Для оценки влияния качественных признаков (например, пол, образование и
т. п.) могут быть использованы фиктивные переменные.
Но в любом случае определяющим при включении в модель тех или иных
переменных является экономический (качественный) анализ
исследуемого объекта.

13.

2-й этап (априорный). Проводится анализ сущности изучаемого объекта,
формирование и формализация априорной (известной до начала моделирования)
информации.
3-й этап (параметризация). Осуществляется непосредственно моделирование, т.е.
выбор общего вида модели, выявление входящих в нее связей.
Основная задача на этом этапе, — выбор вида функции f (X) в эконометрической
модели, в частности, возможность использования линейной модели как наиболее
простой и надежной.
Важной проблемой на этом (и предыдущих) этапе эконометрического
моделирования является проблема спецификации модели, в частности:
- выражение в математической форме обнаруженных связей и соотношений;
- установление состава экзогенных и эндогенных переменных, в том числе лаговых;
- формулировка исходных предпосылок и ограничений модели.
От того, насколько удачно решена проблема спецификации модели, в значительной
степени зависит успех всего эконометрического моделирования.

14.

4-й этап (информационный). Осуществляется сбор необходимой
статистической информации — наблюдаемых значений экономических
переменных
(xi1, xi2,…,xip; yi1,yi2,…,yiq), i = 1,…, n.
Здесь могут быть наблюдения, полученные как с участием исследователя,
так и без его участия (в условиях активного или пассивного эксперимента).
5-й этап (идентификация модели). Осуществляется статистический
анализ модели и оценка ее параметров. (Очень важный и трудоемкий этап!).
С проблемой идентификации модели не следует путать проблему ее
идентифицируемости, (т. е. проблему возможности получения однозначно
определенных параметров модели, заданной системой одновременных
уравнений (точнее, параметров структурной формы модели, раскрывающей
механизм формирования значений эндогенных переменных, по параметрам
приведенной формы модели, в которой эндогенные переменные
непосредственно выражаются через предопределенные переменные).

15.

6-й этап (верификация модели). Проводится проверка истинности,
адекватности модели.
Выясняется:
- насколько удачно решены проблемы спецификации, идентификации и
идентифицируемости модели,
- какова точность расчетов по данной модели,
- насколько соответствует построенная модель моделируемому реальному
экономическому объекту или процессу.
Следует заметить, что если имеются статистические данные,
характеризующие моделируемый экономический объект в данный и
предшествующие моменты времени, то для верификации модели,
построенной для прогноза, достаточно сравнить реальные значения
переменных в последующие моменты времени с соответствующими их
значениями, полученными на основе рассматриваемой модели по данным
предшествующих моментов.

16.

Разделение эконометрического моделирования на отдельные этапы
носит в известной степени условный характер, так как эти этапы могут
пересекаться, взаимно дополнять друг друга и т. п.
Основные разделы эконометрики:
•классическая и обобщенная модели регрессии,
•временные ряды
•системы одновременных уравнений,
•модели с различными типами выборочных данных.

17.

3. Виды зависимости между случайными
величинами
Функциональная, статистическая и корреляционная
зависимости
В естественных науках часто речь идет о функциональной зависимости
(связи) между переменными величинами, когда каждому значению одной
переменной соответствует вполне определенное значение другой (например,
скорость свободного падения в вакууме в зависимости от времени и т.д.)
В экономике в большинстве случаев между переменными величинами
существуют зависимости, когда каждому значению одной переменной
соответствует не какое-то определенное, а м н о ж е с т в о возможных
значений другой переменной.
Иначе говоря, каждому значению одной переменной соответствует
определенное (условное) распределение другой переменной. Такая

18.

Возникновение понятия статистической связи обуславливается тем,
что зависимая переменная подвержена влиянию ряда неконтролируемых или
неучтенных факторов, а также тем, что измерение значений переменных
неизбежно сопровождается некоторыми случайными ошибками.
Примером статистической связи является зависимость урожайности от
количества внесенных удобрений, производительности труда на предприятии
от его энерговооруженности и т.п.
Если зависимость между двумя переменными такова, что каждому
значению одной переменной соответствует определенное условное
математическое ожидание (среднее значение) другой, то такая статистическая
зависимость называется корреляционной.
Иначе, корреляционной зависимостью между двумя переменными
называется функциональная зависимость между значениями одной из
них и условным математическим ожиданием другой.

19.

Таким образом, зависимость между случайными величинами может быть следующих
видов:
• функциональная: если значению случайной величины x по определенному
закону ставится в соответствие значение случайной величины y;
• статистическая (вероятностная): если значению случайной величины x ставится в
соответствие определенное распределение случайной величины y.
Статистическая зависимость, в которой при изменении случайной величины x
изменяется условное математическое ожидание случайной величины Y , называется
корреляционной зависимостью.
Если условное математическое ожидание случайной величины Y не изменяется при
изменении значений X, то корреляционной зависимости нет.
Средние величины результативного признака изменяются под влиянием изменения
многих факторных признаков. Некоторые из них могут быть и неизвестны.

20.

Пример: Себестоимость продукции зависит от производительности труда:
чем выше производительность труда, тем ниже себестоимость.
Себестоимость зависит также от ряда других факторов.
Поэтому нельзя утверждать, что при повышении производительности труда
на 10% себестоимость снизится также на 10%.
(Может случиться, что себестоимость даже повысится!)

21.

Основным аппаратом эконометрики является раздел математической статистики корреляционно-регрессионный анализ.
Задача корреляционного анализа – выявление характера и степени взаимосвязи
между экономическими показателями, являющимися случайными величинами,
выявление того, насколько изменение одной экономической переменной (фактора) в
среднем влияет на изменение другой экономической переменной (результативного
признака).
В корреляционном анализе определяется показатель, характеризующий степень
тесноты взаимосвязи экономических показателей.
В регрессионном анализе строится модель регрессии в виде математической
функции, которая показывает влияние факторов на некоторый экономический
показатель.
Теоретически корреляция и регрессия связаны между собой.

22.

Функция, которая описывает закон изменения условного математического
ожидания случайной величины Y при изменении другой случайной
величины X, называется функцией регрессии Y на X.
Если двумерная случайная величина (X, Y ) распределена по
нормальному закону, то функция регрессии линейная, корреляционная
зависимость тоже линейная.
Практическая интерпретация корреляционного и регрессионного анализа выводы исследования можно интерпретировать лишь как некоторые
усредненные свойства, обобщенные характеристики экономических
процессов.

23.

Задачи регрессионного анализа:
-установление формы зависимости между переменными,
-оценка функции регрессии,
-оценка неизвестных значений (прогноз значений) зависимой переменной.
В регрессионном анализе рассматриваются односторонняя зависимость случайной
переменной Y от одной (или нескольких) неслучайной независимой переменной Х.
Такая зависимость может возникнуть в случае, когда при каждом фиксированном
значении Х соответствующие значения Y подвержены случайному разбросу за счет
действия ряда неконтролируемых факторов.
Зависимость Y от Х (ее называют регрессионной) может быть представлена в виде
модельного уравнения регрессии Y по Х.
При этом:
- зависимую переменную Y называют также функцией отклика, объясняемой,
выходной, результирующей, эндогенной переменной, результативным
признаком,
- независимую переменную X — объясняющей, входной, предсказывающей,
предикторной, экзогенной переменной, фактором, регрессором, факторным
признаком.

24.

Для точного описания уравнения регрессии необходимо знать условный
закон распределения зависимой переменной Y при условии, что переменная Х
примет значение х, т. е. Х=х.
В статистической практике такую информацию получить, как правило, не
удается, так как обычно исследователь располагает лишь выборкой пар
значений (хi, yi) ограниченного объема n. В этом случае речь может идти об
оценке (приближенном выражении, аппроксимации) по выборке функции
регрессии. Такой оценкой является выборочная линия (кривая) регрессии.
Допустим, у нас есть данные про две переменные, и требуется численно
оценить, как одна переменная зависит от другой.
Для удобства введем следующие обозначения:
x — объясняющая переменная (независимая переменная или регрессор),
y — объясняемая переменная (зависимая),
n — количество наблюдений, которое имеется в нашем распоряжении
(размер выборки).

25.

Например,
x — площадь однокомнатной квартиры (в квадратных метрах),
y — цена квартиры (в миллионах рублей).
Понятно, что большие квартиры в среднем стоят дороже, чем
маленькие, однако было бы ценно получить конкретное уравнение,
которое описывает эту зависимость.
Другой пример:
x — образование индивида (число лет обучения),
y — его ежегодный доход (в рублях).
Есть гипотеза, что более образованные индивиды в среднем
зарабатывают больше, чем менее образованные, и интересно было
бы выяснить, действительно ли это так, и если да, то какую
прибавку к доходу дает один дополнительный год обучения.
Тогда формально нашу задачу можно записать так: имеется
выборка из n пар наблюдений (xi,yi),i=1,…,n, требуется подобрать
функцию, которая наилучшим образом описывает зависимость
переменной y от переменной x.

26.

Для начала предположим, что искомая функция является линейной.
Если каждой паре наблюдений (xi,yi) поставить в соответствие точку на плоскости, то
получится рисунок:
Диаграмма рассеяния (поле корреляции)

27.

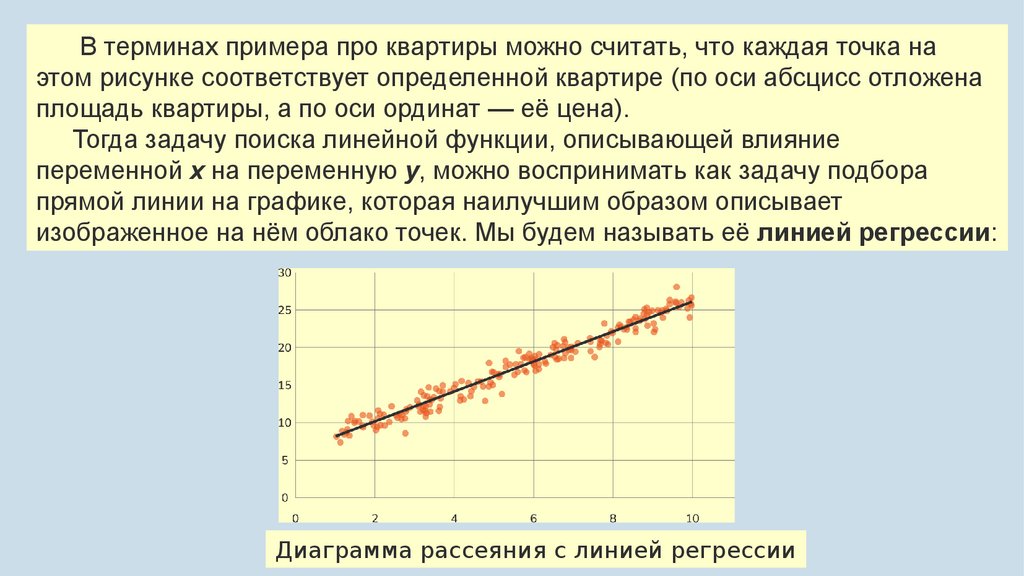
В терминах примера про квартиры можно считать, что каждая точка на
этом рисунке соответствует определенной квартире (по оси абсцисс отложена
площадь квартиры, а по оси ординат — её цена).
Тогда задачу поиска линейной функции, описывающей влияние
переменной x на переменную y, можно воспринимать как задачу подбора
прямой линии на графике, которая наилучшим образом описывает
изображенное на нём облако точек. Мы будем называть её линией регрессии:
Диаграмма рассеяния с линией регрессии

28.

По расположению эмпирических точек можно предполагать
наличие л и н е й н о й корреляционной (регрессионной)
зависимости между переменными Х и Y.
Поэтому уравнение регрессии будем искать в виде
линейного уравнения:
Y(с крышкой) = b0 + b1 x

29.

Чтобы получить уравнение прямой, нам нужно подобрать численные
значения двух коэффициентов: свободного члена, который мы обозначим b0^, и
коэффициента наклона b1^. Тогда нашу линию регрессии можно записать так:
y^i =b0^ + b1^ xi
Здесь y^i — предсказываемое уравнением регрессии значение
переменной y.
Поскольку линия регрессии лишь приближенно описывает облако точек,
предсказанное значение y^i может не совпадать с фактическим
значением yi (то есть с тем значением, которое действительно наблюдается в
данных).
Отклонения предсказанных значений от фактических будем называть
остатками регрессии и обозначать ei=yi−y^i.
Геометрически остатки регрессии характеризуют отклонение
соответствующих наблюдений от линии регрессии по вертикали.
Положительным остаткам соответствует отклонение вверх, а отрицательным —
вниз.

30.

Важно подчеркнуть различие между параметрами уравнения без
«крышек» в выражении yi=b0+b1xi+εi, и их оценками bk c
«крышками».
Это различие состоит в том, что параметры xi и yi — это некоторые
истинные значения параметров модели, которые на практике
никогда не известны исследователю.
Все, что исследователь в силах сделать — собрать данные и эти
значения оценить приближенно, — это оценки истинных значений,
которые получает исследователь, используя выборочные данные.
Так как и b0^ и b1^ рассчитываются на основе случайной выборки,
то они являются случайными величинами.
Требуется найти формулы для расчета неизвестных параметров b0
и b1 уравнения линейной регрессии.
Согласно методу наименьших квадратов неизвестные
параметры b0 и b1 выбираются таким образом, чтобы сумма квадратов
отклонений эмпирических значений yi от значений yi , найденных по

31.

Естественно подбирать уравнение таким образом, чтобы отклонения
предсказаний от фактических значений были не слишком большими, то есть
чтобы остатки ei были маленькими. На первый взгляд кажется, что хорошей
идеей в этом случае будет идея подбирать b0^ и b1^ таким образом, чтобы
сумма остатков e1+e2+…+en была как можно ближе к нулю.
Обычно вместо простой суммы остатков минимизируют сумму квадратов
остатков, то есть решают такую задачу:
Такой метод поиска интересующих нас величин b0^ и b1^ называется
методом наименьших квадратов (МНК).

32.

Согласно методу наименьших квадратов неизвестные параметры b0 и b1
выбираются таким образом, чтобы сумма квадратов отклонений
эмпирических значений yi от значений, найденных по уравнению регрессии,
была минимальной.
Для оценки параметров b0 и b1 возможны и другие подходы. Так,
например, согласно методу наименьших модулей следует минимизировать
сумму абсолютных величин отклонений.
Однако метод наименьших квадратов существенно проще при
проведении вычислительной процедуры и дает хорошие по статистическим
свойствам оценки.

33.

Пример: По данным таблицы найти уравнение регрессии Y по Х.
Таблица
i
1 ●2 ●3 ●4 ●5 ●6 ●7
● x
i
8 ● 11 ● 12 ● 9
8
8
9
yi
5
10
10
7
5
6
6
8
9
5
9
8
6
10
12
8
Р е ш е н и е. Вычислим все необходимые суммы:
Сумма xi = 8+11+12+9+8+8+9+9+8+12=94;.
Сумма x2 = 82+112+122+92+82+82+92+92+82+122=908;
Сумма yi = 5+10+10+7+5+6+6+5+6+8=68;
Сумма xi yi = 8•5+11•10+12•10+9•7+8•5+8•6+9•6+
+9•5+8•6+12•8 = 664.
Затем по формулам находим выборочные характеристики и параметры уравнений регрессии.

34.

5. Предпосылки классической линейной модели парной регрессии
Желательно, чтобы найденные оценки были близки к истинным значениям
оцениваемых параметров. Поэтому важно знать: при каких условиях можно
доверять этим оценкам, то есть рассчитывать на то, что полученное
уравнение регрессии будет близко к истине. Эти условия называют
предпосылками классической линейной модели парной регрессии.
Предпосылки классической линейной модели парной
регрессии (КЛМПР):
1.
2. В модели .22) возмущение (или зависимая переменная yi) есть величина
случайная, а объясняющая переменная xi — величина неслучайная.
Модель линейна по параметрам и корректно специфицирована
yi=b0+b2xi+εi, i=1,2,…,n.
x1,x2,…,xn — детерминированные (неслучайные) величины, не все
одинаковые.

35.

2. Математическое ожидание случайных ошибок равно нулю Eεi=0.
1.
3. Дисперсия случайной ошибки одинакова для всех наблюдений, постоянна
для любого i var(εi)=S2.
2.
4. Случайные ошибки, относящиеся к разным наблюдениям, не
коррелированы взаимно независимы.
3.
5. Случайные ошибки имеют нормальное распределение εiN (0,S2).

36.

Первая предпосылка (Модель линейна по параметрам и корректно
специфицирована yi=b0+b1xi+εi, i=1,2,…,n):
правильная спецификация подразумевает в первую очередь отсутствие
среди прочих факторов других переменных, которые одновременно влияют
на y и коррелируют с x. Нарушение этого требования приводит к серьезным
проблемам при верификации модели.
Предпосылка №1 (x1,x2,…,xn — детерминированные
(неслучайные) величины, не все одинаковые) касается двух важных
аспектов.
Во-первых, мы предполагаем, что регрессоры xi являются неслучайными
величинами. Это техническое предположение, которое упрощает некоторые
выкладки в расчетах. Следует обратить внимание, что εi в отличие от
регрессоров являются случайными величинами, а следовательно, и yi тоже
случайны, так как представляют собой сумму неслучайной
компоненты b1+b2xi и случайной величины εi.
Во-вторых, в рамках предпосылки №2 мы предполагаем, что не все

37.

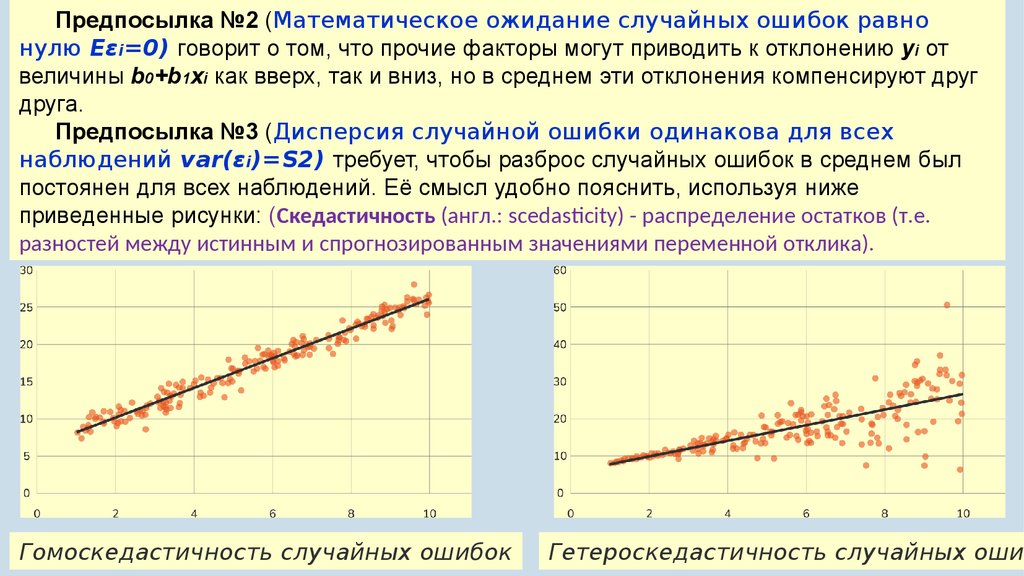
Предпосылка №2 (Математическое ожидание случайных ошибок равно
нулю Eεi=0) говорит о том, что прочие факторы могут приводить к отклонению yi от
величины b0+b1xi как вверх, так и вниз, но в среднем эти отклонения компенсируют друг
друга.
Предпосылка №3 (Дисперсия случайной ошибки одинакова для всех
наблюдений var(εi)=S2) требует, чтобы разброс случайных ошибок в среднем был
постоянен для всех наблюдений. Её смысл удобно пояснить, используя ниже
приведенные рисунки: (Скедастичность (англ.: scedasticity) - распределение остатков (т.е.
разностей между истинным и спрогнозированным значениями переменной отклика).
Гомоскедастичность случайных ошибок
Гетероскедастичность случайных оши

38.

В первом случае предпосылка о постоянстве дисперсии случайной ошибки
выполнена, а во втором — нет, так как разброс точек вокруг линии регрессии
растет по мере увеличения объясняющей переменной, следовательно, можно
заключить, что дисперсия случайной ошибки не является одинаковой для
всех наблюдений.
Ситуация, когда предпосылка №3 выполнена (то есть ситуация,
соответствующая первому рисунку) называется гомоскедастичностью
случайных ошибок.
Альтернативная ситуация называется гетероскедастичностью
случайных ошибок.

39.

Из предпосылки №4 (Случайные ошибки, относящиеся к разным
наблюдениям, взаимно независимы) следует, что случайные ошибки,
относящиеся к разным наблюдениям, не коррелированы друг с
другом: cov(εi,εj)=0 при i≠j.
Предпосылка №5 (Случайные ошибки имеют нормальное
распределение εiN(0,S2)) не требуется для обеспечения хороших
свойств оценок коэффициентов (следует обратить внимание, что, в
формулировке теоремы Гаусса — Маркова, которая приведена ниже, она не
фигурирует), однако будет полезна для тестирования гипотез и построения
доверительных интервалов.

40.

Теорема Гаусса — Маркова: Если выполнены предпосылки 1-4
классической линейной модели парной регрессии, то МНК-оценки
коэффициентов b0^ и b1^ будут:
(а) несмещенными,
(б) эффективными в классе всех несмещенных и линейных по y оценок.
Оценка называется несмещенной, если её математическое ожидание
совпадает с истинным значением оцениваемого параметра: Eb1^=b1.
Свойство эффективности означает, что оценка характеризуется
минимальной дисперсией среди всех альтернативных оценок в данном классе,
то есть является «наиболее точной» оценкой интересующего нас параметра.
Линейность по y означает, что мы рассматриваем все оценки, которые могут
быть представлены в виде линейной комбинации значений объясняемой
переменной.

41.

Если переформулировать свойства несмещенности и эффективности
нестрого, то можно сказать, что при выполнении предпосылок 1-4
МНК-оценки параметров окажутся хорошими: они будут «в среднем
правильными» и наиболее точными.
Теорема Гаусса — Маркова дает важную мотивацию для того, чтобы
оценивать параметры модели именно методом наименьших
квадратов, а не каким-то альтернативным способом.
Несмещенность и эффективность — это свойства оценок при
фиксированном объеме выборки (при фиксированном n). Во многих случаях
удобно также использовать асимптотические свойства оценок, то есть
свойства, которые имеют место при n→∞ (например, состоятельность).

42.

Спасибо за внимание!