Способы решения задач с параметрами

1. Исследовательская работа на тему:

«Способы решения
задач с параметрами»

2. Актуальность:  Тема моей исследовательской работы наиболее актуальна , так как затрагивает современную проблему, знакомую

Актуальность:
Тема моей исследовательской работы наиболее актуальна , так
как затрагивает современную проблему, знакомую каждому
выпускнику, а именно – высокорезультативное решение задач
Единого Государственного Экзамена.
Задачи с параметрами традиционно - это одна из самых трудных
тем ЕГЭ. Поэтому уже сейчас, учась в 10 классе, пока « не
поджимает время», надо приложить максимум стараний, чтобы
разобраться в способах решения этих трудных, но в то же время,
красивых задач.

3. Цель работы: Научиться решать задачи с параметрами наиболее легкими способами Задачи: 1. Найти и изучить литературу по теме

исследования.
2. Разобраться, что такое параметр и задачи с
параметром
3. Исследовать разновидности задач с параметрами
4. Исследовать способы решения задач с параметрами
и выбрать из них для себя 2 самых лёгких
5. Потренироваться в решении задач с параметрами
выбранными способами

4. Гипотеза: Убедиться , что метод мажорант и графический метод- самые лёгкие методы решения Объект исследования: Задачи с

параметрами
Предмет исследования:
параметрами
Способы решения задач с
Методы работы:
1. Исследовательский ( изучение литературы)
2. Эксперимент (исследование изменения вида кривой, в
зависимости от параметров входящих в её уравнение)

5. При подготовке данного материала я прочитала большое количество тематических книг, в которых описывались различные способы их

решения: аналитический, графический, метод,
симметрии, метод областей, метод мажорант, метод ,
использующий производную.
В ходе исследования я поняла, что наиболее лёгкими и
наглядными для меня оказались графический способ и способ
мажорант .

6. Что такое параметр? Параметром называется независимая переменная, значение которой в задаче считается заданным числом

7. Основные типы задач с параметрами? Тип 1.  Уравнения, неравенства, их системы и совокупности, которые необходимо решить

Основные типы задач с
параметрами?
Тип 1.
Уравнения, неравенства, их
системы и совокупности,
которые необходимо решить

8. Основные типы задач с параметрами? Тип 2.  Уравнения, неравенства, их системы и совокупности, для которых требуется определить

Основные типы задач с
параметрами?
Тип 2.
Уравнения, неравенства, их
системы и совокупности, для
которых требуется
определить количество решений

9. Основные типы задач с параметрами? Тип 3.  Уравнения, неравенства, их системы и совокупности, для которых требуется найти все

Основные типы задач с
параметрами?
Тип 3.
Уравнения, неравенства, их системы и совокупности,
для которых требуется найти все те значения
параметра, при которых указанные уравнения,
неравенства, их системы и совокупности
имеют заданное число решений
(в частности, не имеют или имеют бесконечное
множество решений).

10. Основные типы задач с параметрами? Тип 4. 

Основные типы задач с
параметрами?
Тип 4.
Уравнения, неравенства, их системы и
совокупности, для которых при искомых
значениях параметра
множество решений
удовлетворяет заданным условиям
в области определения.

11.

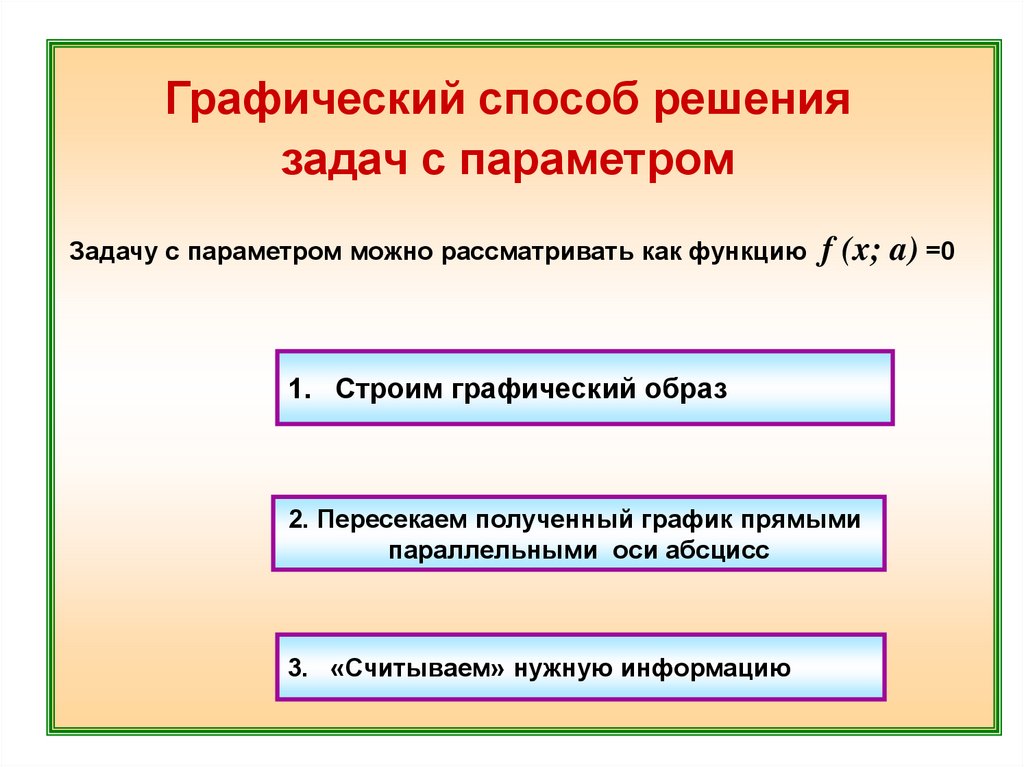
Графический способ решения
задач с параметром
Задачу с параметром можно рассматривать как функцию
f (x; a) =0
1. Строим графический образ
2. Пересекаем полученный график прямыми
параллельными оси абсцисс
3. «Считываем» нужную информацию

12.

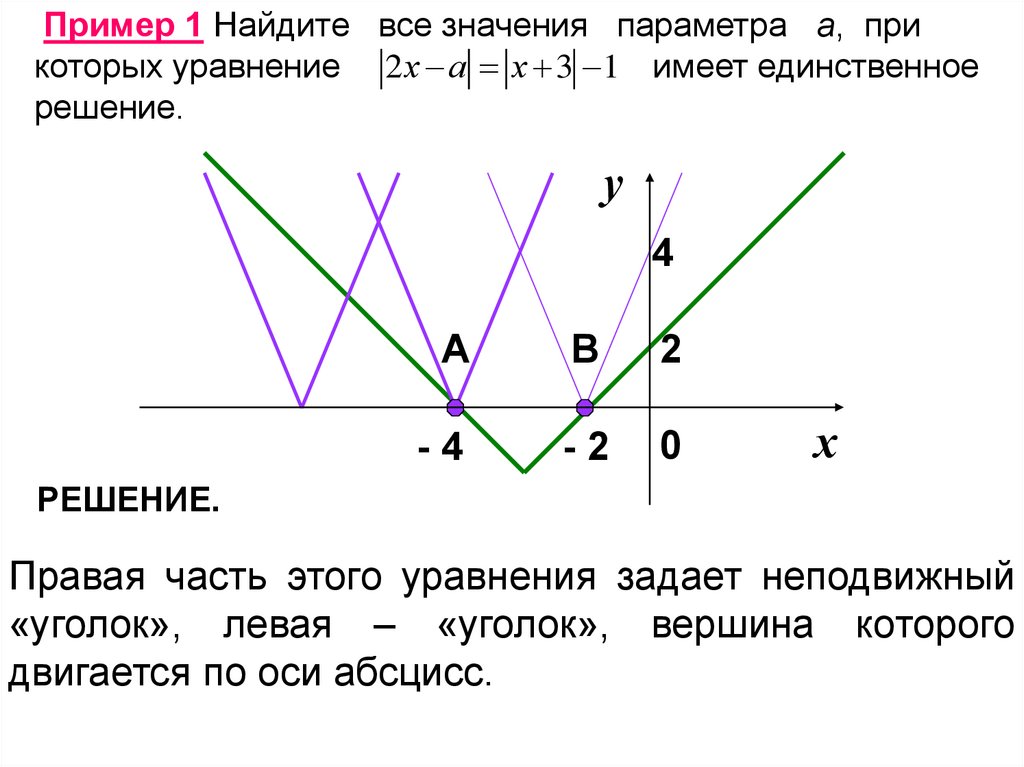
Пример 1 Найдите все значения параметра а, при
которых уравнение 2 х а х 3 1 имеет единственное
решение.
у
4
А
В
2
-4
-2
0
х
РЕШЕНИЕ.
Правая часть этого уравнения задает неподвижный
«уголок», левая – «уголок», вершина которого
двигается по оси абсцисс.

13.

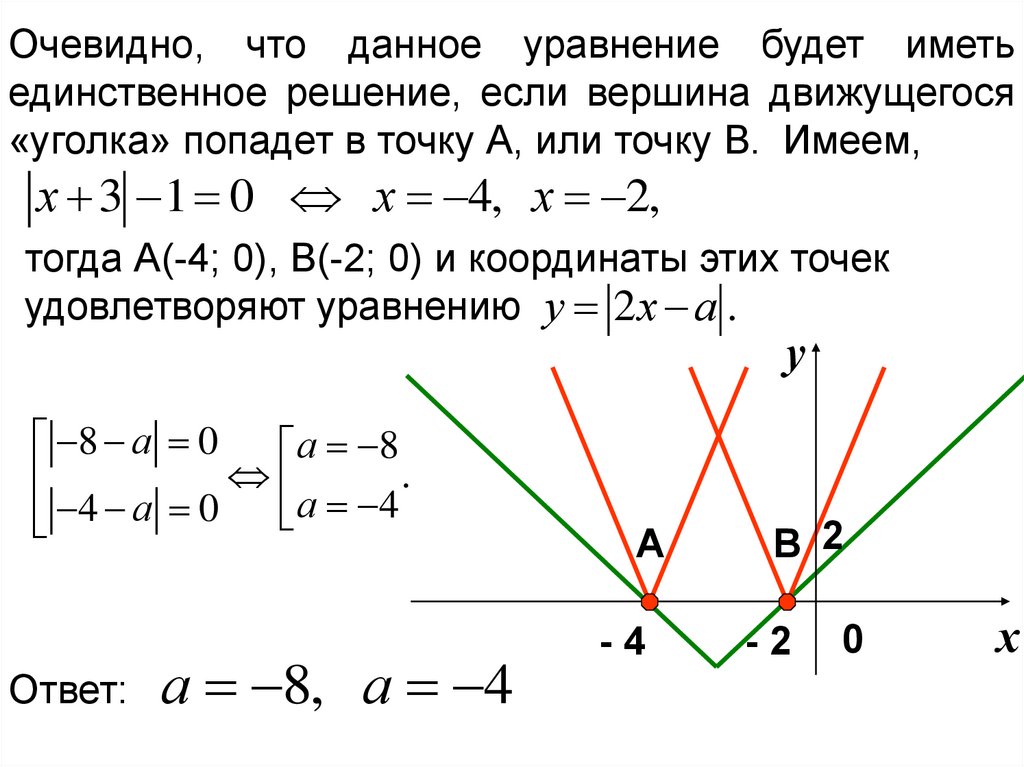
Очевидно, что данное уравнение будет иметь
единственное решение, если вершина движущегося
«уголка» попадет в точку А, или точку В. Имеем,
х 3 1 0 х 4, х 2,
тогда А(-4; 0), В(-2; 0) и координаты этих точек
удовлетворяют уравнению у 2 х а .
у
8 а 0
а 8
.
а 4
4 а 0
Ответ:
а 8, а 4
А
-4
В 2
-2
0
х

14.

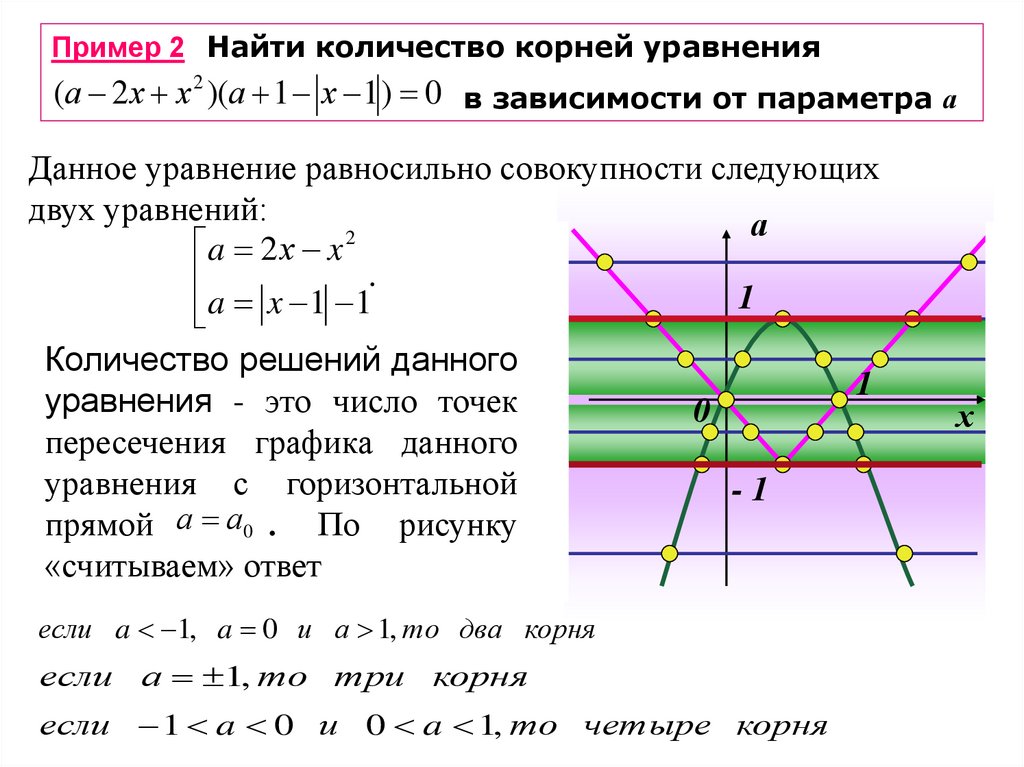
Пример 2 Найти количество корней уравнения
(а 2 х х 2 )(а 1 х 1 ) 0 в зависимости от параметра а
Данное уравнение равносильно совокупности следующих
двух уравнений:
а
2
a 2 х x
.
1
a x 1 1
Количество решений данного
1
уравнения - это число точек
0
пересечения графика данного
уравнения с горизонтальной
-1
прямой а а0 . По рисунку
«считываем» ответ
если a 1, a 0 и а 1, то два корня
если а 1, то три корня
если 1 a 0 и 0 a 1, то четыре корня
х

15.

х у а ,
2 у 2 1
х
Пример 3. Сколько решений имеет система
в зависимости от параметра а?
решений нет при
y
a 1
Графикомпри
первого
4 решения
а=1
уравнения является
8 решений
при
1 a с2
семейство
квадратов
вершинами
4 решения
прив точках
а 2
а;0 , 0; а , а;0 , 0; а
решений нет при a 2 -2
Графиком второго
решений нет, если
Ответ:
уравнения является
a 1 или a 2
неподвижная окружность с
4 решения,
центром
в начале если
а 1и радиусом
или а 12
координат
8 решений, если
1 a 2
2
2
1
a
2
a
a
0
a
-1
2
-2
x
1
2
2

16.

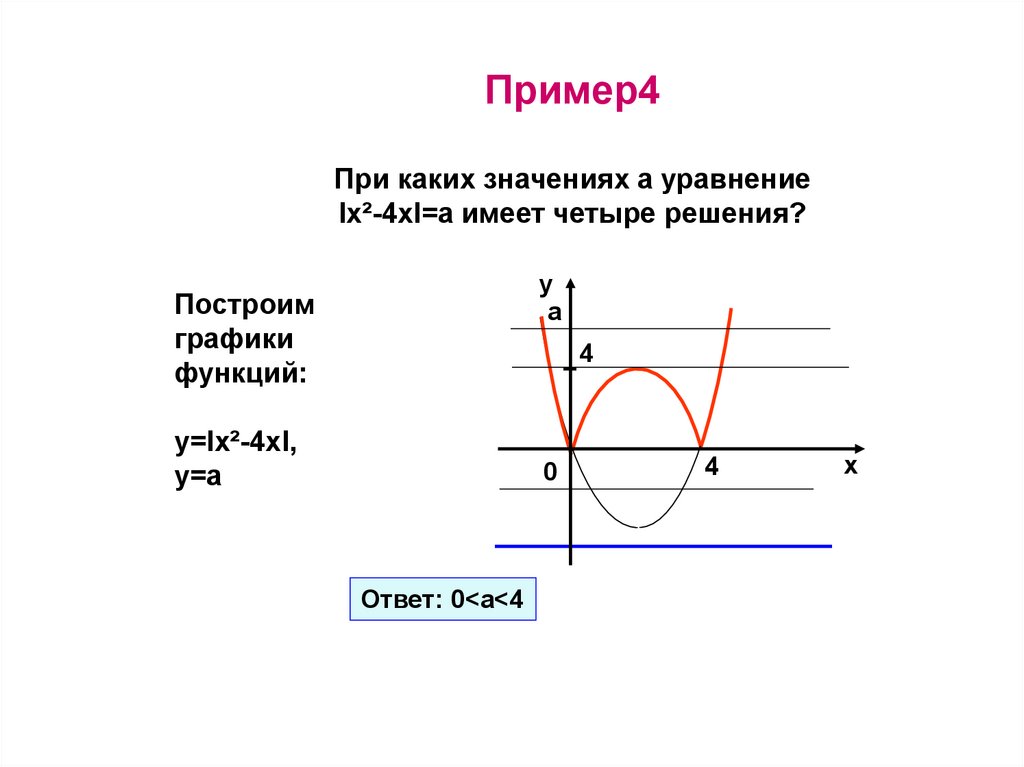
Пример4
При каких значениях а уравнение
lх²-4хl=а имеет четыре решения?
у
а
Построим
графики
функций:
4
у=lх²-4хl,
у=а
0
Ответ: 0<а<4
4
х

17.

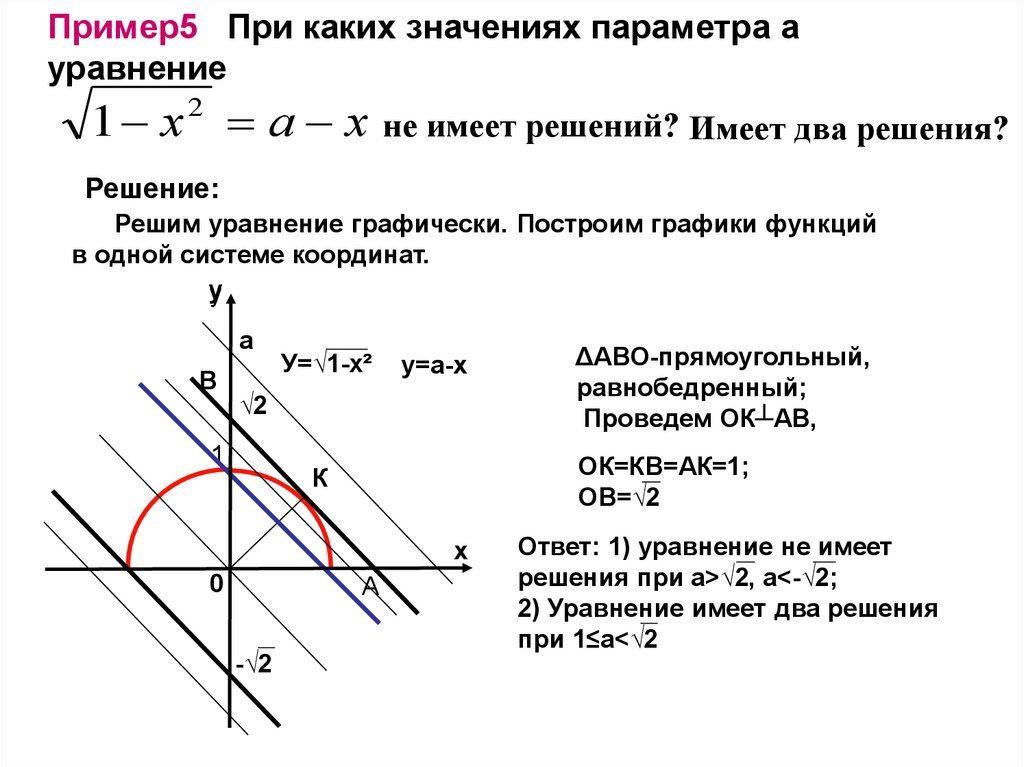
Пример5 При каких значениях параметра а
уравнение
1 х а х
2
не имеет решений? Имеет два решения?
Решение:
Решим уравнение графически. Построим графики функций
в одной системе координат.
у
а
В
У=√1-х²
у=а-х
√2
1
ОК=КВ=АК=1;
ОВ=√2
К
х
А
0
-√2
ΔАВО-прямоугольный,
равнобедренный;
Проведем ОК┴АВ,
Ответ: 1) уравнение не имеет
решения при а>√2, а<-√2;
2) Уравнение имеет два решения
при 1≤а<√2

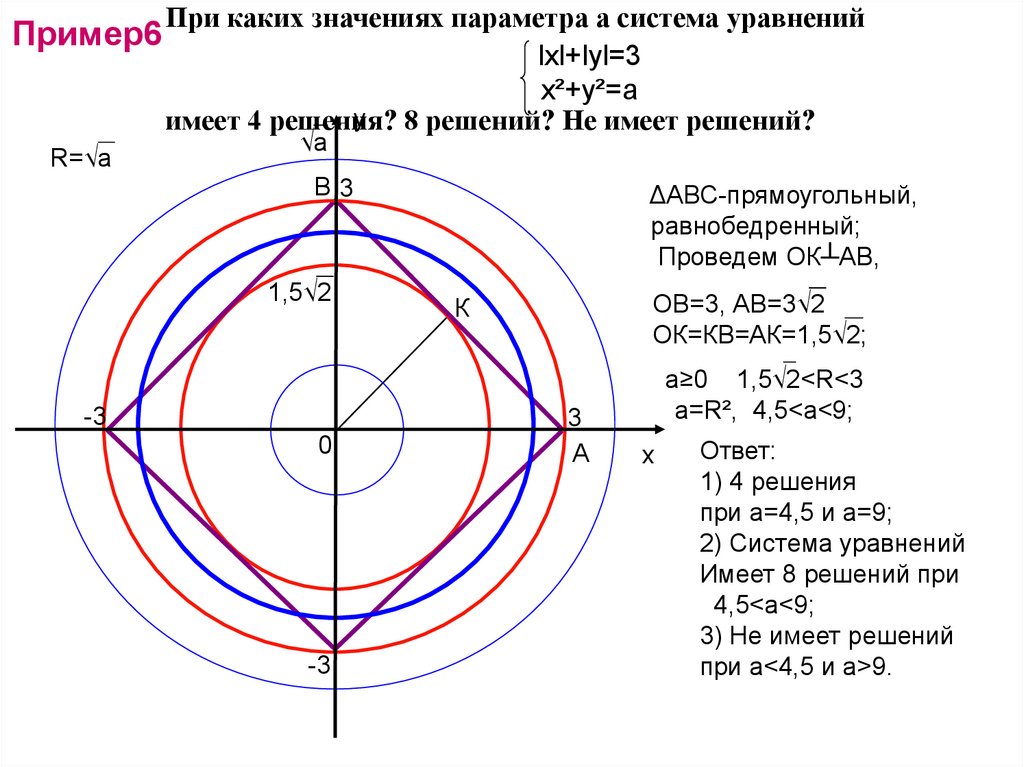
18. При каких значениях параметра а система уравнений имеет 4 решения? 8 решений? Не имеет решений?

При каких значениях параметра а система уравнений
Пример6
lхl+lуl=3
х²+у²=а
у 8 решений? Не имеет решений?
имеет 4 решения?
R=√а
√а
В3
1,5√2
-3
0
-3
ΔАВС-прямоугольный,
равнобедренный;
Проведем ОК┴АВ,
ОВ=3, АВ=3√2
ОК=КВ=АК=1,5√2;
К
3
А
а≥0 1,5√2<R<3
а=R², 4,5<a<9;
х
Ответ:
1) 4 решения
при а=4,5 и а=9;
2) Система уравнений
Имеет 8 решений при
4,5<a<9;
3) Не имеет решений
при а<4,5 и а>9.

19.

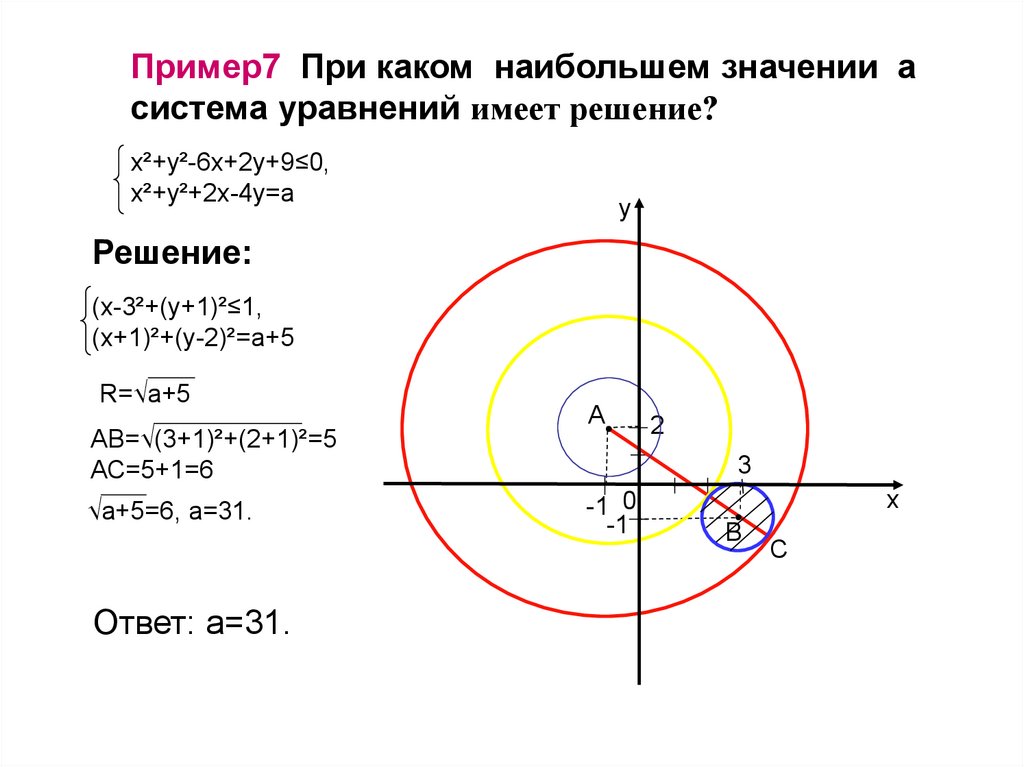
Пример7 При каком наибольшем значении а
система уравнений имеет решение?
х²+у²-6х+2у+9≤0,
х²+у²+2х-4у=а
у
Решение:
(х-3²+(у+1)²≤1,
(х+1)²+(у-2)²=а+5
R=√а+5
АВ=√(3+1)²+(2+1)²=5
АС=5+1=6
√а+5=6, а=31.
Ответ: а=31.
А
2
3
-1 0
-1
х
В
С

20.

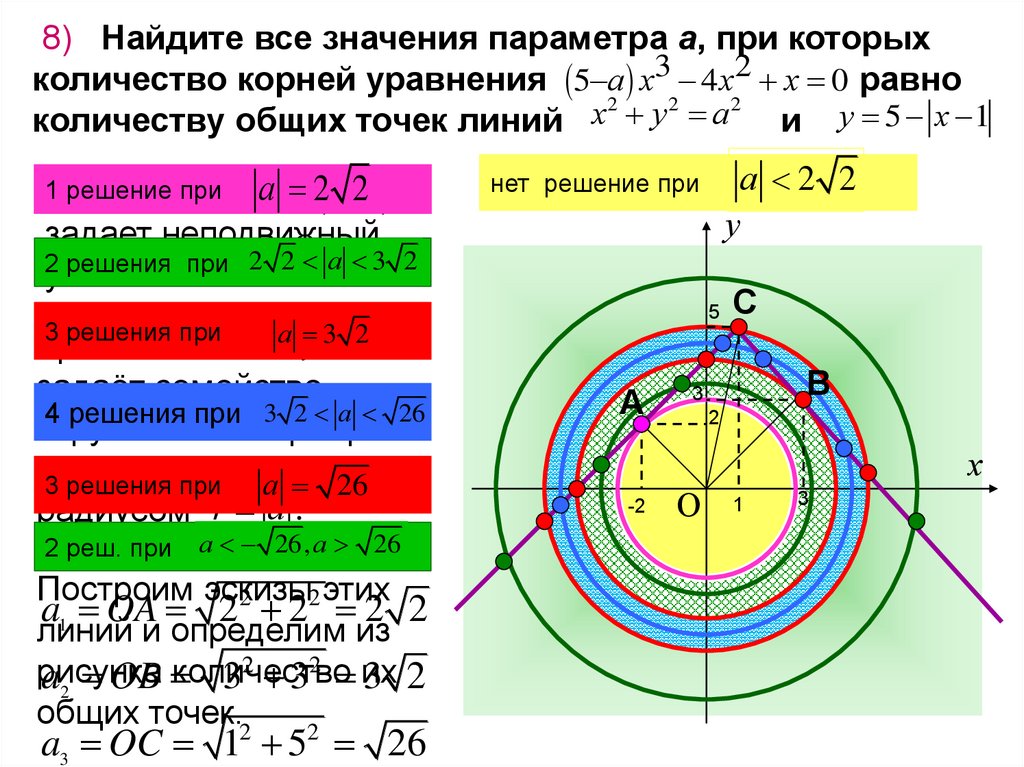
8) Найдите все значения параметра а, при которых
количество корней уравнения 5 а х3 4 х2 х 0 равно
2
2
2
х
у
а
количеству общих точек линий
и у 5 х 1
1
решение при
Уравнение
а 5 2х 21
у
задает неподвижный
2 решения при 2 2 а 3
уголок.
у
2
3 решения при
а
х
у 3 2а
Уравнение
задаёт семейство
4 решения при 3 2 а 26
окружностей
с центром
в3 начале
координат
решения при
а 26и
радиусом r а .
2
2 реш. при
2
а 2 2
нет решение при
5
С
2
а 26, a 26
Построим эскизы
2
2 этих
a1 OA 2 2 2 2
линий
и определим из
рисунка
количество
a2 OB
32 32 их
3 2
общих точек.2
2
a3 OC 1 5 26
А
В
3
2
х
-2
О
1
3

21.

Запишем первое уравнение в виде х 5 а х 2 4 х 1 0
Заметим, что х = 0 – корень не зависимо от параметра а.
Уравнение 5 а х2 4 х 1 0 может иметь 0, 1 или 2 решения
в зависимости от параметра а и дискриминанта D 4 a. 1
одно решение Два решения
первое
уравнение
совокупность
линий
a 1
а = 5; а = 1
Три решения
a 1
а 2 2
3 2 a 2 2, а 3 2, а 26
а 2 2
2 2 a 3 2,
а 3 2,
а 26, a 26
а 26
Осталось заметить, что условие задачи выполняется только
в трех точках при а 2 2, а 3 2 и a 26
Ответ: а 2 2, а 3 2 и a 26

22.

Задачи,
взятые из материалов ЕГЭ
прошлых лет

23.

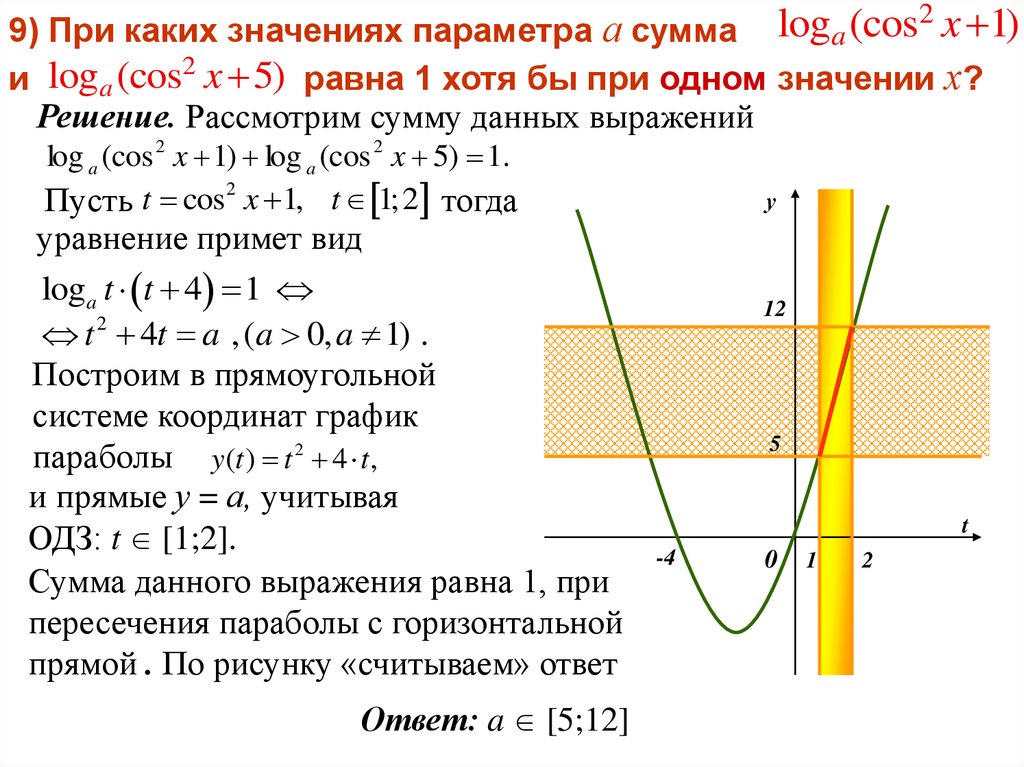
9) При каких значениях параметра а сумма loga (cos x 1)
и loga (cos2 x 5) равна 1 хотя бы при одном значении х?
Решение. Рассмотрим сумму данных выражений
2
log a (cos 2 x 1) log a (cos 2 x 5) 1.
Пусть t cos2 x 1, t 1;2 тогда
уравнение примет вид
loga t t 4 1
t 2 4t a , (a 0, a 1) .
Построим в прямоугольной
системе координат график
параболы y(t ) t 2 4 t ,
и прямые у = а, учитывая
ОДЗ: t [1;2].
Сумма данного выражения равна 1, при
пересечения параболы с горизонтальной
прямой . По рисунку «считываем» ответ
Ответ: a [5;12]
у
12
5
t
-4
0
1
2

24.

10) Найдите все значения параметра а, для которых при
каждом х из промежутка (4;8] значение выражения
log x 8
2
2
не равно значению выражения
(2a 1)log 2 x
Решим задачу при условии равенства данных выражений.
у
Введем новую переменную:
log2 x t , t 2;3
1
тогда уравнение примет вид:
t 2 8 2a 1 t
2
0
График левой части – парабола f (t),
график правой части – прямая g(t).
-4
f (2) 2 8 4, g (2) (2a 1) 2 4, a 1
2
f (3) 32 8 1,
g (3) (2a 1) 3 1,
-8
1 2
a ;
2
2 3
a
3
2
Значит условие исходной задачи выполняется при
1 2
a ; ;
2 3
3
t

25.

Метод мажорант
Мажорантой называется такое число М, что
либо
либо
для всех
f ( x) , M
f ( x) M
x D( f )

26.

27. Выводы

1. Графический способ и способ мажорант являются наиболее
наглядным, простым и доступным способами решения задач
с параметрами
2. К сожалению, данные методы применимы не всегда .
3. Решение задач с параметрами развивает творческие
способности.

28. Литература

1. Внеурочная работа по математике в контексте реализации
инновационных технологий. Дидактические материалы для
организации деятельности обучаемых: учеб. пособие∕авт.-сост.: А.Т.
Лялькина, Е.В. Чудаева и др. – Саранск, 2007
2. П.И. Горнштейн, В. Б. Полонский, М.С. Якир. Задачи с
параметрами. – М.: Илекса, Харьков: Гимназия, 2003.
3. Б.М.Ивлев, А.М.Абрамов, Ю.П.Дудницен, С.И.Шварцбурд. Задачи
повышенной трудности по алгебре и началам анализа: Учеб.
Пособие для 10-11 кл.сред.шк. - М.: Просвещение, 1990.
4. Экзаменационные материалы для подготовки к единому
государственному экзамену. Математика. ЕГЭ – 2006.
Составитель: Клово А.Г. – 2005.
5. Черняк А.А., Черняк Ж.А. « Алгебра . ЕГЭ:Шаг за шагом»Волгоград: Учитель, 2012