Реляционная алгебра. Лекция 3

1.

Лекция 3 Реляционная
алгебра

2.

Основные понятия
• Реляционная алгебра - теоретический язык запросов, наглядно
описывающий выполняемые над отношениями действия.
• Цель реляционной алгебры — обеспечить запись реляционных
выражений, позволяющих определять:
• области выборки;
• области обновления;
• правила поддержки целостности данных ;
• производные переменные-отношения, т.е. те данные, которые
должны быть включены в представления базы данных;
• требования устойчивости, т.е. данные, которые должны быть
включены в контролируемую область для некоторых операций
управления параллельным доступом к информации;
• ограничения защиты.

3.

Операторы
• Реляционная алгебра в том виде, в котором она была определена Э.Ф. Коддом, состоит из двух групп по четыре оператора.
• 1. Традиционные операции над множествами (но модифицированные с учетом того, что их операндами являются отношения, а
не произвольные множества): объединение, пересечение,
разность и декартово произведение.
• 2. Специальные реляционные операции: выборка, проекция, соединение, деление.

4.

Унарные и бинарные операции
• Операция реляционной алгебры может выполняться
• над одним отношением (например, проекция), унарной
• над двумя отношениями (например, объединение) такая операция
называется бинарной.
• При выполнении бинарной операции участвующие в операциях
отношения должны быть совместимы по структуре.
• Совместимость структур отношений означает совместимость
имен атрибутов и типов соответствующих доменов. Частным
случаем совместимости является идентичность (совпадение).

5.

Объединение
Объединение возвращает отношение, содержащее все кортежи, которые
принадлежат либо одному из двух заданных отношений, либо им обоим

6.

Пересечение
Пересечение возвращает отношение, содержащее все кортежи, которые
принадлежат одновременно двум заданным отношениям

7.

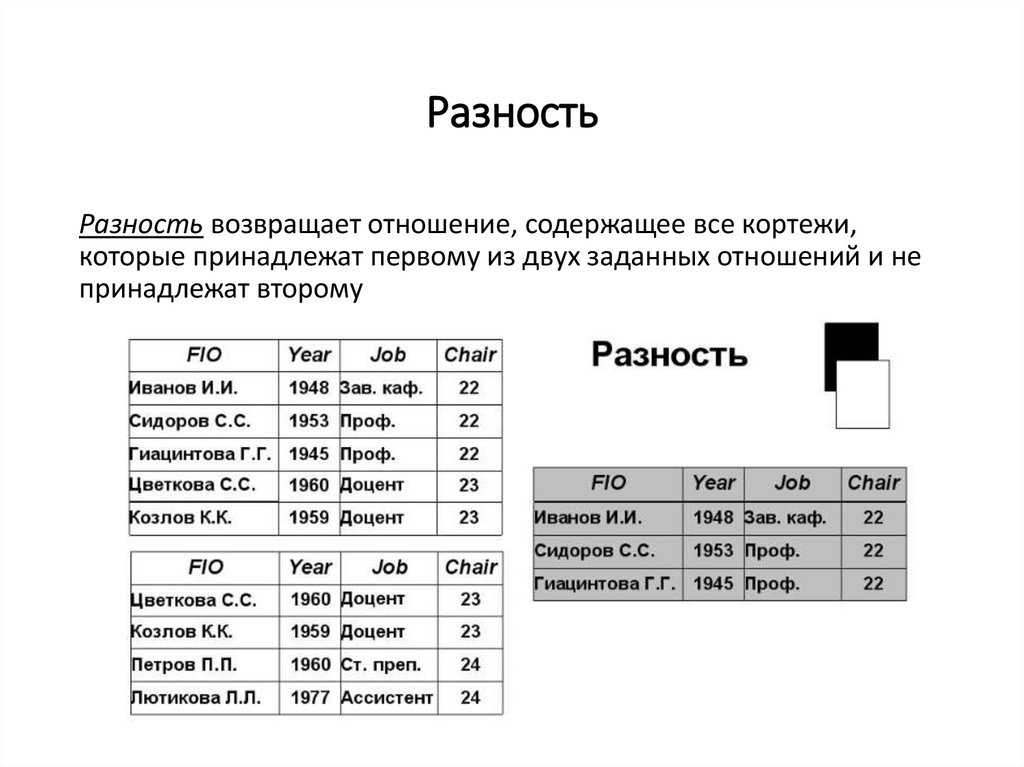
Разность
Разность возвращает отношение, содержащее все кортежи,
которые принадлежат первому из двух заданных отношений и не
принадлежат второму

8.

Произведение
Произведение возвращает отношение, содержащее все возможные кортежи, которые являются сочетанием двух кортежей,
принадлежащих соответственно двум заданным отношениям

9.

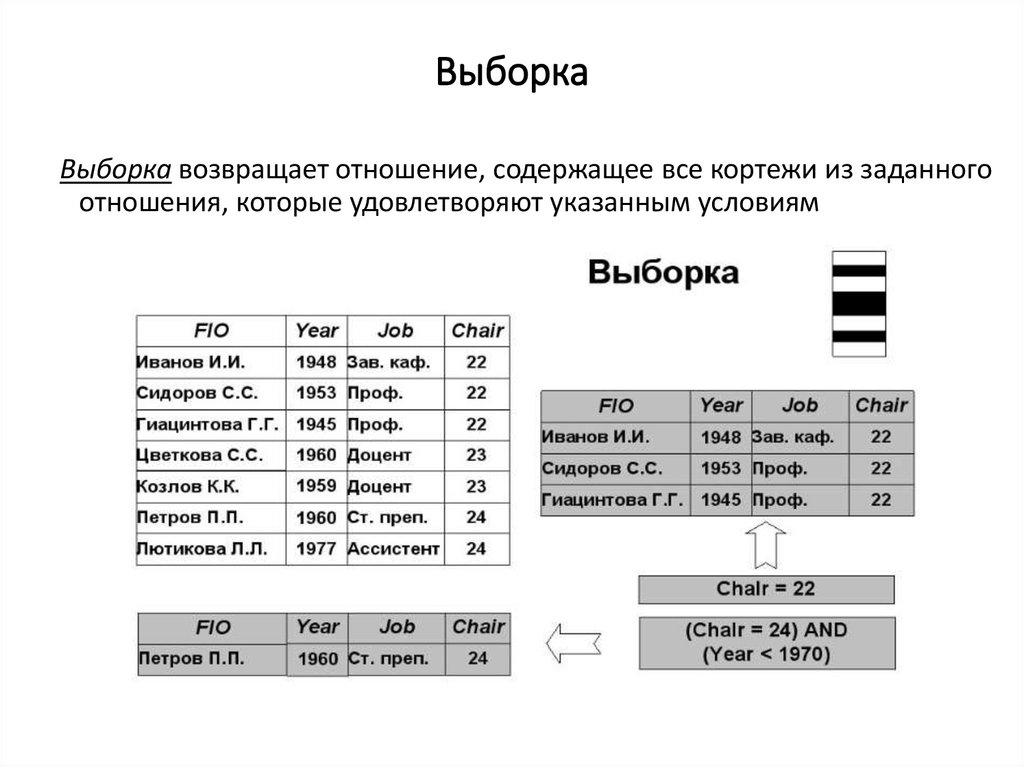
Выборка
Выборка возвращает отношение, содержащее все кортежи из заданного
отношения, которые удовлетворяют указанным условиям

10.

Проекция
Проекция возвращает отношение, содержащее все кортежи (подкортежи) заданного отношения, которые остались в этом отношении после исключения из него некоторых атрибутов

11.

Соединение
• Соединение возвращает отношение, содержащее все возможные
кортежи, которые представляют собой комбинацию атрибутов
двух кортежей, принадлежащих двум заданным, при условии,
что в этих двyx комбинированных кортежах присутствуют
одинаковые значения в одном или нескольких общих для
исходных отношений атрибутах (причем эти общие значения в
результирующем кортеже появляются один раз, а не дважды)

12.

13.

Деление
• Деление для заданных двух унарных отношений и одного бинарного возвращает отношение, содержащее все кортежи из
первого унарного отношения, которые содержатся также в
бинарном отношении и соответствуют всем кортежам во втором
унарном отношении

14.

15.

Реляционная замкнутость
Результат выполнения любой операции над отношением также
является отношением, поэтому результат одной операции может
использоваться в качестве исходных данных для другой. Другими
словами, можно записывать вложенные реляционные выражения,
т.е. выражения, в которых операторы сами представлены
реляционными выражениями, причем произвольной сложности.
Эта особенность называется свойством реляционной
замкнутости.