Похожие презентации:
Автоматизация первичной обработки РЛИ
1.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙУНИВЕРСИТЕТ
Военный учебный центр
ОСНОВЫ ОБРАБОТКИ И ПЕРЕДАЧИ
ИНФОРМАЦИИ В АСУ
Тема № 1. Автоматизация первичной
обработки РЛИ
Занятие № 3 Характеристики сигнала и помехи в
тракте первичной обработки.
Руководитель занятия:
преподаватель кафедры АСУ ВКС
майор запаса Бейльман С.В.
2.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТУчебные вопросы:
1.Основные характеристики случайных
процессов.
2.Статистические модели помехи, сигнала.
3.Статистические модели смеси сигнала с
помехой.
4.Характеристики помехи на входе УПО.
Модели смеси сигнала с помехой на входе
УПО.
2
3.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТЛитература
1. В.Н. Ратушняк, С.В. Бейльман, И.В. Тяпкин. Основы
обработки
и
передачи
информации
в
автоматизированных системах управления. Часть I
Первичная обработка радиолокационной информации.
– Красноярск: СФУ ВУЦ, 2020 – С. 51 - 73.
2. А.Я Матов, П. Я. Сависько, Б.М. Герасимов. Основы
обработки и передачи информации в АСУ РТВ ПВО. –
Киев: КВИРТУ ПВО, 1985. – С.7–16.
3. Справочник офицера воздушно-космической обороны /
под. ред. С.К. Бурмистрова. – Тверь: ВА ВКО, 2008. –
С.523–527.
3
4.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВопрос №1
Основные характеристики
случайных процессов.
4
5.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТХАРАКТЕРИСТИКИ СИГНАЛА И ПОМЕХИ В ТРАКТЕ
ПЕРВИЧНОЙ ОБРАБОТКИ
Наиболее существенными задачами теории обработки РЛИ
являются обоснование оптимальных правил получения сведений о
целях (синтез оптимальных устройств обработки), нахождение
приемлемых упрощений оптимальных структур с целью их
технической реализации и оценка показателей качества обработки РЛИ.
Решение перечисленных задач при первичной обработке РЛИ связано с
заданием характеристик сигнала и помехи, т. е. с обоснованием их
моделей.
В данном разделе рассматриваются физические явления, анализ
которых позволяет выяснить характеристики сигнала и помехи на
выходе антенны РЛС. Последующий анализ преобразований исходных
процессов в типовых элементах приемного тракта приводит к
описанию модель видеосигнала U(t), поступающего от РЛС в АСУ.
Поскольку процессы на выходе антенны РЛС являются случайными, то
решение указанной задачи лежит в рамках теории вероятностей,
некоторые положения которой включены в содержание раздела.
5
6.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТОсновные характеристики случайных процессов
При обсуждении данного вопроса не ставится задача
описания всей совокупности характеристик случайного
процесса, тем более со строгими выкладками их введения.
Скорее, это напоминание основных понятий и положений
некоторых разделов теории вероятностей, которые наиболее
часто используются в теории обработки РЛИ.
Случайный
(или
стохастический)
процесс
представляет собой изменения во времени физической
величины, которые заранее предсказать невозможно.
Примерами случайных процессов могут служить как
помеха, так и сигнал. Действительно, до приема
электромагнитной волны ряд параметров сигнала неизвестен. В
противном случае задачи первичной обработки не имели бы
смысла. Еще более непредсказуема помеховая составляющая
радиолокационного сигнала.
6
7.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТКоличественно случайный процесс описывается случайной
функцией времени ξ(t), которая может принимать различные
значения с заданной вероятностью. Если наблюдать случайный
процесс, например, на выходе антенны РЛС, то на каждом
временном интервале длительностью Т будем регистрировать
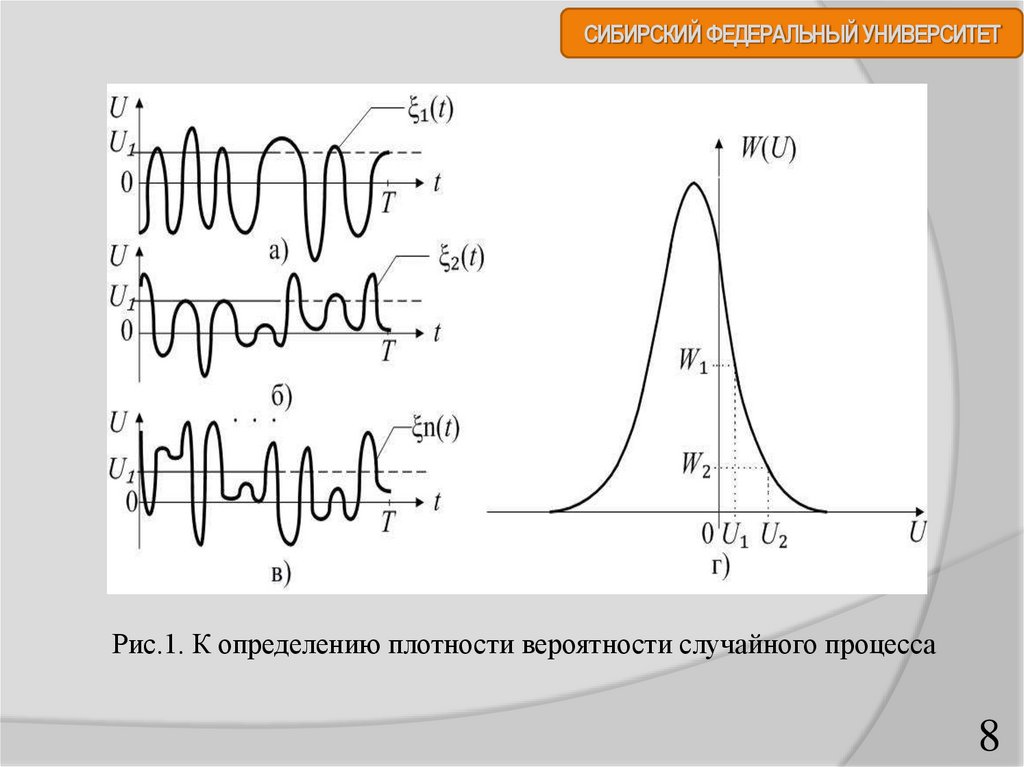
различные функции времени (рис.1, а, б, в).
Любая из этих функций, ставшая полностью известной после
приема сигнала, называется реализацией случайного процесса.
Для описания свойств случайного процесса используют
статистические (вероятностные) характеристики совокупности
реализаций - плотность вероятности и спектральную плотность
мощности.
Перечисленные
характеристики
не
являются
исчерпывающими, однако вполне достаточны для описания
статистических моделей сигнала и помехи, а также для анализа
процесса обработки радиолокационной информации.
7
8.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРис.1. К определению плотности вероятности случайного процесса
8
9.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТПлотность вероятности (или дифференциальная функция
распределения) представляет собой неслучайную функцию,
которая характеризует, насколько вероятны те или иные значения
случайного процесса.
Для выявления физического смысла плотности вероятности
рассмотрим один из вариантов ее определения по совокупности
реализаций случайного процесса.
Пусть имеется достаточно большое число (см. рис.1, а, б, в)
реализаций случайного процесса ξ(t). Зададим некоторый уровень
U1 из диапазона изменения функции ξ(t). Тогда можно подсчитать
число пересечений W1 уровня U1 с реализациями ξ1(t), ... ξn(t).
Аналогично для фиксированного значения U2 получим
некоторое число W2. Если такую же оценку провести для всех
значений U в диапазоне от ∞ до + ∞, то можно построить кривую
W(U), которая (рис.1, г) представляет собой плотность
вероятности случайного процесса ξ(t). Очевидно, что более
вероятным значениям случайного процесса соответствуют
большие значения плотности вероятности.
9
10.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРазмерность плотности вероятности W(U) обратна размерности
своего аргумента. Действительно, получаемые значения WK
характеризуют число пересечений, относящихся к бесконечно
малому интервалу ΔU в окрестности уровня Uк. В частности, если
U напряжение [В], то размерность плотности вероятности -[1/В].
Напомним основные свойства плотности вероятности.
Вероятность попадания значений случайного процесса ξ(t) в
некоторый интервал [U1, U2] определяется соотношением:
U2
P U1 ξ t U 2 W U dU
(1)
U1
Величина этой вероятности равна площади под кривой
распределения W(U) на интервале [U1, U2 ]. На рис.2 данная
площадь P1 выделена штриховкой.
10
11.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТW(U)
P₁
U₁
0 U₂
P₂
U₃
U
Рис. 2 Пояснение свойств плотности вероятности
Аналогично находится вероятность превышения некоторой
фиксированной величины, например, U3, значениями случайного
процесса ξ(t):
P ξ t U 3 W U dU
(2)
U3
11
12.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВероятности (2) соответствует площадь заштрихованной
области Р2 на рис.2.
В частном случае, если рассматривать бесконечный интервал
от -∞ до +∞, то вероятность попадания значений случайного процесса
в указанный интервал равна единице, так как данное событие
является достоверным. Поэтому:
P ξ t W U dU 1
(3)
Согласно выражению (3), введенное понятие плотности
вероятности W(U) с использованием оценочных значений (W1, W2, и
т. д.) требует уточнения. После нахождения зависимости W(U)
рассмотренным способом необходимо рассчитать площадь под
кривой W(U). Если эта площадь отлична от единицы, т. е. условие (3)
не выполняется, то функцию W(U) следует умножить на
нормирующий коэффициент С = const, обеспечивающий выполнение
указанного условия.
12
13.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВведение понятия спектральной плотности мощности
связано с определенными особенностями, которые следует отметить.
Пусть имеется достаточно большое число реализаций
случайного процесса ξ(t). Каждой реализации соответствует
некоторый спектр:
Fi ( f )exp{ jφi ( f )}
(4)
где Fi ( f ) – амплитудно-частотный спектр i-й реализации;
φi ( f ) - фазочастотный спектр i-й реализации;
i = 1, 2,..., n – число реализаций случайного процесса.
Статистическое
усреднение
спектров
случайного процесса приводит к нулевому спектру.
реализаций
13
14.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТЧтобы избежать нулевого результата, усреднение выполняют
не по спектральной амплитуде, а по спектральной мощности, т. е. не
по гармоникам спектров
Fi ( f )exp{ jφi ( f )}
а по гармоникам квадрата спектров
Gi ( f k ) Fi ( f ) exp{ jφi ( f )}
В
результате
спектральной мощности
2
усреднения
совокупности
значений
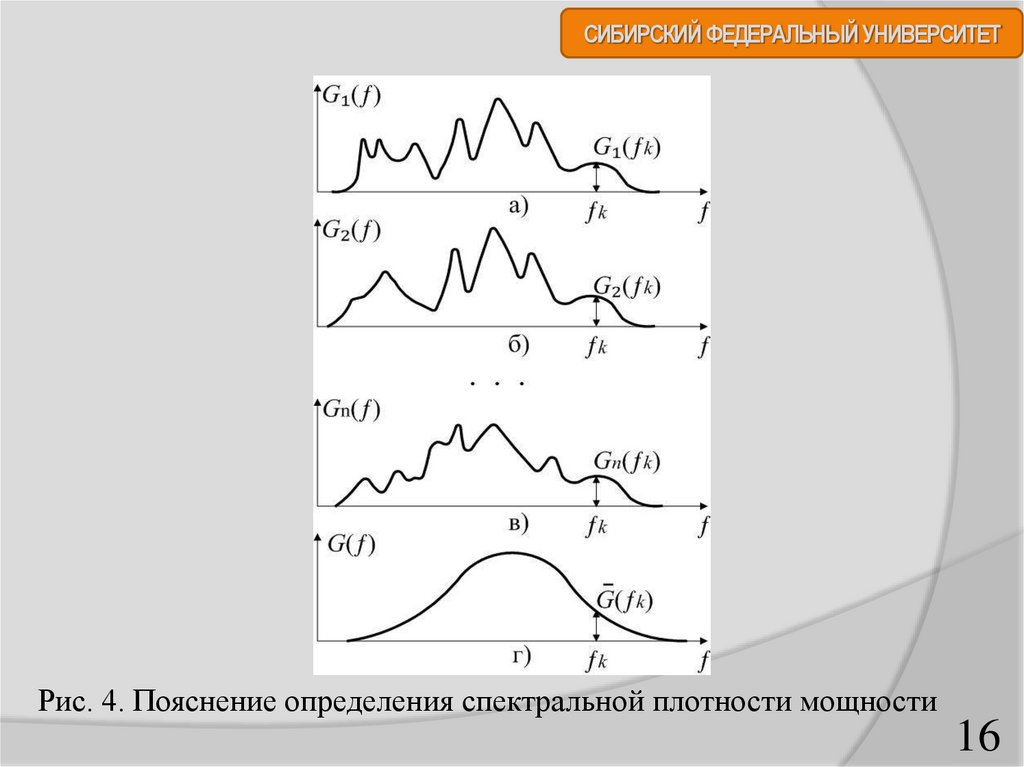
G ( f ) на частоте f k (рис.4, а, б, в),
i
k
находим неслучайную величину, отличную от нуля:
1 n
G ( f k ) Gi ( f k )
n i 1
(5)
14
15.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТСтатистическое усреднение гармоник Gi ( f )
на каждой из частот приводит к неслучайной функции
G( f )
которая представляет собой спектральную плотность мощности
случайного процесса (рис.4, г).
Спектральная
плотность
мощности
характеризует
усредненное распределение мощности случайного процесса по
частотам. Ее размерность определяется отношением мощности к
спектральной полосе частот, т. е. энергией:
мощность
[G ( f )]
мощность время = энергия [Дж.].
полоса частот
Поэтому спектральную плотность мощности
G( f )
также называют энергетическим спектром.
15
16.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРис. 4. Пояснение определения спектральной плотности мощности
16
17.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТЕсли энергетический спектр процесса сосредоточен в
относительно узкой полосе частот около некоторой фиксированной
частоты f , то случайный процесс называется узкополосным.
0
Условие узкополосности определяется неравенством f
где f - ширина энергетического спектра.
В противном случае т.е. при f
называется широкополосным.
f0
f 0 , случайный процесс
17
18.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВопрос №2
Статистические модели помехи,
сигнала.
18
19.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТНе всякий физический процесс следует считать сигналом.
Сигналом является только тот физический процесс, который
содержит информацию, то есть некоторую совокупность сведений о
состоянии или положении некоторого объекта. В качестве сигнала,
таким образом, можно рассматривать любой физический процесс при
условии, что некоторые его параметры изменяются в соответствии с
переносимым сообщением.
Сигналы можно разделить на естественные и специально
создаваемые. К естественным сигналам относят, например, световые
сигналы от физических объектов окружающего мира, космические
сигналы, электрические поля биологических объектов и др.
Примерами специально создаваемых могут служить сигналы,
посылаемые радиолокационной станцией, сигналы лазеров для
зондирования атмосферы и др.
19
20.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТДетерминированный сигнал, или сигнал с полностью
известными параметрами (регулярный) имеет вид
y( t ) u( t ) n( t ), u( t ) U m ( t )cos 0t ( t )
где
U m ( t ) - амплитуда сигнала;
0
- несущая частота сигнала;
( t ) - функция угловой модуляции;
- начальная фаза колебаний.
Все это точно известные неслучайные величины. Считается,
что мы знаем время запаздывания сигнала, эффективную площадь
рассеяния цели, форму сигнала и все параметры его модуляции. Эта
модель наиболее идеализирована.
20
21.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТКвазидетерминированные сигналы, или сигналы со
случайными параметрами имеют вид
y( t ) U m ( t , ) n( t )
где - вектор случайных параметров сигнала.
Возможны два случая:
а) сигнал со случайной начальной фазой φ:
u( t, ) um ( t )cos 0t ( t )
где φ – неизвестная начальная фаза, распределенная равномерно
от 0 до 2π, т.е. w0 ( ) 1 / ( 2 );
б) сигнал со случайной фазой φ и флуктуирующей
амплитудой aum ( t ) ,
где φ - неизвестная начальная фаза с распределением w0 ( ) 1 / ( 2 )
а - коэффициент флуктуации амплитуды с распределением
, таким образом
2
a
a
w( a )
exp 2 u( t, ,a ) aU m ( t )cos 0t ( t )
a
2 a
21
22.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТСтатическая модель помехи
Характеристики помехи на выходе антенны
Флюктуационная помеха (флюктуационный шум) постоянно
присутствует на выходе антенны РЛС. Природа флюктуационного
шума обусловлена большим числом случайных факторов. Основными
из них являются излучение небесного фона, в том числе Солнца
(космический шум), вторичное излучение атмосферы (атмосферный
шум), тепловое излучение Земли, шумы антенны за счет конечной
проводимости ее металлических элементов, собственные шумы
усилителей приемника РЛС (мощность этих шумов обычно
пересчитывается к выходу антенны).
Перечисленные факторы, в свою очередь, являются результатом
весьма большого числа независимых случайных явлений. Поэтому,
согласно центральной предельной теореме теории вероятностей, при
большом числе случайных независимых процессов их сумма
флюктуационной
помехи
представляет собой
нормальный
(гауссовый) случайный процесс.
22
23.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТПлотность вероятности нормального случайного процесса
описывается выражением:
1
(U U ) 2
W (U )
exp{
},
2
2σ
2πσ
(6)
где σ – среднеквадратическое значение нормального случайного
процесса (его квадрат, т.е. σ2 представляет дисперсию);
U – среднее значение процесса;
U – независимая переменная.
Очевидно, что положительные и отрицательные значения
помехи равновероятны, т.е. ее среднее равно нулю. Поэтому
распределение мгновенных значении флюктуационной помехи
описываются зависимостью:
1
U2
Wфл (U )
exp{ 2 },
2σ фл
2πσ фл
(7)
23
24.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТСпектральная плотность мощности Gфл ( f ) флуктуационного
шума зависит от физической природы его образования, а также участка
канала связи, где он рассматривается.
Обычно спектральная плотность мощности Gфл ( f )
флуктуационного шума постоянна в широком диапазоне частот, т. е.
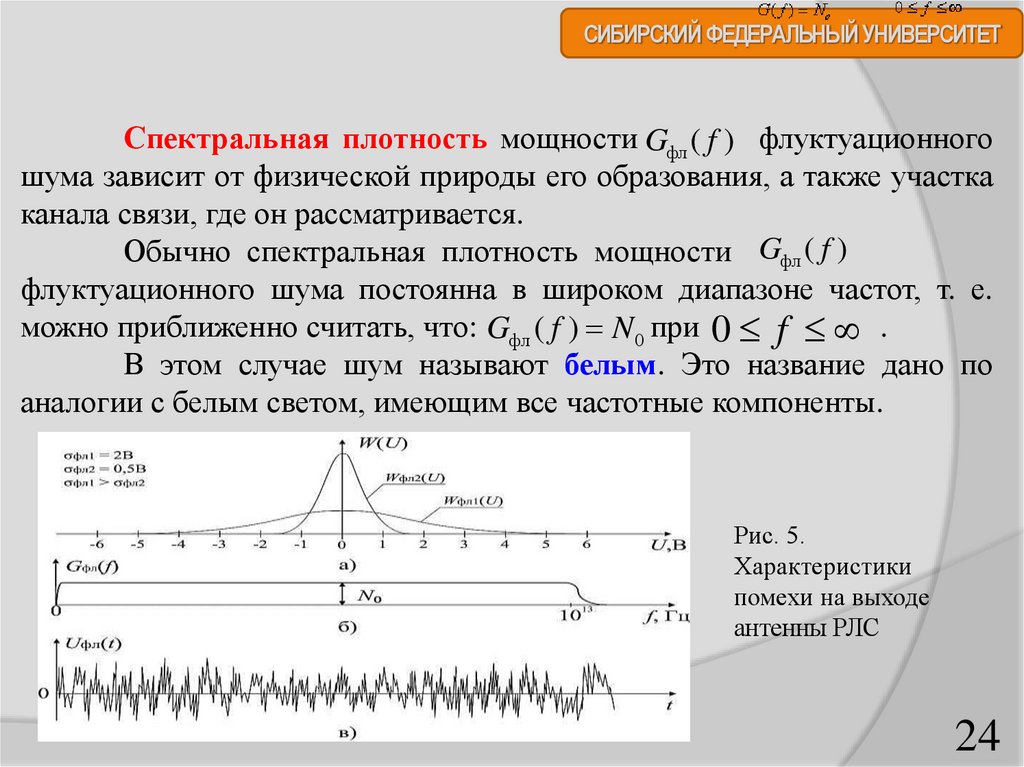
можно приближенно считать, что: Gфл ( f ) N 0 при 0 f .
В этом случае шум называют белым. Это название дано по
аналогии с белым светом, имеющим все частотные компоненты.
Рис. 5.
Характеристики
помехи на выходе
антенны РЛС
24
25.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТХарактеристики помехи на выходе приемника
Поскольку у флюктуационной помехи отсутствует какаялибо упорядоченность, то наблюдается нарушение навязывания
свободных колебаний в избирательных элементах приемника.
Поэтому с течением времени амплитуда Uфл(t) и фаза
φфл(t) навязанных колебаний изменяются по случайному закону.
Интервал
корреляции
τк
(интервал
сохранения
статистических связей) функций Uфл(t) и φфл(t) зависит от
полосы пропускания П приемника ( τк = 1/П), т. е. чем уже полоса
пропускания приемника, тем выше добротность избирательных
элементов и, следовательно, тем более продолжительное время
свободные колебания сохраняют статистическую связь как
амплитуды, так и фазы.
25
26.
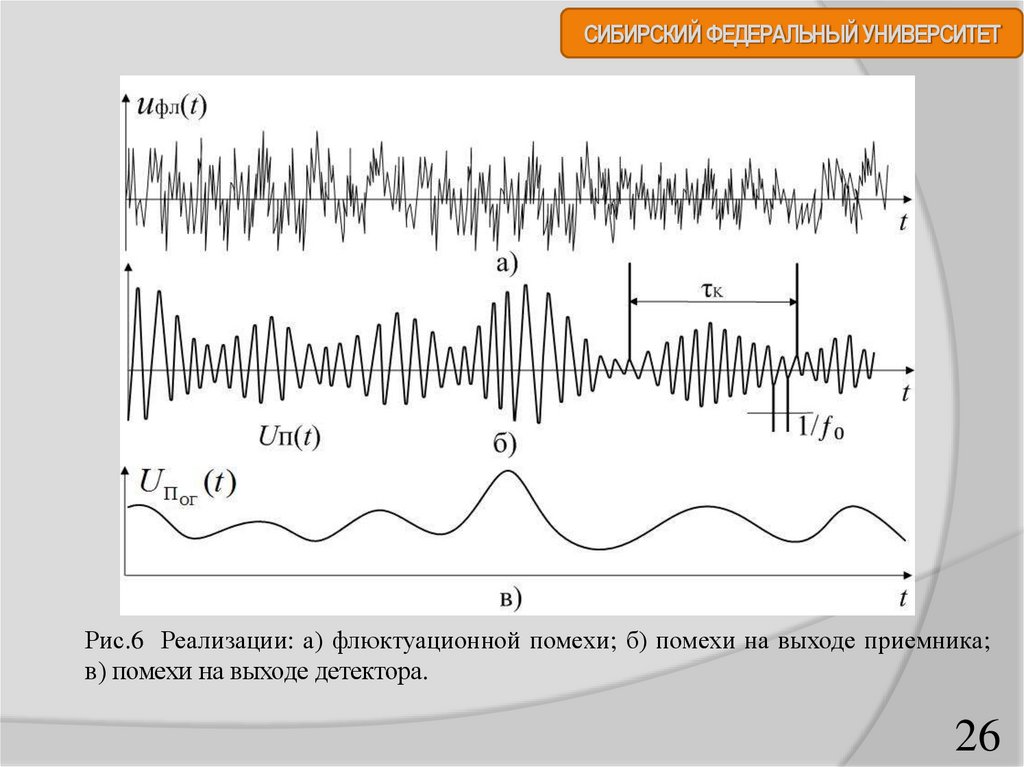
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРис.6 Реализации: а) флюктуационной помехи; б) помехи на выходе приемника;
в) помехи на выходе детектора.
26
27.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТФлюктуационная помеха (рис. 6, а), воздействуя на
избирательные элементы приемника, вызывает существенные
гармонические колебания
в окрестности резонансной
U фл (t )
частоты f 0 (рис. 6, б)
U фл (t ) U фл (t )cos[2πf 0 φфл (t )]
(8)
27
28.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВопрос №3
Статистические модели смеси
сигнала с помехой.
28
29.
Сибирский федеральный университетх
t
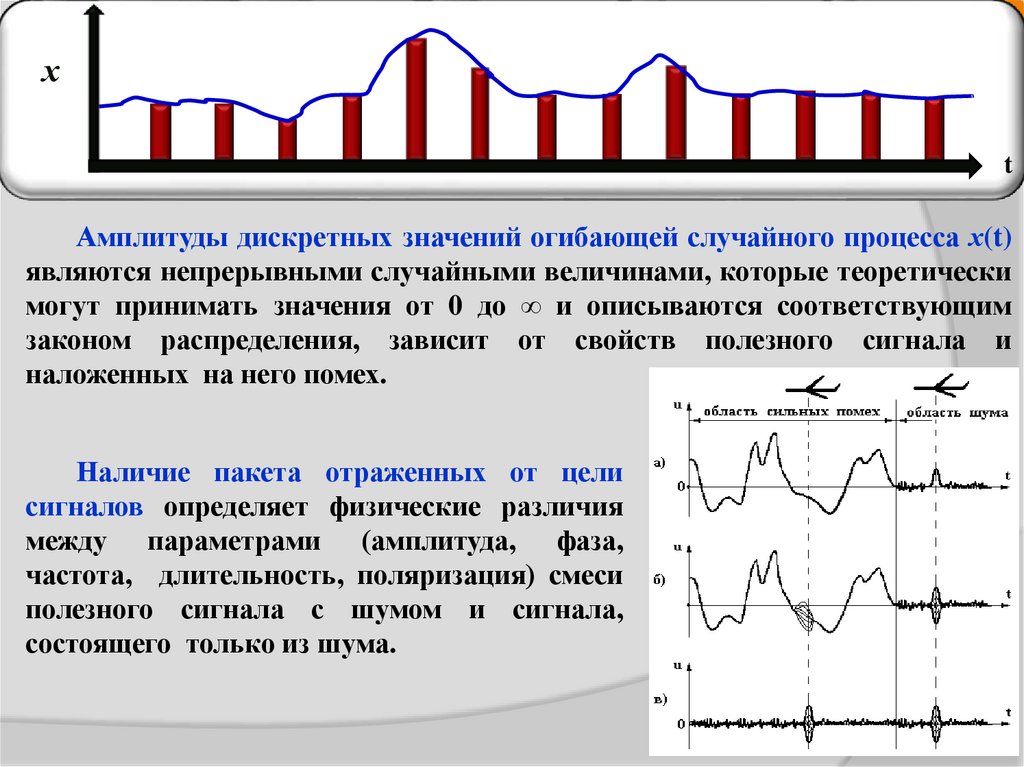
Амплитуды дискретных значений огибающей случайного процесса х(t)
являются непрерывными случайными величинами, которые теоретически
могут принимать значения от 0 до ∞ и описываются соответствующим
законом распределения, зависит от свойств полезного сигнала и
наложенных на него помех.
Наличие пакета отраженных от цели
сигналов определяет физические различия
между параметрами (амплитуда, фаза,
частота, длительность, поляризация) смеси
полезного сигнала с шумом и сигнала,
состоящего только из шума.
30.
Сибирский федеральныйуниверситет
Так, выборка смеси сигнала нефлюктуирующей
цели и узкополосной
шумовой помехи описывается обобщенным законом Рэлея-Райса:
x2 a2
W ( x / a) x exp
I 0 ( xa)
2
(9)
х = (S сигнала + N шума) / шума – нормированная по среднеквадратическому значению
шума величина выборки (амплитуды дискретного значения) огибающей смеси
сигнал /шум;
S сигнала – величина полезного сигнала в составе выборки;
N шума – величина шума в составе выборки;
шума – среднеквадратическое значение шума в составе выборки;
а = S сигнала / шума – нормированная по среднеквадратическому значению
шума величина полезного сигнала (отношение сигнал/шум);
IО (ха) - модифицированная функция Бесселя 1-го рода нулевого порядка;
W(х/а) - условная плотность распределения вероятности амплитуды
выборки при наличии в её составе полезного (отраженного ) сигнала
31.
университетСибирский
x 2 a 2федеральный
W ( x / a) x exp
I 0 ( xa)
(10)
2
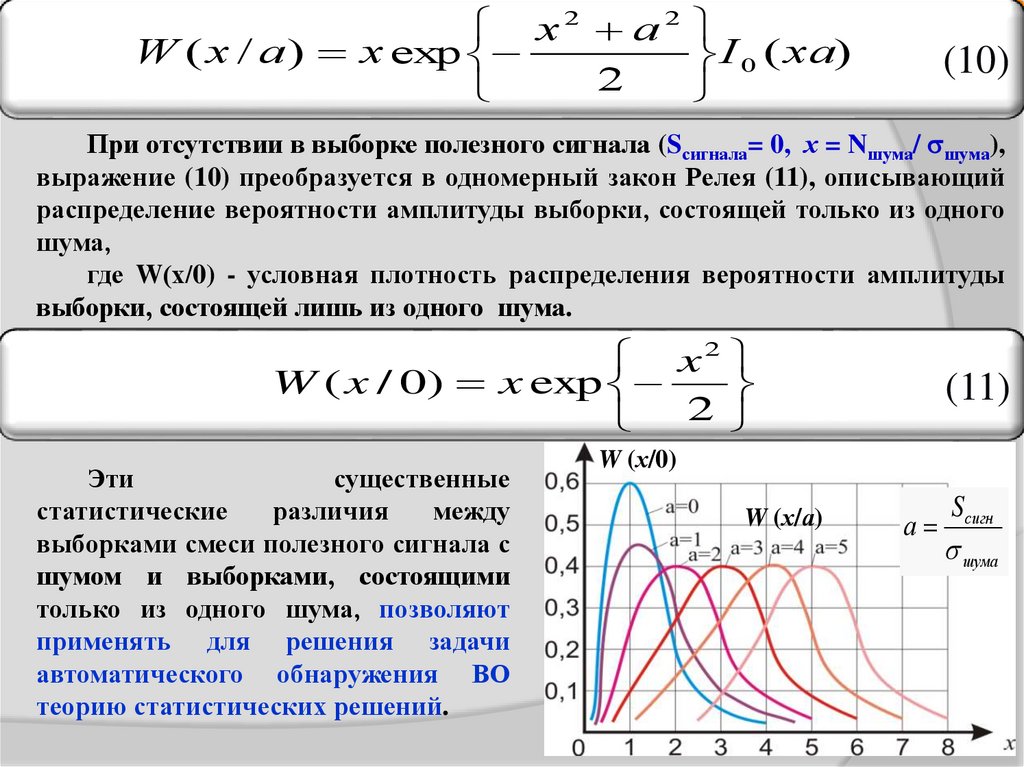
При отсутствии в выборке полезного сигнала (Sсигнала= 0, х = Nшума/ шума),
выражение (10) преобразуется в одномерный закон Релея (11), описывающий
распределение вероятности амплитуды выборки, состоящей только из одного
шума,
где W(х/0) - условная плотность распределения вероятности амплитуды
выборки, состоящей лишь из одного шума.
x2
W ( x / 0) x exp
2
Эти
существенные
статистические
различия
между
выборками смеси полезного сигнала с
шумом и выборками, состоящими
только из одного шума, позволяют
применять для решения задачи
автоматического обнаружения ВО
теорию статистических решений.
(11)
W (х/0)
W (х/а)
S сигн
а
шума
32.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВопрос №4
Характеристики помехи на входе
УПО. Модели смеси сигнала с
помехой на входе УПО.
32
33.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТХарактеристики помехи на входе УПО
Пусть реализация помехи (8), представляющая нормальный
случайный процесс, поступает на вход амплитудного детектора.
На
выходе
последнего
выделяется
напряжение,
пропорциональное огибающей Uфлог(t) высокочастотного колебания
Uфл(t). Статистические характеристики данного видеосигнала
представляют искомую модель помехи на входе устройства
первичной обработки. Даже качественный анализ реализаций
Uфлог(t) и Uфл(t) по эпюрам напряжений на рис. 6 позволяет сделать
вывод о существенных изменениях характеристик помехи в
результате ее детектирования.
Во-первых, процесс Uфлог(t), представляющий собой
результат амплитудного детектирования, принимает значения только
одной полярности. В дальнейшем для определенности будем
полагать, что Uфлог(t)> 0. Следовательно, плотность вероятности
продетектированного процесса отлична от нуля только в области
положительных значений аргумента U.
33
34.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВо-вторых, если для гауссовой помехи Uфл(t) маловероятны
значительные выбросы [Uфл(t) > 3σфл], то для продетектированного
процесса Uфлог(t) маловероятны не только выбросы, но и малые
значения амплитуды. Действительно (см. рис. 6, б и 6, в), высокочастотное колебание Uфл(t) наиболее часто принимает нулевое
значение. Однако его огибающая Uфлог(t), как правило, не достигает
нулевого уровня.
Поэтому следует ожидать, что распределение помехи на
выходе детектора стремится к нулю в области как больших, так и
малых значений U.
Типичный график плотности вероятности амплитуды помехи
на выходе детектора (на входе УПО), не противоречащий выводам
качественного анализа, приведен на рис. 7. Данное распределение
называется релеевским и аналитически описывается выражением:
U
U2
Wфл (U ) 2 exp{ 2 }. (12)
σфл
2σфл
где
Wфл (U ) - плотность вероятности
амплитуды помехи на входе УПО
σ фл – дисперсия нормального случайного
процесса.
34
2
35.
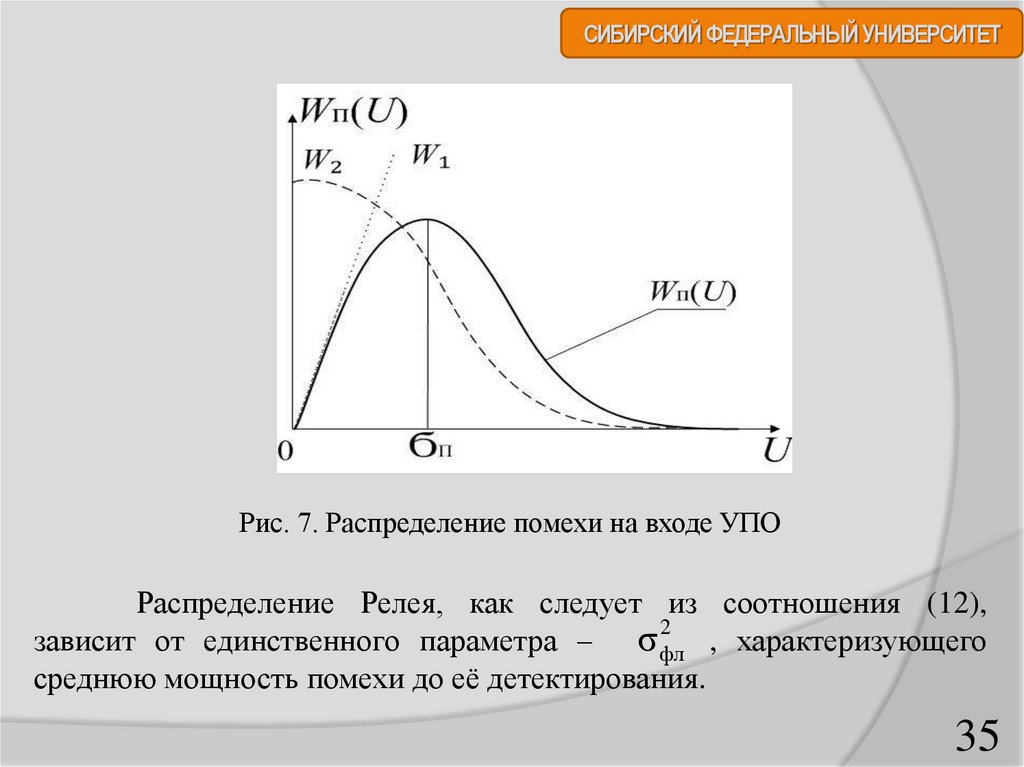
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРис. 7. Распределение помехи на входе УПО
Распределение Релея, как следует из соотношения (12),
2
зависит от единственного параметра – σ фл , характеризующего
среднюю мощность помехи до её детектирования.
35
36.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТМодели смеси сигнала с помехой на входе УПО
Смесь помехи и сигнала с полностью известными параметрами.
Пусть сигнал относится к первой статистической модели, для
которой Uc(t)=Uc=const, φс(t)=φc=const. Для оценки характера
амплитуды смеси сигнала с помехой Uсп(t) приведем ряд фрагментов
векторного суммирования их комплексных амплитуд, относящихся к
различным интервалам корреляции τk.
Используя рис.8, проведем анализ зависимости амплитуды
Uсп(t) от соотношения амплитуд сигнала Uс и помехи Uп(t) при
фиксированной разности фаз φс и φп (t).
При малых амплитудах сигнала суммарный вектор (рис.8, а)
практически не отличается от помехового. Можно поэтому ожидать,
что распределение амплитуды Uсп(t) при условии Uс ˂ Uп (t)
приближается к распределению Релея.
Реализации Uсп(t) на входе УПО в таком случае фактически
представляют помеху.
36
37.
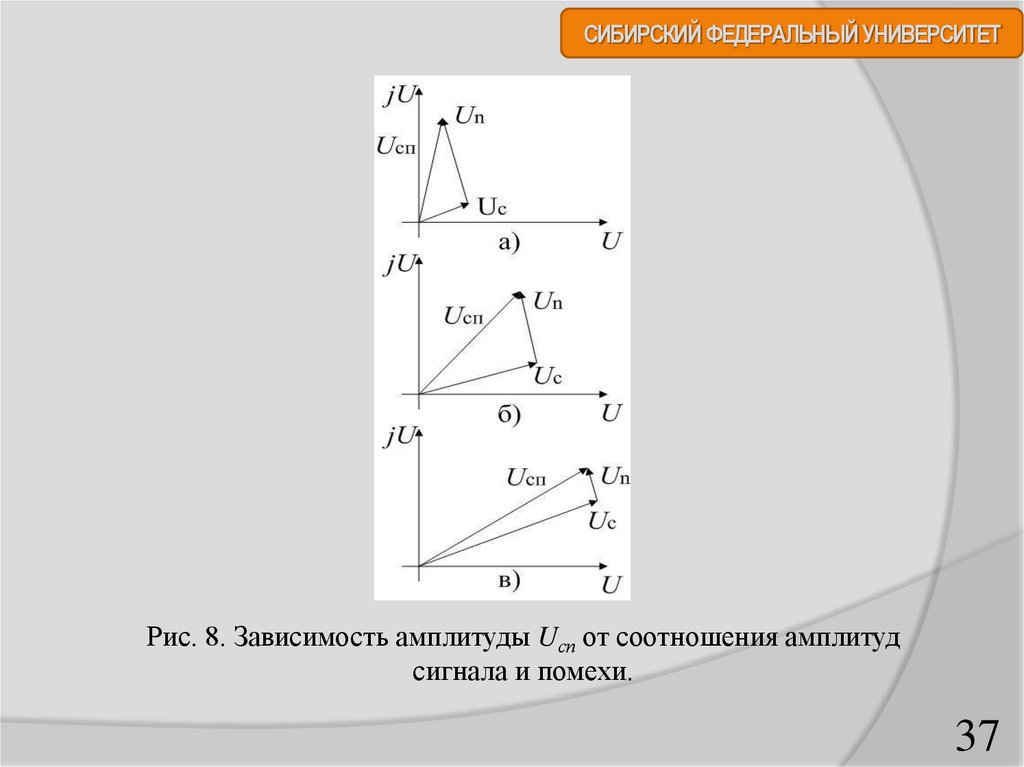
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРис. 8. Зависимость амплитуды Uсп от соотношения амплитуд
сигнала и помехи.
37
38.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТЕсли амплитуда сигнала и помехи одного порядка (рис. 8, б),
то по сравнению с предыдущей ситуацией напряжение на входе УПО
существенно зависит от обеих составляющих аддитивной смеси.
В среднем значения Uсп(t) несколько превышают средний
уровень помеховой составляющей Uп(t) . Однако не исключена
вероятность малых значений амплитуды Uсп(t). Это не трудно
проверить, полагая, что Uс ≈ Uп (t) , а φс = φп – π .
Если амплитуда сигнала значительно превышает средний
уровень помехи (рис. 8, в), то амплитуда Uсп(t) в основном
определяется полезной составляющей аддитивной смеси. Поэтому при
Uсп(t) ˃ Uп маловероятны ситуации подавления сигнала помехой.
Приведенные примеры свидетельствуют о том, что
распределение амплитуды Uсп(t) смеси полностью известного сигнала
с помехой зависит от статистических характеристик помехи и
амплитуды сигнала. Данное распределение, как можно показать,
подчиняется обобщенному закону Релея (называемому также
законом Райса) (13).
38
39.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТU
U 2 U с2
UU с
Wсп (U ) 2 exp{
}J 0 ( 2 )
2
σп
2σп
σп
(13)
В данном выражении J(·) – модифицированная функция
Весселя первого рода нулевого порядка:
2π
UU с
1
UU с
J0 ( 2 )
exp{ 2 cos(φ-φс )}dφ.
σп
2π 0
σп
(14)
Графики распределения Райса при различных значениях
амплитуды полезного сигнала






























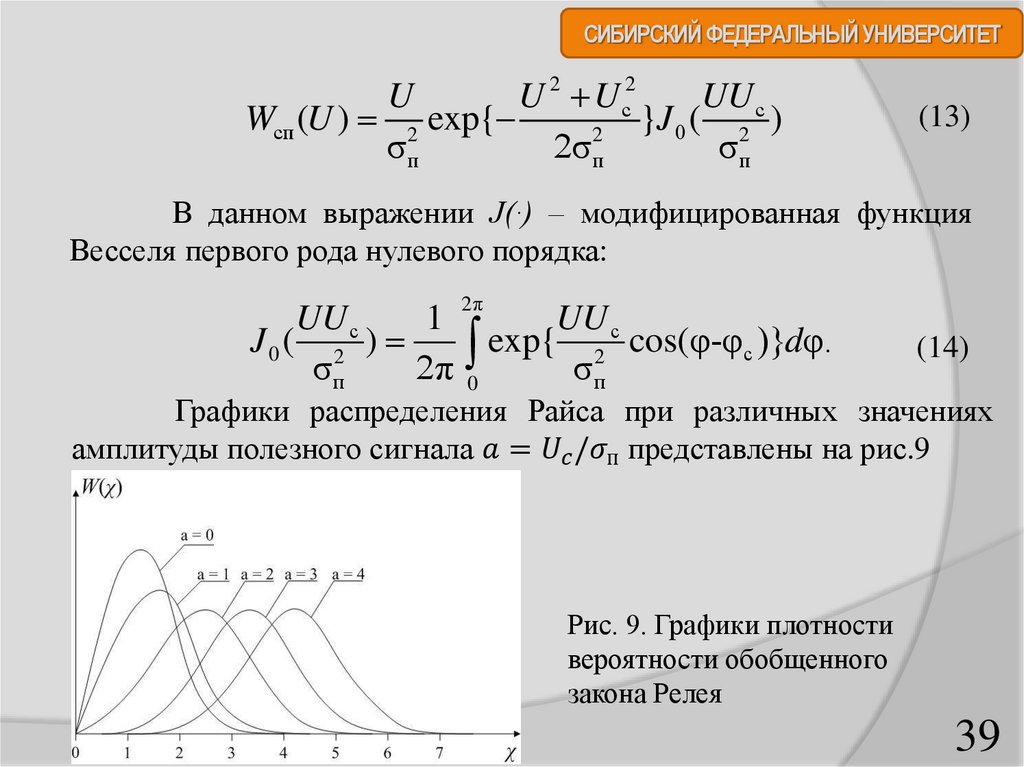


 Военное дело
Военное дело








