Похожие презентации:
Радиолокационные системы
1.
Военно-инженерный институтУчебный военный центр
Отдел «Радиолокационного вооружения РТВ ВВС»
Дисциплина
«РАДИОЛОКАЦИОННЫЕ СИСТЕМЫ»
Часть 1. Теоретические основы радиолокации
2.
1Дать характеристику отраженным сигналам,
шумам и помехам, раскрыв содержание основных
физических факторов, определяющих параметры и
модели их формального представления.
3.
21. Модели и характеристики отраженных сигналов.
2. Статистические характеристики шумов и
помех.
3. Структура и математическая модель мешающих
отражений.
4.
35.
46.
5Информацию о РЛЦ получают из принятого отраженного от
цели радиолокационного сигнала. При теоретическом решении
задач радиолокации требуется математический аналог реального
сигнала. В этой связи в радиолокации рассматривают ряд моделей
отраженного сигнала, позволяющих в той или иной степени
учитывать его параметры.
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОТРАЖЕННОГО СИГНАЛА
В зависимости от характера изменения параметров сигнала
во времени различают:
а) сигналы с полностью известными параметрами
x (t ) X (t ) cos 0t (t ) ;
б) сигналы со случайной начальной фазой:
x(t , ) X (t ) cos 0t (t ) ,
где β - случайная начальная фаза модулирующего множителя;
7.
6в) сигналы со случайной амплитудой и начальной фазой
x(t , , b) b X (t )cos 0t (t ) ,
где b, β - амплитуда и фаза случайного модулирующего множителя.
В общем случае параметр является функцией времени,
т.е. b = b(t), и рассматривают комплексный модулирующий множитель ;
B (t ) b(t )e
j
г) сигналы вида пачки из М флуктуирующих по амплитуде
радиоимпульсов со случайными начальными фазами
M
x(t , 1 , 2 ,... N , b1 , b2 ,...bN ) bk X k (t )cos 0t k (t ) k .
k 1
По характеру временной структуры отраженных сигналов
различают когерентные и некогерентные сигналы.
К когерентным сигналам относят колебания с жестко заданной
структурой (жестко связанными временными элементами).
Сигналы с независимыми амплитудно-фазовыми множителями (пачка
флуктуирующих по амплитуде радиоимпульсов со случайными начальными
фазами) считают уже некогерентными.
8.
7Для математического описания случайных параметров
вводят плотности вероятностей. Фаза β обычно распределена
по равномерному закону в пределах 0,2π, т.е.
1
, 0 2
Р( ) 2
.
0
0, 2
Амплитудные флюктуации носят более сложный характер и
для различных целей могут описываться различными законами
распределения. Одним из них, охватывающим широкий класс РЛЦ,
является закон Релея
2b exp b 2 , b 0
Р(b)
.
0 ,
b 0
Этот закон хорошо описывает флюктуации амплитуды сигнала,
отраженного от целей, имеющих большое число «блестящих точек»
примерно одинаковой интенсивности.
9.
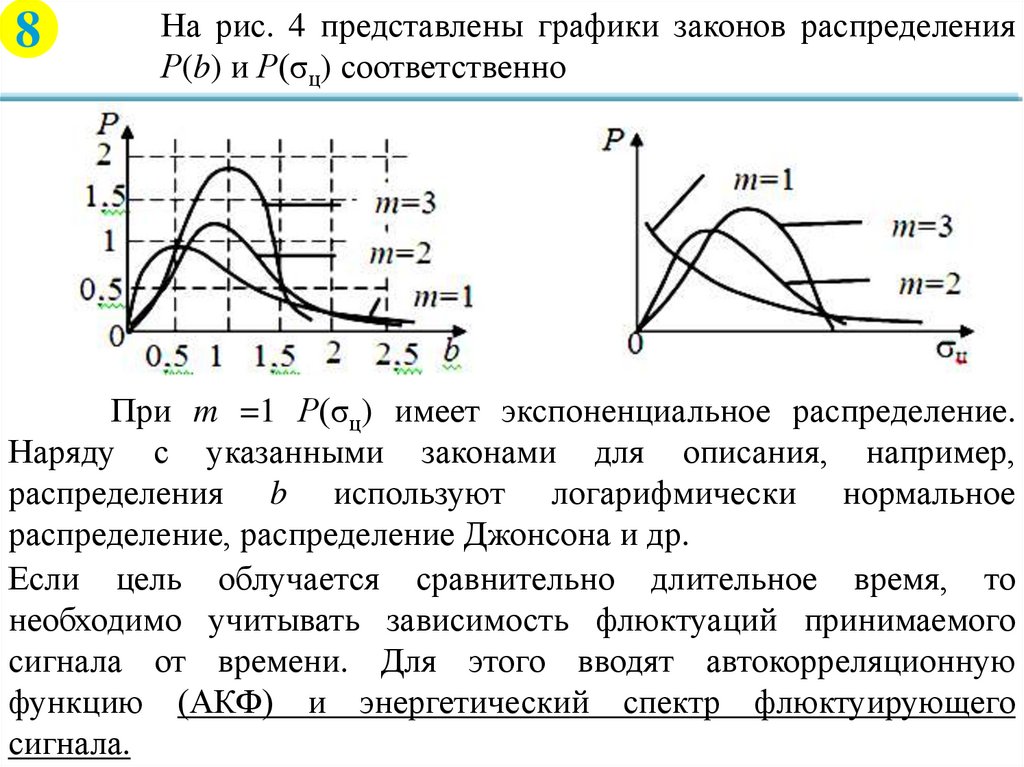
8На рис. 4 представлены графики законов распределения
Р(b) и Р(σц) соответственно
При m =1 Р(σц) имеет экспоненциальное распределение.
Наряду с указанными законами для описания, например,
распределения b используют логарифмически нормальное
распределение, распределение Джонсона и др.
Если цель облучается сравнительно длительное время, то
необходимо учитывать зависимость флюктуаций принимаемого
сигнала от времени. Для этого вводят автокорреляционную
функцию (АКФ) и энергетический спектр флюктуирующего
сигнала.
10.
9АВТОКОРРЕЛЯЦИОННАЯ ФУНКЦИЯ И ЭНЕРГЕТИЧЕСКИЙ
СПЕКТР ФЛЮКТУАЦИЙ ОТРАЖЕННОГО СИГНАЛА
Эти характеристики показывают степень случайности
флуктуаций отраженного сигнала, т.е. модулирующего
множителя (t). АКФ задается соотношением
T
1
RB M B t B t lim B t B t dt ,
T T
0
где
комплексно
сопряженные
значения
B(t ), B -(t )
модулирующего множителя;
T - интервал усреднения. Вещественная АКФ равна Re RB .
RB
B
.
Вводят также нормированную АКФ
RB 0
Энергетический спектр модулирующего множителя находится по
Rв(τ):
S B ( f ) RB e j 2 f d .
11.
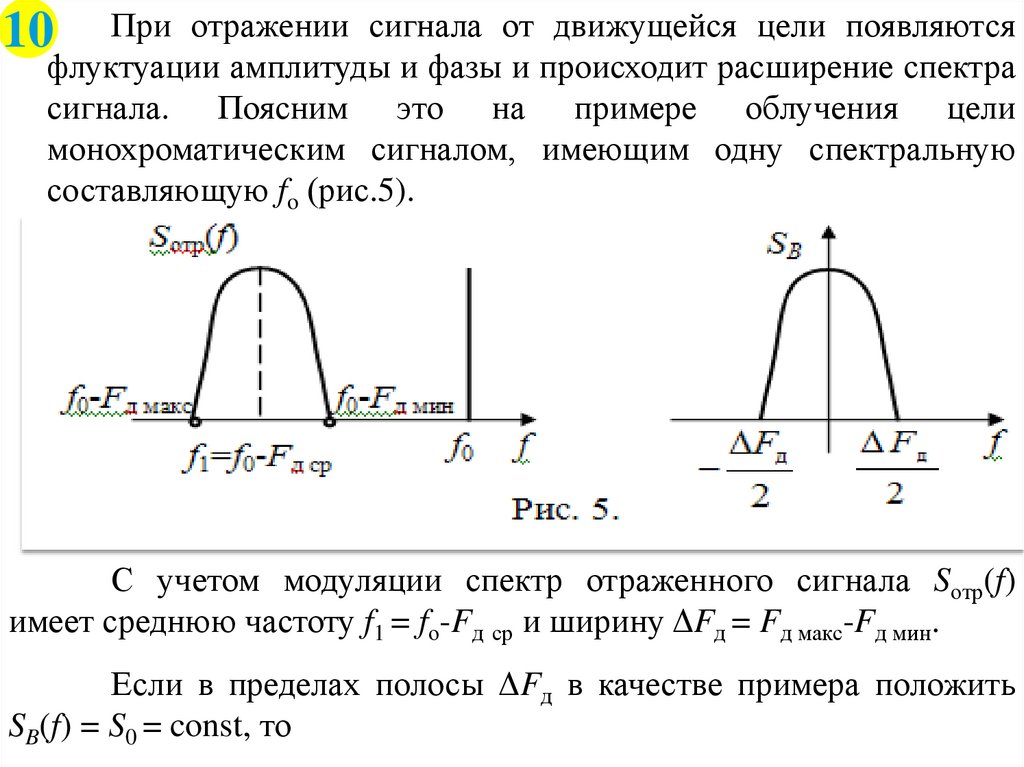
При отражении сигнала от движущейся цели появляютсяфлуктуации амплитуды и фазы и происходит расширение спектра
сигнала. Поясним это на примере облучения цели
монохроматическим сигналом, имеющим одну спектральную
составляющую fo (рис.5).
10
С учетом модуляции спектр отраженного сигнала Sотр(f)
имеет среднюю частоту f1 = fо-Fд ср и ширину ΔFд = Fд макс-Fд мин.
Если в пределах полосы ΔFд в качестве примера положить
SB(f) = S0 = const, то
12.
11Fд
2
RB RB ( ) S B ( f ) e j 2 f df So e j 2 f df
RB (0) S0 Fд , а
Fд
2
sin Fд
B B
.
Fд
Кривая ρВ(τ) для рассматриваемого случая представлена на рис.6.
13.
12Интервал времени, характеризующий ширину пика автокорреляционной функции, наприме
1
τк
Fд
параметр
может быть назван временем
корреляции. Время корреляции связано с шириной
энергетического спектра модулирующего множителя
обратно пропорциональной зависимостью. В случае
сильной статистической связи последовательных значений
сигнала имеет место узкий спектр флюктуаций и
наоборот.
Функции автокорреляции широко используются при
анализе влияния флюктуаций на обнаружение и измерение
параметров радиолокационных сигналов.
14.
131. Таким образом, реальный отраженный сигнал имеет
случайные амплитуду и фазу. Флюктуационные
составляющие параметров отраженного сигнала
называют шумом цели.
2. Для полного описания отраженного сигнала
необходимо знать плотность распределения его
амплитуд и фаз. Важное значение для анализа
погрешности сигналов и выбора схем их обработки
имеют автокорреляционная функция и энергетический
спектр отраженного сигнала.
15.
1416.
Флуктуационная помеха является наиболее распространеннойв радиолокации. К ней относятся внутренний шум приемного
устройства РЛС и наиболее распространенный вид преднамеренных
помех - шумовые помехи.
n2
Одномерная плотность распределения y(t) = n(t)
2
1
определяется выражением
p ( n)
e 2σ
15
п
2π
где σ2 - дисперсия (мощность) помехи.
Важной энергетической характеристикой шумов является
спектральная плотность мощности.
Спектральная плотность мощности внутренних шумов
определяется соотношением
0
N0=kT (Кш+tа-1)
где k =1,38∙10-23 Дж/град – постоянная Больцмана;
Т0 - абсолютная температура в град. Кельвина (обычноТ0=300 К);
Кш - коэффициент шума приемника;
tа= Та/Т0 - относительная шумовая температура антенны;
Та – абсолютная шумовая температура антенны.
При tа=1 или Кш >(tа-1) получим N0=kT0 Кш .
17.
Для решения задач синтеза и анализа в радиолокациииспользуют две основные модели флуктуационной помехи:
квазибелый и белый шум.
16
Квазибелый шум.
Квазибелым шумом называют шум, имеющий постоянную
спектральную плотность мощности в полосе частот (рис.8):
N(f)
N(f)
N0
N f N 0 , при 0 f f max
fmax
f
N0
fmin
N f N 0 при
fmax
f
Рис. 8.
f min f f max
18.
Скорость изменения мгновенныхопределяется корреляционной функцией
17
значений
помехи
T
1
R lim n(t )n(t )dt R 0 ,
T T
0
где ρ(τ) - нормированная корреляционная функция.
Или, учитывая связь N(f) и R(τ), запишем
R N ( f )cos 2 f df .
0
Подставляя поочередно в последнее выражение значения N(f)
из (2) и (3) получим соответственно
sin 2 f max
R( ) N 0 cos 2 f N 0 f max
2 f max
0
f max
и
sin П
R( ) N 0 cos 2 f dt N 0 П
cos 2 f 0
П
f min
(4)
f max
,
(5)
19.
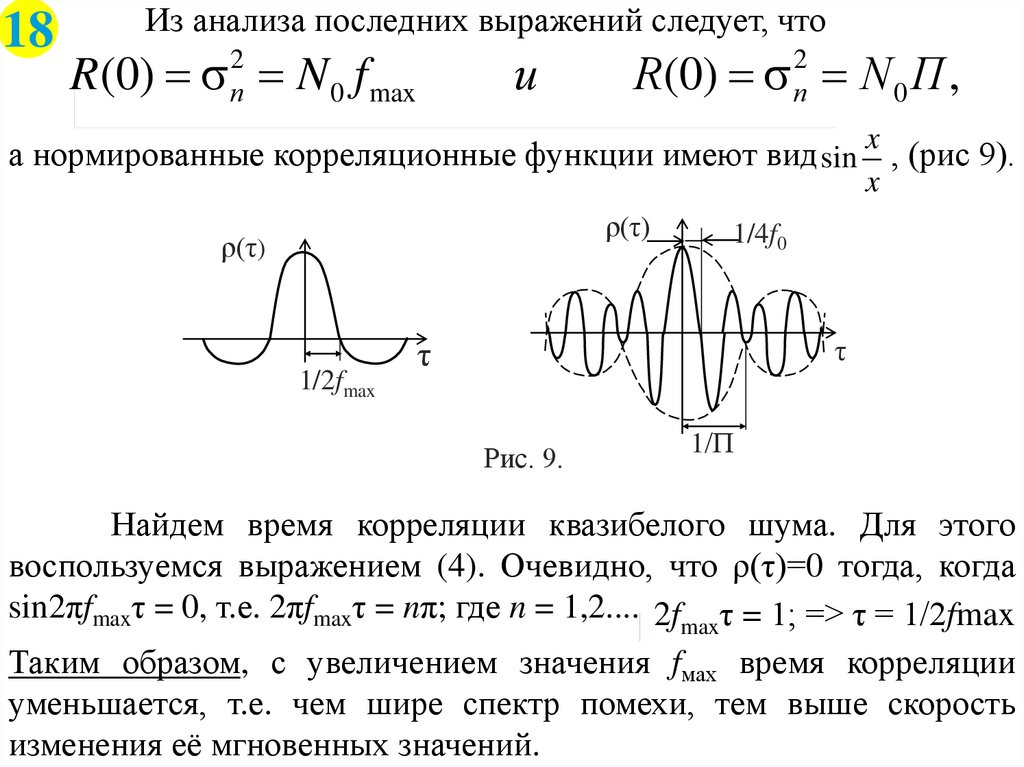
18Из анализа последних выражений следует, что
R(0) 2п N 0 f max
и
R(0) 2п N 0 П ,
x
x
а нормированные корреляционные функции имеют вид sin , (рис 9).
ρ(τ)
ρ(τ)
1/2fmax
1/4f0
τ
τ
Рис. 9.
1/П
Найдем время корреляции квазибелого шума. Для этого
воспользуемся выражением (4). Очевидно, что ρ(τ)=0 тогда, когда
sin2πfmaxτ = 0, т.е. 2πfmaxτ = nπ; где n = 1,2.... 2fmaxτ = 1; => τ = 1/2fmax .
Таким образом, с увеличением значения fмах время корреляции
уменьшается, т.е. чем шире спектр помехи, тем выше скорость
изменения её мгновенных значений.
20.
Белый шум.19
Белым шумом называется модель флуктуационной помехи с
постоянной спектральной мощностью N0 на бесконечном интервале
частот (т.е. fмакс → ∞). Для белого шума справедливы две модели
спектральной плотности, представленные на рис.10.
N(f)
N(f)
N0
N0/2
f
f
Рис. 10.
Заменив
cos2πfτ
по
формуле
корреляционную функцию белого шума
Эйлера,
найдем
N0
N 0 j 2 f
N0
j 2 f
j 2 f
R( )
e
e
df
e
df
( ) (6)
2 0
2 0
2
где e
2 f
df ( ) - дельта - функция Дирака (рис. 11), обладающая
свойством
21.
20δ τ
при τ 0 δ(τ)
.
0, при τ 0
0
Рис. 11.
τ
22.
Из выражения (6) следует, что белый шум является дельтакоррелированным. Это означает бесконечно высокую скоростьизменения его мгновенных значений и бесконечную мощность.
Поэтому белый шум является абстракцией, удобной при анализе
устройств обработки.
При синтезе оптимальных алгоритмов обработки РЛ
сигналов, кроме корреляционных и спектральных характеристик
помехи, требуется знание плотности вероятности её распределения.
Многомерная плотность вероятности помехи
Случайную реализацию y(t) = n(t) можно однозначно задавать
некоторой совокупностью своих дискретных значений. В этом
случае принятая реализация
n(t) = n(t 1,t 2,...,t m).
Такая замена возможна на основании теоремы
Котельникова, согласно которой любая функция с
1
ограниченным спектром полностью определяется
t f max .
2
отсчетом своих значений, взятыми через интервал
21
23.
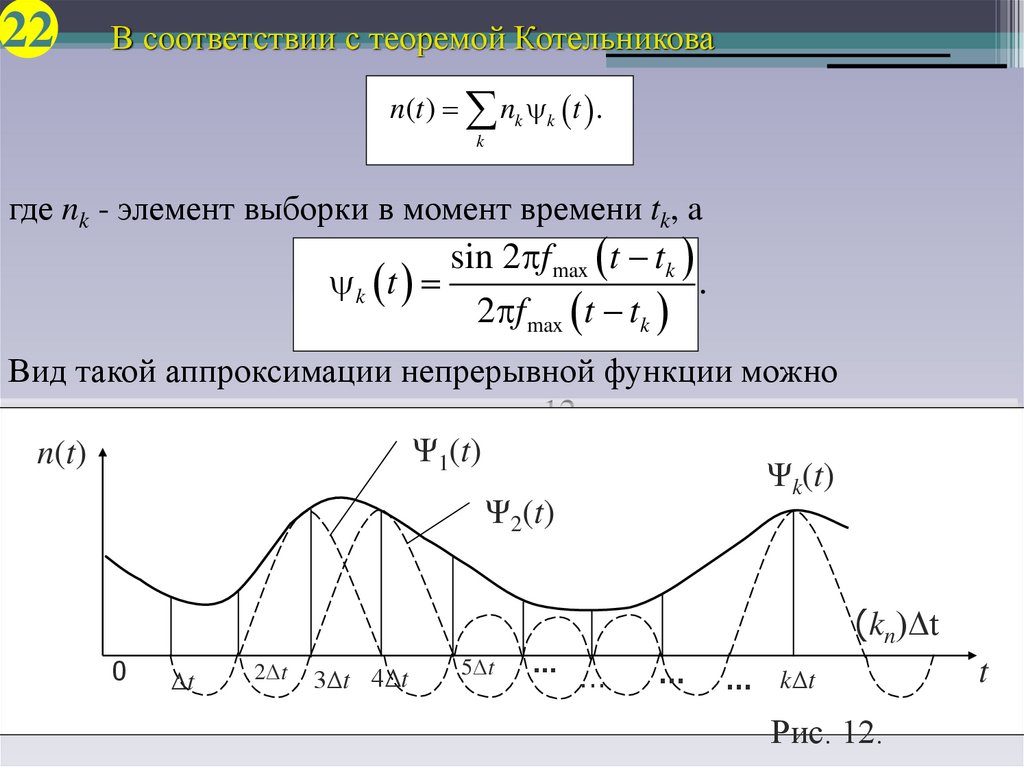
22В соответствии с теоремой Котельникова
n(t ) nk k t .
k
где nk - элемент выборки в момент времени tk, a
sin 2 f max t tk
k t
.
2 f max t tk
Вид такой аппроксимации непрерывной функции можно
проиллюстрировать с помощью рис.12.
Ψ1(t)
n(t)
Ψk(t)
Ψ2(t)
(kn)Δt
0
Δt
2Δt
3Δt 4Δt
5Δt
...
...
…
…
kΔt
Рис. 12.
t
24.
23 Замечательным свойством такого представления является то,что коэффициенты разложения ψk(t) - некоррелированы, а значит
отсчёты
yk
независимые
случайные
величины.
Некоррелированность объясняется тем, что интервал дискретизации
Δt = tk+1-tk равен интервалу корреляции помехи.
Поэтому при таком представлении помехи ее статистика может
быть представлена плотностью вероятностей
P n P n1 , n2 , ...
С учетом теоремы Котельникова элементы вектора n независимы,
поэтому
P n П P nk
k
где Р(nk) - одномерная плотность.
Подставляя в Р(nk) значение мощности помехи, например, для
квазибелого шума, получим
1
P nk
e
2
nk 2
2
2
1
e
2 N 0 f max
nk 2
2 N 0 f max
t
e
N 0
nk2 t
N0
.
25.
24В общем случае, используя векторно-матричную
запись, плотность вероятности m-элементной выборки
нормально распределенного квазибелого шума можно
представить в виде:
m
2
2
P n 2
1 T
exp 2 n n .
2
26.
25Таким
образом,
полной
статистической
характеристикой колебаний помехи является плотность
вероятности. Колебания помехи описывают также с
помощью корреляционной функции и спектральной
плотности мощности.
27.
2628.
Мешающие отражения обусловлены вторичным излучениемповерхностно и объёмно распределенных отражателей, которые
занимают достаточно большой объем пространства, превышающий
разрешаемый объем. Мешающие отражения представляют собой
результат наложения случайно возникающих элементарных
сигналов с флюктуирующими амплитудой и фазой и поэтому
является случайным процессом с нормальной плотностью
распределения вероятностей.
27
Общей особенностью мешающих отражателей является
прямая связь с зондирующим сигналом. Поэтому математическая
модель мешающих отражений почти не отличается от
математической модели полезных отраженных сигналов
N
N (t ) bk (t ) X (t tk )e
j 2 ( f 0 Fдк ) t k ( t ) bk
,
k 1
где N - количество
отражателей.
элементарных
участков
пространства
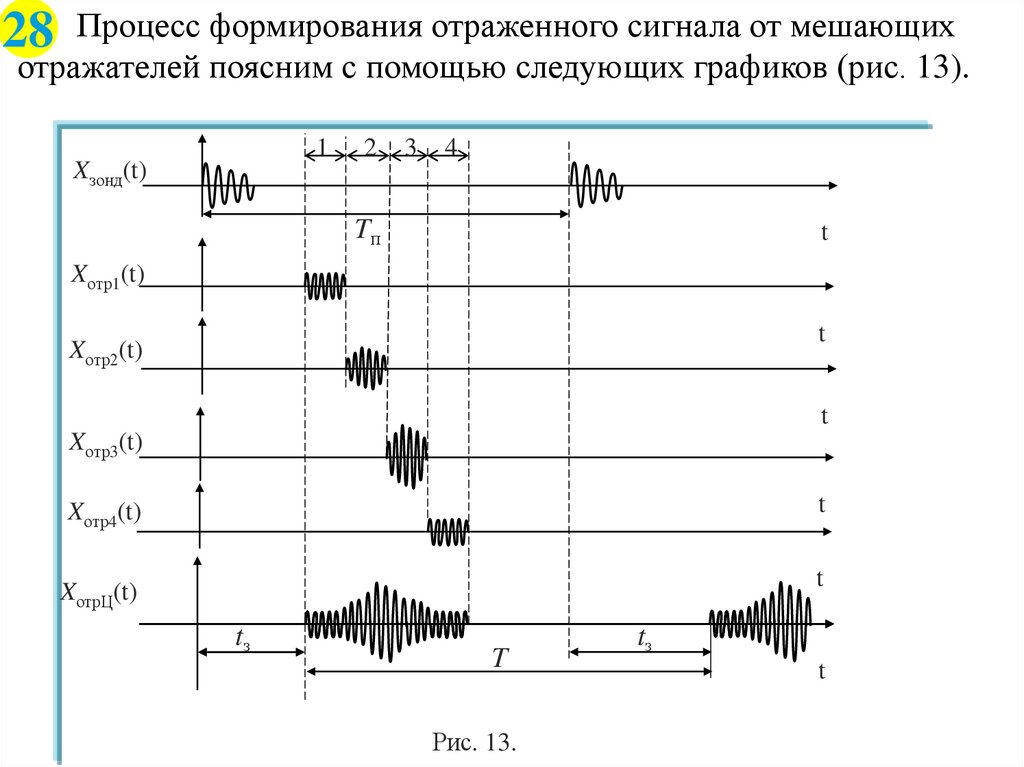
29.
28 Процесс формирования отраженного сигнала от мешающихотражателей поясним с помощью следующих графиков (рис. 13).
1
Xзонд(t)
2
3
4
Tп
t
Xотр1(t)
t
Xотр2(t)
t
Xотр3(t)
t
Xотр4(t)
t
XотрЦ(t)
tз
T
Рис. 13.
tз
t
30.
29Когда отражатели сосредоточены в отдельных разрешаемых
объёмах, помеха носит имитирующий характер, когда они
распределены и захватывают несколько разрешаемых объемов, маскирующий.
Внутрипериодная структура мешающих отражений подобна
структуре шумового процесса, длительность которого соответствует
реальной протяженности элементарных отражателей, попавших в
характеристику направленности антенны РЛС.
При отражении ЗС от различных частей протяженного
облака рассеивателей происходит «размывание» его закона
модуляции. Это приводит к тому, что модель мешающих отражений
нельзя представить в отличие от полезного сигнала произведением
комплексной огибающей и комплексного закона модуляции ЗС (tз1 ≠
tз2 ≠ tз3 ≠...≠ tзk и т.д.).
Энергетический спектр мешающих отражений определяется
как прямое преобразование Фурье от корреляционной функции
Sп ( f ) Rп ( )e j 2 t dt.
31.
30 Поэтомупри
использовании
периодического
ЗС
энергетический спектр мешающих отражений оказывается
гребенчатым с огибающей, определяемой энергетическим
спектром одиночного зондирующего сигнала (рис. 14).
Отраженные от целей сигналы и маскирующие пассивные
помехи имеют определенные отличия, связанные с различиями
целей и отражателей, создающих пассивную помеху. К числу
основных различий можно отнести:
- распределенный характер мешающих отражателей и близкий к
сосредоточенному - блестящих элементов цели. Поэтому, повышая
разрешающую способность по координатам и сокращая при этом размеры
разрешаемого объема (во всяком случае, до размеров, превышающих размеры
самолета), можно добиться улучшения наблюдаемости сигнала на фоне
пассивных помех;
32.
- отличия в поляризации отраженных сигналов наблюдаются, если31пассивная
помеха создается, например, гидрометеорами (дождь, тучи),
состоящими из мелких капель, имеющих форму шара. Если гидрометеоры
облучаются колебаниями с круговой поляризацией, то они отражают
колебания также с круговой поляризацией, но с обратным (если смотреть в
направлении распространения волны) вращением плоскости поляризации.
Если приемная антенна не воспринимает колебания с такой поляризацией, она
тем не менее может принимать колебания от целей, обладающих
несимметрией структуры;
- различия в скорости перемещения мешающих отражателей и цели. Скорость
перемещения наземных мешающих отражателей относительно наземной
радиолокационной станции равна нулю, в то время как представляющие
практический интерес цели перемещаются с достаточно большой скоростью.
Если пассивная помеха создается противорадиолокационными
отражателями, то эти отражатели, будучи сброшены с самолета,
быстро теряют первоначальную скорость, приобретая скорость,
близкую к скорости ветра.
Различия в радиальных скоростях целей и отражателей могут
быть использованы для селекции по скорости (иначе по эффекту
движения цели) называют селекцией движущихся целей (СДЦ).
33.
32Таким образом, из рассмотрения статистических характеристик
мешающих отражений следует:
1. Корреляционные свойства мешающих отражений
определяются
корреляционными
свойствами
ЗС
и
корреляционными свойствами, вносимыми случайными
перемещениями элементарных отражателей.
2. Энергетический спектр мешающих отражений подобен
энергетическому спектру отраженного сигнала, отличается от
него доплеровским сдвигом по частоте Fдп и расширением
спектра.
3. Отличия характеристик и мешающих
позволяют осуществлять их селекцию.
отражений
34.
331. При отражении от движущейся блестящей точки зондирующий
сигнал претерпевает:
- трансформацию временного масштаба;
- трансформацию частоты.
2. При отражении от реальной цели отраженный сигнал приобретает
случайный характер.
3. Основными статистическими характеристиками отраженных
сигналов являются:
- закон распределения вероятностей амплитуды и фазы;
- автокорреляционная функция флуктуаций и
энергетический спектр.
4. Основными статистическими характеристиками шумов и помех
являются:
- плотность распределения мгновенных значений;
- корреляционная функция;
- энергетический спектр.
35.
34 5. Основными моделями внутреннего шума и флуктуационнойпомехи
являются:
- квазибелый шум;
- белый (дельтакоррелированный) шум.
6. Основными отличиями сигналов от целей и мешающих
отражений
являются:
- поляризационные;
- пространственные (распределенный характер помехи и
сосредоточенный - цели);
- скоростные (различия в скорости перемещения мешающих
отражателей и цели).
36.
35Отработать материал лекции в соответствии с
рекомендованной литературой:
Л 1/о с. 49-65

















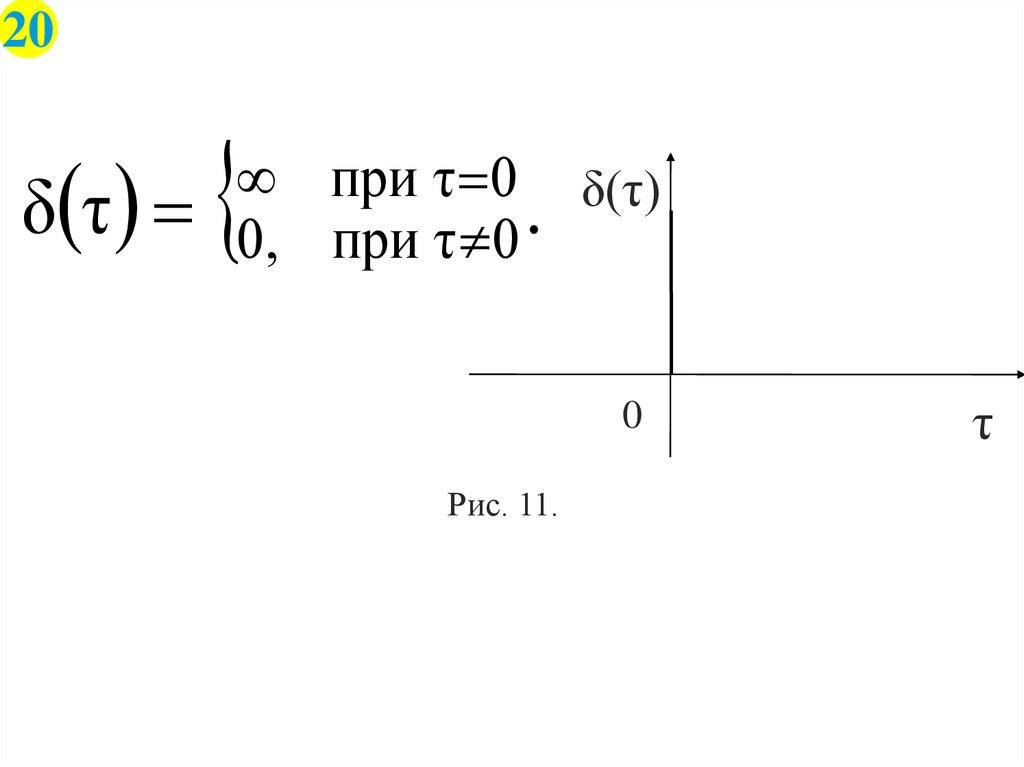













 Военное дело
Военное дело








