Похожие презентации:
Графики функций у = ах2 + n и у = а(х – m)2
1. Графики функций у = ах2 + n и у = а(х – m)2
Графики функций у = ах2 + n2
и у = а(х – m)
2. Цели урока
• расширить сведения о свойствахквадратичной функции;
• ознакомить учащихся с графиками
частных видов квадратичной функции –
функций у = ах2 + b, y = a (x – m)2;
• научить строить графики квадратичной
функции.
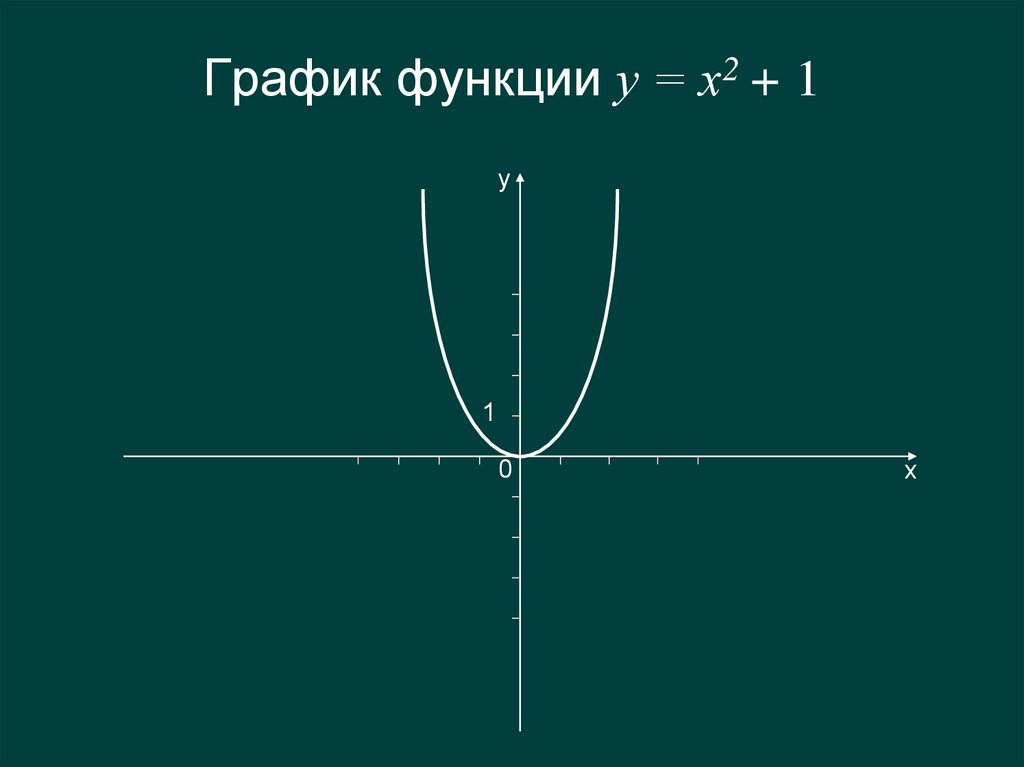
3. График функции у = х2 + 1
у1
0
х
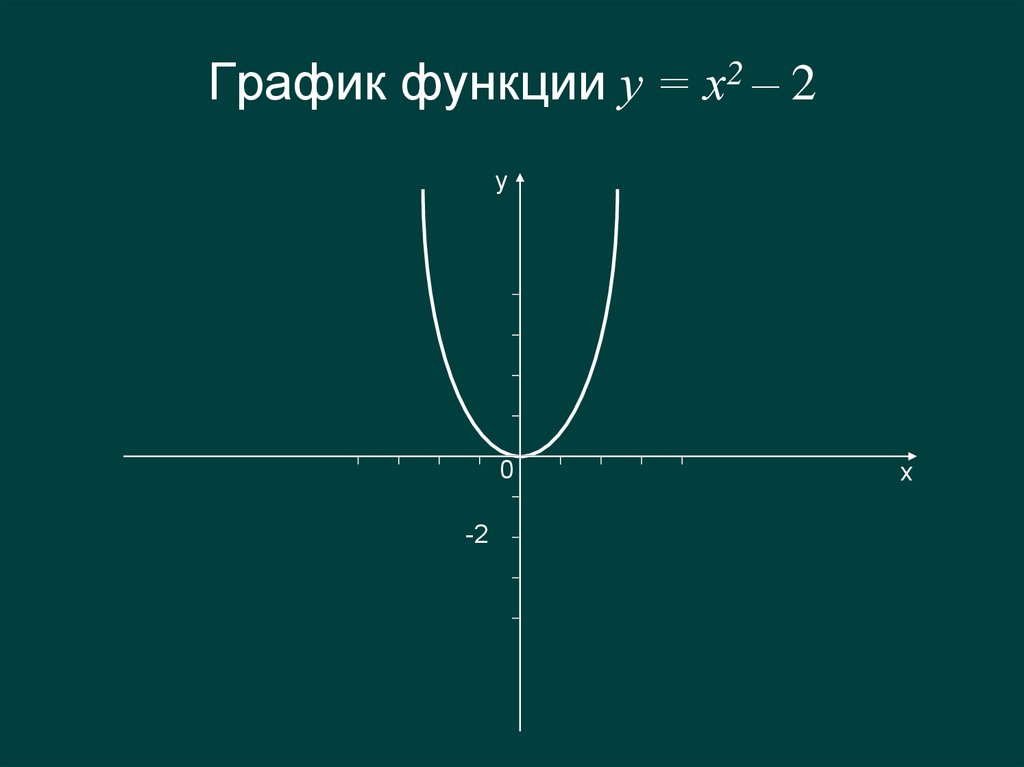
4. График функции у = х2 – 2
у0
-2
х
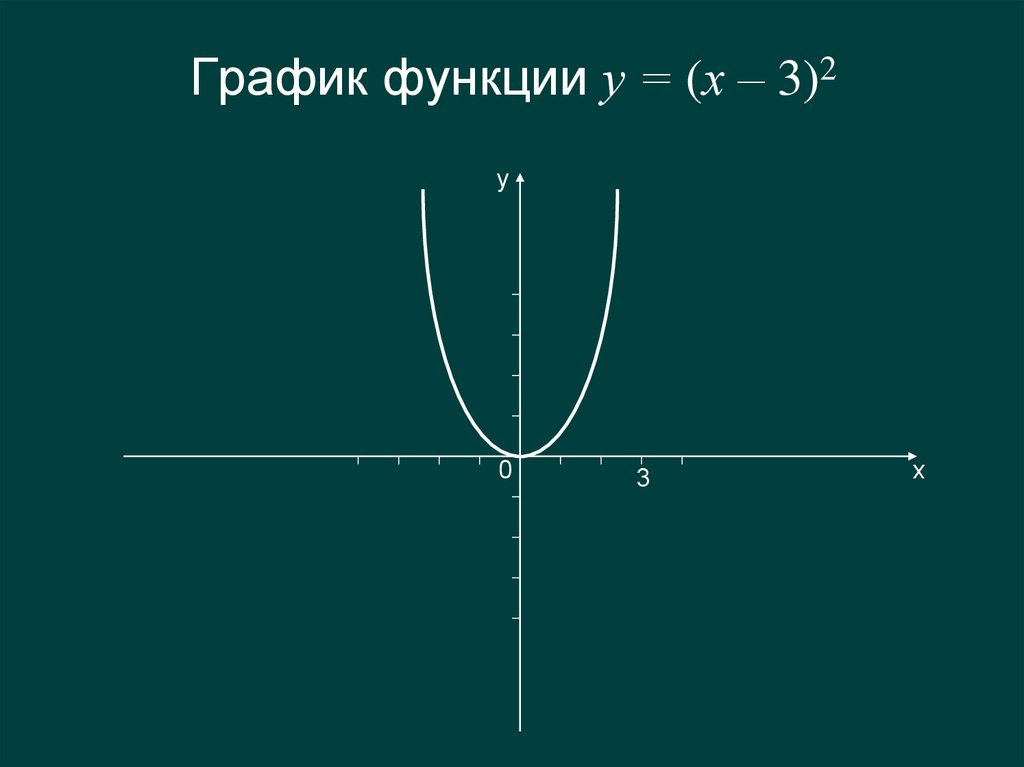
5. График функции у = (х – 3)2
у0
3
х
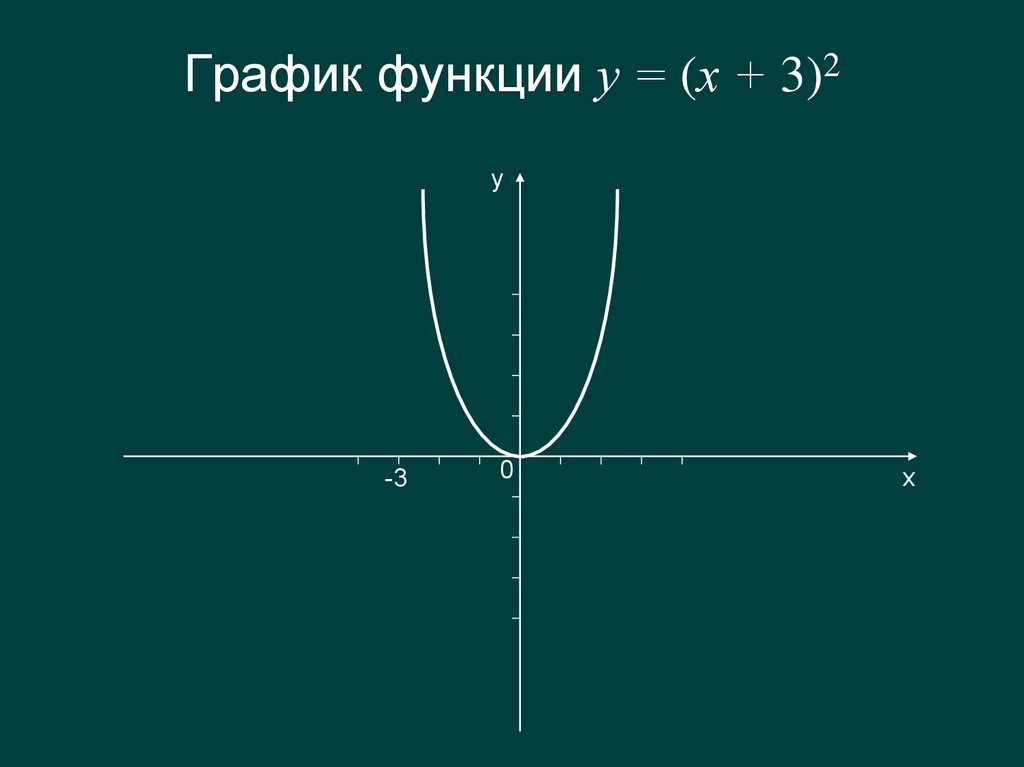
6. График функции у = (х + 3)2
у-3
0
х
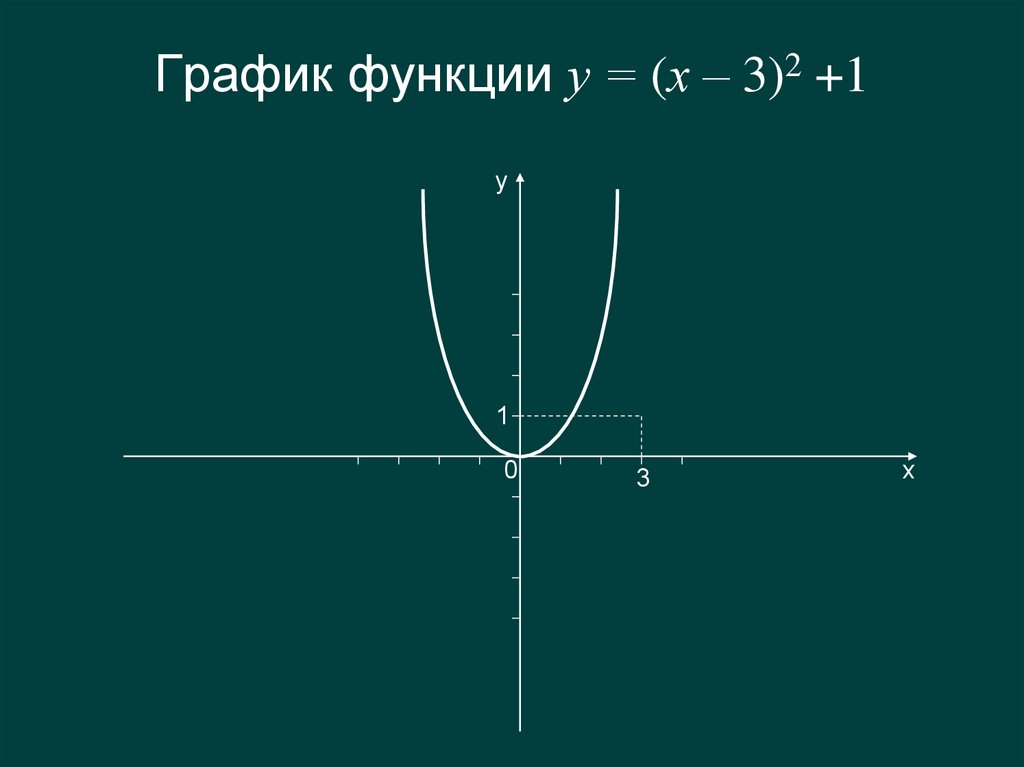
7. График функции у = (х – 3)2 +1
у1
0
3
х
8. График функции у = (х + 3)2 – 2
у-3
х
0
-2
9. Итог урока
Как из графика функции у = ах2 можнополучить у = ах2 + n?
-График функции у = ах2 + n является
параболой, которую можно получить
из графика функции у = ах2 с помощью
параллельного переноса вдоль оси у
на n единиц вверх, если n >0,
или на - n единиц вниз, если n < 0.
10. Итог урока
Как из графика функции у = ах2 можнополучить у = а(х – т)2 ?
- График функции у = а(х – т)2 является
параболой, которую можно получить из
графика функции у = ах2 с помощью
параллельного переноса вдоль
оси х на т единиц вправо, если m > 0,
или на - т единиц влево, если m < 0.
11. Итог урока
Как из графика функции у = ах2 можнополучить у = а(х – m)2 + n?
-График функции у = а(х – m)2 + n является
параболой, которую можно получить из графика
функции у = ах2 с помощью двух параллельных
переносов: сдвига вдоль оси х на т единиц
вправо, если m > 0, или на - т единиц влево,
если m < 0, и сдвига вдоль оси у на n единиц
вверх, если n >0, или на - n единиц вниз,
если n < 0.
12. Задание на дом
п. 6, № 106 (б,г),№ 107 (б),
№ 110 (а,г),
№ 117 (б)






 Математика
Математика








