Множеств, подмножество, пустое множество

1.

Множества

2.

Сегодня на уроке мы…
• узнаем, что такое множество, подмножество,
пустое множество;
• изучим обозначения для геометрической
иллюстрации множеств;
• научимся приводить примеры множества, решать
предложенные задачи с использованием кругов
Эйлера, выделять из множества подмножество.

3.

Вспомним
В каких случаях составное высказывание А И В
может быть истинным?
Составное высказывание А и В, образованное в
результате объединения двух простых
высказываний А и B логической операцией И,
истинно тогда и только тогда, когда А и В
одновременно истинны.

4.

Вспомним
В каких случаях составное высказывание А ИЛИ В
может быть ложным?
Составное высказывание А ИЛИ В, образованное
в результате объединения двух высказываний
А и B логической операцией ИЛИ, ложно тогда и
только тогда, когда А и В одновременно ложны.

5.

Понятие множества

6.

Рассмотрим высказывание
«Все учащиеся нашего класса имеют дома
компьютер».
Истинно оно или ложно?

7.

Зададим каждому однокласснику
вопрос
«У тебя дома есть компьютер?».

8.

Если все учащиеся класса ответят утвердительно, то
высказывание истинно, если хотя бы один из учащихся
ответит «нет», то и высказывание будет ложным. Для
разных классов это высказывание будет иметь различные
значения, потому что различными будут множества
учащихся класса.

9.

Множества, в том числе и бесконечные, в
неявной форме использовались в
математике со времен Древней Греции.
До XIX в. считалось, что точного
определения множества нет.
Множеством называли любое скопление,
объединение предметов.
В конце XIX в. немецкий математик
Георг Кантор (1845—1918) определил
множество как «единое имя для
совокупности всех объектов,
обладающих данным свойством»

10.

Множество — совокупность какихлибо объектов, обладающих общим
свойством. Эти объекты называют
элементами множества.

11.

Можно говорить о множестве:
• учащихся 7 А класса,
• отметок в классном журнале,
• городов Беларуси,
• букв русского алфавита и т. д.
Понятие множества является одним из основных в
математике.

12.

Множества, как правило, обозначают прописными
латинскими буквами, а элементы множества —
строчными.
Для обозначения принадлежности элемента множеству
используют специальные знаки:
а ∈ М (элемент а принадлежит множеству М),
а ∉ М (элемент а не принадлежит множеству М).
Если множество M состоит из элементов a, b, c, то это
записывают так: M = {a, b, c}.

13.

Чтобы задать множество, необходимо перечислить его элементы
пример
Пусть множество M — это множество любимых учебных
предметов семиклассника Игоря, состоящее из следующих
элементов: математика, информатика, английский язык.
Тогда можно записать:
М = {математика, информатика, английский язык};
информатика ∈ М ;
литература ∉ М.

14.

или назвать их общее свойство
пример
Пусть в множество M входят все учебные предметы, которые
изучаются в 7-м классе. Перечислить все элементы данного
множества можно, например, глядя на страницу школьного
дневника.
Тогда можно записать:
информатика ∈ М ;
астрономия ∉ М .

15.

Понятие подмножества

16.

Рассмотрим множество учащихся какого-либо класса. В
этом множестве можно выделить не только отдельного
учащегося, но и некоторые группы учащихся.
Например, отличники, учащиеся, умеющие играть в
теннис, изучающие французский язык и т. д. Каждая из
таких групп образует подмножество — часть
множества учащихся.

17.

Если множество А является подмножеством
множества М, то это записывают так: А ⊂ М.
Запись А ⊄ М обозначает, что множество А не
является подмножеством множества М.
Подмножество может содержать все элементы
множества, а может не содержать ни одного (пустое
множество; обозначается знаком ∅).

18.

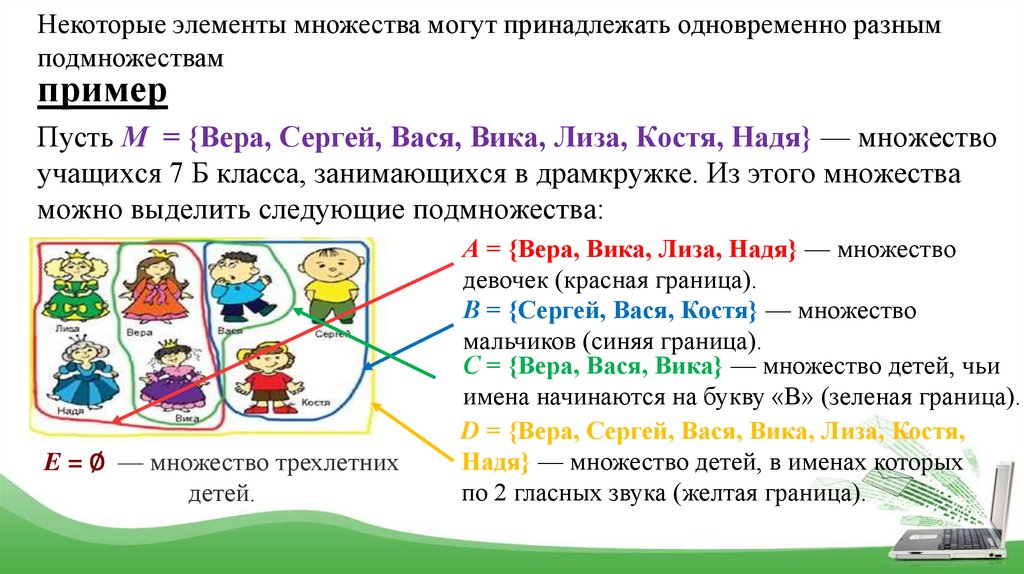
Некоторые элементы множества могут принадлежать одновременно разным
подмножествам
пример
Пусть М = {Вера, Сергей, Вася, Вика, Лиза, Костя, Надя} — множество
учащихся 7 Б класса, занимающихся в драмкружке. Из этого множества
можно выделить следующие подмножества:
E = ∅ — множество трехлетних
детей.
А = {Вера, Вика, Лиза, Надя} — множество
девочек (красная граница).
В = {Сергей, Вася, Костя} — множество
мальчиков (синяя граница).
С = {Вера, Вася, Вика} — множество детей, чьи
имена начинаются на букву «В» (зеленая граница).
D = {Вера, Сергей, Вася, Вика, Лиза, Костя,
Надя} — множество детей, в именах которых
по 2 гласных звука (желтая граница).

19.

Для наглядной геометрической иллюстрации множеств и
отношений между ними используют круги Эйлера.
Каждое множество изображается кругом.
Если какое-либо множество является подмножеством
другого множества, то один круг изображается внутри
другого.

20.

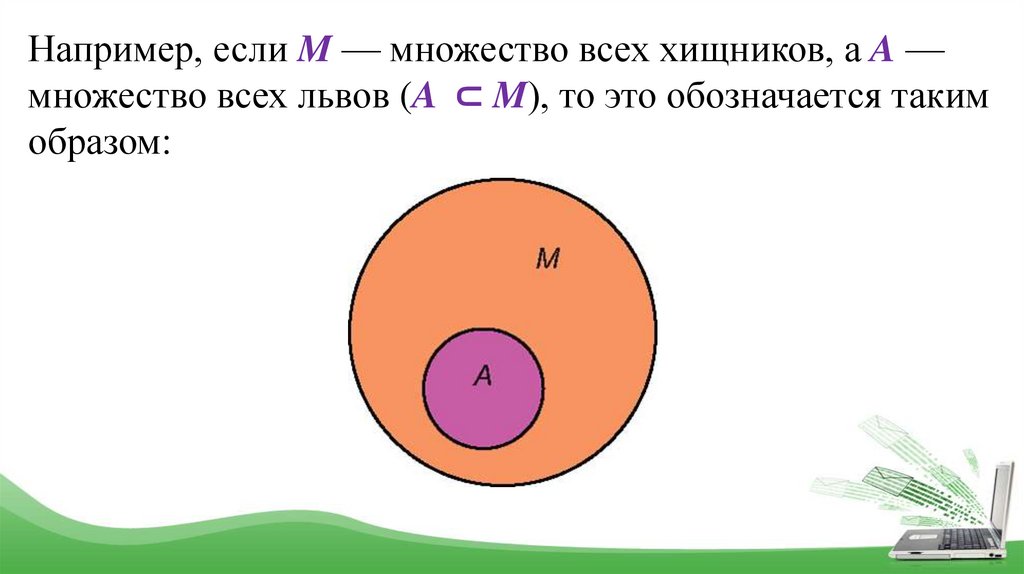
Например, если M — множество всех хищников, а A —
множество всех львов (A ⊂ M), то это обозначается таким
образом:

21.

Упражнения

22.

Какие элементы могут входить в следующие множества?
1) Средства передвижения;
2) цвета радуги;
3) домашние животные;
4) четные числа.

23.

Дополните каждое из множеств 1—2 элементами.
1) А = {математика, информатика, история, литература};
2) В = {яблоко, груша, апельсин, банан};
3) С = {клавиатура, монитор, мышь};
4) D = {карандаш, ручка, ластик, фломастер}.

24.

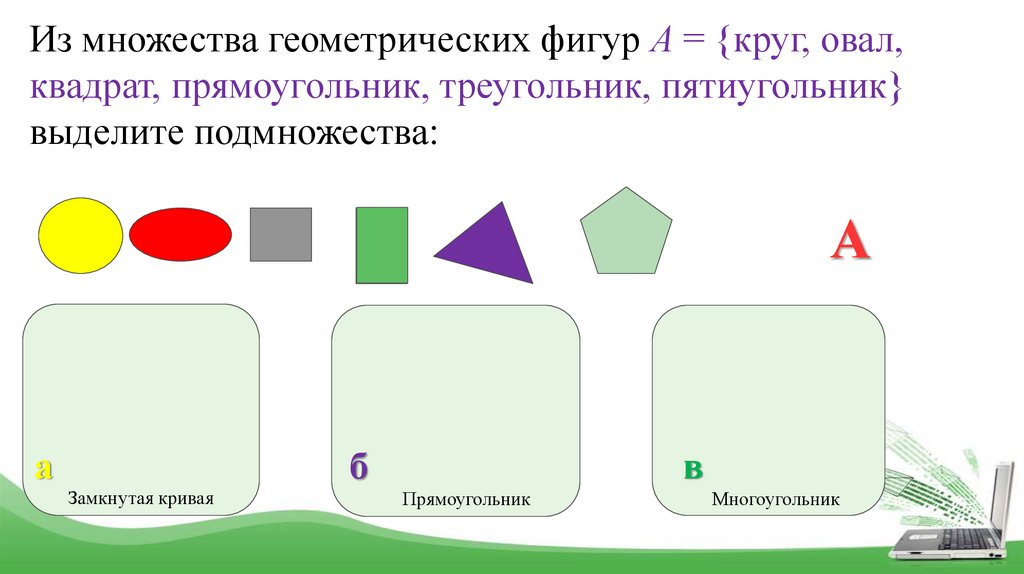
Из множества геометрических фигур А = {круг, овал,
квадрат, прямоугольник, треугольник, пятиугольник}
выделите подмножества:
А
а
в
б
Замкнутая кривая
Прямоугольник
Многоугольник

25.

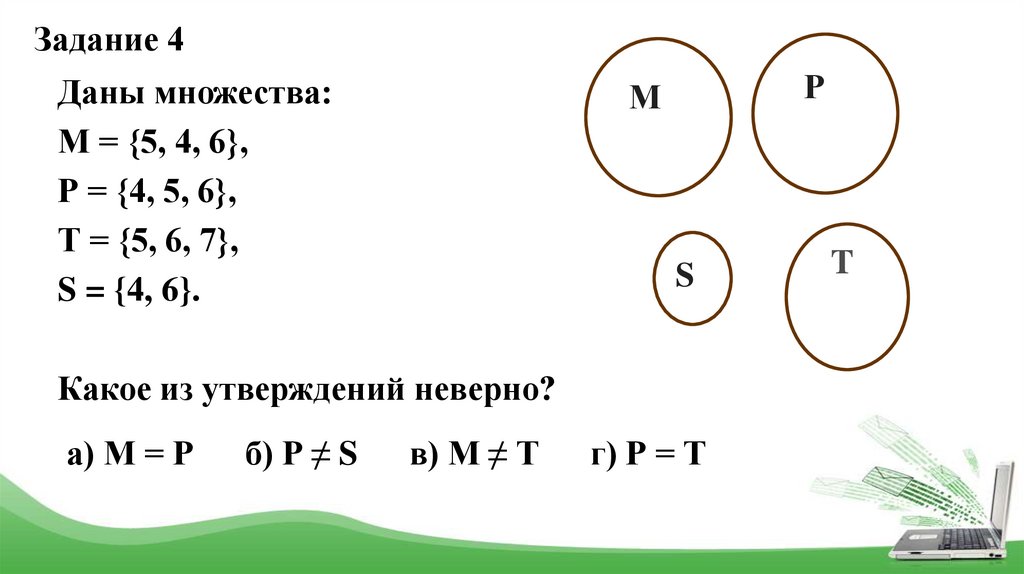
Задание 4
Даны множества:
М = {5, 4, 6},
Р = {4, 5, 6},
Т = {5, 6, 7},
S = {4, 6}.
Р
М
S
Какое из утверждений неверно?
а) М = Р
б) Р ≠ S
в) М ≠ Т
г) Р = Т
T

26.

Повторим
Что понимают под множеством?
Множество — совокупность каких-либо объектов,
обладающих общим свойством. Эти объекты
называют элементами множества.

27.

Повторим
Приведите примеры множеств
• множество книг в библиотеке;
• множество автомобилей на стоянке;
• множество звёзд на небосводе;
• растительный и животный мир Земли

28.

Повторим
Что понимают под подмножеством?
Подмножество — часть множества.
Множество А называется подмножеством
множества B, если все элементы,
принадлежащие А также принадлежат В

29.

Повторим
Что используется для геометрической иллюстрации
множеств?
Для наглядной геометрической
иллюстрации множеств и отношений
между ними используют круги Эйлера.
Каждое множество изображается кругом.
Если какое-либо множество является
подмножеством другого множества, то
один круг изображается внутри другого.

30.

Повторим
Что понимают под пустым множеством? Как оно
обозначается?
Пустое множество — множество, не содержащее
ни одного элемента.
Пустое множество обозначается знаком ∅

31.

Повторим
Может ли элемент множества одновременно
принадлежать различным подмножествам?
Некоторые элементы
множества могут
принадлежать одновременно
разным подмножествам.

32.

Домашнее задание
§5