Специальные методы. Метод накопления

1.

3.2 Специальные методы
3.2.1 Метод накопления
В алгоритмических языках переменная может
изменять свое значение в течение времени.
Поэтому используют такие понятия,
«старое» и «новое» значение переменной.
как

2.

Пример 5. Найти сумму элементов массива.
1 Постановка задачи
1.1 Исходные данные
n: целое;
x: массив [1..n]: вещественных;
1.2 Ограничения
n>1
1.3 Результаты
S: вещественное;

3.

1.4 Связь
S = x1 + x2 + x3 + ... + xn
2 Метод
S = S + xi
для i = 1..n
S=0
Промежуточные данные
i: целое;
Если в методе требуются вспомогательные
переменные, их описывают после метода в том
же синтаксисе, что и исходные данные.

4.

Пример 6. Найти произведение элементов
массива.
1 Постановка задачи
1.1 Исходные данные
n: целое;
x: массив [1..n]: вещественных;
1.2 Ограничения
n>1
1.3 Результаты
P: вещественное;

5.

1.4 Связь
P = x1 * x2 * x3 * ... * xn
2 Метод
P = P * xi
для i = 1..n
P=1
Промежуточные данные
i: целое;

6.

3.2.2 Метод перебора
Пример 7. Найти количество положительных
элементов массива.
1 Постановка задачи
1.1 Исходные данные
n: целое;
x: массив [1..n]: вещественных;
1.2 Ограничения
n>1
1.3 Результаты
K: целое;

7.

1.4 Связь
K = количество ( x i > 0), i = 1..n
2 Метод
K = K + 1 при xi > 0
для i = 1..n
K=0
Промежуточные данные
i: целое;

8.

Пример 8. Найти минимум и его номер.
1 Постановка задачи
1.1 Исходные данные
n: целое;
x: массив [1..n]: вещественных;
1.2 Ограничения
n>1
1.3 Результаты
min: вещественное;
num: целое

9.

1.4 Связь
min = минимум (xi) , i = 1..n;
num = номер (min);
2 Метод
min = xi
num = i
при xi < min
для i = 2..n
min = x1
num=1
Промежуточные данные
i: целое;

10.

Рассмотренный
алгоритм
местоположение первого среди
минимальных элементов массива.
находит
нескольких
Чтобы найти местоположение последнего
среди одинаковых минимальных элементов
массива, нужно иначе записать условие:
ai <= min

11.

3.2.3 Метод последовательных приближений
Пример 9. Вычислить y = ex по формуле
x x2
x3
xn
y =1+ +
+
+ ... +
1!
2!
3!
n!
с заданной точностью.
1 Постановка задачи
1.1 Исходные данные
x: вещественное; {аргумент}
: вещественное; {точность}
1.2 Ограничения
>0
1.3 Результаты
y: вещественное;

12.

1.4 Связь
x x2
x3
xn
y =1+ +
+
+ ... +
1!
2!
3!
n!
Если
n x i n -1 x i
n -1 x i
∑
- ∑
< ξ , то y = ∑
; n = 1,2,3...
i =1 i! i =1 i!
i =1 i!
≡
n -1 x i
xn
< ξ , то y = ∑
; n = 1,2,3...
n!
i =1 i!
n xi
Можно также как резулььат брать y = ∑
i =1 i!

13.

2 Метод
i = i +1
xi
y = y+
i!
y =1
i =1
xi
пока
>= ξ
i!
Операция факториал (!) недоступна, заменяем
умножением:
n=n*i
i=i+1
где n – факториал, i – аргумент.

14.

Объединяем оба метода
n = n*i
i = i +1
S
S = S * x пока >= ξ
n
S
y = y+
n
y =1
n =1
s=x
i =1

15.

Промежуточные данные
S: вещественное {i-ая степень x}
n: целое {факториал}
i: целое {номер итерации}

16.

При
решении
подобных
использовать массивы:
задач
нельзя
1) Мы не можем заранее знать количество
членов в этой последовательности.
2) Нет необходимости хранить все m членов
этой последовательности, а достаточно
иметь два соседних элемента (текущий и
следующий или текущий и предыдущий).
3) При
переходе
к
следующему
шагу
повторяющихся
вычислений
текущее
значение делают предыдущим и вычисляют
новое текущее значение.

17.

4. Разработка алгоритмов
Алгоритм – это последовательность действий,
которые преобразуют исходные данные в
результаты.
Свойства алгоритма:
─ дискретность;
─ результативность (направленность);
─ массовость;
─ конечность (финитивность);
─ определенность (определенность, точность,
однозначность);
─ корректность.

18.

Дискретность – алгоритм состоит из
последовательности
отдельных
шагов
(элементарных действий), выполнение которых
не представляет сложности.
Следовательно,
алгоритм
реализован на ЭВМ.
может
быть
Результативность – выполнение алгоритма
обязательно должно привести к решению
поставленной задачи, либо к сообщению о том,
что при заданных исходных величинах задачу
решить невозможно.
Алгоритмический
процесс
обрываться безрезультатно.
не
может

19.

Массовость – с помощью алгоритма можно
решать не одну конкретную задачу, а любую
задачу из некоторого класса однотипных задач
при всех допустимых значениях исходных
данных.
Конечность
–
последовательность
элементарных действий алгоритма не может
быть бесконечной, неограниченной, хотя может
быть очень большой (если требуется,
например, большая точность вычислений).

20.

Определенность – при задании одних и тех же
исходных данных несколько раз алгоритм будет
выполняться абсолютно одинаково и всегда
будет получен один и тот же результат.
На каждом шаге выполнения алгоритма всегда
точно известно, что делать дальше, а каждое
действие однозначно понятно исполнителю и не
может быть истолковано неопределенно.
Благодаря
этому
свойству
выполнение
алгоритма носит механический характер.

21.

Корректность – если алгоритм создан для
решения определенной задачи, то для всех
исходных данных он должен всегда давать
правильный результат и ни для каких исходных
данных не будет получен неправильный
результат.
Если хотя бы один из полученных результатов
противоречит хотя бы одному из ранее
установленных
и
получивших
признание
фактов, алгоритм нельзя признать корректным.
Выделяют несколько степеней корректности
алгоритма.

22.

Для записи алгоритма используют такие языки:
1. Вербальный (на естественном языке);
2. Символьный
(псевдокод:
учебный
алгоритмический язык Ершова и др.);
3. Графические (блок (граф)-схемы, ДРАКОНсхемы).
Мы будем рассматривать графический язык
блок-схем.

23.

Алгоритм отличается от метода тем, что кроме
трех
конструкций
структурного
программирования
(последовательность,
ветвление и повторение) в алгоритме будут
операторы ввода и вывода.
В
алгоритме
обязательно
ограничения на исходные данные!
проверяют

24.

Базовые операторы:
1. Ввод исходных данных
a, b, c
2. Вычисление значений
y := <выражение>
3. Вызов подпрограммы
y := <имя_подпр-мы>
(<список_аргументов>)
<имя_подпр-мы>
(<список_аргументов>)

25.

4. Вывод результатов
"x1=", x1
"x2=", x2
Алгоритм
последовательно
исходные данные в результаты.
преобразует
Если он не может это сделать непосредственно,
то он использует промежуточные вычисления,
которые хранятся в промежуточных данных.

26.

5. Условный оператор
+
<условие>
<действие 1>
+
<действие 1>
-
<действие 2>
<условие>
-

27.

Условный оператор выполняется так:
1) Вычисляется значение условия.
2) Если оно равно "истина", то выполняются
операторы ветки "то" и переход на оператор,
следующий за условным.
3) Если условие равно "ложь", то выполняются
операторы ветки "иначе" (если она есть) и
переход на оператор, следующий за
условным.

28.

6. Оператор цикла
Цикл с известным числом повторений:
i := 1 .. n, <шаг>
<тело_цикла>
Если шаг отсутствует, то он по умолчанию
равен +1

29.

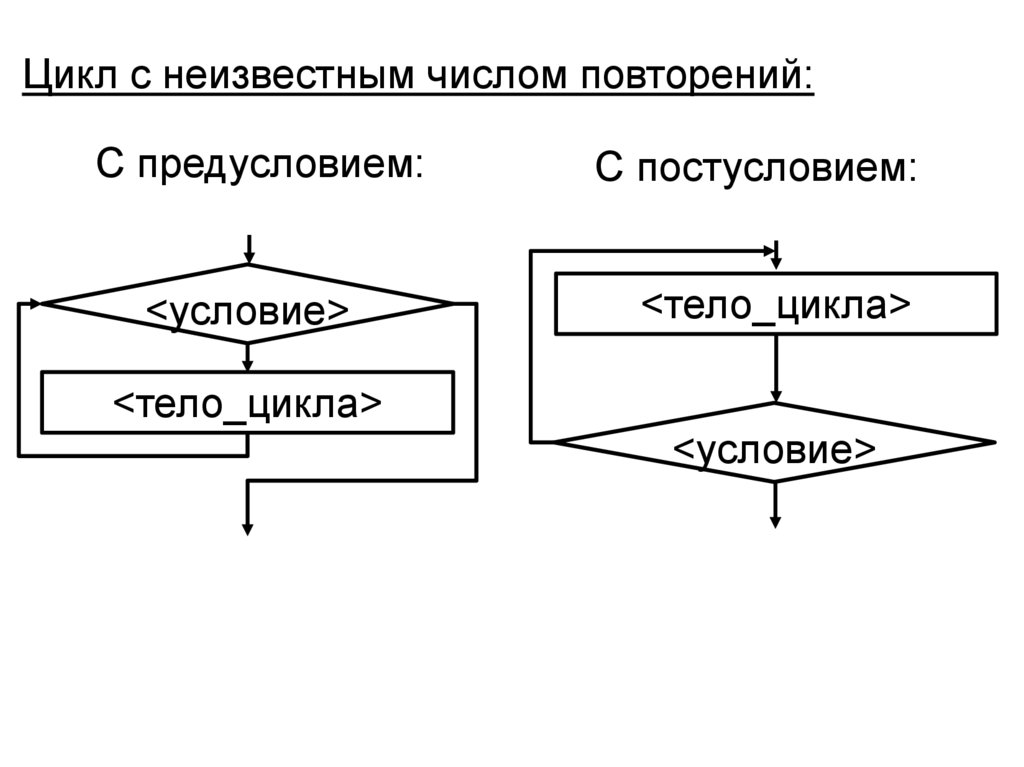
Цикл с неизвестным числом повторений:
С предусловием:
С постусловием:
<условие>
<тело_цикла>
<тело_цикла>
<условие>

30.

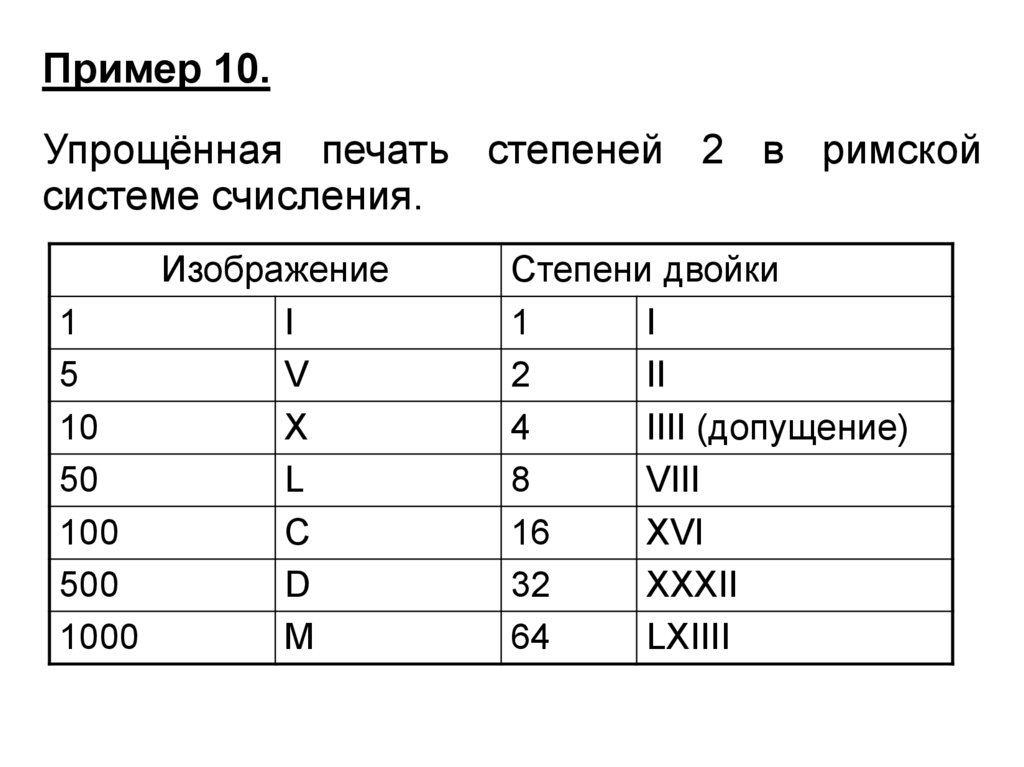
Пример 10.
Упрощённая печать степеней 2 в римской
системе счисления.
Изображение
1
I
5
V
10
X
50
L
100
C
500
D
1000
M
Степени двойки
1
I
2
II
4
IIII (допущение)
8
VIII
16
XVI
32
XXXII
64
LXIIII

31.

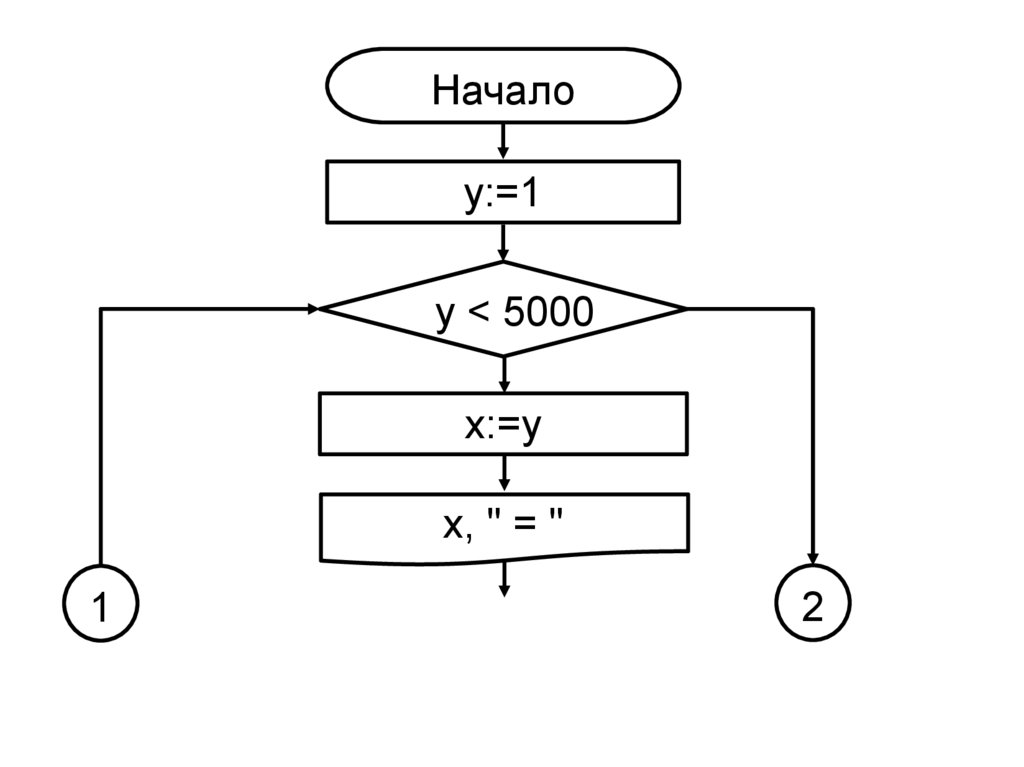
Начало
y:=1
y < 5000
x:=y
x, " = "
1
2

32.

x >= 1000
'M'
x:=x-1000
x >= 500
+
'D'
x:=x-500
-

33.

x >= 100
'C'
x:=x-100
x >= 50
+
'L'
x:=x-50
-

34.

x >= 10
'X'
x:=x-10
-
x >= 5
+
'V'
x:=x-5

35.

1
2
x >= 1
'I'
x:=x-1
y:=y*2
Конец

36.

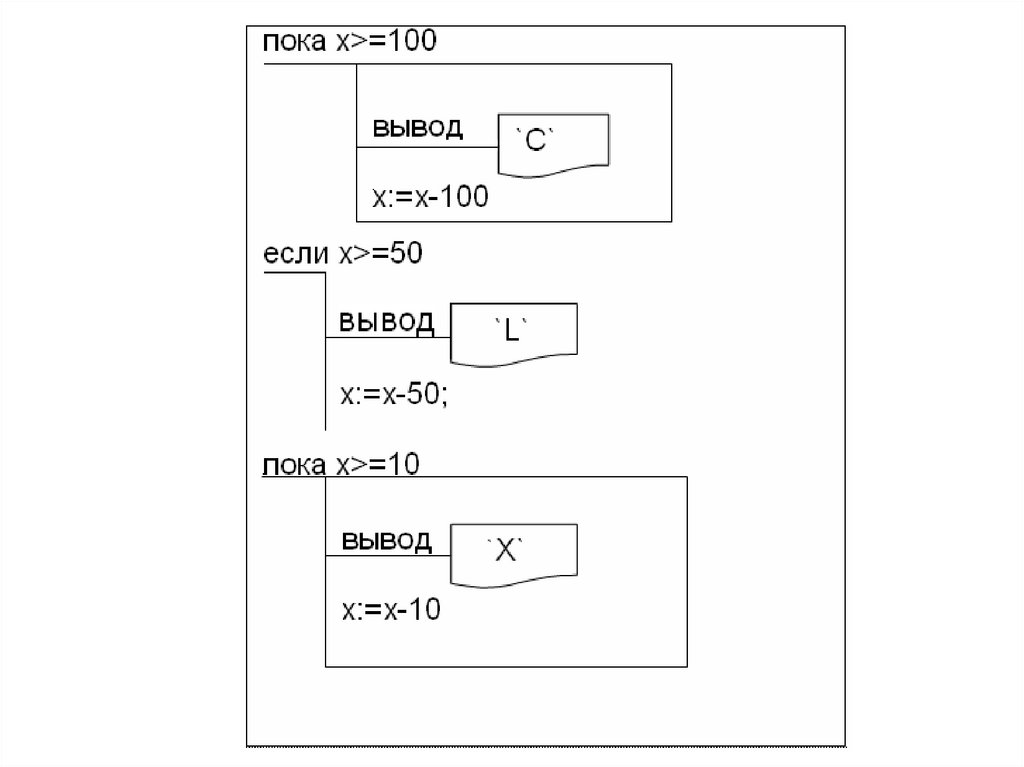
Альтернативная графическая запись алгоритма

37.

38.

39.

40.

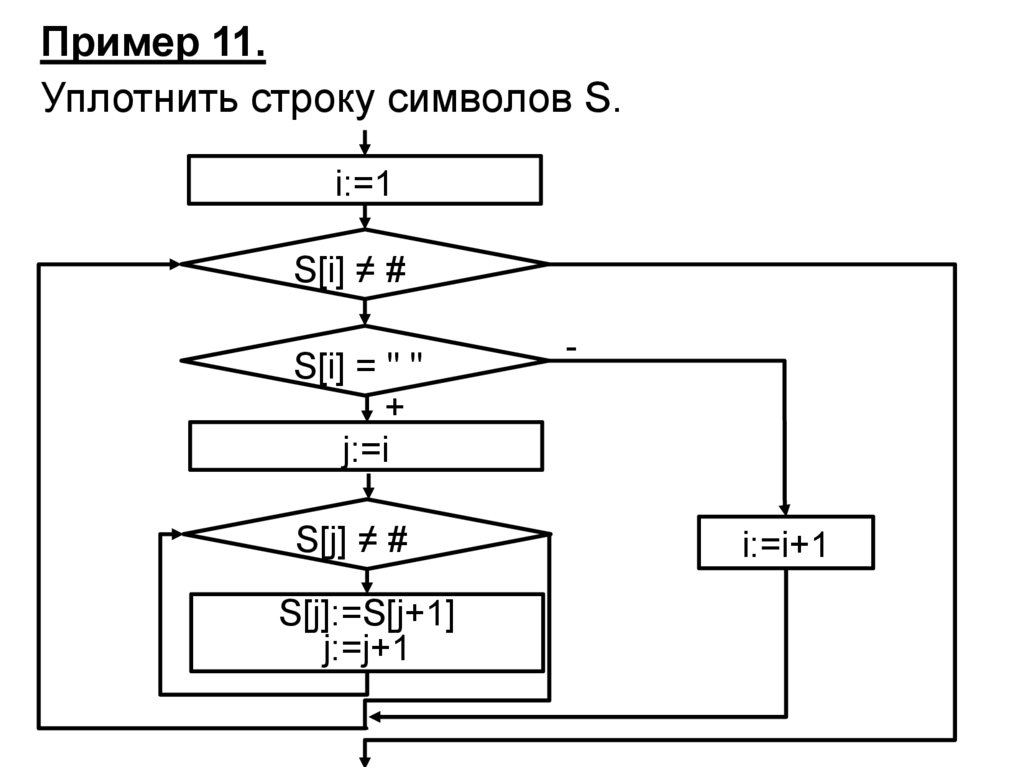
Пример 11.
Уплотнить строку символов S.
i:=1
S[i] ≠ #
S[i] = " "
+
j:=i
S[j] ≠ #
S[j]:=S[j+1]
j:=j+1
-
i:=i+1