Похожие презентации:
Занятие №5. Анализ сглаживания параметров линейной траектории по фиксированной выборке измеренных координат
1.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙУНИВЕРСИТЕТ
Военный учебный центр
ОСНОВЫ ОБРАБОТКИ И ПЕРЕДАЧИ
ИНФОРМАЦИИ В АСУ
Тема № 2. Автоматизация вторичной
обработки РЛИ
Занятие № 5. Анализ сглаживания параметров
линейной траектории по фиксированной выборке
измеренных координат
Руководитель занятия:
доцент кафедры АСУ ВКС
капитан Тяпкин И.В.
2.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТУчебные вопросы:
1. Физический
смысл
операции
весового
суммирования измеренных координат.
2. Показатель
качества
сглаживания
и
экстраполяции.
3. Расчет значений
сглаживающей
функции
алгоритма оптимальной оценки параметров
линейной траектории.
4. Синтез
структурной
схемы
решающего
устройства для оптимальной оценки параметров
ЛО.
2
3.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТЛитература
1. В.Н. Ратушняк, С.В. Бейльман, И.В. Тяпкин. Основы
обработки
и
передачи
информации
в
автоматизированных системах управления. Часть II
Вторичная обработка радиолокационной информации.
– Красноярск: СФУ ВУЦ, 2021 – С. 67 - 83.
2. Справочник офицера воздушно-космической обороны /
под. ред. С.К. Бурмистрова. – Тверь: ВА ВКО, 2008. –
С.523–527.
3
4.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВопрос №1
Физический смысл операции
весового суммирования измеренных
координат.
4
5.
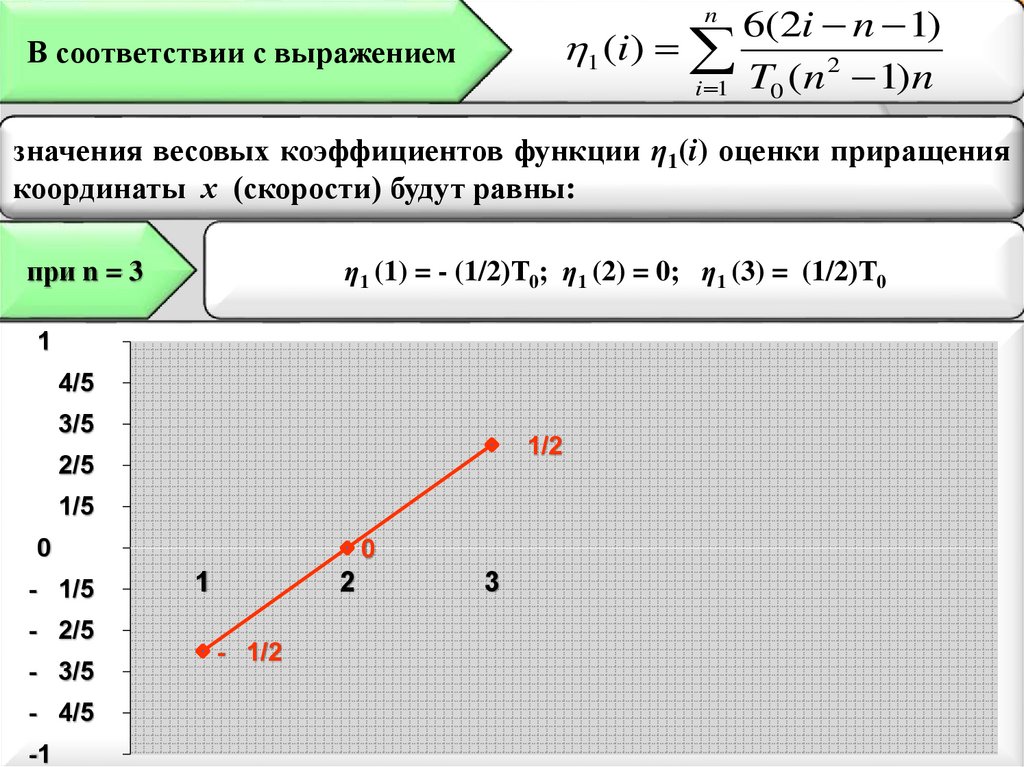
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВначале обратим внимание на характер весовых коэффициентов
сглаживания.
Анализ сглаживания проводился для параметров равномерного
движения.
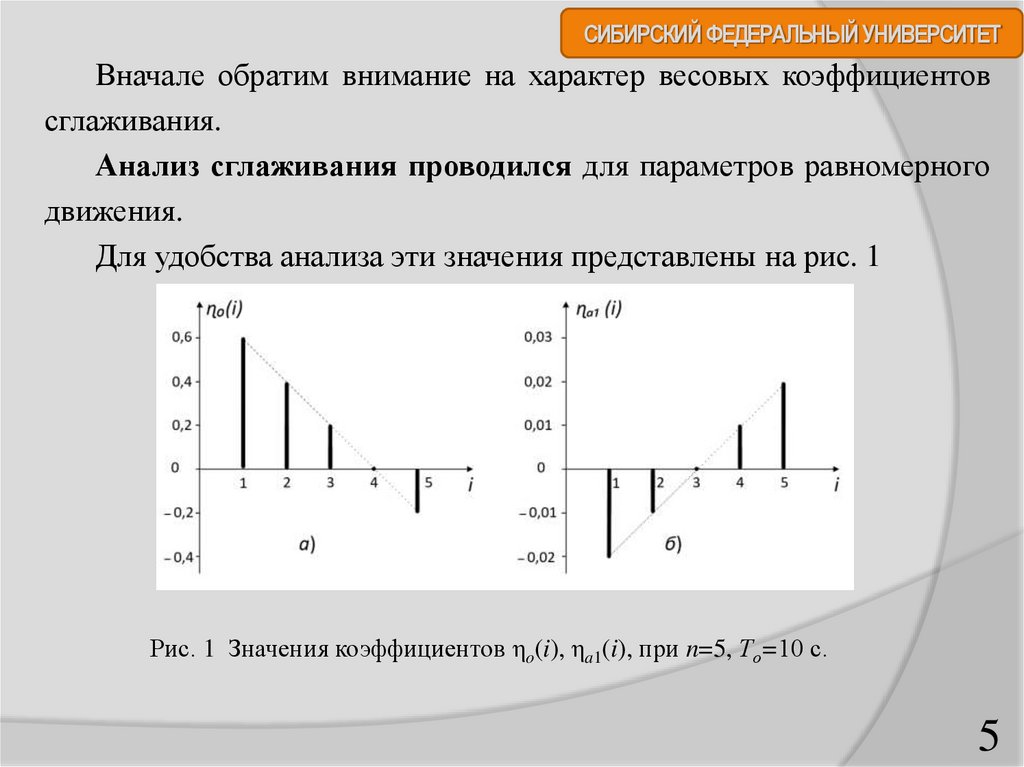
Для удобства анализа эти значения представлены на рис. 1
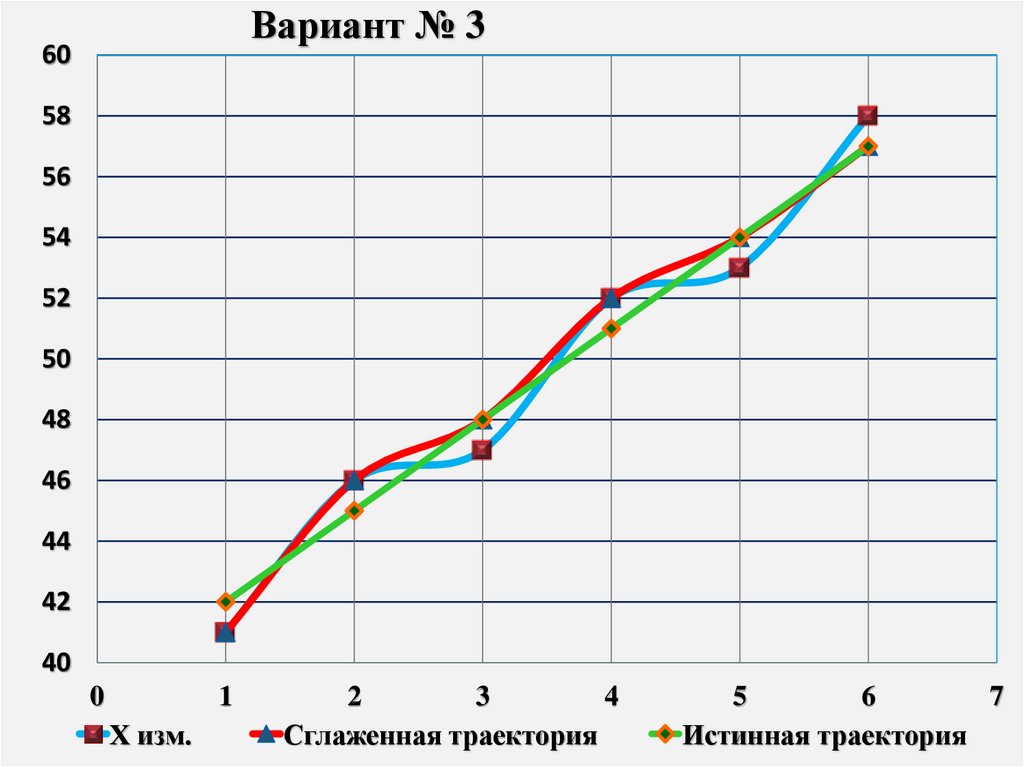
Рис. 1 Значения коэффициентов ηo(i), ηa1(i), при n=5, То=10 с.
5
6.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТКак следует из рис. 1, весовые коэффициенты ηo(i), ηa1(i) линейно зависят
от порядкового номера измерения (от переменной i).
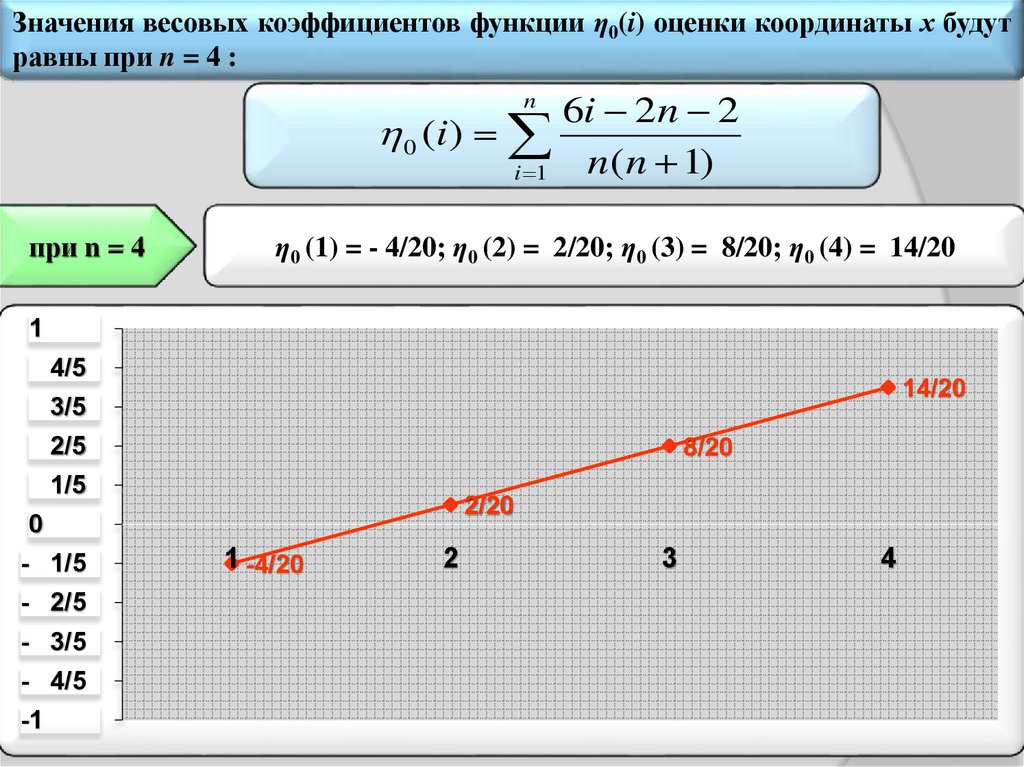
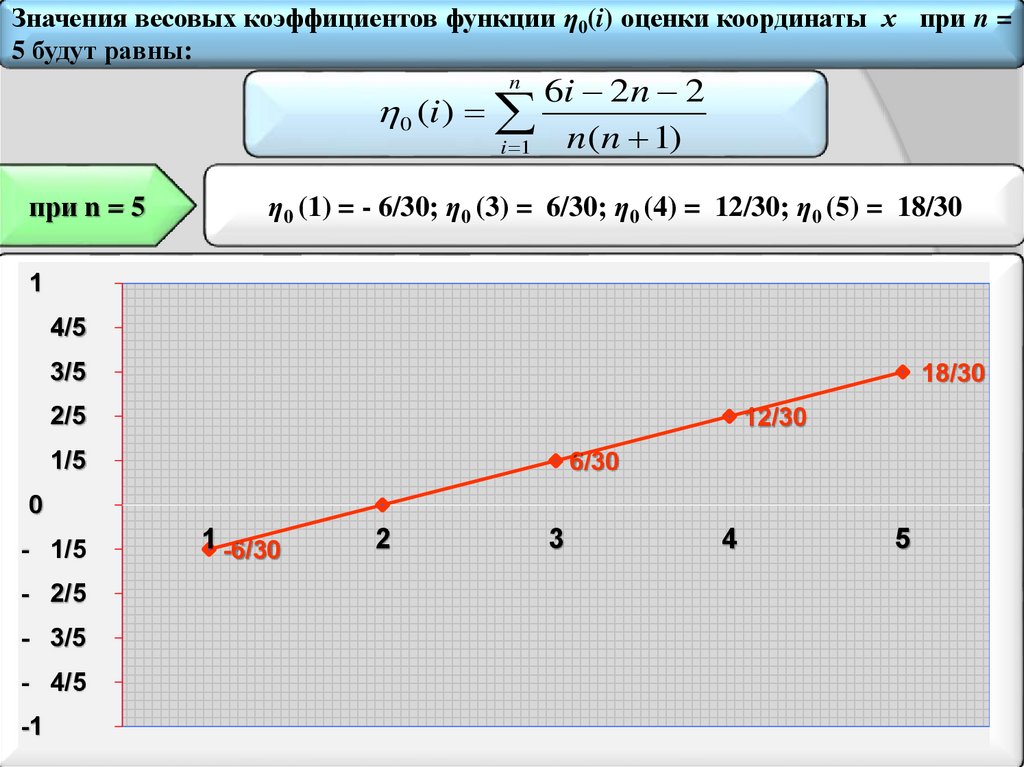
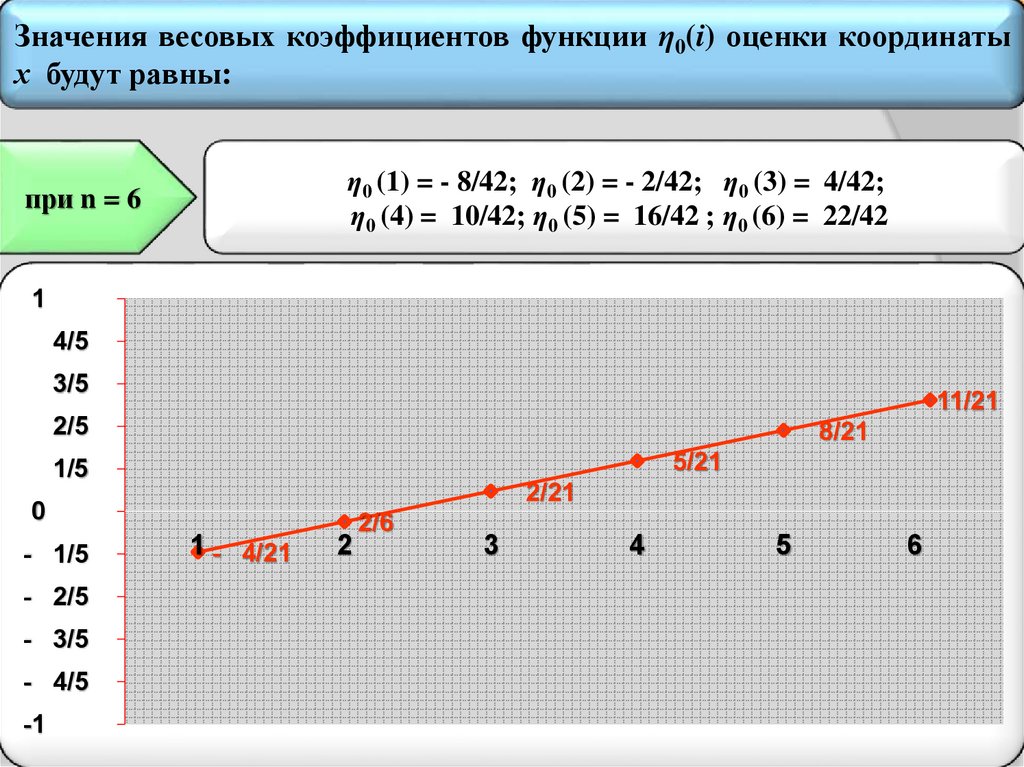
Весовые коэффициенты ηo(i), используемые для оценки параметра aо
(начальной координаты траекторий), при изменении i от единицы до 2n/3
принимают положительные значения, а для остальных i ‒ отрицательные,
включая ноль. Алгебраическая сумма весовых коэффициентов ηo(i) при
любых значениях n равна единице. Весовые коэффициенты ηa1(i),
используемые для оценки параметра а1 (скорости), попарно симметричны:
ηa1(1)= ηa1(n); ηa1(2)= ηa1(n 1). Поэтому алгебраическая сумма весовых
коэффициентов ηa1(i) при любых значениях n равна нулю.
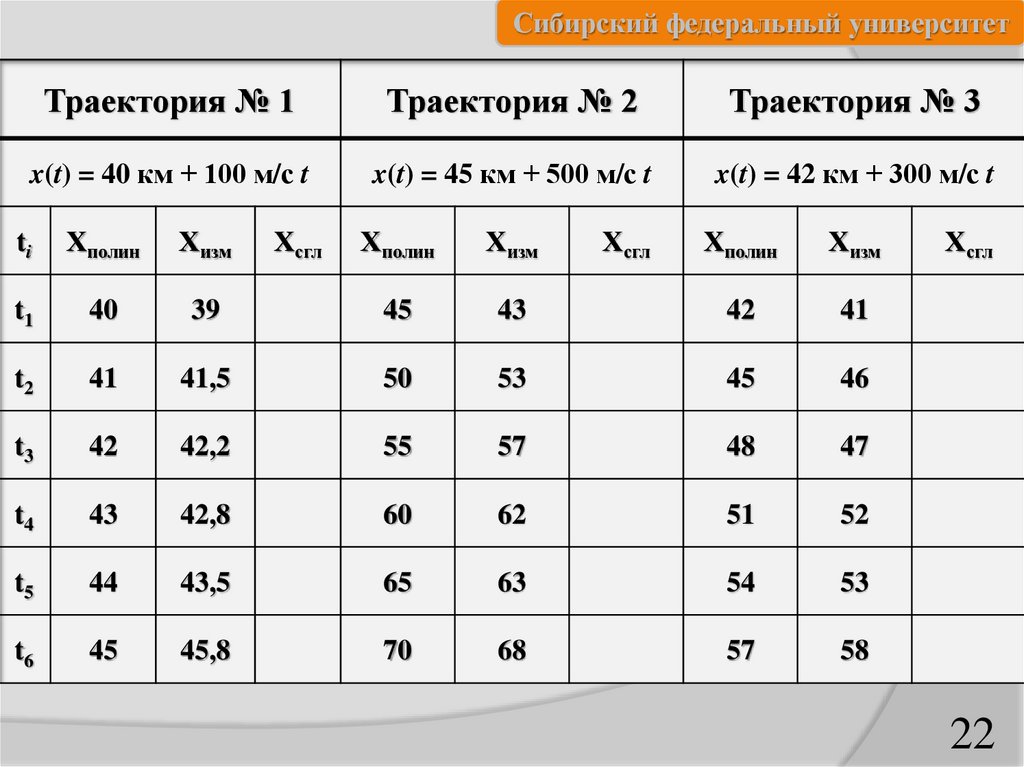
Допустим, что после пяти измерений получена выборка координат X=||X1
X2 X3 X4 X5||. Каждая из измеренных координат содержит ее истинное значение
X(a,ti) и погрешность измерения δX, т. е.
X 1 X a, t1 X 1 ao X 1;
X 2 X a, t2 X 2 ao a1To X 2 ;
. . . . . . . . . . . . . . . . . . .
X 5 X a, t5 X 5 ao 4a1To X 5 .
6
7.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТСогласно приведенным соотношениям, измеренная координата
содержит три составляющие ‒ истинные параметры траектории а0, а1
и погрешность измерения δXi:
X i ao i 1 a1To X i .
(1)
Учитывая свойства весовых коэффициентов, выявим «механизм»
оценивания параметров а0, а1 по фиксированной выборке
измеренных координат Xi представленных выражением (1).
Подстановка выражения (1) позволяет записать cглаженное
значение параметра а0 в виде трех весовых сумм:
n
n
n
n
i 1
i 1
i 1
i 1
a o o i X i o i ao o i a1 i 1 To o i X i .
Первая сумма определяет оценку начальной координаты
траектории, равную истинному значению параметра а0:




























 Информатика
Информатика Военное дело
Военное дело








