Похожие презентации:
Квадратный трехчлен
1.
КВАДРАТНЫЙ ТРЕХЧЛЕН2.
Квадратным трёхчленом называетсямногочлен вида
ах² + bх + c,
где х - переменная, а, b и с некоторые
числа, причём а ≠0
3.
ах² + bх + c, а ≠02 х2-5х+4
8 х-5
16-х2-2х
х3-2 х2+2
х2-4х
6 х2
4.
ах² + bх + c, а ≠02 х2-5х+4
а =2 b = -5 с = 4
5.
ах² + bх + c, а ≠02 х2-5х+4
8 х-5
а =2 b = -5 с = 4
6.
ах² + bх + c, а ≠02 х2-5х+4
8 х-5
16- х2- 2х
а =2 b = -5 с = 4
а = -1 b = -2 с = 16
7.
ах² + bх + c, а ≠02 х2-5х+4
8 х-5
16- х2- 2х
х3-2 х2+2
а =2 b = -5 с = 4
а = -1 b = -2 с = 16
8.
ах² + bх + c, а ≠02 х2-5х+4
8 х-5
16- х2- 2х
х3-2 х2+2
х2 - 4х
а =2 b = -5 с = 4
а = -1 b = -2 с = 16
а=1 b=-4 с=0
9.
ах² + bх + c, а ≠02 х2-5х+4
8 х-5
16- х2- 2х
х3-2 х2+2
х2 - 4х
6 х2
а =2 b = -5 с = 4
а = -1 b = -2 с = 16
а=1 b=-4 с=0
а=6 b=0 с=0
10.
Левая часть квадратного2
уравнения ax +bx+c=0 является
квадратным трёхчленом
11.
Корнем квадратного трехчленаназывается значение переменной, при
котором значение квадратного
трехчлена равно нулю
5-корень квадратного
трёхчлена
х2 + 2х - 35
52 +2·5 - 35=0
12.
Для того, чтобы найти корниквадратного трёхчлена
ах2 + вх + с,
надо решить квадратное уравнение
ах2 + вх + с = 0
13.
ax2 + bx + c=014.
ax2 + bx + c = 015.
ax2+bx+c=016.
ax2+bx+c=017.
х2 – 7х + 10 = 0D=b2- 4аc = (-7)2 – 4· 1 · 10 = 9
D>0, 2 корня
x1=
=5
х2=
=2
18.
2х – 7х + 10 =
19.
х2 – 7х + 10 =х2 – 2х – 5х + 10 =
20.
х2 – 7х + 10 =х2 – 2х – 5х + 10 =
= (х2 – 2х) + (– 5х + 10) =
21.
х2 – 7х + 10 =х2 – 2х – 5х + 10 =
= (х2 – 2х) + (– 5х + 10) =
= х (х –2) – 5 (х –2) =
22.
х2 – 7х + 10 =х2 – 2х – 5х + 10 =
= (х2 – 2х) + (– 5х + 10) =
= х (х –2) – 5 (х –2) =
= (х –2) (х – 5)
23.
х2 – 7х + 10 =х2 – 2х – 5х + 10 =
= (х2 – 2х) + (– 5х + 10) =
= х (х –2) – 5 (х –2) =
(х –2) (х – 5)
24.
Если дискриминант квадратноготрехчлена ах² + bх + c положительный,
то данный трехчлен можно разложить
на линейные множители:
ах² + bх + c = а (х- х1 )(х - х2 ), где х1 и х2
корни квадратного трехчлена
25.
Если дискриминант квадратноготрехчлена ах² + bх + c равен нулю, то
данный трехчлен можно разложить на
линейные множители:
ах² + bх + c = а (х - х1 )², где х1 корень
квадратного трехчлена
26.
Если дискриминант квадратноготрехчлена ах² + bх + c
отрицательный, то данный
трехчлен нельзя разложить на
линейные множители
27.
Разложение на множителиЧтобы разложить квадратный трехчлен
ax2+bx+c на множители, нужно:
1. Квадратный трехчлен приравнять к нулю
2. Найти корни квадратного уравнения
ax2+bx+c=0.
3. Разложить квадратный трехчлен на
множители по формуле:
ax2 + bx + c = a(x - x1)(x - x2)
28.
Разложение на множители2х2 – 5х + 8
2х2 – 5х + 8=0
D=b2 – 4аc=(– 5)2– 4·2· 8 =25 – 64=
– 39
D< 0, нет корней
29.
Разложение на множители2х2 – 5х + 8
2х2 – 5х + 8=0
D=b2 – 4аc=(– 5)2– 4·2· 8 =25 – 64= – 39
D< 0, нет корней
Квадратный трёхчлен 2х2 – 5х + 8
разложить на множители нельзя
30.
Разложение на множители4х2 + 28х + 49
4х2 + 28х + 49 = 0
D=b2 – 4аc=(– 28)2– 4·4· 49 =784 –
784= 0
D= 0, 1 корень
ах² + bх + c = а (х - х1 )², где
х1 корень квадратного трехчлена
31.
Разложение на множители4х2 + 28х + 49
4х2 + 28х + 49 = 0
D=b2 – 4аc=(– 28)2– 4·4· 49 =784 – 784= 0
D= 0, 1 корень
ах² + bх + c = а (х - х1 )², где х1 корень квадратного
трехчлена
х=
Квадратный трёхчлен
4х2 + 28х + 49 = 4 (х – (– 3,5)) 2 = 4 (х+3,5)2
32.
Разложение на множители– х2 + 17х – 30
2
– х + 17х – 30 = 0
D=b2 – 4аc=(17)2– 4· (– 1)· (– 30) =
= 289 – 120 = 169
D> 0, 2 корня
ах² + bх + c = а (х- х1 )(х - х2 ), где х1 и
х2 корни квадратного трехчлена
33.
Разложение на множители– х22 + 17х – 30
– х + 17х – 30 = 0
D=b2 – 4аc=(17)2– 4· (– 1)· (– 30) =
= 289 – 120 = 169
D> 0, 2 корня
ах² + bх + c = а (х- х1 )(х - х2 ),
где х1 и х2 корни квадратного трехчлена
х1=2
х2=15
Квадратный трёхчлен
– х2 + 17х - 30 = – (х –2)(х –15)
34.
Разложение на множители– х2 + 17х – 30
– х2 + 17х – 30 = 0
D=b2 – 4аc=(17)2– 4· (– 1)· (– 30) =
= 289 – 120 = 169
D> 0, 2 корня
ах² + bх + c = а (х- х1 )(х - х2 ),
где х1 и х2 корни квадратного
трехчлена
35.
Разложение на множители6х2 – 5х – 1
6х2 – 5х – 1 = 0
D=b2 – 4аc=(– 5)2– 4·6· (– 1) = 25
+ 24= 49
D> 0, 2 корня
ах² + bх + c = а (х- х1 )(х - х2 ),
где х1 и х2 корни квадратного
трехчлена
36.
Разложение на множители6х2 – 5х – 1
6х2 – 5х – 1 = 0
D=b2 – 4аc=(– 5)2– 4·6· (– 1) = 25 + 24= 49
D> 0, 2 корня
где х1 и х2
ах² + bх + c = а (х- х1 )(х - х2 ),
корни квадратного трехчлена
х1=1
х2= –
Квадратный трёхчлен
6х2 – 5х – 1 = 6 (х –1) (х –(– )) = ( х – 1) ( 6х + 2)
37.
Квадратным трёхчленом называетсямногочлен вида
ах² + bх + c,
где х - переменная, а, b и с некоторые числа,
причём а ≠0
ах² + bх + c = а (х - х1 )(х - х2 ), где
х1 и х2 корни квадратного
трехчлена
38.
Домашнее задание1.Найдите
корни квадратного трёхчлена:


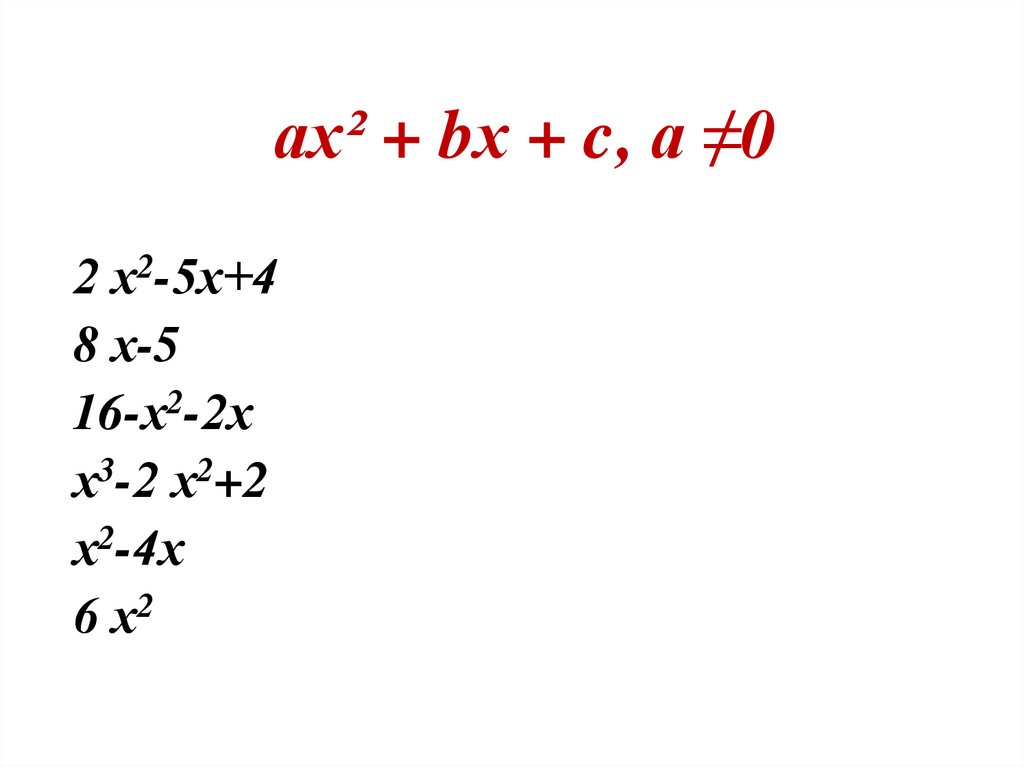
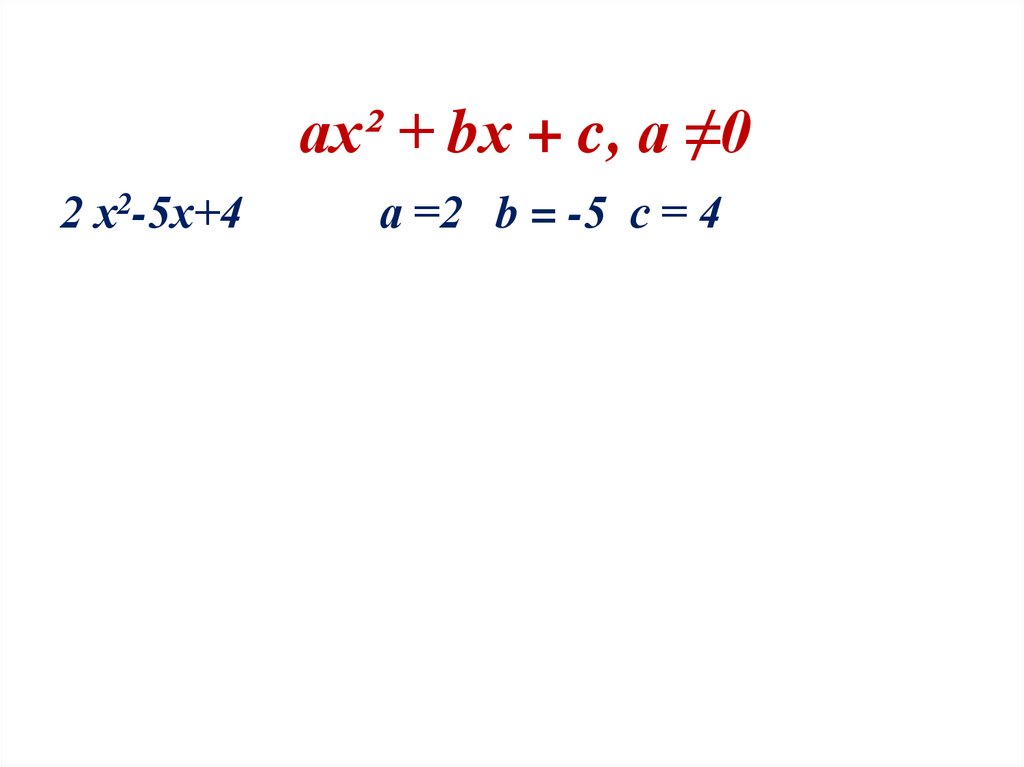













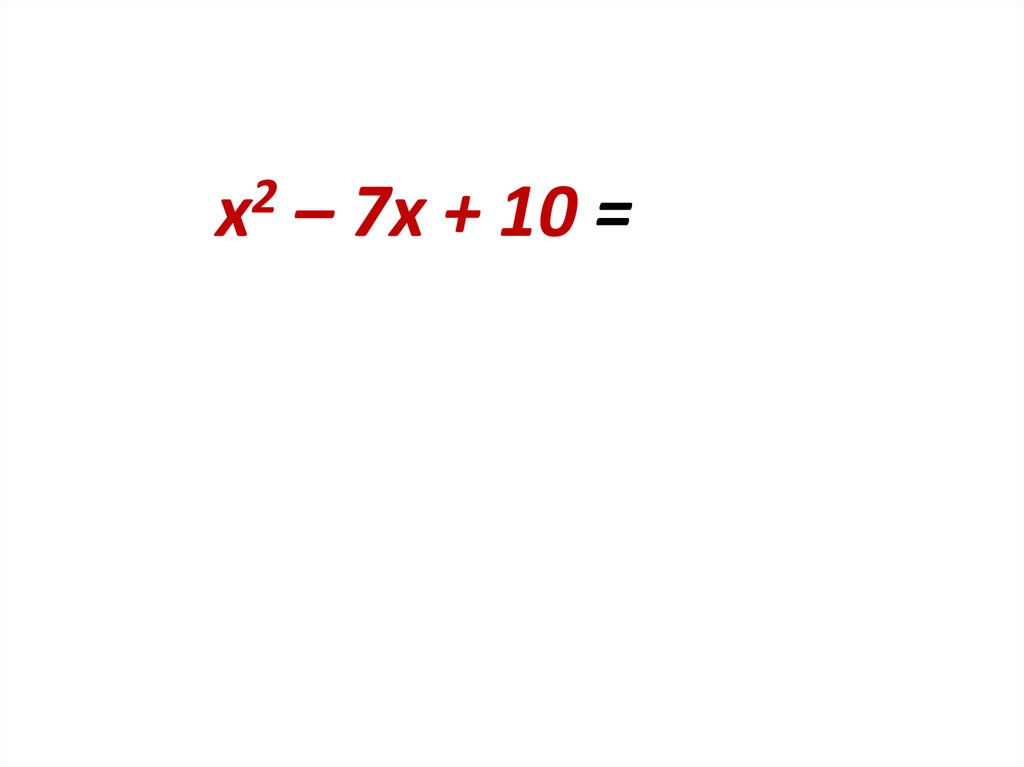
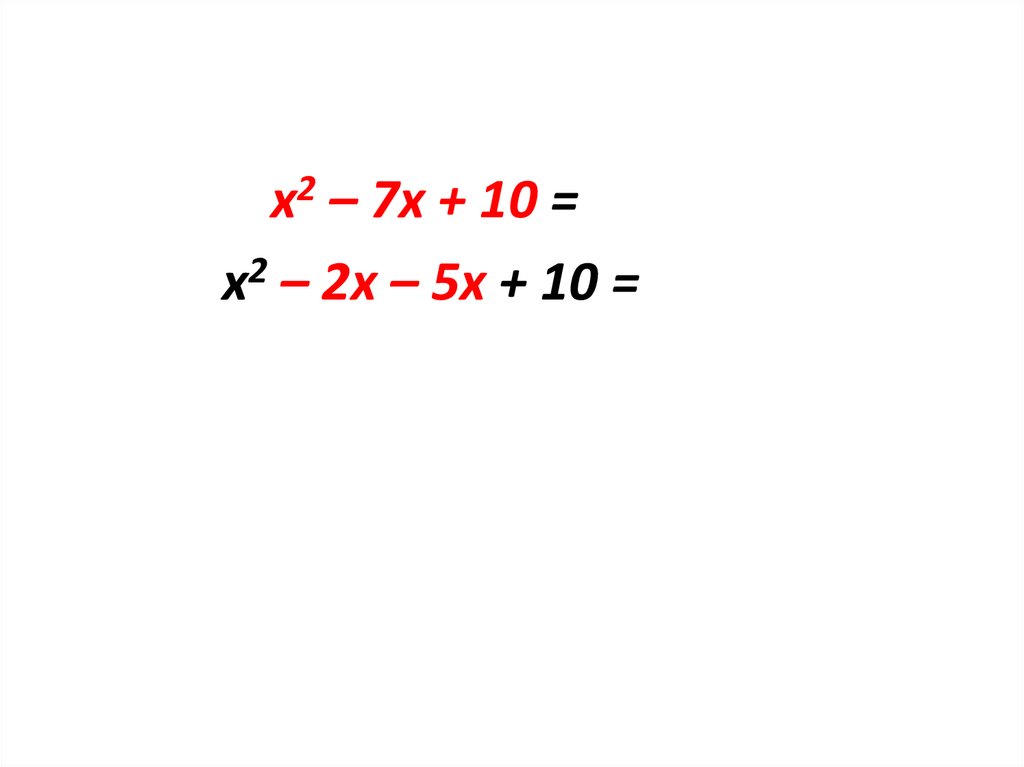



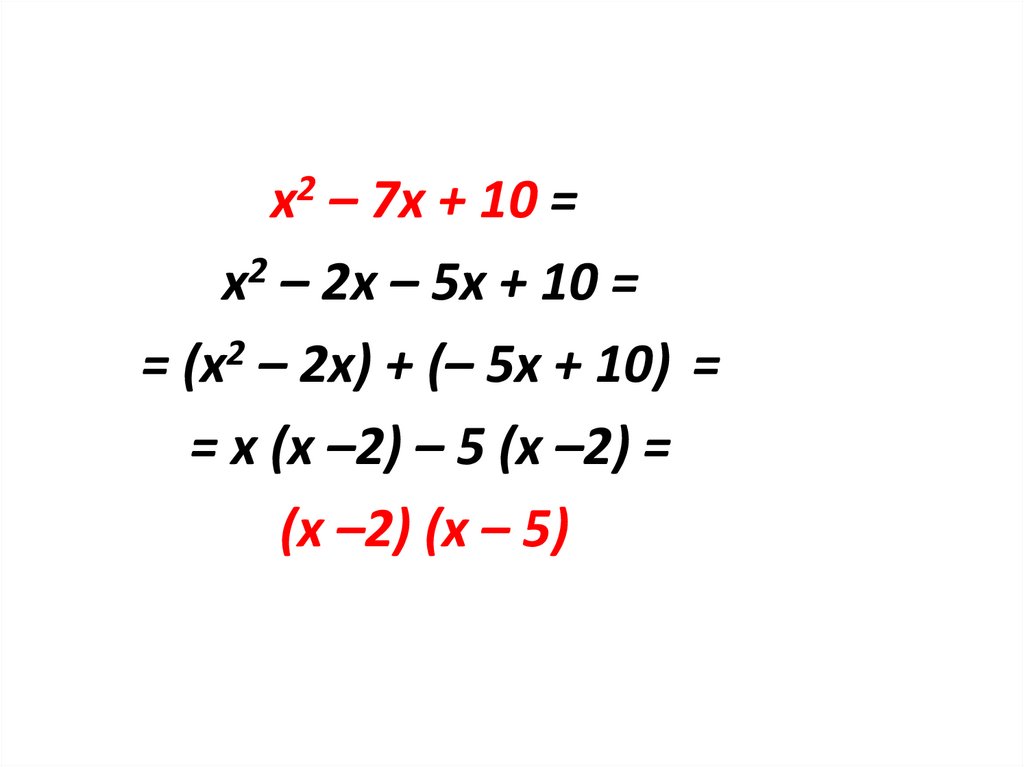















 Математика
Математика