Число степеней свободы

1.

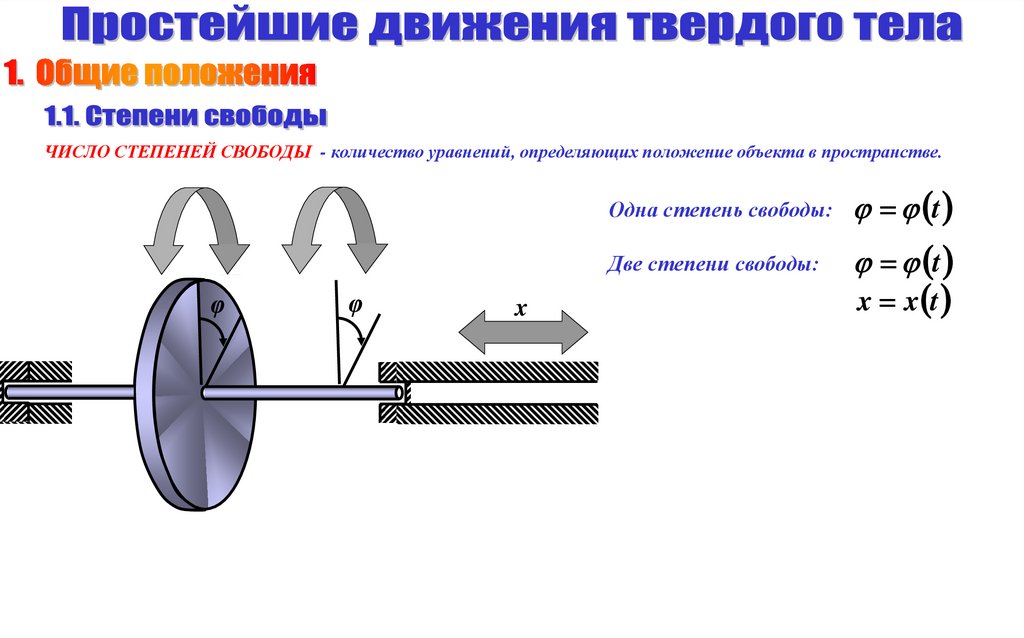
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ - количество уравнений, определяющих положение объекта в пространстве.
φ
φ
x
Одна степень свободы:
t
Две степени свободы:
t
x x t

2.

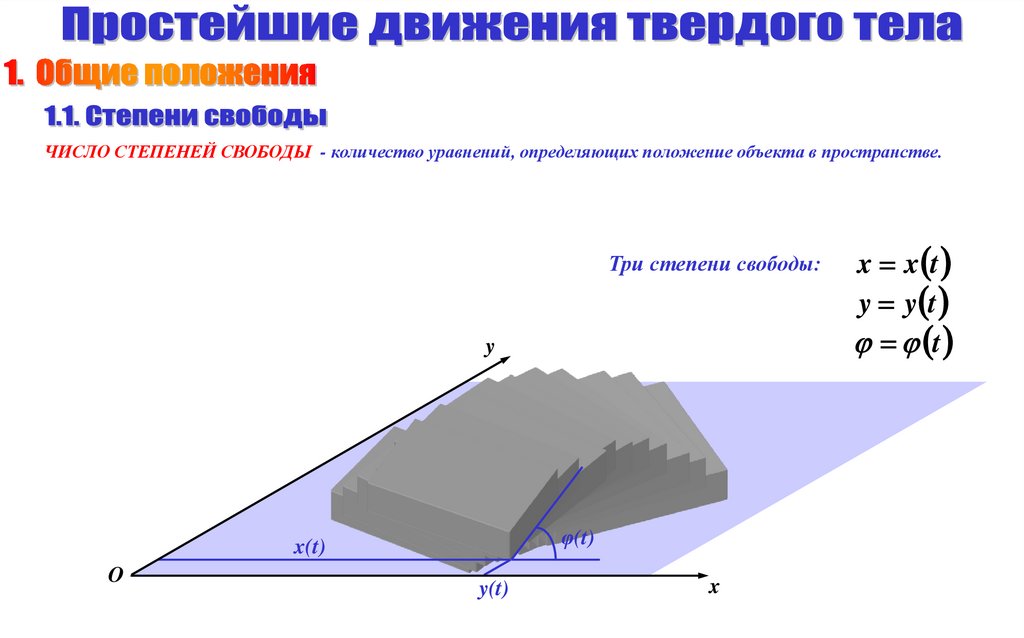
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ - количество уравнений, определяющих положение объекта в пространстве.
Три степени свободы:
y
φ(t)
x(t)
O
y(t)
x
x x t
y y t
t

3.

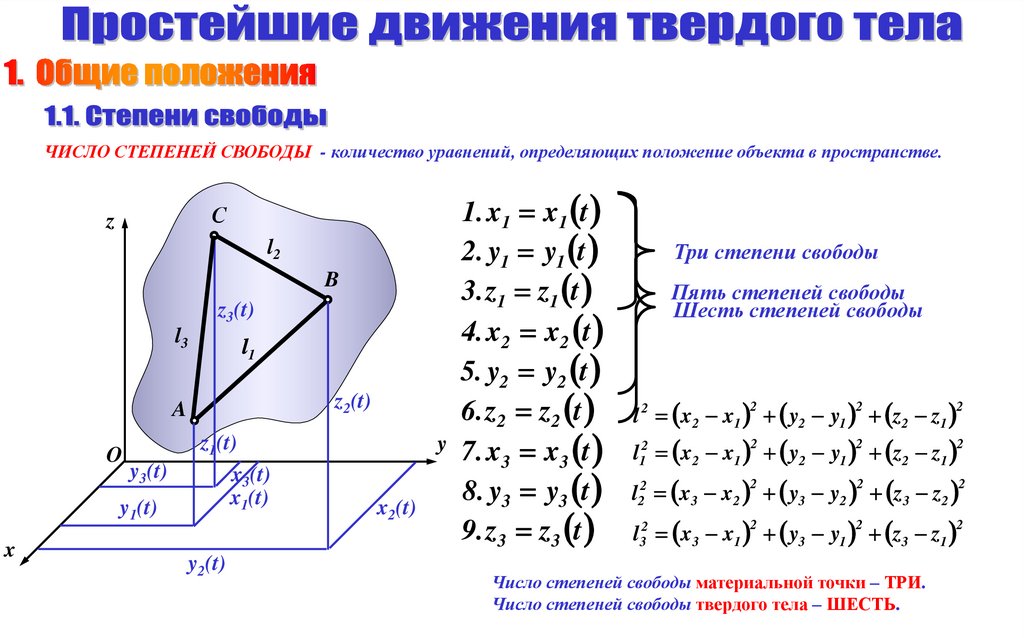
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ - количество уравнений, определяющих положение объекта в пространстве.
С
z
l2
B
z3(t)
l3
l1
z2(t)
A
O
y3(t)
y1(t)
x
z1(t)
x3(t)
x1(t)
y2(t)
x2(t)
1. x1 x1 t
2. y1 y1 t
3. z1 z1 t
4. x2 x2 t
5. y2 y2 t
6. z2 z2 t
y 7. x x t
3
3
8. y3 y3 t
9. z3 z3 t
Три степени свободы
Пять степеней свободы
Шесть степеней свободы
l x2 x1 y2 y1 z2 z1
2
2
2
2
l12 x2 x1 y2 y1 z2 z1
2
2
2
l22 x3 x2 y3 y2 z3 z2
2
2
2
l32 x3 x1 y3 y1 z3 z1
2
2
Число степеней свободы материальной точки – ТРИ.
Число степеней свободы твердого тела – ШЕСТЬ.
2

4.

drB drA d AB
rB rA AB ;
;
dt
dt
dt
d AB
vB v A
.
dt
d AB
d
AB
n ; n AB
dt
dt
n
A
900 φ
vA
z
прАВ (vA)
AB
rA
B
rB
O
x
прАВ (vB)
y
vB
d AB
AB
dt
vB( AB ) v A( AB ) 0 ;
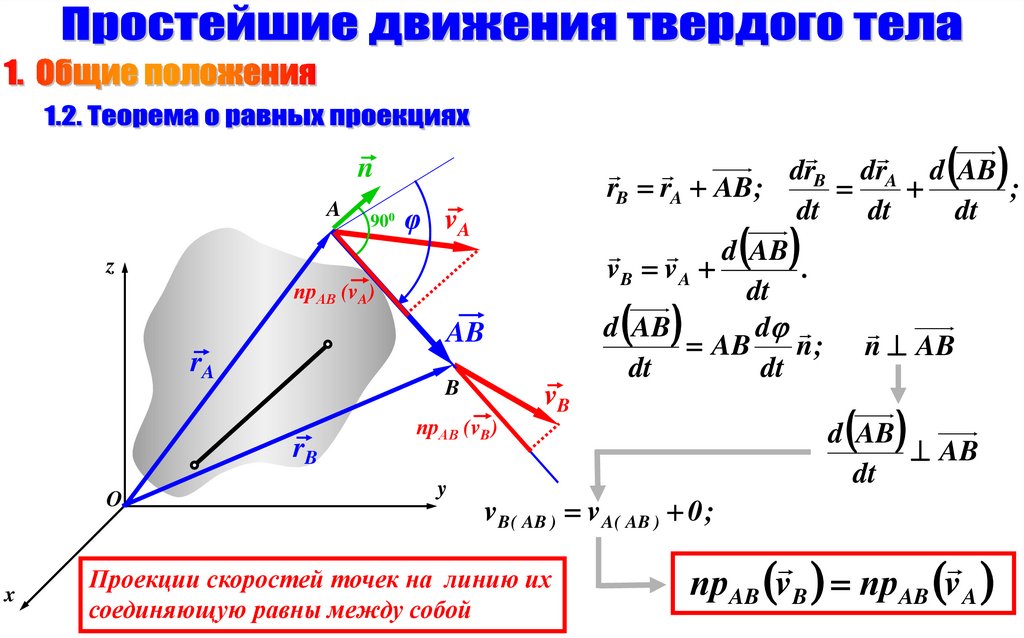
Проекции скоростей точек на линию их
соединяющую равны между собой
прAB vB прAB v A

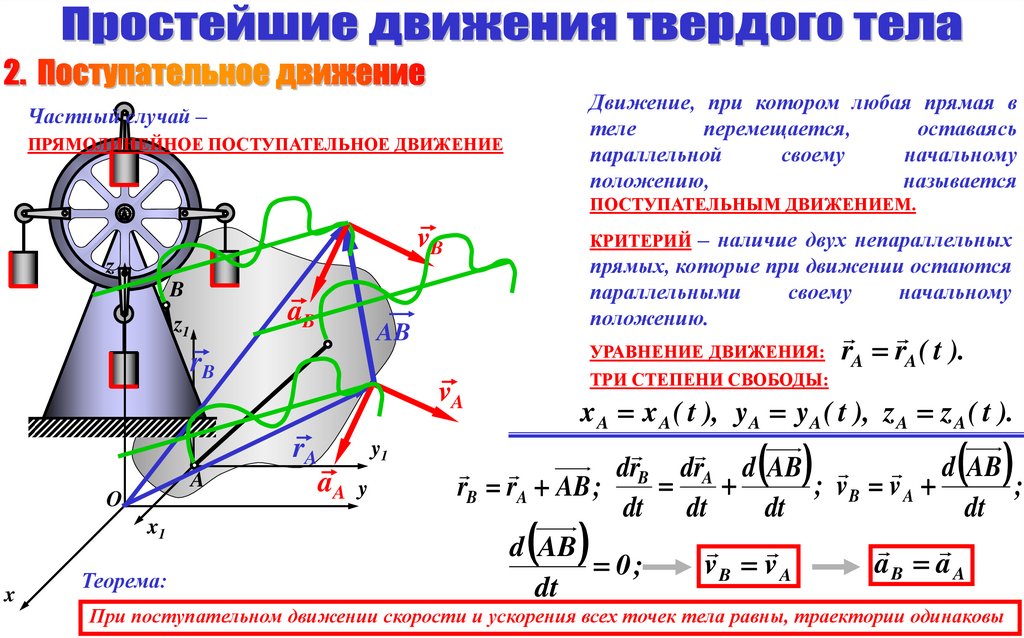
5.

Движение, при котором любая прямая в
теле
перемещается,
оставаясь
параллельной
своему
начальному
положению,
называется
Частный случай –
ПРЯМОЛИНЕЙНОЕ ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ
ПОСТУПАТЕЛЬНЫМ ДВИЖЕНИЕМ.
vB
z
B
aB
z1
x1
x
Теорема:
УРАВНЕНИЕ ДВИЖЕНИЯ: rA rA ( t ).
ТРИ СТЕПЕНИ СВОБОДЫ:
vA
rA
O
прямых, которые при движении остаются
параллельными
своему
начальному
положению.
AB
rB
A
КРИТЕРИЙ – наличие двух непараллельных
y1
aA y
x A x A ( t ), yA yA ( t ), z A z A ( t ).
drB drA d AB d AB
; vB v A
;
rB rA AB ;
dt
dt
dt
dt
d AB
aB a A
vB v A
0;
dt
При поступательном движении скорости и ускорения всех точек тела равны, траектории одинаковы

6.

ω
ε
О1
Движение тела, имеющего две неподвижные точки (О и О1 )
называется ВРАЩАТЕЛЬНЫМ ДВИЖЕНИЕМ.
Через две неподвижные точки может быть проведена прямая
(ОО1 ), называемая ОСЬ ВРАЩЕНИЯ.
УРАВНЕНИЕ ДВИЖЕНИЯ:
ε
ω
k
О
ОДНА СТЕПЕНЬ СВОБОДЫ
d d 2
2 .
dt
dt
k – единичный вектор, направленный по оси вращения k ; k .
ЕДИНИЦЫ ИЗМЕРЕНИЯ (CИ): φ – [ рад ], ω – [ рад /c]=[c -1], ε – [ рад /c2]=[c -2].
ТЕХНИЧЕСКИЕ ЕДИНИЦЫ ИЗМЕРЕНИЯ: N – [ об ], n – [ об /мин].
2 N , n .
30
РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЕ (ε=const):
0 t ; t 2
0 0 t
.
2
РАВНОМЕРНОЕ ВРАЩЕНИЕ (ε=0): t .
0
УГЛОВАЯ
СКОРОСТЬ:
φ
d
.
dt
( t ).
УГЛОВОЕ
УСКОРЕНИЕ:

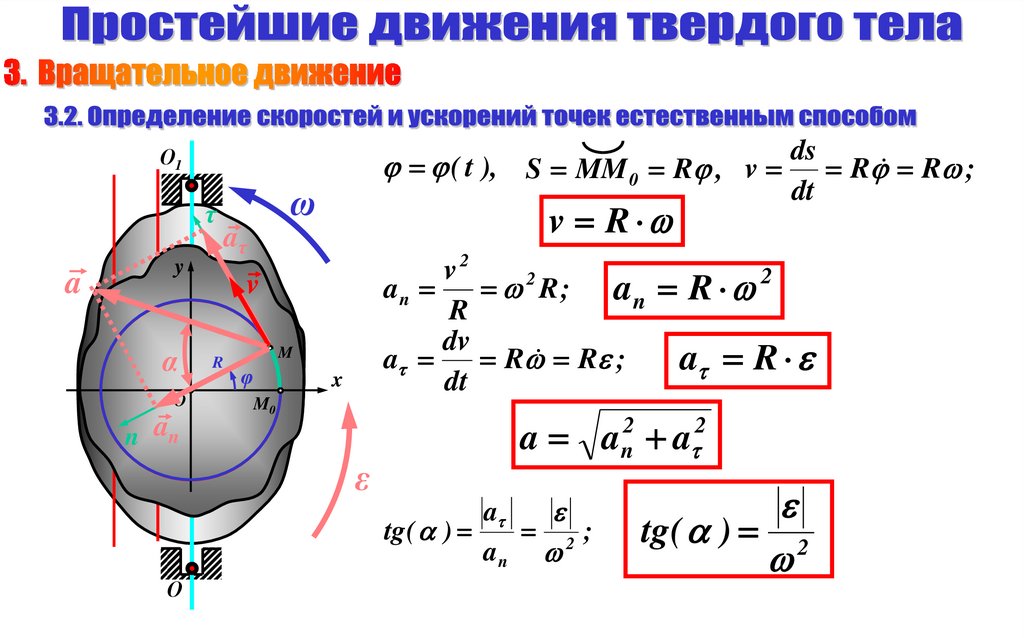
7.

ds
( t ), S MM 0 R , v R R ;
dt
О1
τ
a
y
α
O
n an
ω
v R
aτ
v2
2
2
an
R;
an R
R
dv
a
R R ;
a R
dt
v
R
M
φ
x
M0
ε
О
a a a
2
n
a
tg ( )
2;
an
2
tg ( ) 2

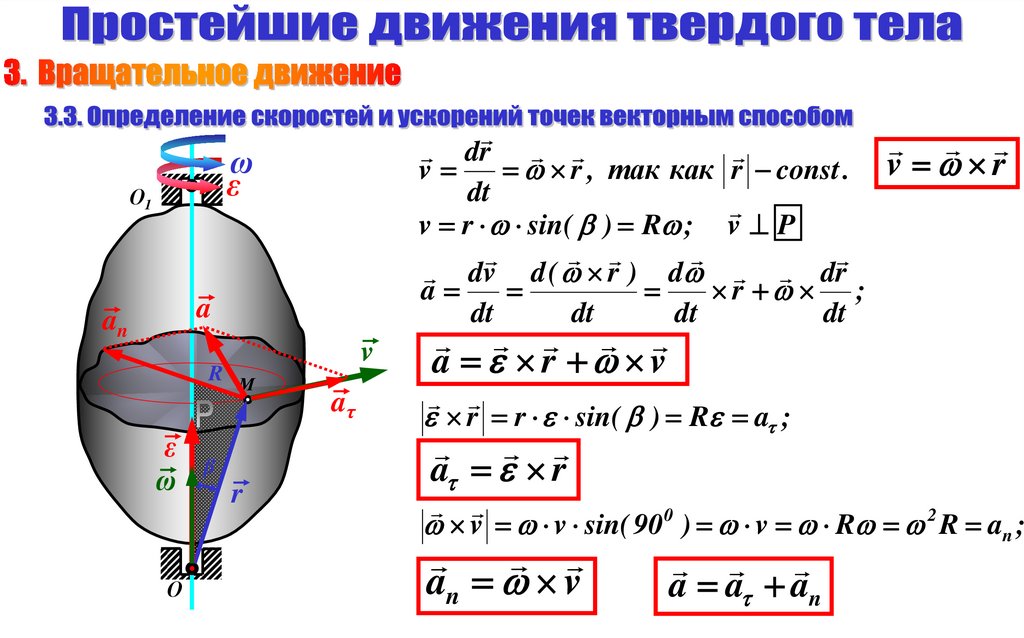
8.

dr
v
r , так как r const . v r
dt
v r sin( ) R ; v P
dv d ( r ) d dr
a
r ;
dt
dt
dt
dt
ω
ε
О1
a
an
R М
ε
ω
О
β
r
v
aτ
a r v
r r sin( ) R a ;
a r
v v sin( 90 0 ) v R 2 R an ;
an v
a a an

9.

3.4.1. Пример 1
A
O
vA
Колесо радиуса R = 0.5 м вращается равноускоренно из состояния
покоя. В момент времени t = 5 с скорость точек на ободе колеса
стала равна vA = 10 м/с. Определить сколько оборотов сделало
колесо за это время.
Решение:
v A 10
20 рад с ;
0 0 ;
R 0.5
0 20
2
0 t ;
4 рад с ;
t
5
2
2
t
25
t
4 50 рад ;
0 t ;
2
2
2
50
2 N ;
N
7.96 об ;
2 2 3.14
Ответ:
N 7.96 об ;

10.

3.4.2. Пример 2
Зубчатое колесо I, имеющее zI = 22 зуба, вращается по закону φ = 8t + 4t2 и
приводит в движение зубчатое колесо II, имеющее zII = 44 зуба. С колесом
II жестко скреплен барабан радиуса rБ = 6 см, на который наматывается
нить, поднимающая груз P. Определить скорость груза P и полное ускорение
точки M обода барабана в момент времени t = 1 c.
aτ
ωI
M
d
I 8 t 4 t 2 рад ; I I 8 8 t рад с ;
dt
r z
22 8 8 t
II I I I I
4 4 t рад с ; Б II 4 4 t рад с ;
aM
I
Решение:
an
ωII
rII
z II
44
vP Б rБ 4 4 t 6 см с ; При t = 1 c : vP 24 24 1 48 см с ;
II
Ускорение точки М :
εII
d II
4 рад с 2 ; a II rБ 4 6 24 см с 2 ;
dt
2
an Б2 rБ 4 4 t 6
64 6 384 см с 2 ;
II
t 1c
aM a 2 an2 24 2 384 2 384.75 см с 2 ;
P
Ответ: vP 48 см с ; aM 384.75 см с 2 ;

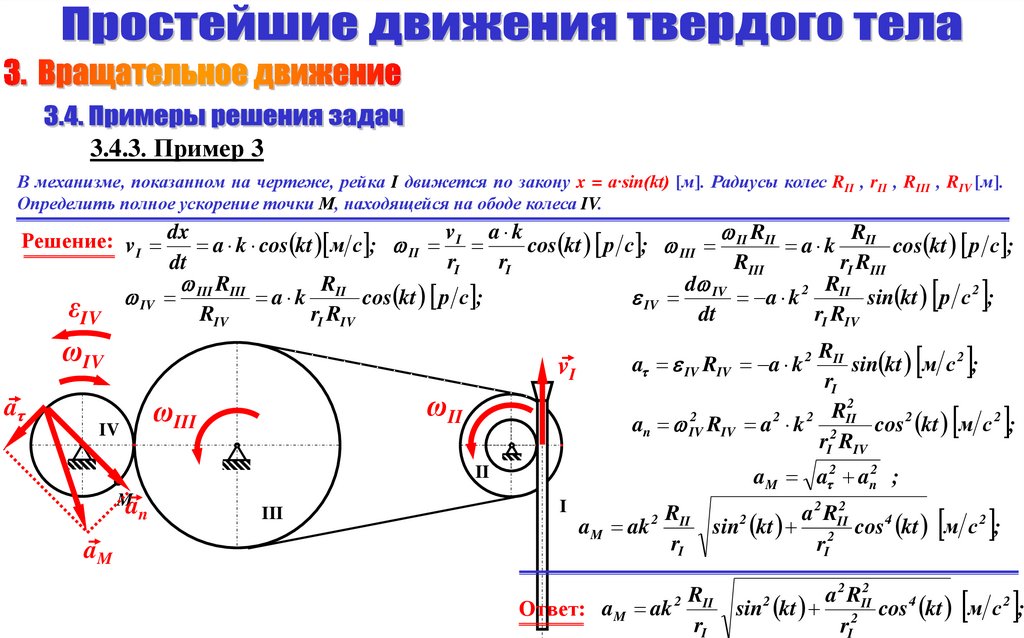
11.

3.4.3. Пример 3
В механизме, показанном на чертеже, рейка I движется по закону x = a·sin(kt) [м]. Радиусы колес RII , rII , RIII , RIV [м].
Определить полное ускорение точки М, находящейся на ободе колеса IV.
Решение: v I dx a k cos kt м с ; II v I a k cos kt р с ; III II RII a k RII cos kt р с ;
rI
rI
dt
RIII
rI RIII
III RIII
RII
d IV
2 RII
IV
a k
cos kt р с ;
IV
a k
sin kt р с 2 ;
εIV
RIV
rI RIV
dt
rI RIV
ωIV
aτ
vI
ωII
ωIII
IV
aM
n
III
RII
sin kt м с 2 ;
rI
2
2
2
2 RII
an IV RIV a k 2
cos 2 kt м с 2 ;
rI RIV
a IV RIV a k 2
aM a 2 an2 ;
II
Ma
I
R
aM ak 2 II
rI
2 2
a
R
sin2 kt 2 II cos 4 kt м с 2 ;
rI
2 RII
Ответ: aM ak
rI
2 2
a
RII
2
sin kt 2 cos 4 kt м с 2 ;
rI