Похожие презентации:
Введение в кинематику
1. КИНЕМАТИКА
8. ВВЕДЕНИЕ В КИНЕМАТИКУ8.1. Способы задания движения точки
Кинематикой называют раздел механики, в котором
рассматривают движение тел и точек без учета сил,
приложенных к ним.
Система отсчета - реальное или условное тело,
относительно которого определяют положение и
движение других тел.
Описание способов сводится к определению:
а) самой системы отсчета;
б) положения точки в пространстве;
в) уравнений движения точки;
г) формул, по которым могут быть найдены кинематические
характеристики движения точки.
2. 8.1.1. Векторный способ
Уравнение движения точкиr - радиус-вектор
r f t
Траекторией точки называют некоторую
линию, представляющую собой последовательность положений точки
относительно системы отсчета
Перемещением точки, r, за данный
промежуток времени называется вектор, i
соединяющий начальное и конечное
положения точки на ее траектории
r
a
k
O
r1
j
Vср
r0
M1
V
M0
Годографом радиуса-вектора называют линию, описываемую
его концом
3. Средняя скорость
r1 r0 rVср
t1 t0 t
Мгновенная скорость
dr
V lim Vср
t 0
dt
Ускорение точки - это векторная величина, характеризующая изменение скорости точки
dV
a
dt
4. 8.1.2. Естественный способ
Уравнение движения точкиS f t
b
ОМ = S – дуговая координата
Скорость точки
dS
V
dt
a a an
a
n an
(-)
Ускорение точки
Составляющие ускорения
dV d 2 S
a
2
dt
dt
V2
an
(+) τ
O
V
a
M
a - касательная со - ставляющая;
an нормальная составляющая.
5. 8.1.3. Координатный способ
УравненияxM f1 t
z
движения
y M f 2 t
a
точки
z M f 3 t
Vx 1 t
Скорость
точки V t
y
2
V
M
zM
x
2
2
2
Vz 3 t V Vx Vy Vz
yM
xM
Направляющие косинусы
cos Vx V , cos Vy V , cos Vz V .
Ускорение точки
a x dVx dt d 2 x dt 2 1 t
2
2
a y dV y dt d y dt 2 t
a ax2 a y2 az2
a z dVz dt d 2 z dt 2 3 t
y
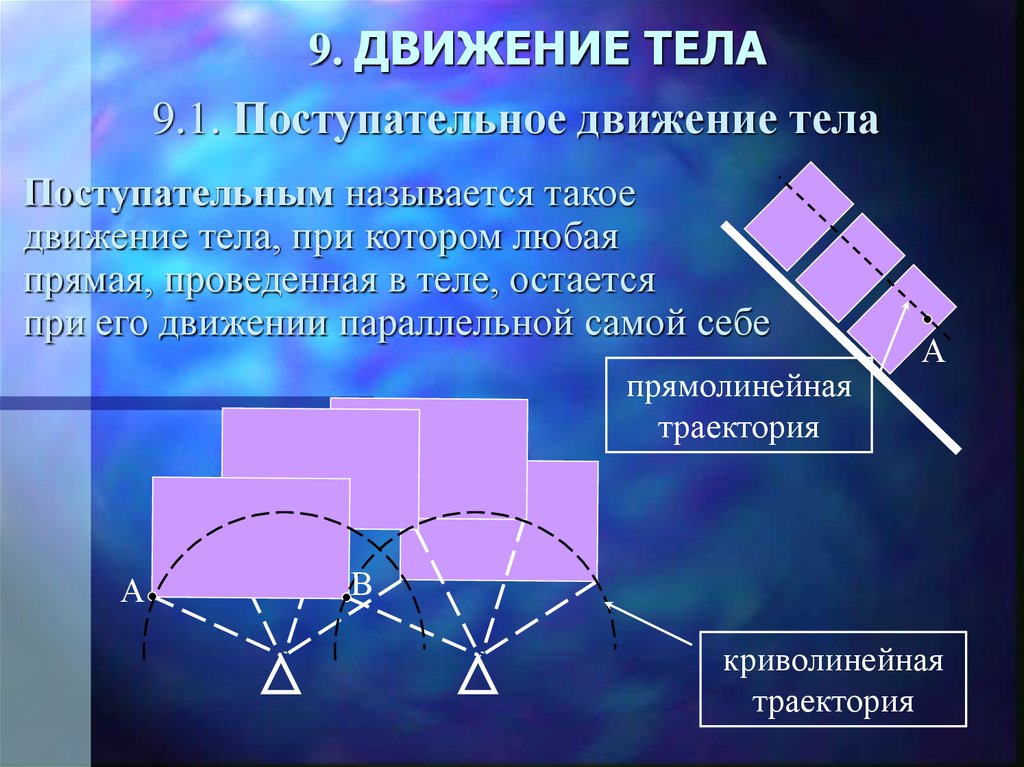
6. 9. ДВИЖЕНИЕ ТЕЛА
9.1. Поступательное движение телаПоступательным называется такое
движение тела, при котором любая
прямая, проведенная в теле, остается
при его движении параллельной самой себе
прямолинейная
траектория
А
А
В
криволинейная
траектория
7. Пример поступательного движения тела
8. Свойства поступательного движения
при поступательном движении все точки тела:- описывают одинаковые траектории;
- имеют в любой момент времени равные по модулю
и одинаковые по направлению скорости и ускорения
rB rA AB
В
rB
drB drA d AB
dt
dt
dt
d AB dt 0
2
d rB d rA
2
2
dt
dt
2
VB V A
aB a A
k
i
o
rA
B’
А
А’
j
rA f (t )
9. 9.2. Вращательное движение тела
Вращательным называется такое движение тела, прикотором хотя бы две его точки остаются неподвижными
B
Уравнение вращательного движения
f (t )
- угловая координата
φ
d
d
lim
lim
t 0 t
t 0 t
dt
dt
dS h d
V
h
dt
dt
dV d h
d
a
h
h
dt
dt
dt
V
dφ
c
M
I
dS
A
II
2
V 2 h
an
h 2
h
10. 9.3. Плоскопараллельное движение тела
Плоскопараллельным (плоским) называется такоедвижение тела, при котором все его точки описывают
траектории, параллельные некоторой неподвижной
плоскости
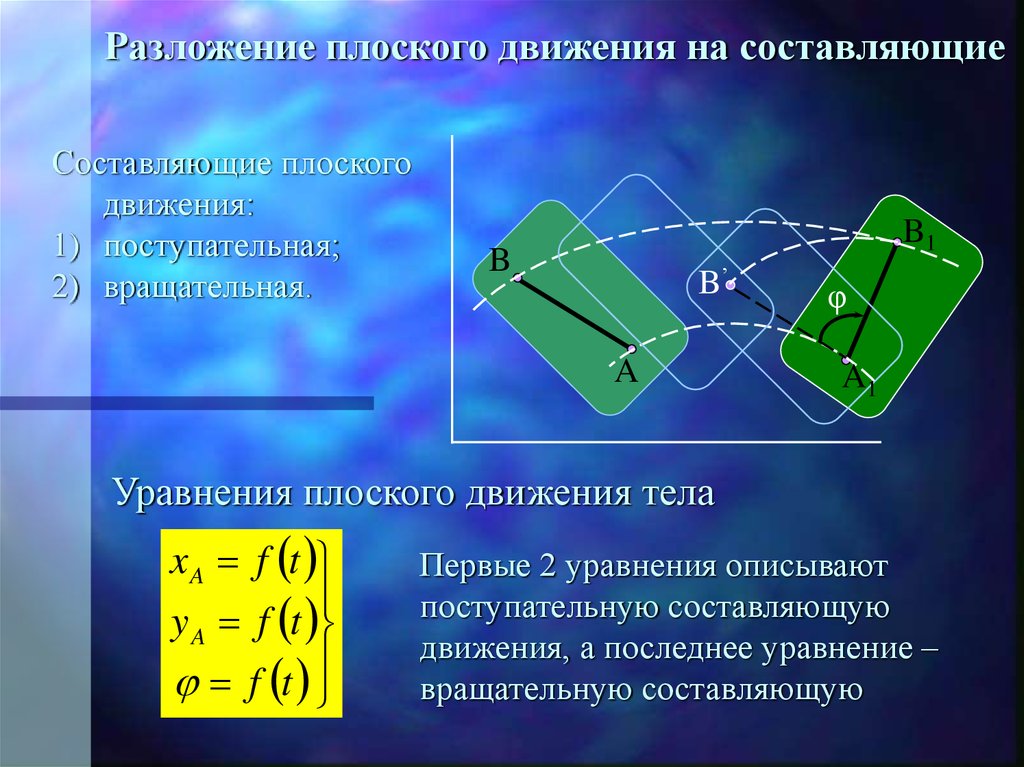
11. Разложение плоского движения на составляющие
Составляющие плоскогодвижения:
1) поступательная;
2) вращательная.
B1
B
B’
A
φ
A1
Уравнения плоского движения тела
x A f t
y A f t
f t
Первые 2 уравнения описывают
поступательную составляющую
движения, а последнее уравнение –
вращательную составляющую
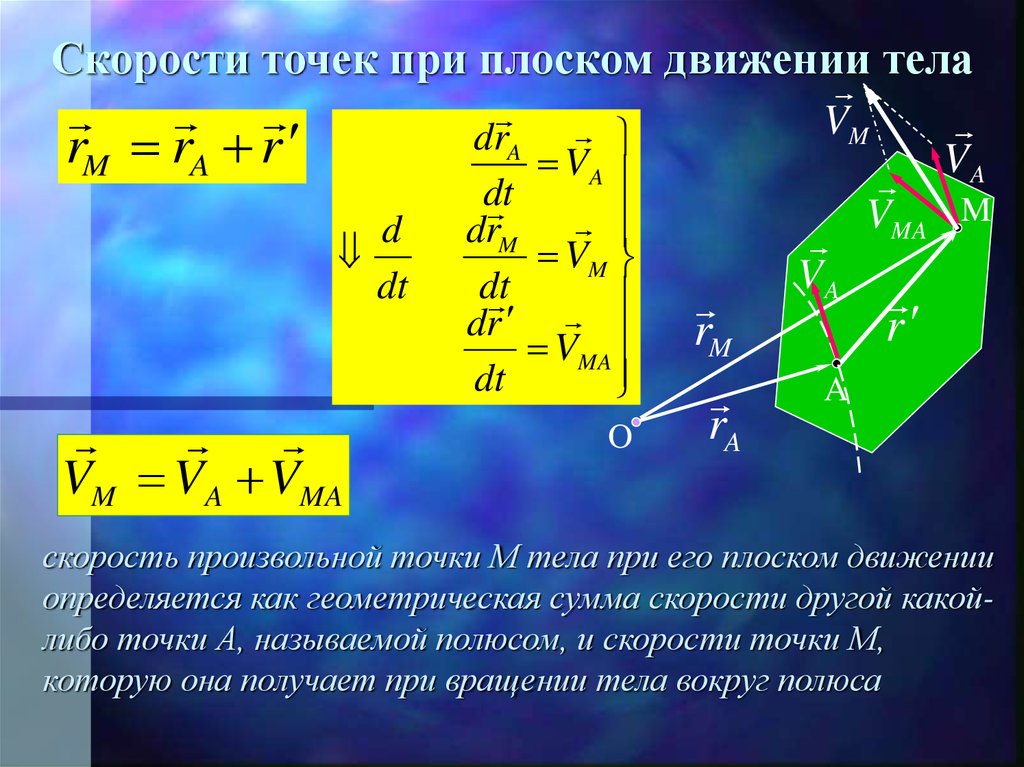
12. Скорости точек при плоском движении тела
rM rA rd
dt
VM VA VMA
drA
VA
dt
drM
VM
dt
dr
VMA
dt
O
VM
rM
rA
VA
VA
VMA M
r
A
скорость произвольной точки М тела при его плоском движении
определяется как геометрическая сумма скорости другой какойлибо точки А, называемой полюсом, и скорости точки М,
которую она получает при вращении тела вокруг полюса
13. Теорема о проекциях скоростей 2-х точек
проекции скоростей двух точек тела, совершающегоплоское движение, на прямую, проходящую через эти
точки, равны между собой
VB V A VBA
VB V
A
VBx VAx VBAx
VBx VB cos
VA
VBA
x
B
A
VAx VA cos
VB cos VA cos
VBAx VBA cos 90 0
14. Мгновенный центр скоростей (МЦС)
МЦС - точка сечения тела, скорость которой вданный момент времени равна нулю
VA
A
Пусть V p 0, тогда одно
временно должно выполняться
B
90o
90o
VB
V AAP VPAP и VBBP VPBP ,
что невозможно , поэтому
VP 0
P
Скорость произвольной точки М
тела равна VM VMP или VM MP
15. ВЫВОДЫ:
1) практическое значение МЦС заключается втом, что с его помощью геометрически
сложное плоское движение тела можно
рассматривать как простое мгновенно
вращательное движение относительно оси,
проходящей через МЦС;
2) скорость произвольной точки тела,
совершающего плоское движение,
определяется как скорость, которую она
получает при вращении тела вокруг МЦС
16. Частные случаи определения положения МЦС
a)A
ω
P
VA
A
B
90o
B
VB
VC ω
C
90o
P
VB
VA
A
B
b)
VA VB
AP BP
P
c)
VA
VB
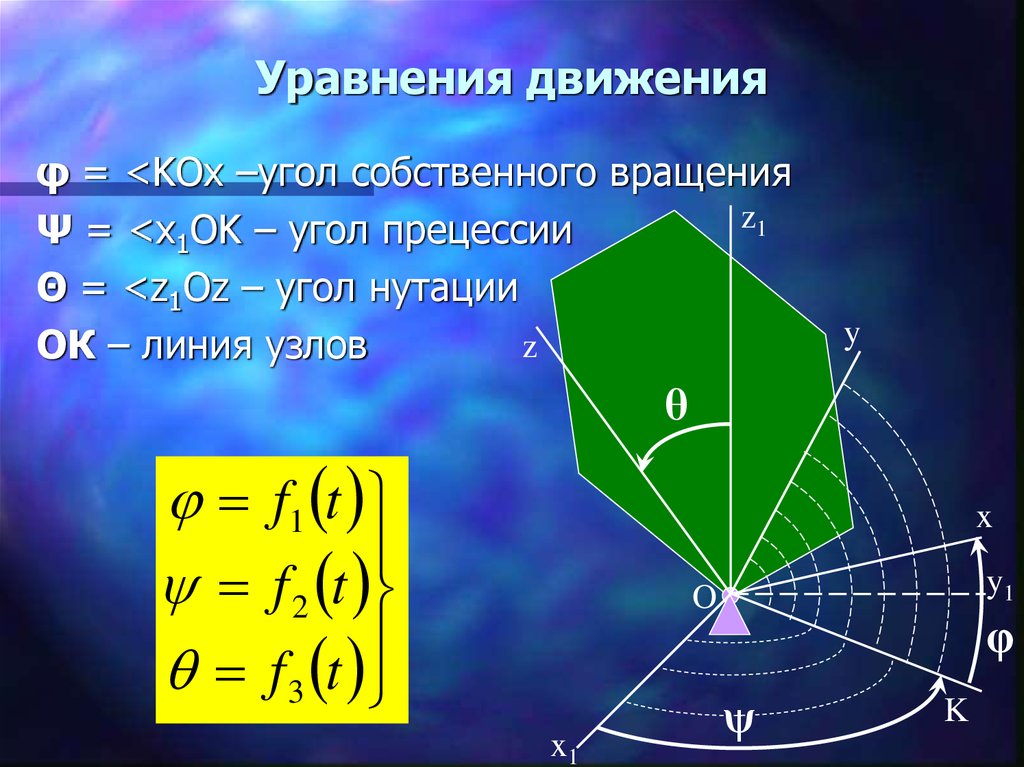
17. 9.4. Движение тела с одной неподвижной точкой
18. Уравнения движения
φ = <KOx –угол собственного вращенияz1
Ψ = <x1OK – угол прецессии
Θ = <z1Oz – угол нутации
z
ОК – линия узлов
y
θ
f1 t
f 2 t
f 3 t
x
y1
O
x1
φ
ψ
K
19. Теорема Эйлера-Даламбера
всякое элементарное перемещение тела, имеющегоодну неподвижную точку, можно представить как
элементарный поворот относительно мгновенной
оси вращения, проходящей через эту точку
Найдем М , где
h1 d h2 d ,
т.е.
h1 d h2 d 0
N
z
h1
z1
h2
dψ
М
P
dφ
dφ+dψ
dθ
О
К
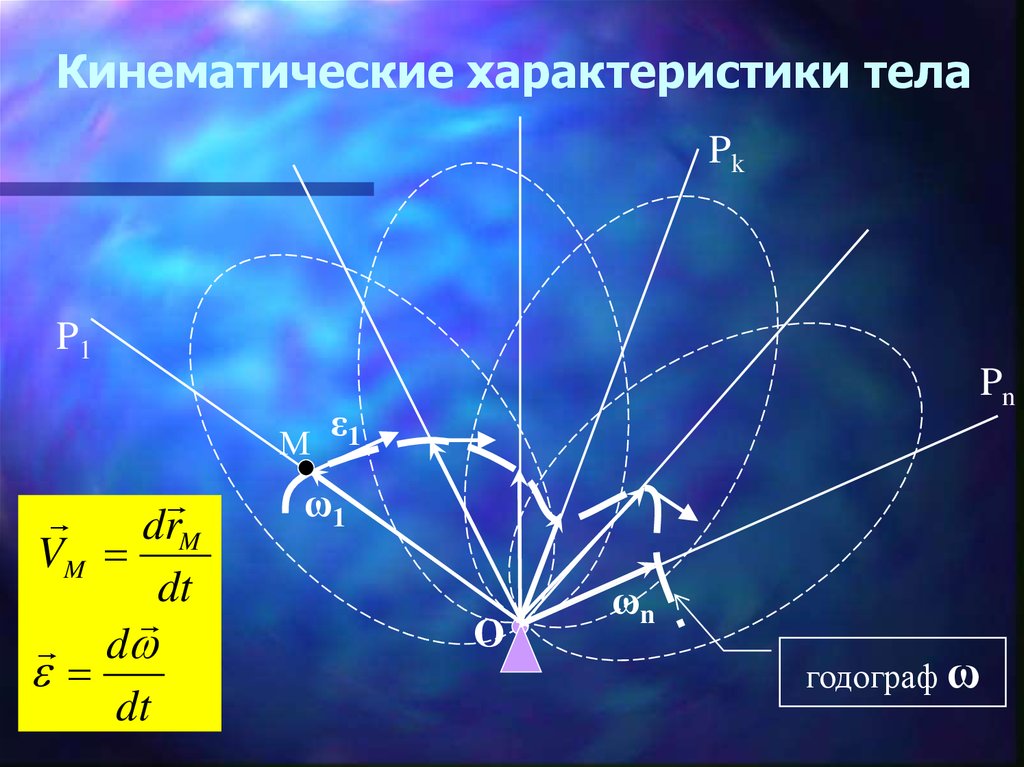
20. Кинематические характеристики тела
PkP1
М
drM
VM
dt
d
dt
Pn
ε1
ω1
O
ωn
годограф ω
21. Кинематические характеристики точки
PV r
r r sin h
dV
a
dt
dr
d
r
dt
dt
r V
a r
h
α
O
М
V
rM
a n V
22. 9.5. Движение свободного тела
z1Уравнения движения тела :
x1 A f1 t y1 A f 2 t z1 A f 3 t
f 4 t f 5 t f 6 t
Скорость точки М :
VM VA VMA
VMA AM
Ускорение точки М :
aM a A aMA
P
VA
x
VA
z
M VMA
y
A
O
x1
VM
y1
a MA AM VMA
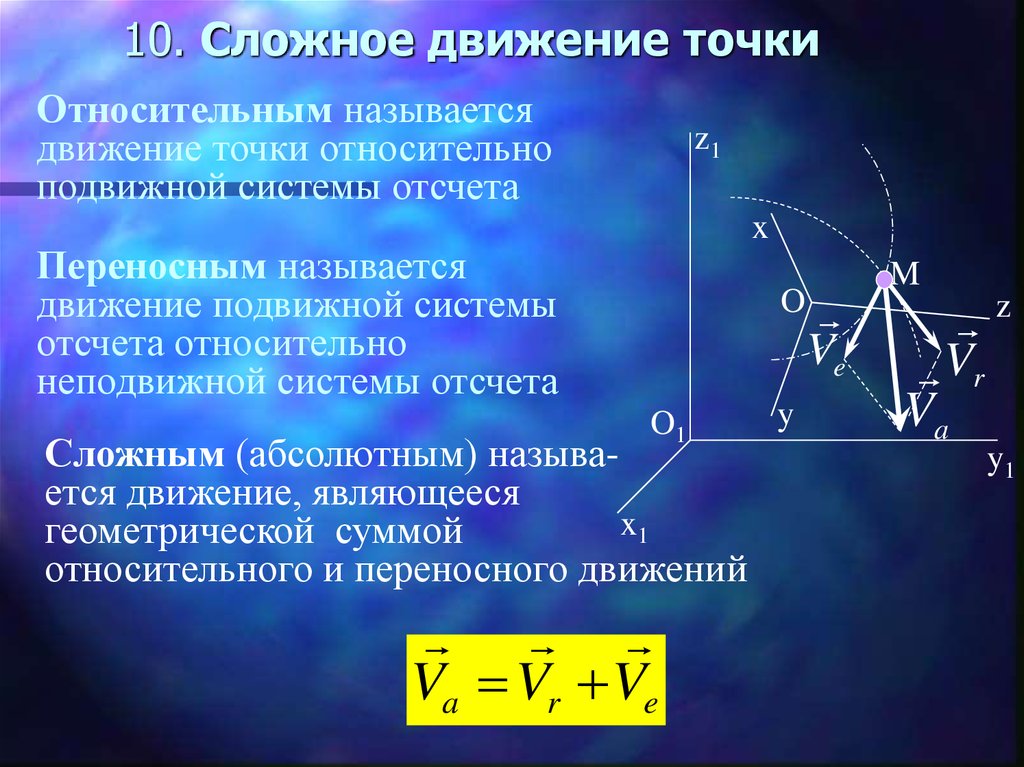
23. 10. Сложное движение точки
Относительным называетсядвижение точки относительно
подвижной системы отсчета
z1
x
Переносным называется
движение подвижной системы
отсчета относительно
неподвижной системы отсчета
O
O1
Сложным (абсолютным) называется движение, являющееся
x1
геометрической суммой
относительного и переносного движений
Va Vr Ve
y
Ve
M
z
Vr
Va
y1
24. 10.2. Ускорение точки
a a a r ae acУскорение Кориолиса учитывает влияние относительного движения точки на переносную скорость и
переносного движения на относительную скорость
ac 2 e Vr ac 2 eVr sin e , Vr
Правило Н.Е.Жуковского: спроектировать вектор относительной скорости, Vr ,
на плоскость, перпендикулярную оси
вращения, и полученную проекцию, Vrxy ,
довернуть в этой же плоскости на 90 по
направлению вращения
z
ω
x
Vr
y
V
ac M rxy
25. Случаи ac=0:
1) ωe=0 – подвижная система отсчетадвижется поступательно;
B
2) Vr=0 – в относительном движении
скорость точки может быть
A
равна нулю, как частное
e
значение;
O
3) sin e ˆ, Vr 0 - вектор
угловой скорости параллелен
вектору относительной скорости.
l0
V r A ,B 0
Vr


















 Физика
Физика








