Похожие презентации:
Элементарные булевы функции и их свойства
1.
Элементарныебулевы функции и их
свойства
2.
Элементарные булевыфункции
Среди булевых функций особо выделяются так
называемые элементарные булевы функции, посредством которых
можно описать любую булеву функцию от любого числа
переменных.
3.
ОпределенияОпределение. Булевой (логической) переменной называется переменная,
принимающая лишь два значения « 0 » и «1».
Определение. Булевой функцией от n логических
переменных называется функция, прини мающая также лишь два
значения « 0 » и «1».
Определение. Если функция не зависит от некоторой переменной, то
такую переменную будем называть фиктивной (несущественной)
4.
Тождественная единицаБулева функция f(x1, x2 … xn) принимающая значение 1 на всех наборах
нулей и единиц называется константой 1, или тождественной единицей.
Обозначение: 1.
5.
Тождественный нульБулева функция f(x1, x2 … xn) принимающая значение 0 на всех
наборах нулей и единиц называется константой 0, или
тождественным нулем. Обозначение: 0.
6.
ОтрицаниеОтрицанием называется булева функция одной переменной, которая
определяется следующей таблицей истинности:
Обозначения: ¬x. Запись ¬x читается «не икс» или «отрицание икс».
7.
КонъюнкцияКонъюнкцией называется булева функция двух переменных, которая
определяется следующей таблицей истинности:
Определение. Конъюнкцией n переменных f =
x1 x2 ...xn называется функция, которая принимает значение 1,
тогда и только тогда, когда все переменные равны 1 (и, значит,
равна 0, если хотя бы одна из этих переменных равна 0).
8.
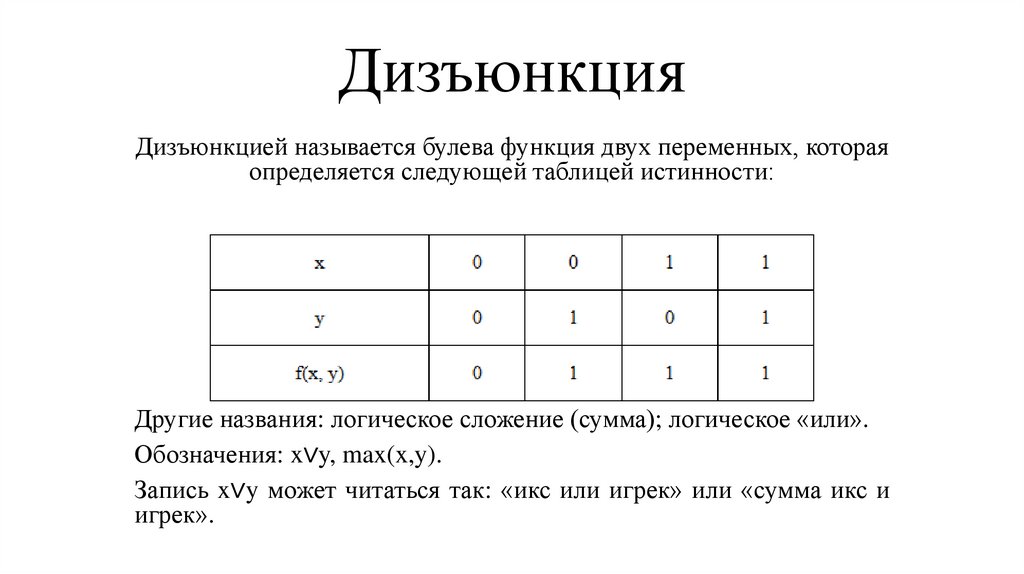
ДизъюнкцияДизъюнкцией называется булева функция двух переменных, которая
определяется следующей таблицей истинности:
Другие названия: логическое сложение (сумма); логическое «или».
Обозначения: x∨y, max(x,y).
Запись x∨y может читаться так: «икс или игрек» или «сумма икс и
игрек».
9.
Определение дизъюнкцииОпределение. Дизъюнкцией n переменных f = x1v x2v ... v
xn называется такая функция, которая равна 0 тогда и только
тогда, когда все переменные равны 0 (и, значит, равна 1, когда
хотя бы одна из этих переменных равна 1).
10.
ИмпликациейИмпликацией называется булева функция двух переменных, которая
определяется следующей таблицей истинности:
Другое название: логическое следование.
Обозначения: x→y, x⇒y, x⊃y.
Запись x→y может читаться так: «из икс следует игрек».
11.
ЭквивалентностьЭквивалентностью называется булева функция двух переменных,
которая определяется следующей таблицей истинности:
Обозначения: x∼y, x↔y.
Запись x∼y может читаться так: «икс эквивалентно игрек» или «икс
равносильно игрек».
12.
Cумма по модулюCуммой по модулю 2 называется булева функция двух переменных,
которая определяется следующей таблицей истинности:
Другое название: антиэквивалентность.
Обозначения: x⊕y, x+y.
Запись x⊕y может читаться так: «икс плюс игрек».
13.
Штрих ШеффераШтрих Шеффера это булева функция двух переменных, которая
определяется следующей таблицей истинности:
Другое название: отрицание конъюнкции, логическое «не-и».
Обозначение: x|y.
Запись x|y может читаться так: «не икс или не игрек», «икс и игрек
несовместны», «икс штрих Шеффера игрек».
14.
Стрелка ПирсаСтрелка Пирса это булева функция двух переменных, которая
определяется следующей таблицей истинности:
Другое название: отрицание дизъюнкции, логическое «не-или»,
функция Вебба.
Обозначение: x↓y; для функции Вебба — x°y.
Запись x↓y может читаться так: «ни икс и ни игрек», «икс стрелка
Пирса игрек».
15.
16.
Основные свойства этихфункций:
1) Закон двойного отрицания
2) Ассоциативность конъюнкции и дизъюнкции
x ∨ (y ∨ z) = (x ∨ y) ∨ z = x ∨ y ∨ z, x ∧ (y ∧ z) = (x ∧ y) ∧ z.
3) Коммутативность x ∧ y = y ∧ x, x ∨ y = y ∨ x.
4) Дистрибутивность x (y ∨ z) = xy ∨ xz; x ∨ (yz) = (x ∨ y) (x ∨ z).
5) Идемпотентность x ∧ x = x, x ∨ x = x.
6) Свойства констант 0 и 1 x ∧ 1 = x, x ∨ 1 = 1, x ∧ 0 = 0, x ∨ 0 = x, 0 = 1, 1 = 0.
7)Правила де Моргана x ∧ y = x ∨ y; x ∨ y = x ∧ y.
8) Закон противоречия x ∧ x = 0 .
9)Закон исключённого третьего x ∨ x = 1.
Наряду с основными соотношениями для упрощения формул часто используют следующие
эквивалентные соотношения, выводимые из основных с помощью эквивалентных
преобразований, а именно:
1) Поглощение («Целое поглощает часть») x ∨ xy = x; x (x ∨ y) = x.
2) Склеивание xy ∨ xy = x.
3) Обобщённое склеивание xz ∨ yz ∨ xy = xz ∨ yz.
17.
Спасибоза
внимание
















 Математика
Математика








