Похожие презентации:
Переміщення та перетворення подібності
1.
2.
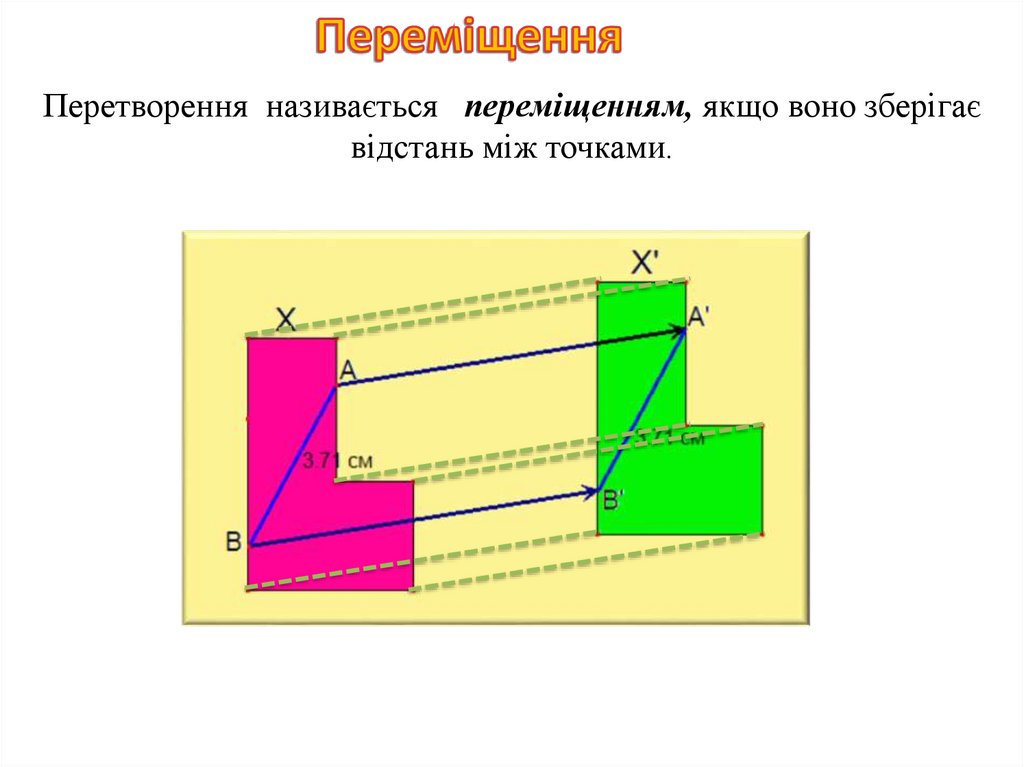
Перетворення називається переміщенням, якщо воно зберігаєвідстань між точками.
3.
При переміщенні точки, що лежать на прямій,переходять у точки, що лежать на прямій, і
зберігається порядок їх взаємного розміщення.
A
B
A’
B’
AB =A’B’
4.
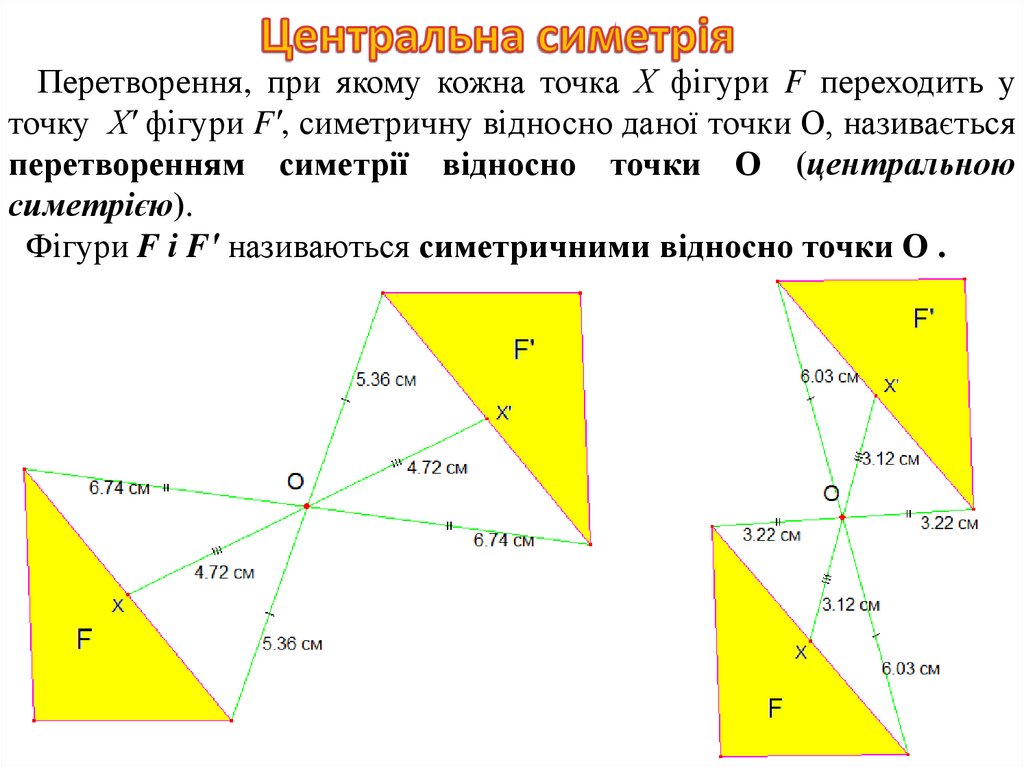
Перетворення, при якому кожна точка Х фігури F переходить уточку Х′ фігури F′, симетричну відносно даної точки О, називається
перетворенням симетрії відносно точки О (центральною
симетрією).
Фігури F і F′ називаються симетричними відносно точки О .
5.
Перетворення, при якому кожна точка А фігури Fпереходить у точку А′ фігури F′, симетричну відносно даної
прямої l, називається перетворенням симетрії відносно
прямої l.
При цьому фігури F і F′
називаються симетричними
відносно прямої l.
Пряма l - вісь симетрії.
6.
відносно площини ХОУ рис. 1:відносно площини УОZ рис. 3:
відносно площини ХОZ рис. 2:
7.
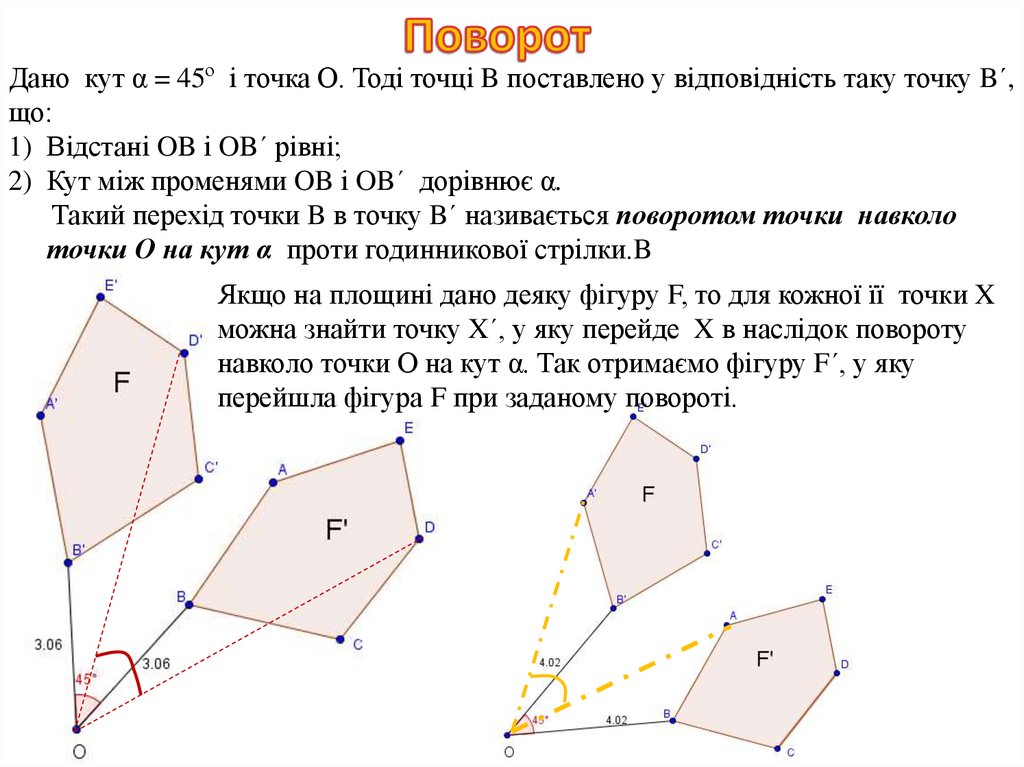
Дано кут α = 45º і точка О. Тоді точці B поставлено у відповідність таку точку B´,що:
1) Відстані OB і OB´ рівні;
2) Кут між променями OB і OB´ дорівнює α.
Такий перехід точки B в точку B´ називається поворотом точки навколо
точки О на кут α проти годинникової стрілки.B
Якщо на площині дано деяку фігуру F, то для кожної її точки X
можна знайти точку X´, у яку перейде X в наслідок повороту
навколо точки О на кут α. Так отримаємо фігуру F´, у яку
перейшла фігура F при заданому повороті.
8.
Поворот фігур F відносно точки Hна кут 90.˚
9.
Перетворення при якому всі точки фігури зміщуються в одномуй тому самому напрямі і на одну й ту саму відстань, називається
паралельним перенесенням.
10.
Перетворення називається гомотетичним, якщо воно переводитькожну точку X фігури F у точку X’ фігури F’ так, що ОX=|k| OX,
де k – будь-яке число, відмінне від 0, О – фіксована точка.
k – коефіцієнт гомотетії,
O - центр гомотетії.
11.
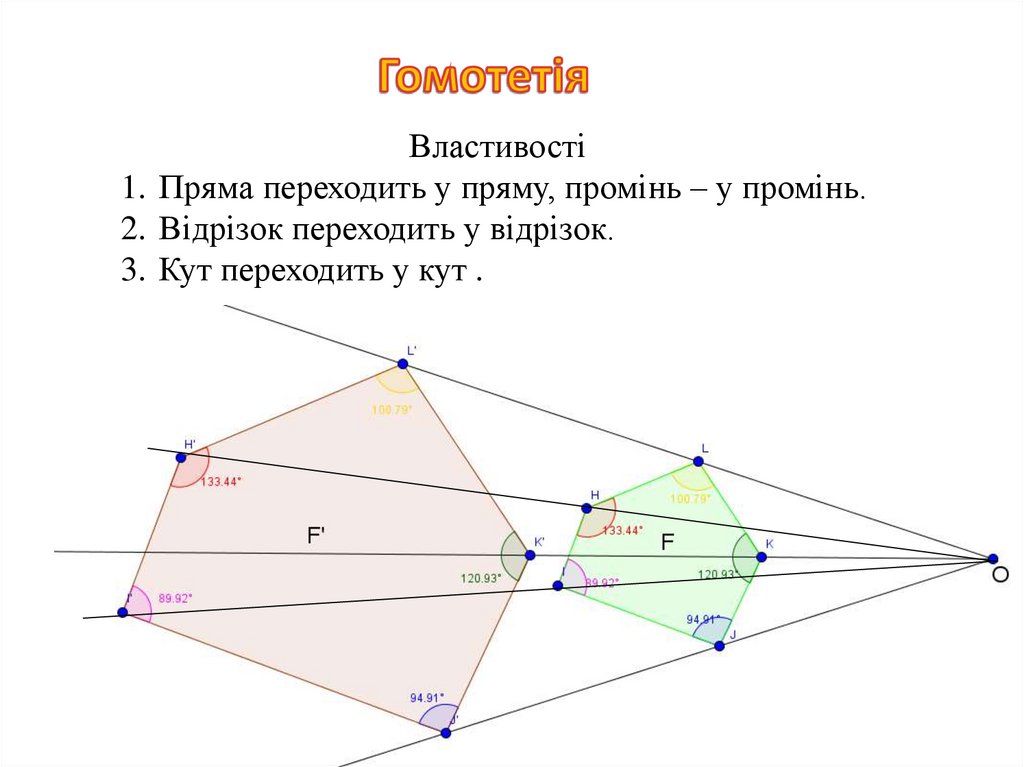
Властивості1. Пряма переходить у пряму, промінь – у промінь.
2. Відрізок переходить у відрізок.
3. Кут переходить у кут .
12.
1. Задача №1.Дано точки А(5;4;-9), В(0;-1;2);
С(2;-7;-3). Знайдіть точки, симетричні даним відносно
координатних площин.
2. Задача №2.
Знайдіть координати точки, гомотетичної точці А(4;6;9)
відносно початку координат, якщо коефіцієнт гомотетії а)
k =– 3; б) k= 0.5
3. Задача №3.
Записати координати точки А’, в яку переходить точка
А(-4;12;-13) при виконанні двох послідовних симетрій
відносно площин ХОУ та УOZ.
13.
А(5;4;-3),Z
B(4, 6, 9)
B
B’
A’
O
A”
A’’’
A
X
OB”=-3*OB
B”
Y









 Математика
Математика