Перетворення подібності. Гомотерапія

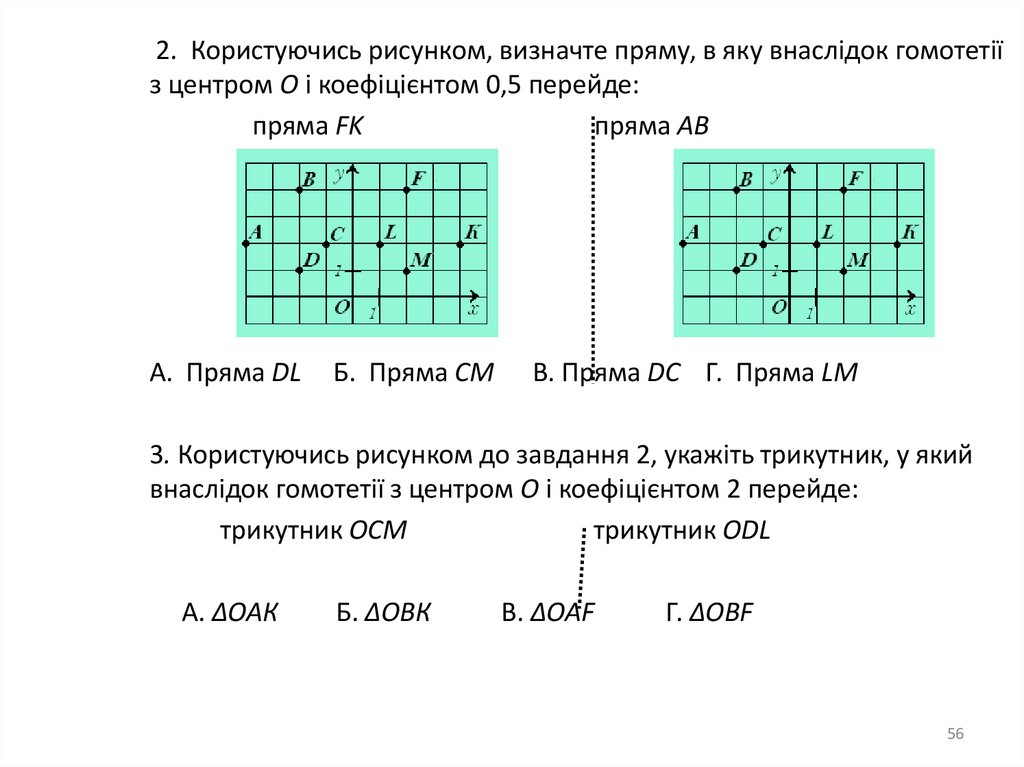
1.

Уявіть собі, що ви біля ставка, кидаєте камінці
у воду і спостерігаєте як на поверхні
утворюються хвилі у вигляді концентричних
кіл (центр кожного кола розміщений саме там,
де камінець торкнувся води)
Станьте перед дзеркалом, підніміть праву
руку - і дзеркало «перетворить» вас на лівшу
(ваш двійник підняв ліву руку).
У шухляді вашого столу лежить косинець;
ви трохи висунули шухляду –
і косинець перемістився
разом з нею.
Так чи інакше, в кожному з
цих випадків фігури, про які
йдеться, зазнають певних змін, перетворень.

2.

Спроби правильно відобразити на плоскому
рисунку природні форми предметів були задовго до
виникнення писемності – люди малювали на стінах
печер рослини, тварин тощо. Тривала практика
підказувала митцям, як передати на рисунку
зображуваний предмет - так зароджувалося вчення про
відповідності й перетворення.
За допомогою геометричних перетворень і
комп’ютерної графіки кінематографи бентежать уяву
глядача дивовижними образами і незвичайними
перевтіленнями на екрані.
Перетворення допомагають художникам
правильно будувати композиції картин , а хімікам –
досліджувати структуру кристалів. На цьому уроці ми
пригадаємо вже відомі вам основні види геометричних
перетворень на площині та познайомимося з деякими
новими. Але це буде нелегко.

3.

Через терни до зірок. У житті нічого не
дається задарма. Звичайно, якщо ви не
зловили удачу за хвіст. Терни -це дуже
колюча рослина, так ,уявіть, скільки потрібно
пробиратися через ці тернии (праця,невлдачі,
непорозуміння…), щоб добитися результату
який ви бажаєте(зірки).
Це величезна праця, люди все життя
домагаються бажаного. Є ті люди, які просто
пливуть за течією і нічого не роблять що б
жити краще.
Пам’ятаєте притчу про жаб? Одна
потонула склавши лапки, інша збила
масло і вибралася назовні. Так давайте
будемо йти через терни, збивати масло.
Але жити так, щоб соромно нам не було
і все у нас було. Отож, вперед!

4.

Через терни до зірок…

5.

Девіз уроку:
Працюй наполегливо,
Швидко, старанно,
Щоб кожна хвилина
Не втратилась марно.

6.

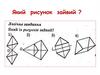
Терен №1

7.

Терен №1
Хто зайвий ?

8.

Терен № 2
“Згадати все”

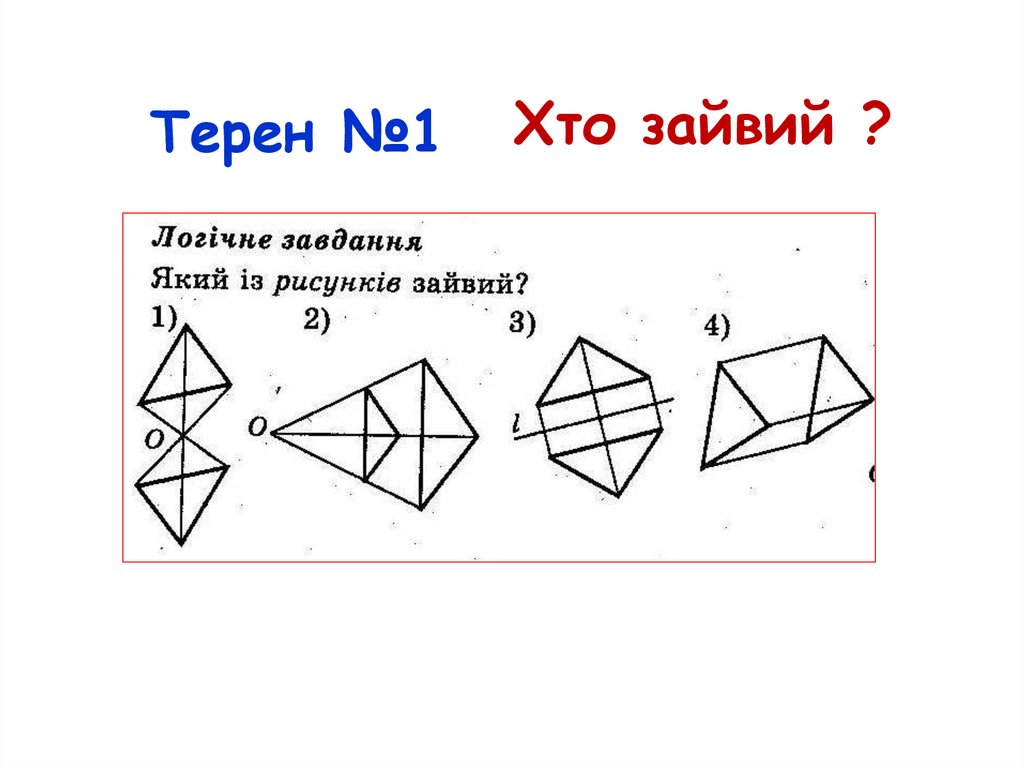
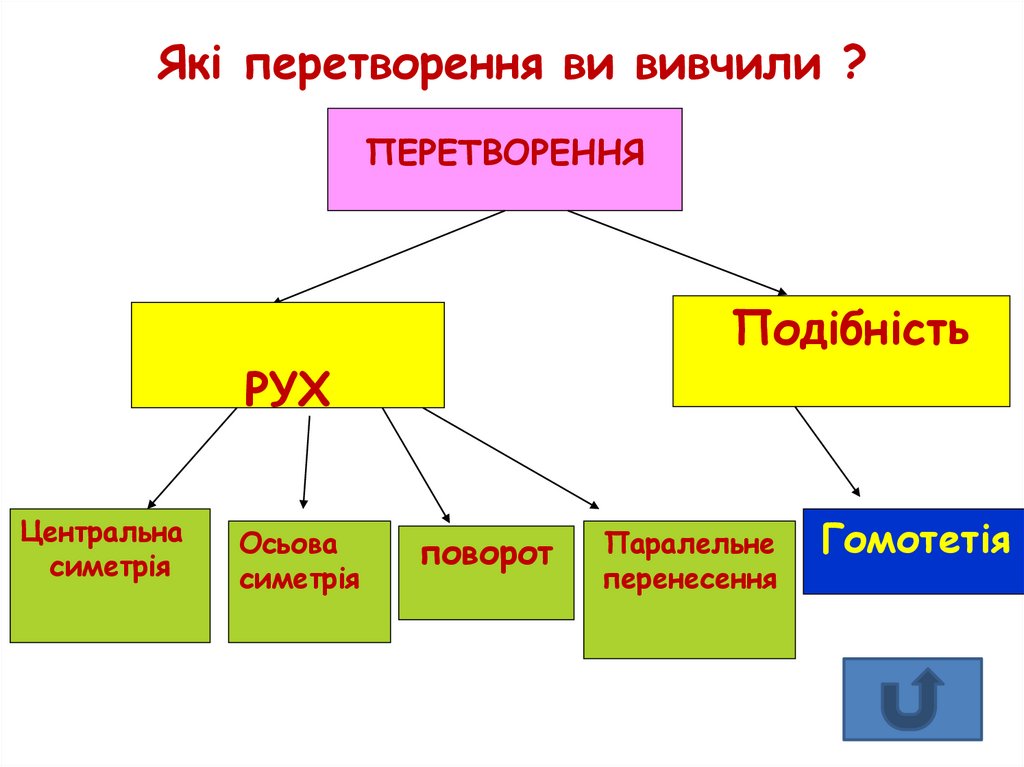
9. Які перетворення ви вивчили ?

ПЕРЕТВОРЕННЯ
???????????
РУХ
Центральна
симетрія
Осьова
симетрія
поворот
Паралельне
перенесення
???????

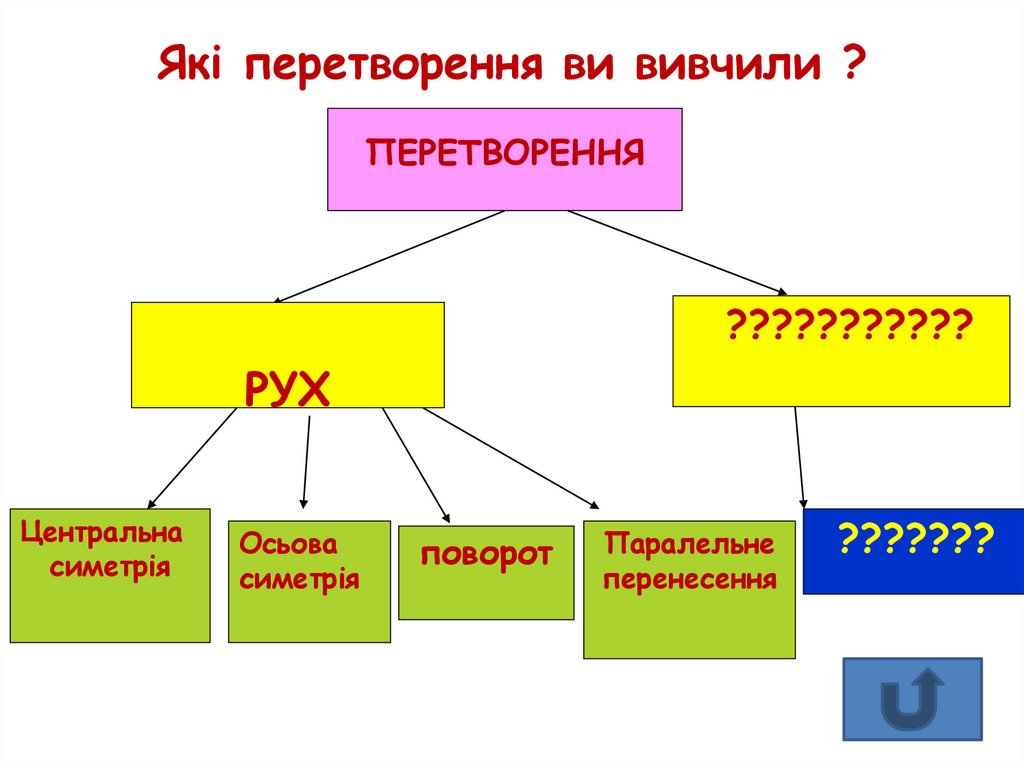
10. Перетворення фігур Рух

Симетрія
відносно точки
х
у1
у
о
х1
Симетрія
відносно
прямої
х
Поворот
відносно точки
на кут α
м
х1
х
Р
l
l
у
x
y
х1
о
Y
Паралельне
перенесення на
відстань l
у1
Y1
X1
y1
ОY1=ОУ
МХ1=МХ, РY1=РY
XX1 l, YY1 l
О–центр повороту
ХОХ1= YOY1=α,OX1
=OX, OY1=OY
l – напрямлений
вектор, ХХ1 l,
YY1 l, X1=YY1=l
Х1У1 = ХУ
Х1У1 = ХУ
Х1У1 = ХУ
Х1У1 = ХУ
О – центр симетрії
ОХ1=ОХ,
l – вісь симетрії,

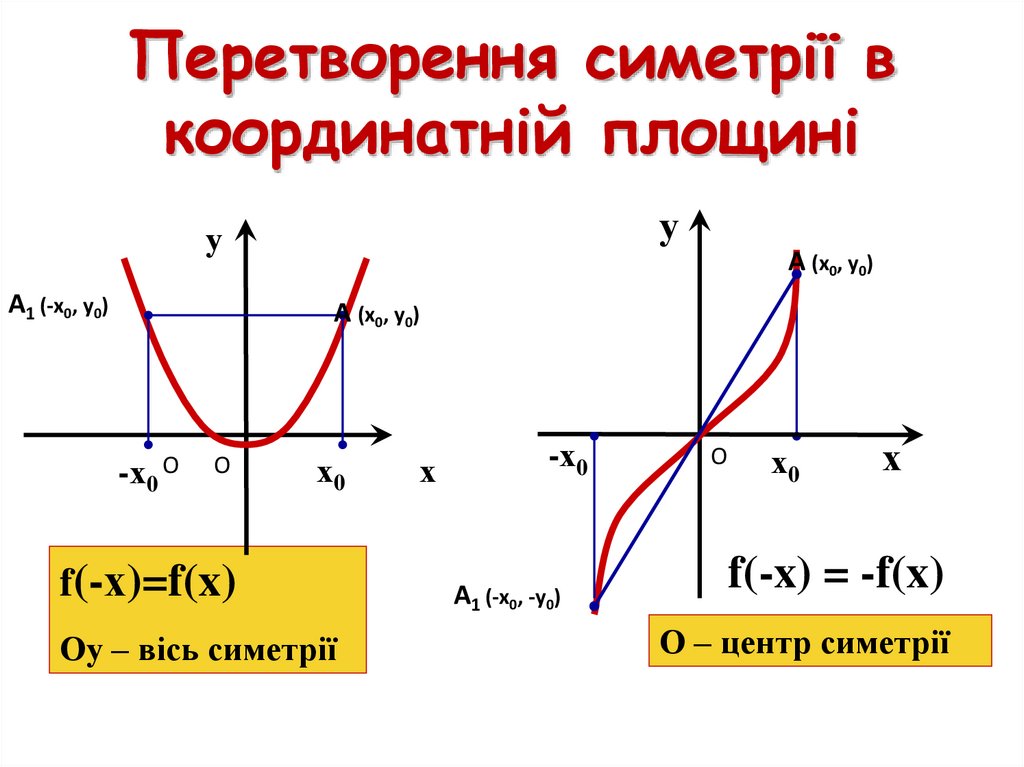
11. Перетворення симетрії в координатній площині

у
у
А1 (-х0, у0)
А (х0, у0)
А (х0, у0)
-х0 О
О
х0
f(-х)=f(x)
Оу – вісь симетрії
х
-х0
А1 (-х0, -у0)
О
х0
х
f(-x) = -f(x)
О – центр симетрії

12.

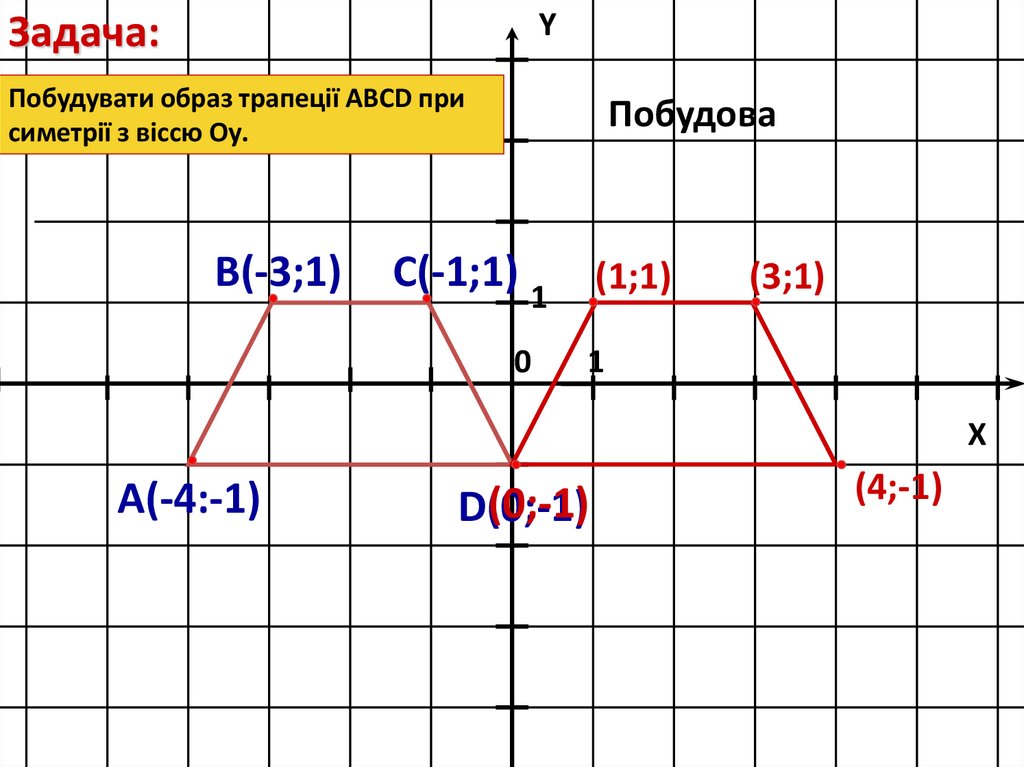
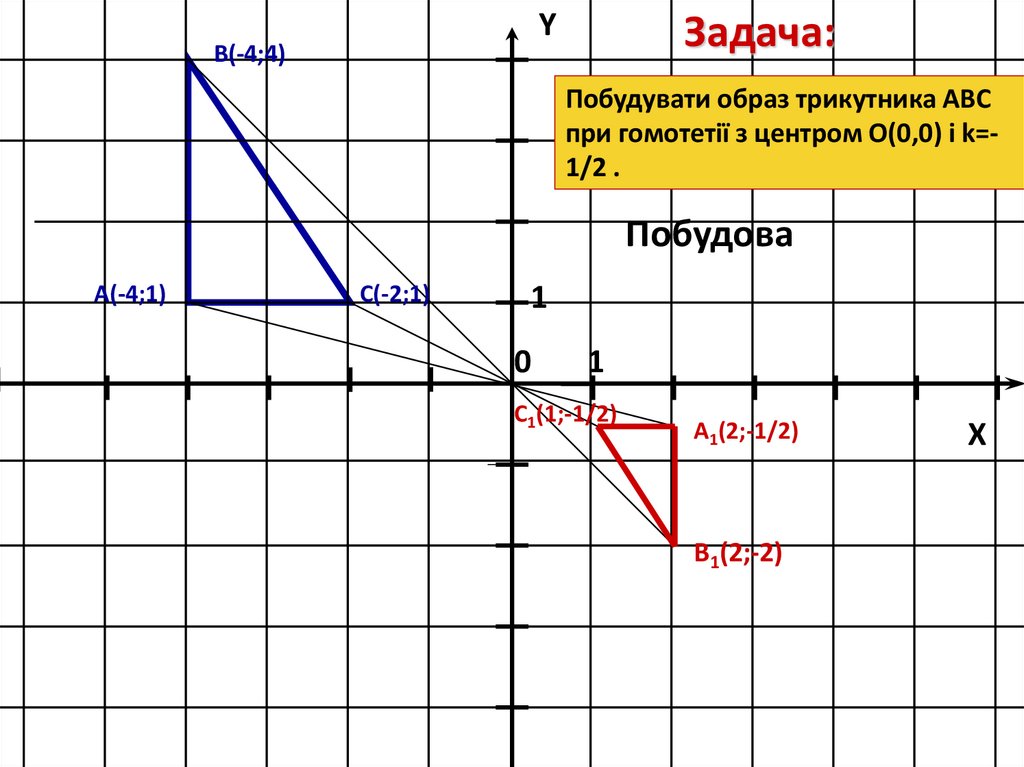
Y
Задача:
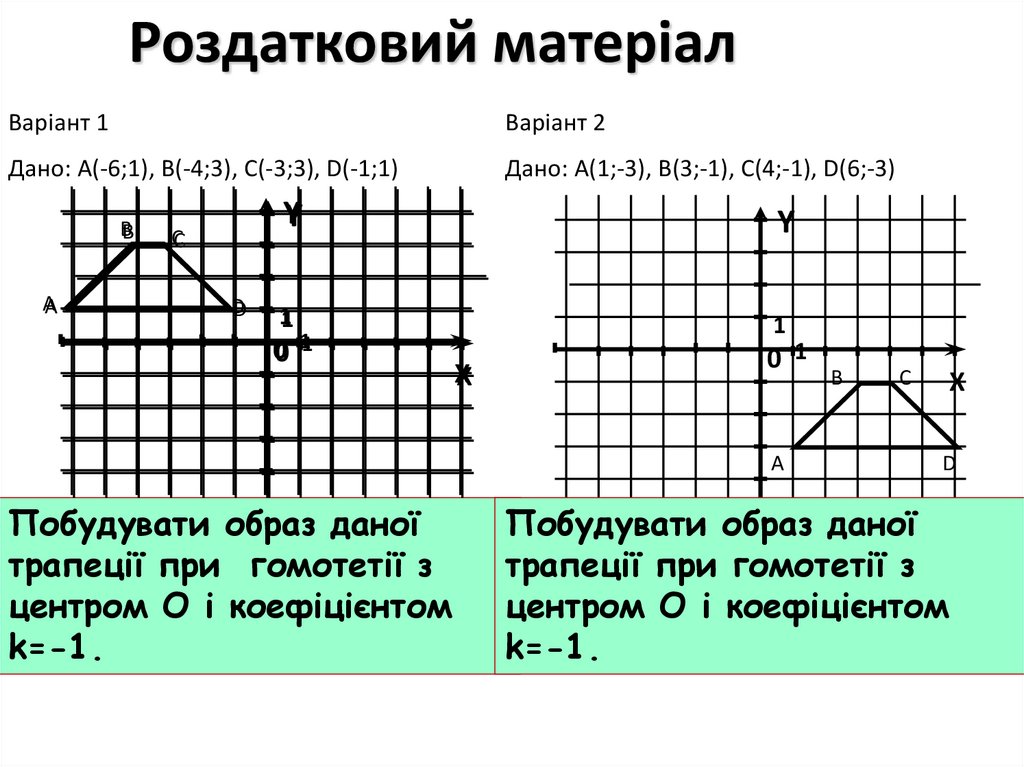
Побудувати образ трапеції ABCD при
симетрії з віссю Оу.
В(-3;1)
Побудова
С(-1;1) 1
0
(1;1)
(3;1)
1
X
А(-4:-1)
(0;-1)
D(0;-1)
(4;-1)

13.

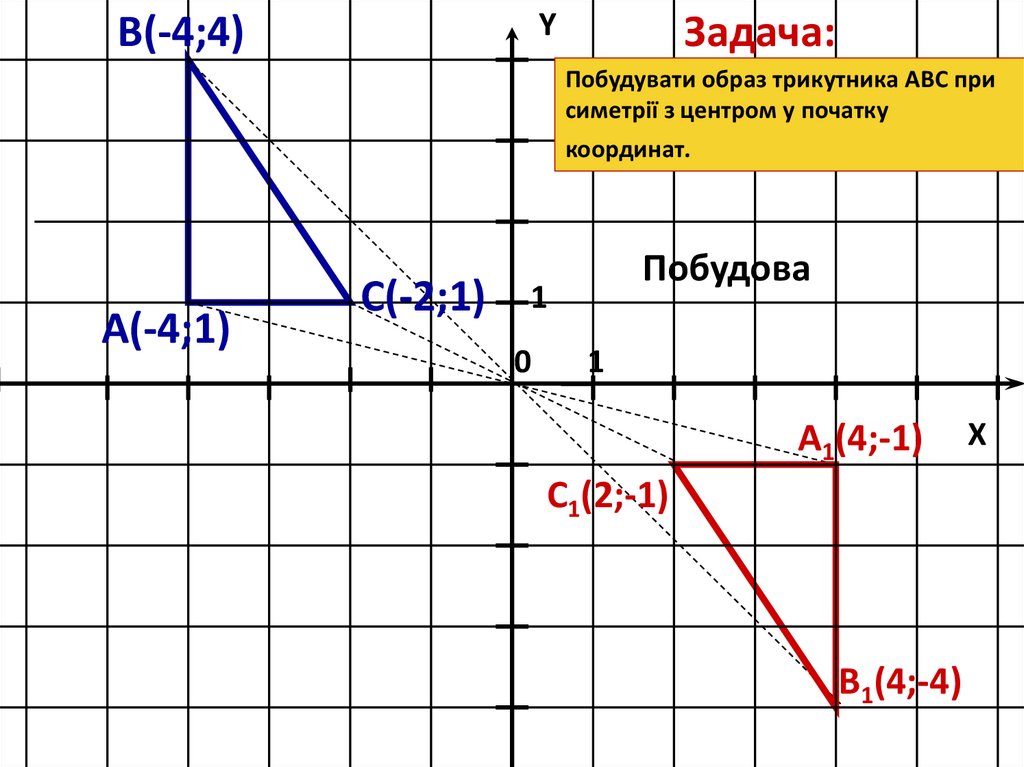
Y
В(-4;4)
Задача:
Побудувати образ трикутника АВС при
симетрії з центром у початку
координат.
А(-4;1)
С(-2;1)
Побудова
1
0
1
A1(4;-1)
C1(2;-1)
B1(4;-4)
X

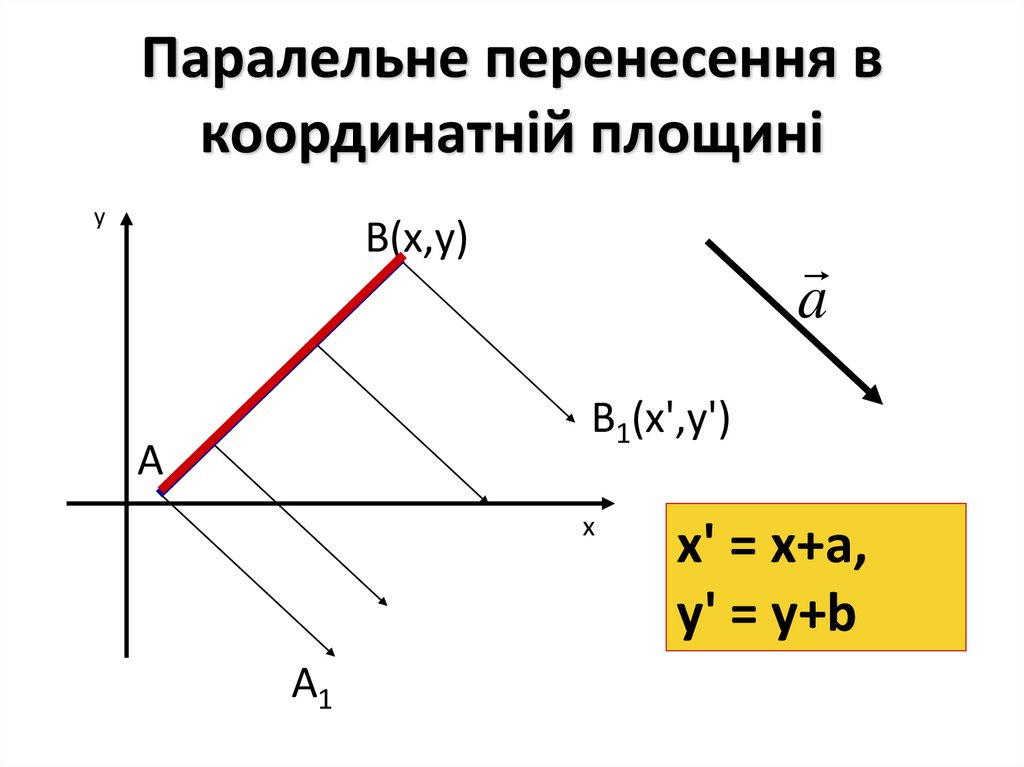
14. Паралельне перенесення в координатній площині

у
В(х,у)
a
В1(х',у')
А
х
А1
х' = х+а,
у' = у+b

15.

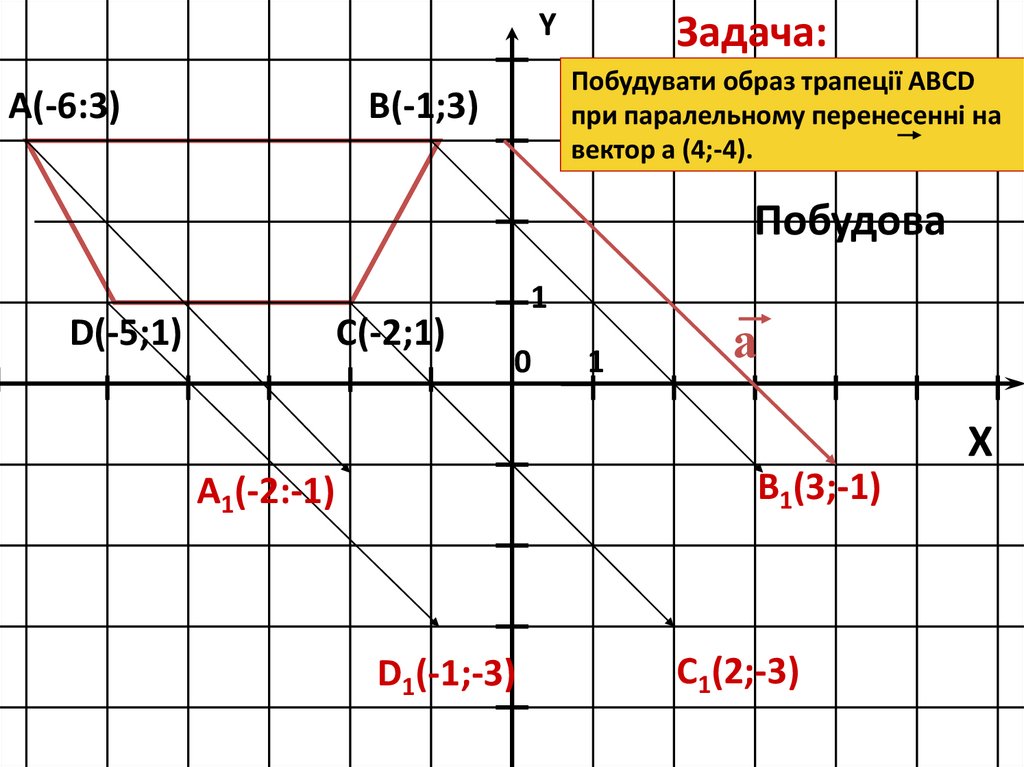
Y
А(-6:3)
Задача:
Побудувати образ трапеції ABCD
при паралельному перенесенні на
вектор a (4;-4).
В(-1;3)
Побудова
D(-5;1)
С(-2;1)
1
0
1
а
X
B1(3;-1)
A1(-2:-1)
D1(-1;-3)
C1(2;-3)

16.

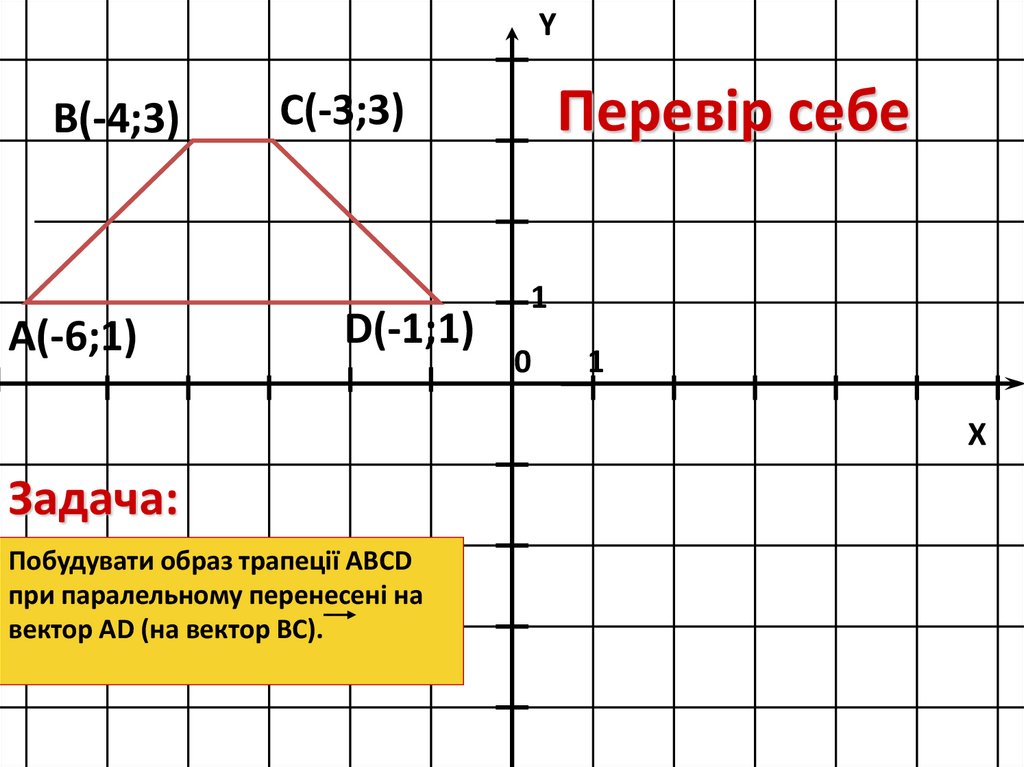
Y
В(-4;3)
А(-6;1)
Перевір себе
С(-3;3)
D(-1;1)
1
0
1
X
Задача:
Побудувати образ трапеції ABCD
при паралельному перенесені на
вектор АD (на вектор ВС).

17.

Y
В
А
С
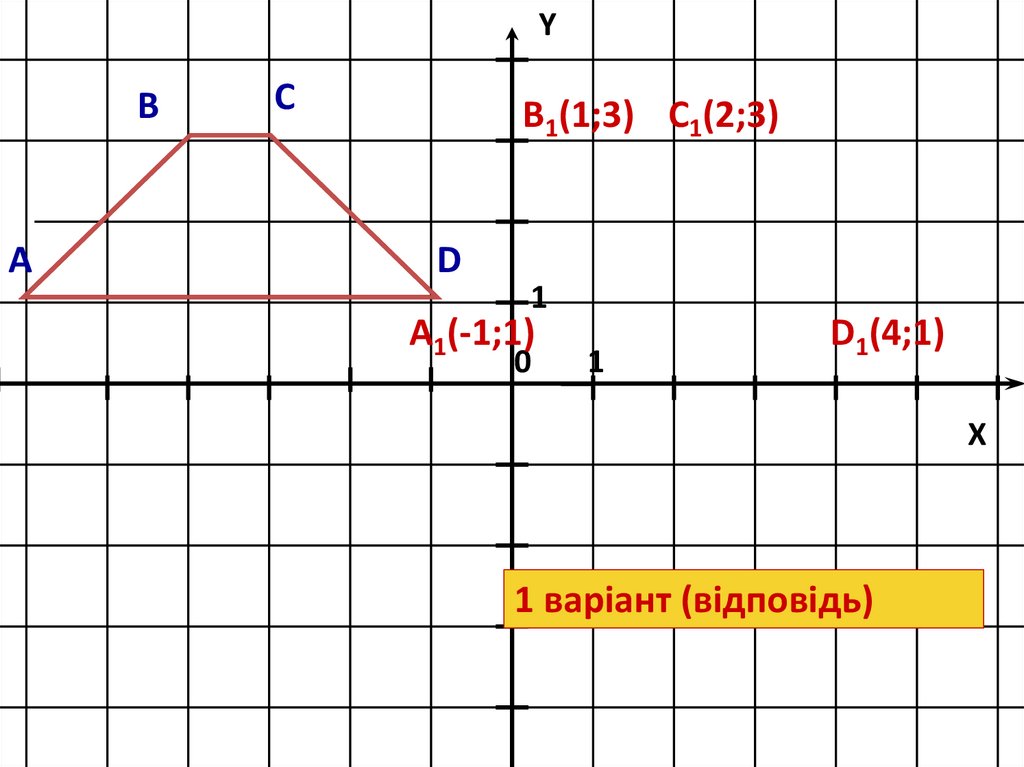
B1(1;3) C1(2;3)
D
1
A1(-1;1)
0
1
D1(4;1)
X
1 варіант (відповідь)

18.

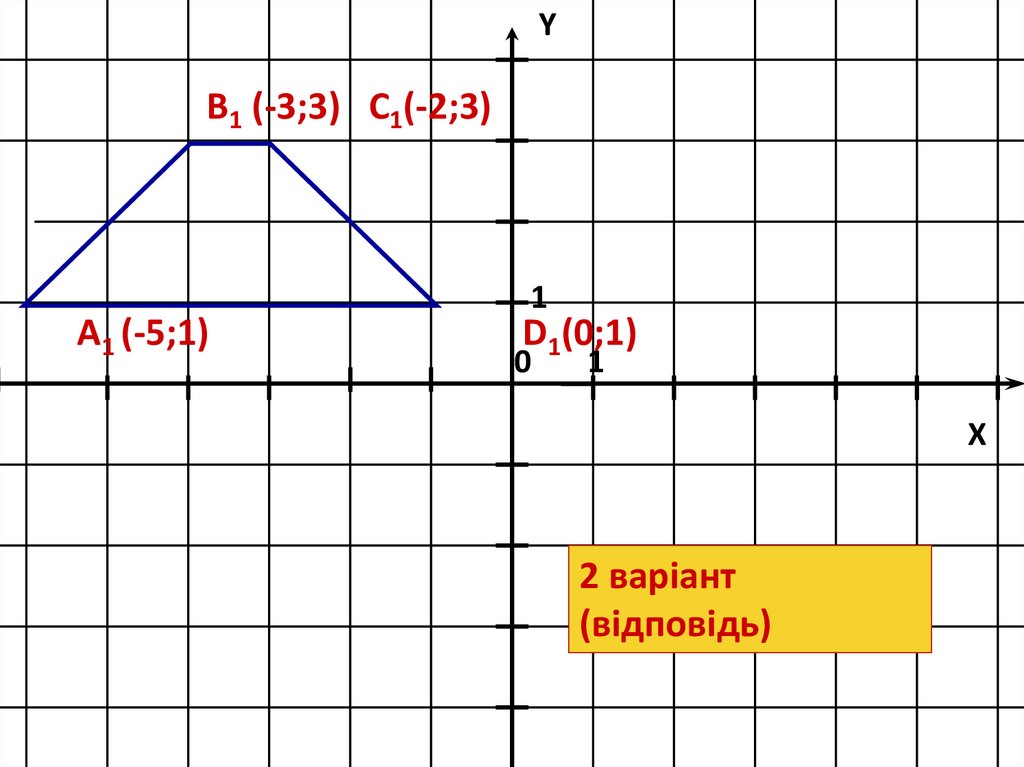
Y
B1 (-3;3) C1(-2;3)
A1 (-5;1)
1
D1(0;1)
0
1
X
2 варіант
(відповідь)

19.

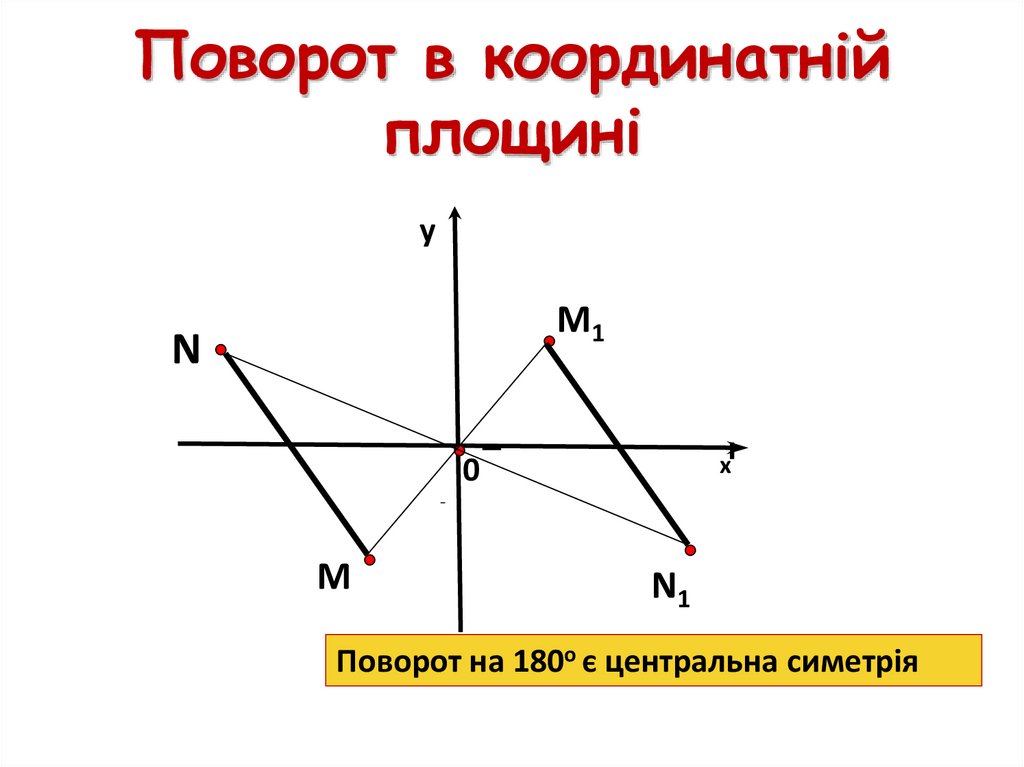
Поворот в координатній
площині
у
M1
N
х
0
M
N1
Поворот на 180о є центральна симетрія

20.

Y
B1(3;5)
A1(1;4)
В(-5;3)
С(-1;3)
D1(1;1)
1
А(-4:-1)
D(-1;1)
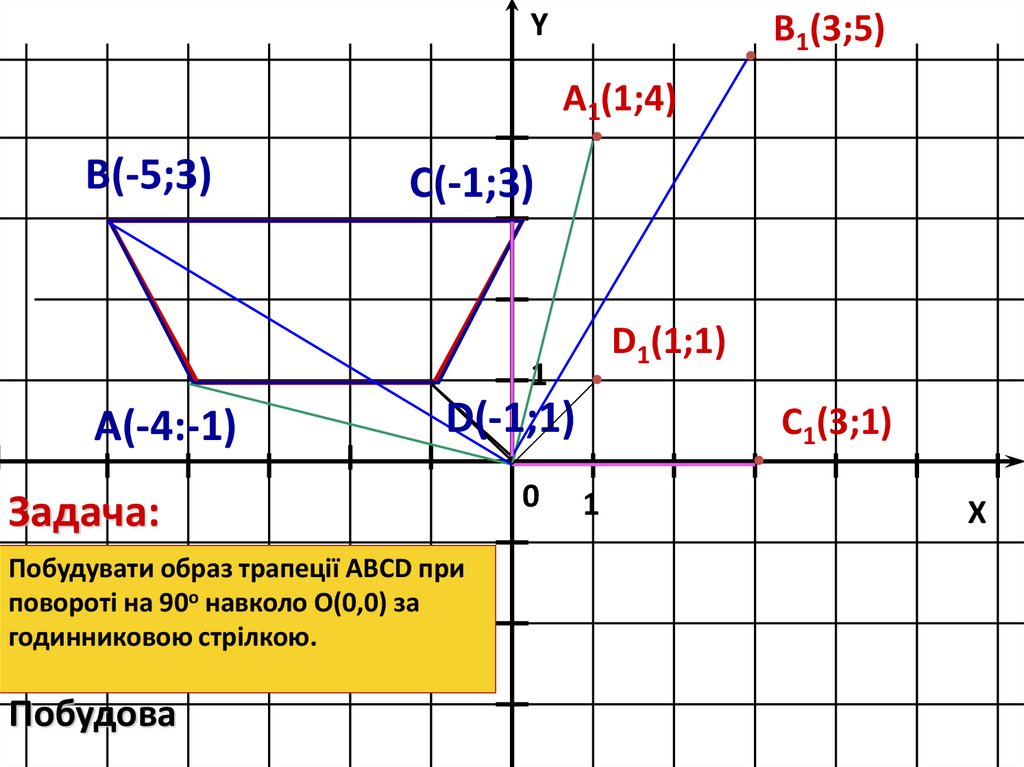
Задача:
Побудувати образ трапеції АВСD при
повороті на 90о навколо О(0,0) за
годинниковою стрілкою.
Побудова
0
C1(3;1)
1
X

21.

Терен №3
“Спробуй
зрозумій”

22.

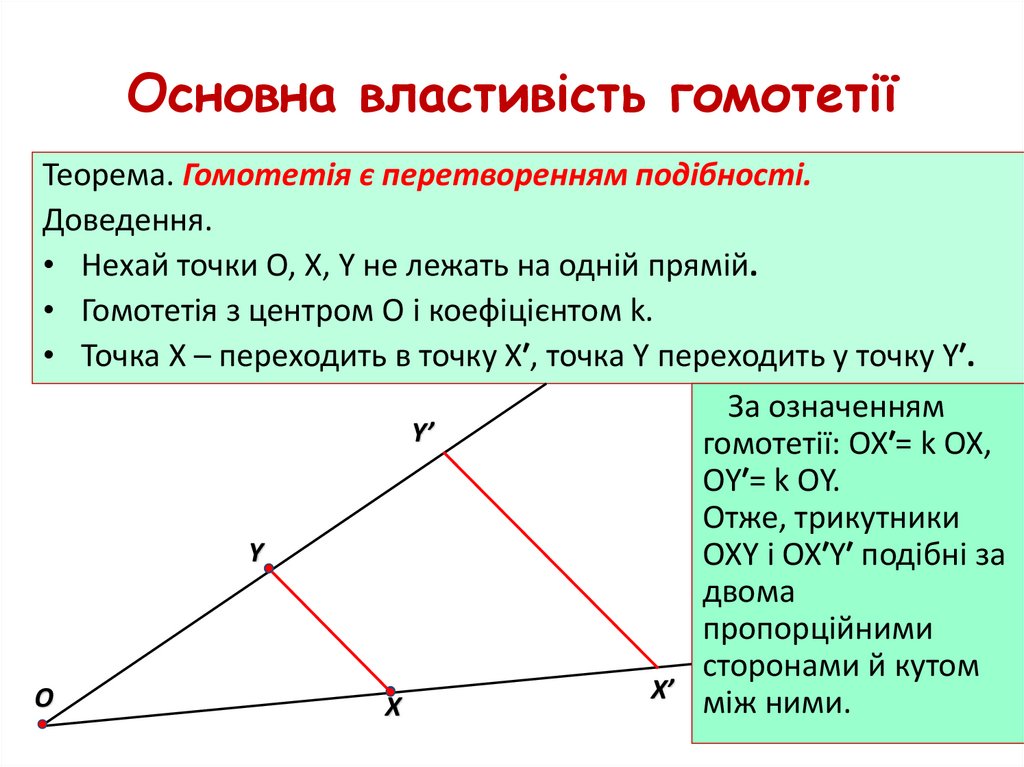
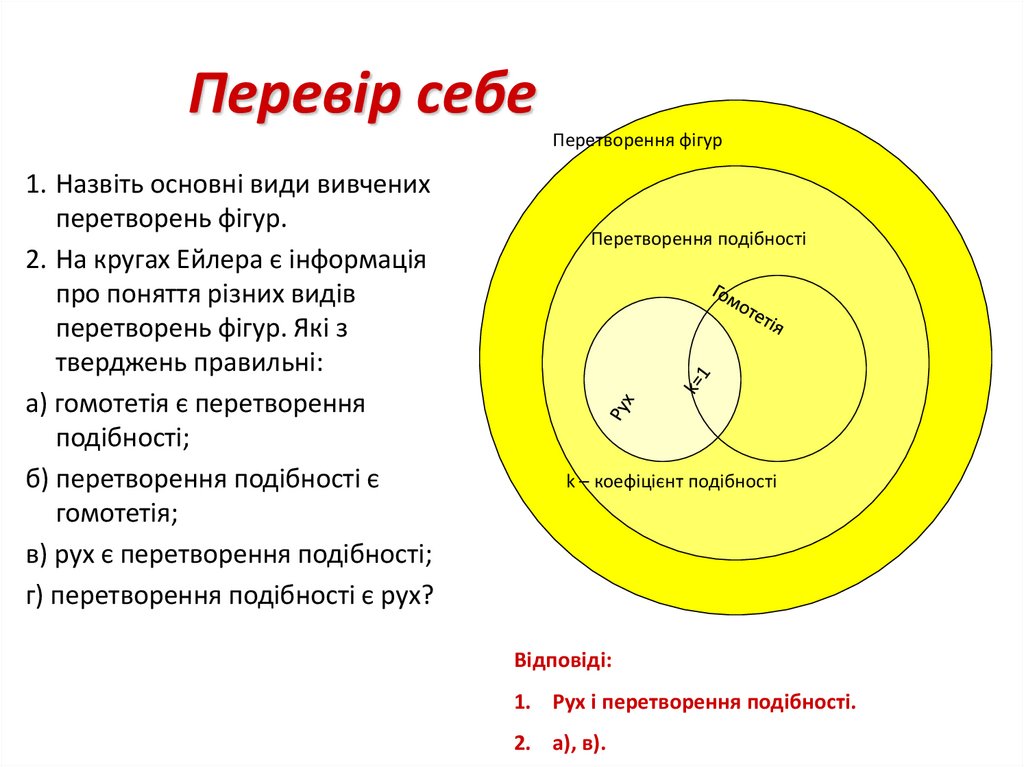
Що ж таке ???????

23. Тема уроку: Перетворення подібності. Гомотетія

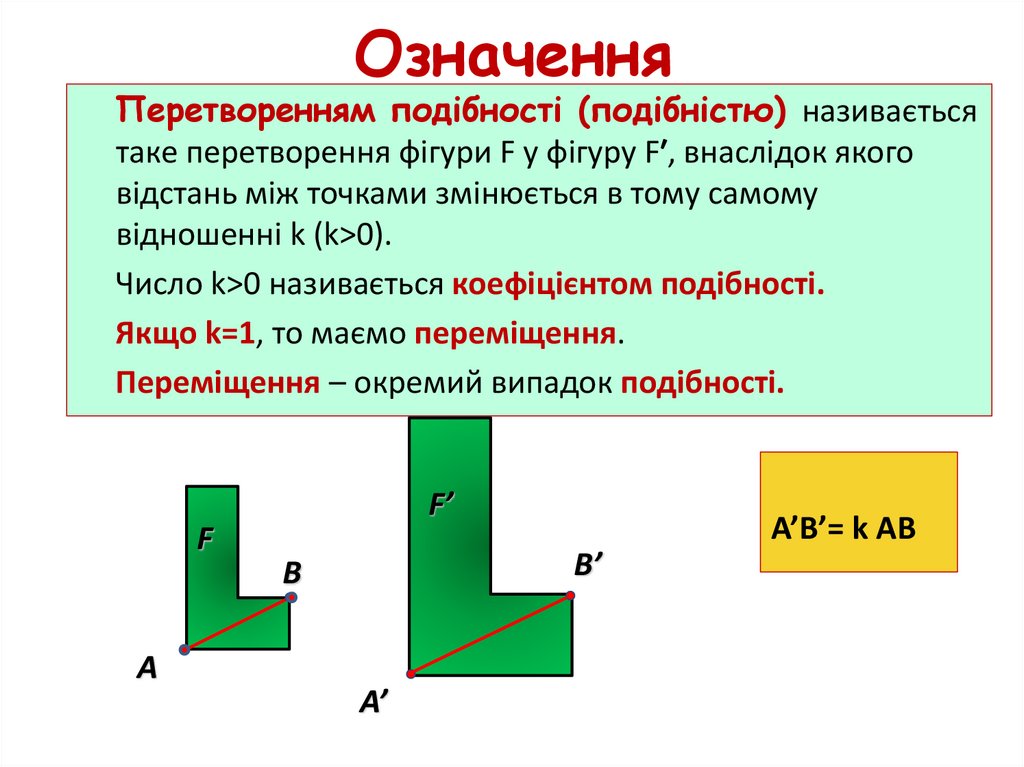
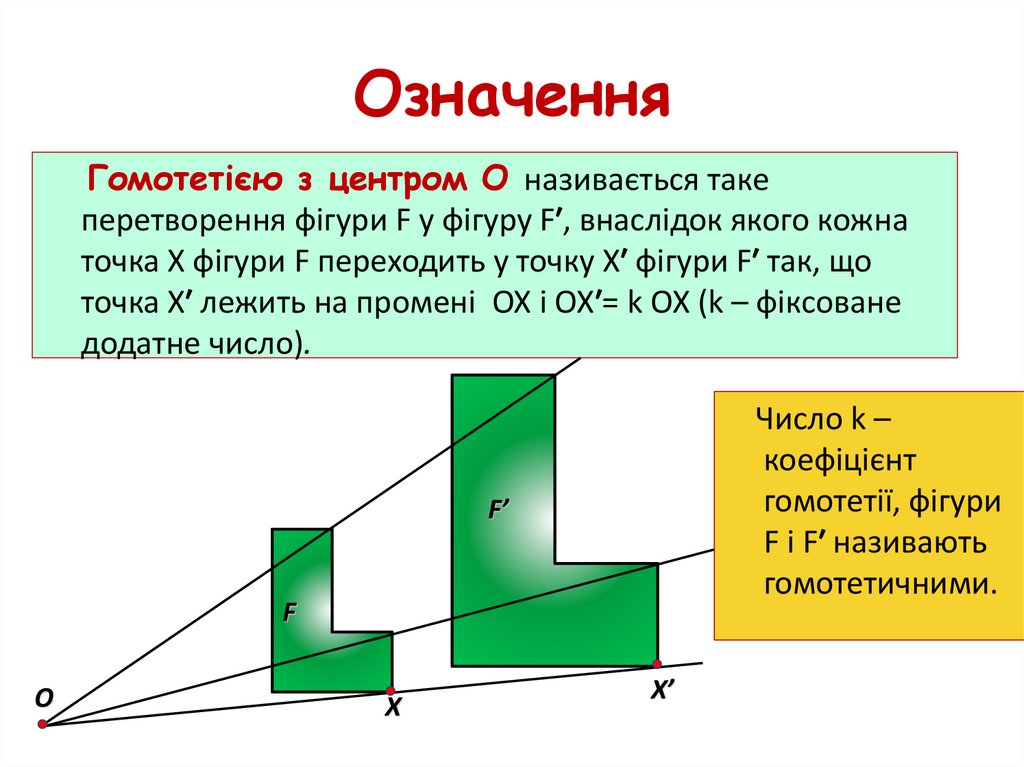
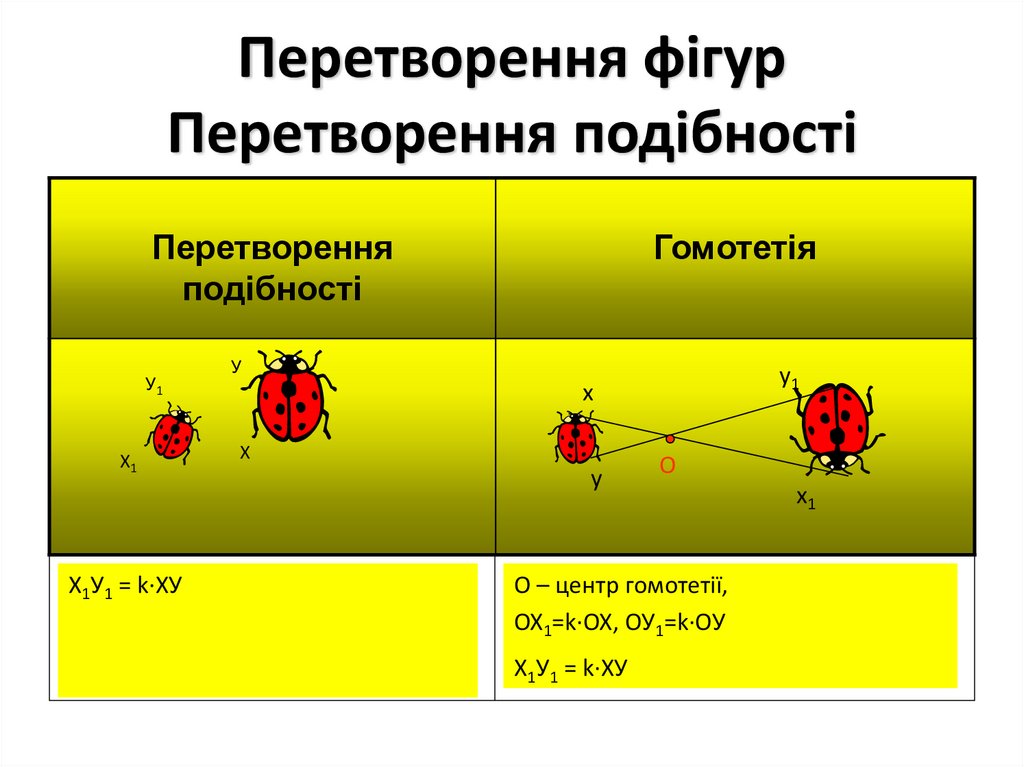
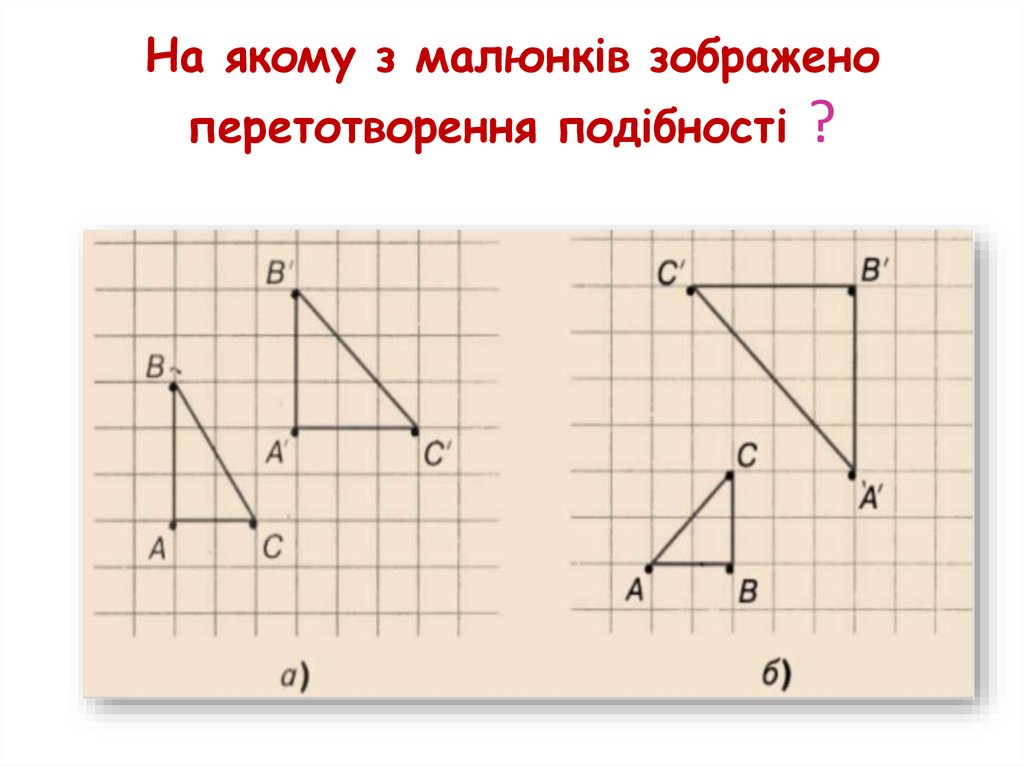
24. Означення

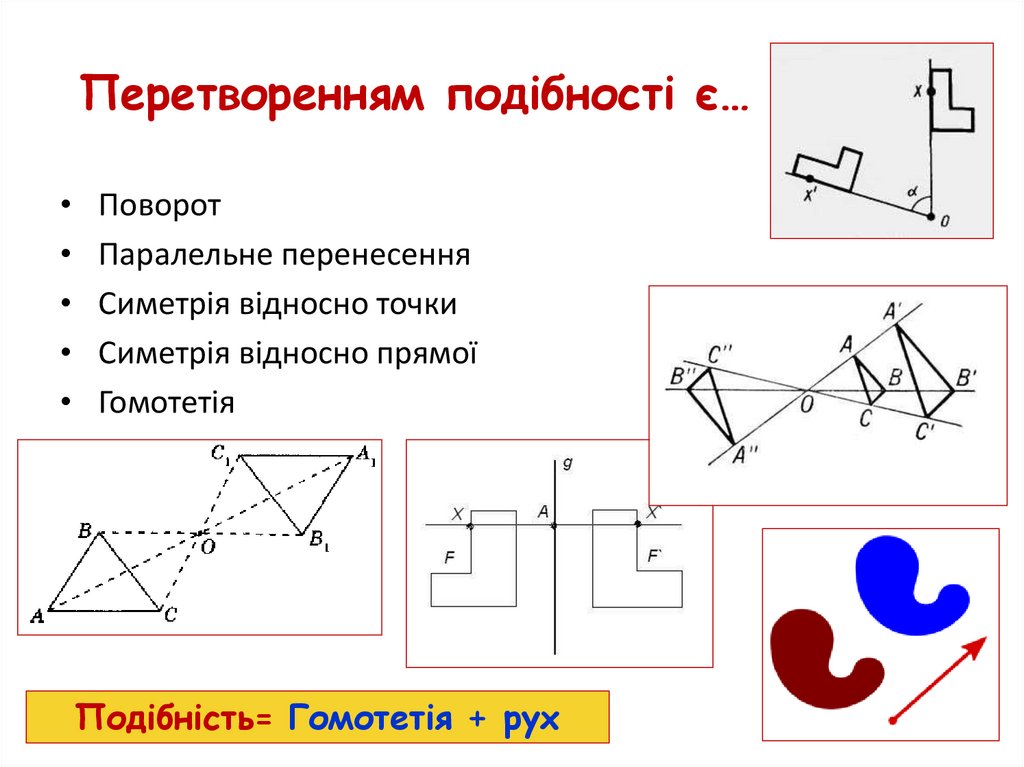
Перетворенням подібності (подібністю) називається
таке перетворення фігури F у фігуру F′, внаслідок якого
відстань між точками змінюється в тому самому
відношенні k (k>0).
Число k>0 називається коефіцієнтом подібності.
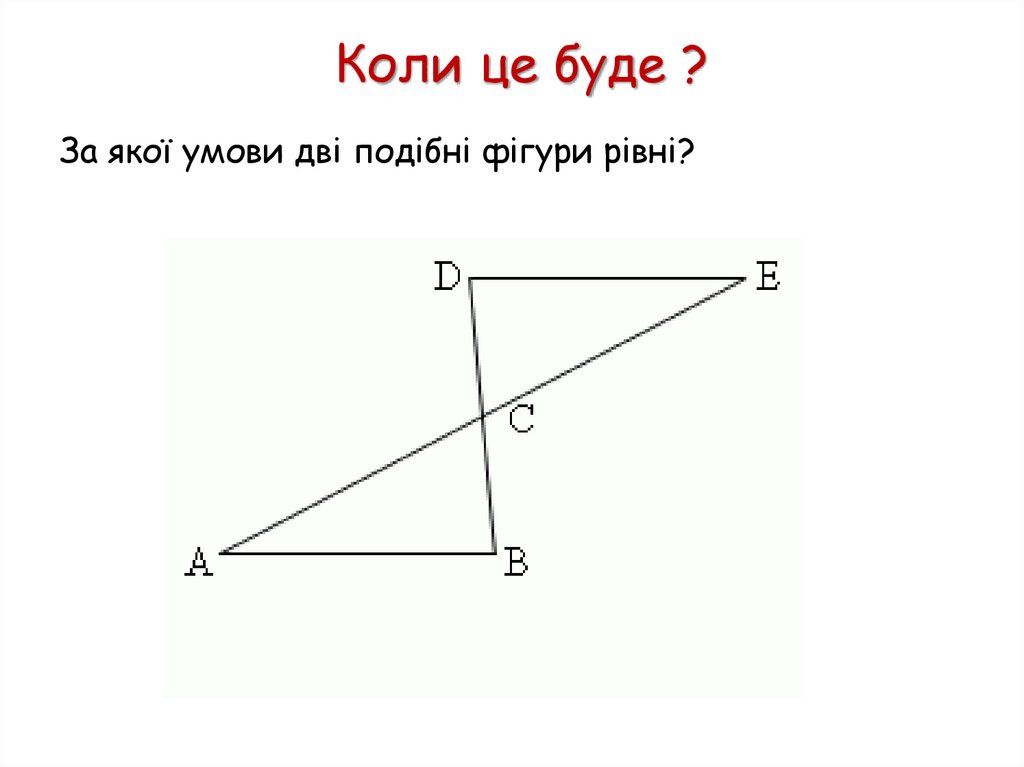
Якщо k=1, то маємо переміщення.
Переміщення – окремий випадок подібності.
F’
F
A
A’B’= k AB
B’
B
A’

25.

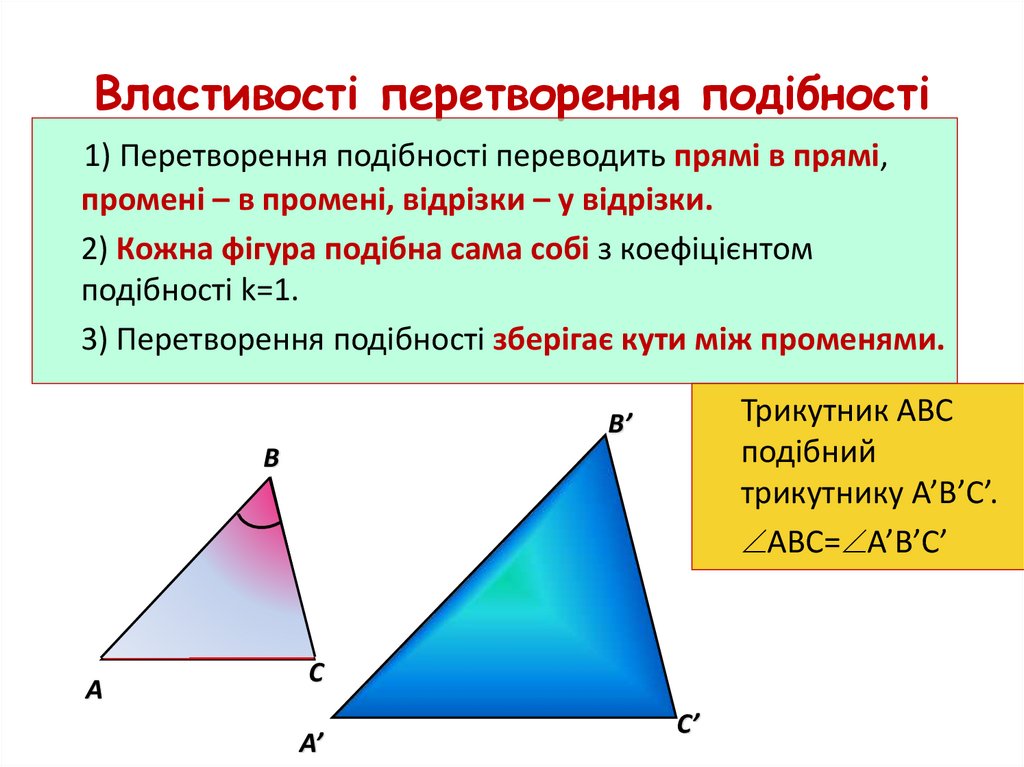
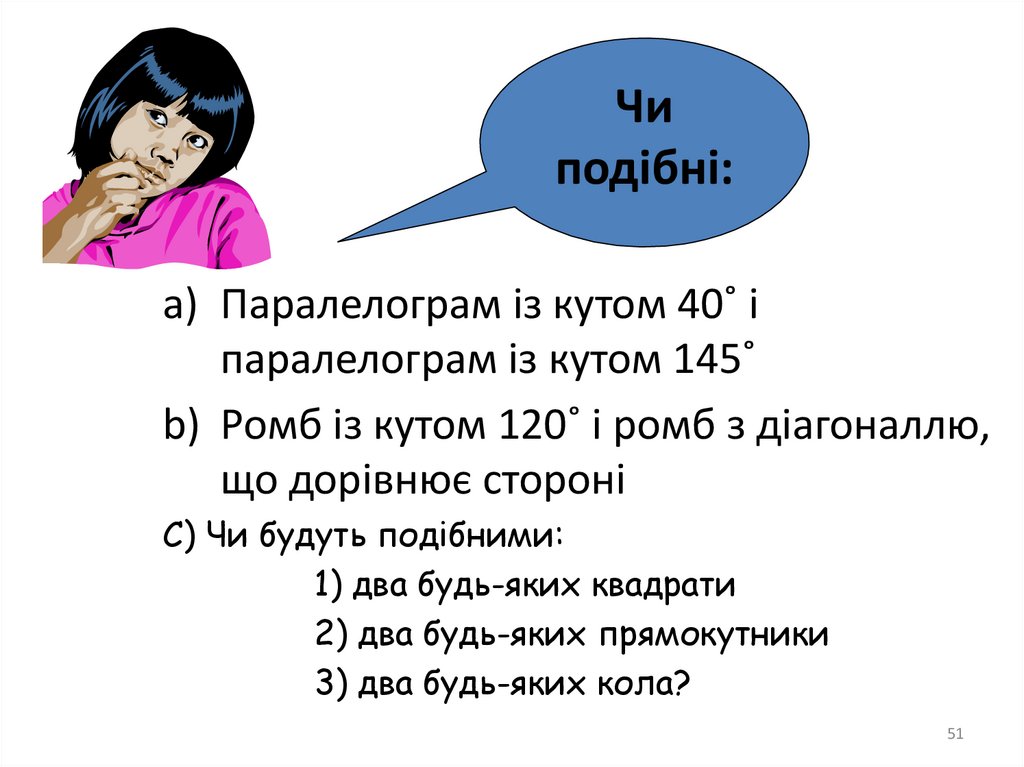
Які ж властивості має
перетворення подібності ?

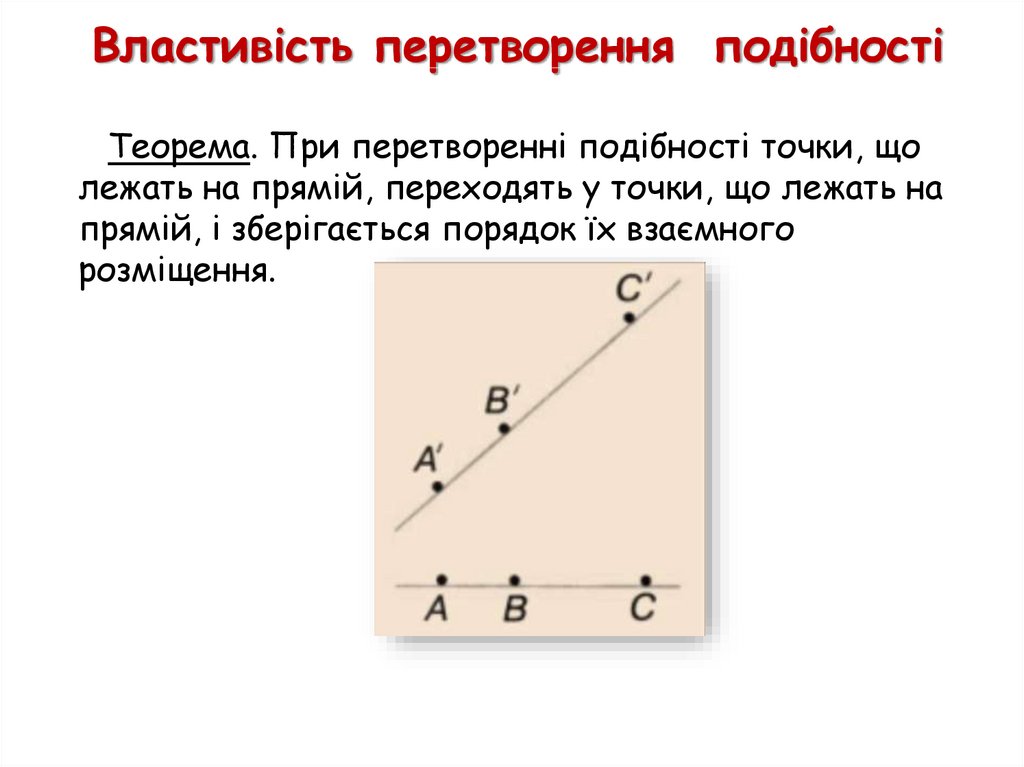
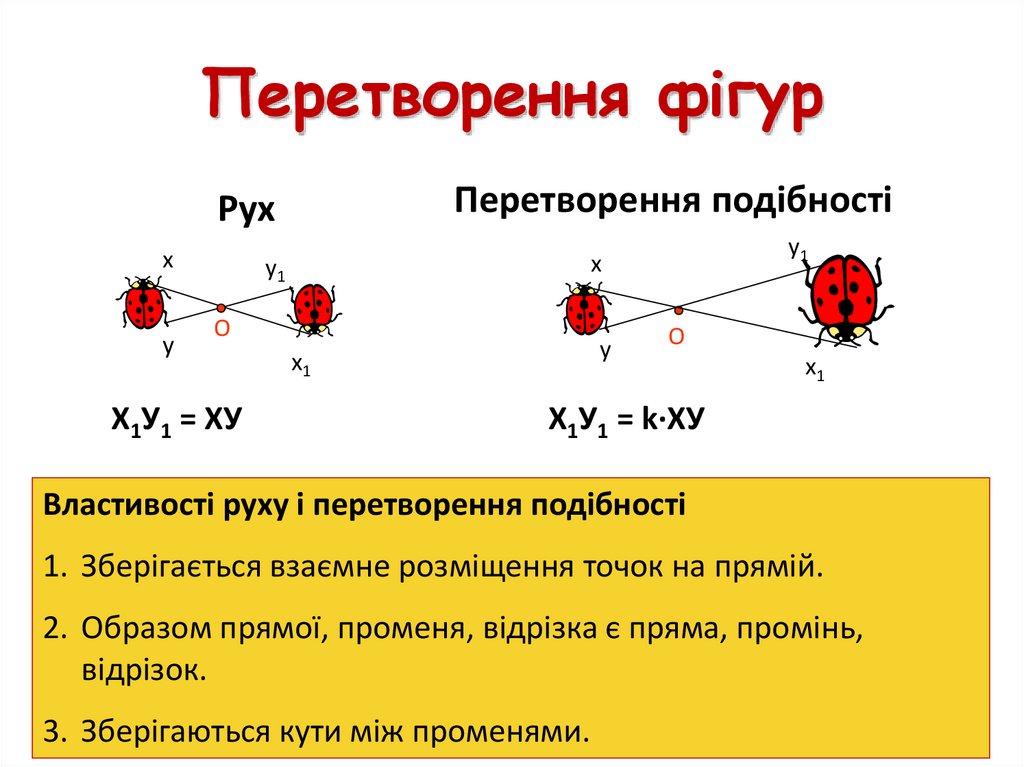
26. Властивість перетворення подібності

Теорема. При перетворенні подібності точки, що
лежать на прямій, переходять у точки, що лежать на
прямій, і зберігається порядок їх взаємного
розміщення.

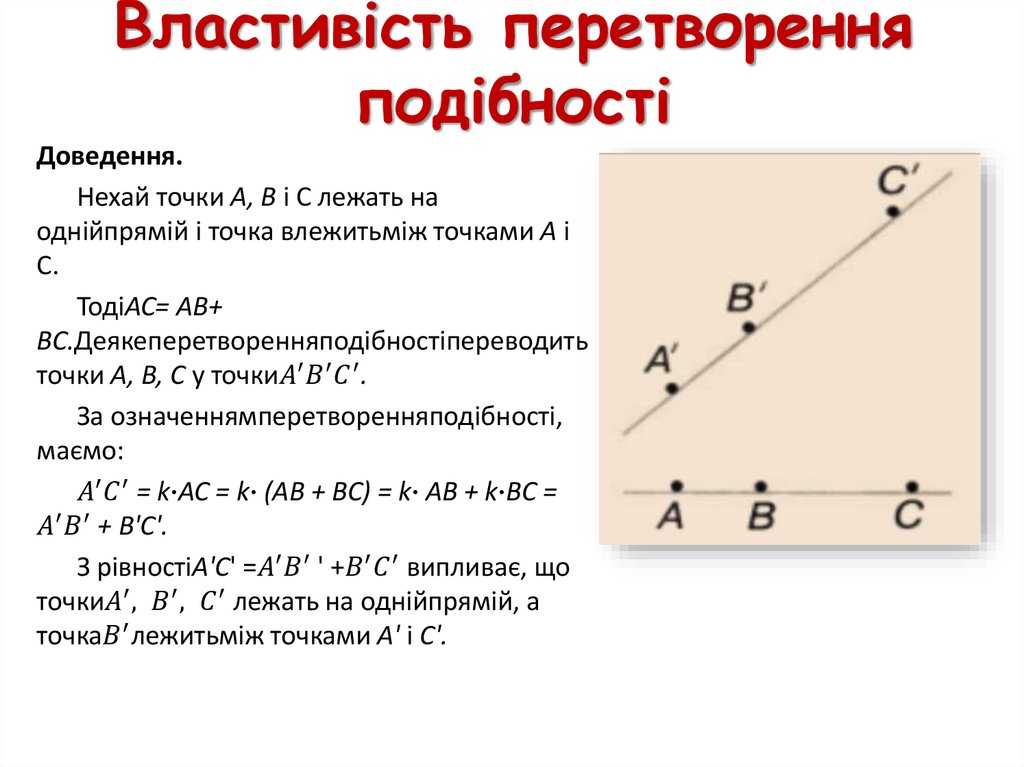
27. Властивість перетворення подібності

Доведення.
Нехай точки А, В і С лежать на
однійпрямій і точка влежитьміж точками А і
С.
ТодіАС= АВ+
ВС.Деякеперетворенняподібностіпереводить
точки А, В, С у точки