Похожие презентации:
Наноэлектроника
1.
НАНОЭЛЕКТРОНИКАпрофессор
Борисенко Виктор Евгеньевич
Лекции - 48 часов
Самостоятельная управляемая работа - 16 часов
Лабораторные работы - 16 часов
Экзамен
Курсовой проект (НТНМ)
Белорусский государственный университет информатики и радиоэлектроники
2.
СОДЕРЖАНИЕ ДИСЦИПЛИНЫРаздел 1. Физические основы наноэлектроники
Раздел 2. Методы формирования наноразмерных
структур (нанотехнологии)
Раздел 3. Перенос носителей заряда в
низкоразмерных структурах и приборы
на их основе
3.
ЛИТЕРАТУРАВ. Е. Борисенко, А. И. Воробьева,
А.Л. Данилюк, Е. А. Уткина
НАНОЭЛЕКТРОНИКА
(Бином, Москва, 2013)
V. E. Borisenko, S. Ossicini
What is What in the Nanoworld
(Wiley-VCH, Weinheim, 2012)
4.
Наноэлектроника (nanoelectronics)это область науки и техники,
занимающаяся созданием, исследованием
и применением электронных приборов с
нанометровыми размерами элементов
элементов, в
основе функционирования которых лежат
эффекты.
квантовые эффекты
5.
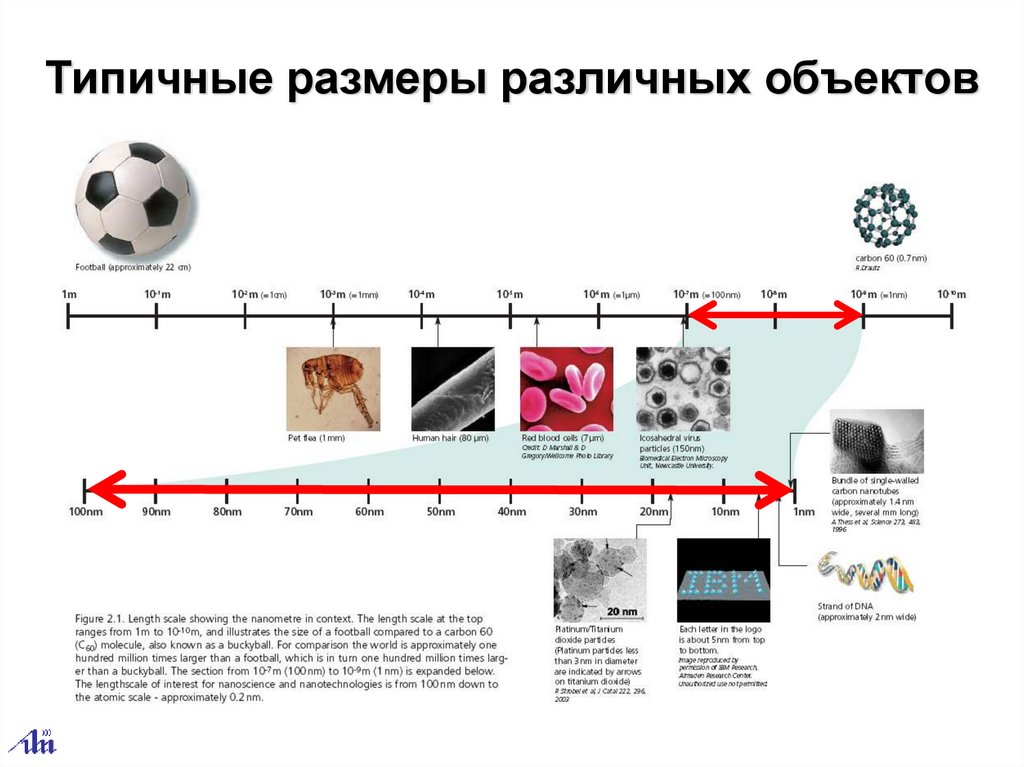
Типичные размеры различных объектов6.
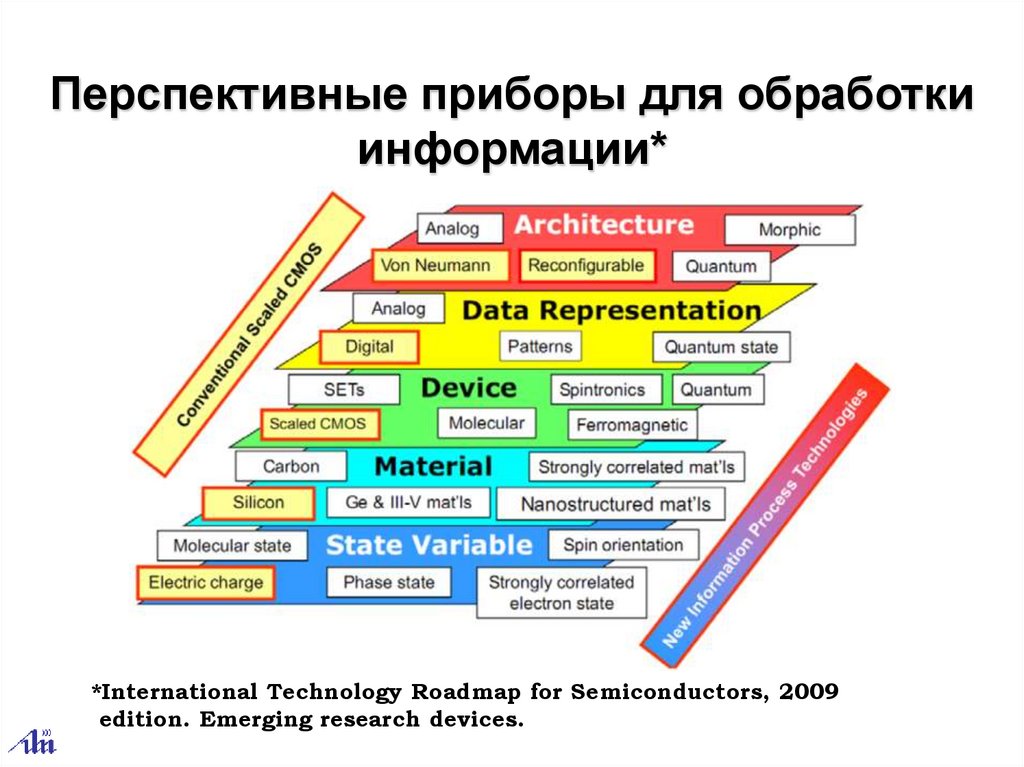
Перспективные приборы для обработкиинформации*
*International Technology Roadmap for Semiconductors, 2009
edition. Emerging research devices.
7.
Перспективные приборы и технологииобработки информации
https://pubs.rsc.org/en/content/articlelanding/2015/NR/C4NR01600A#!divAbstract
8.
Наномедицинаhttps://www.pinterest.com/pin/105553184993799249/
9.
1. Физические основы наноэлектроники1.1.
Фундаментальные явления
в низкоразмерных
структурах
1.1.1. Квантовое ограничение
1.1.2. Баллистический транспорт носителей заряда
1.1.3. Туннелирование носителей заряда *
1.1.4. Спиновые эффекты*
1.2.
Элементы низкоразмерных
структур
1.2.1. Свободная поверхность и межфазные границы
1.2.2. Сверхрешетки
1.2.3. Моделирование атомных конфигураций
1.3.
Структуры с квантовым
ограничением внутренним
электрическим полем
1.3.1. Квантовые колодцы*
1.3.2. Модуляционно-легированные структуры*
1.3.3. Дельта-легированные структуры*
1.4.
Структуры с квантовым
ограничением внешним
электрическим полем
1.4.1. Структуры металл/диэлектрик/полупроводник*
1.4.2. Структуры с расщепленным затвором*
* темы для самостоятельного изучения
10.
1.1. Фундаментальные явления в низкоразмерныхструктурах
1.1.1. Квантовое ограничение (quantum confinement)
1
2
2
2
2
E
px p y pz
k x2 k y2 k z2
2m *
2m *
free electrons:
confined electrons:
n=3
E3
U(x)
n=2
E2
n = 2a/n (n = 1, 2, ...)
kn = 2 / n = n /a
2 k n2 2 2 n 2
En
2m * 2m * a 2
Y(x)
n=1
0
E1
0
a
x
2 2
E1
2m * a 2
11.
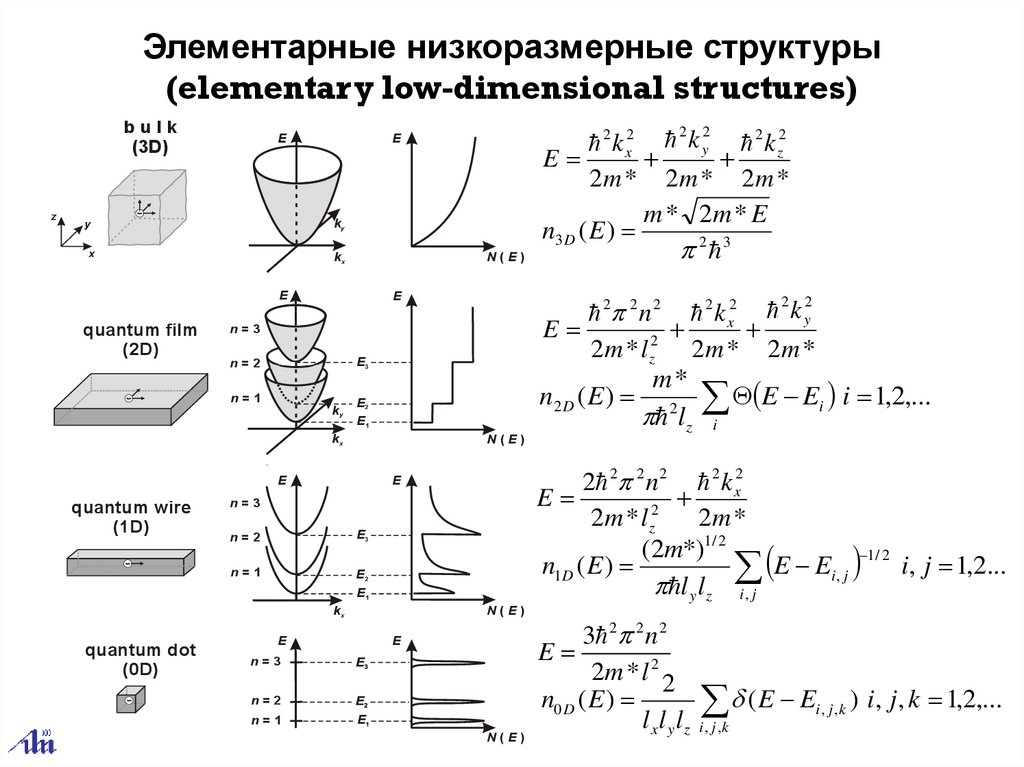
Элементарные низкоразмерные структуры(elementary low-dimensional structures)
b
bu
u ll k
k
b(3D)
ulk
(3D)
(3D)
z
z
z
E
E
E
E
E
E
k
kyyy
ky
k
kxxx
k
kx
y
y
y
x
x
x
x
N(E)
E
E
E
quantum
quantum film
film
quantum
film
(2D)
(2D)
(2D)
E
E
E
E
E33
E3
n
n=
=2
2
n=2
n
=3
n
n=
=3
3
n=3
k
kyy
ky
k
kxxx
kx
E
E
E
E
n
=2
n
n=
=2
2
n=2
E
3
E
E33
E3
n
=
n
=1
1
n
n=
=1
1
E
2
E
2
E
2
E
21
E
E
1
E
E11
E
E
E
E
E
E11
E11
E
2
2 2 2 n 2 2 k x2
E
2
2m * l z
2m *
(2m*)1/ 2
1/ 2
n1D ( E )
E Ei , j
i, j 1,2...
l y l z i , j
N
N (( E
E ))
N
N (( E
E ))
E
E
E
E
n
=
3
n=3
n
=
3
n=3
n
n=
=2
2
n
=
2
n
=
2
n
=
n=1
1
n
=
n=1
1
N (( E
E ))
N
N(E)
E
E
E
E
k
x
k
x
k
kxx
quantum
dot
quantum
dot
quantum
dot
quantum
dot
(0D)
(0D)
(0D)
(0D)
E
E22
E
E
E2111
E1
2 2 n 2 2 k x2 k y
E
2m * l z2 2m * 2m *
m*
n 2 D ( E ) 2 E Ei i 1,2,...
l z i
2
n
n=
=3
3
n=3
n
n=
=1
1
n=1
quantum
quantum wire
wire
quantum
wire
(1D)
(1D)
(1D)
(1D)
2 2
2 k x2 k y 2 k z2
E
2m * 2m * 2m *
m * 2m * E
n3 D ( E )
N
2 3
N ((( E
E )))
N
E
N
N (( E
E ))
N(E)
3 2 2 n 2
E
2m * l 2 2
n0 D ( E )
( E Ei , j ,k ) i, j, k 1,2,...
l xl y l z i , j ,k
12.
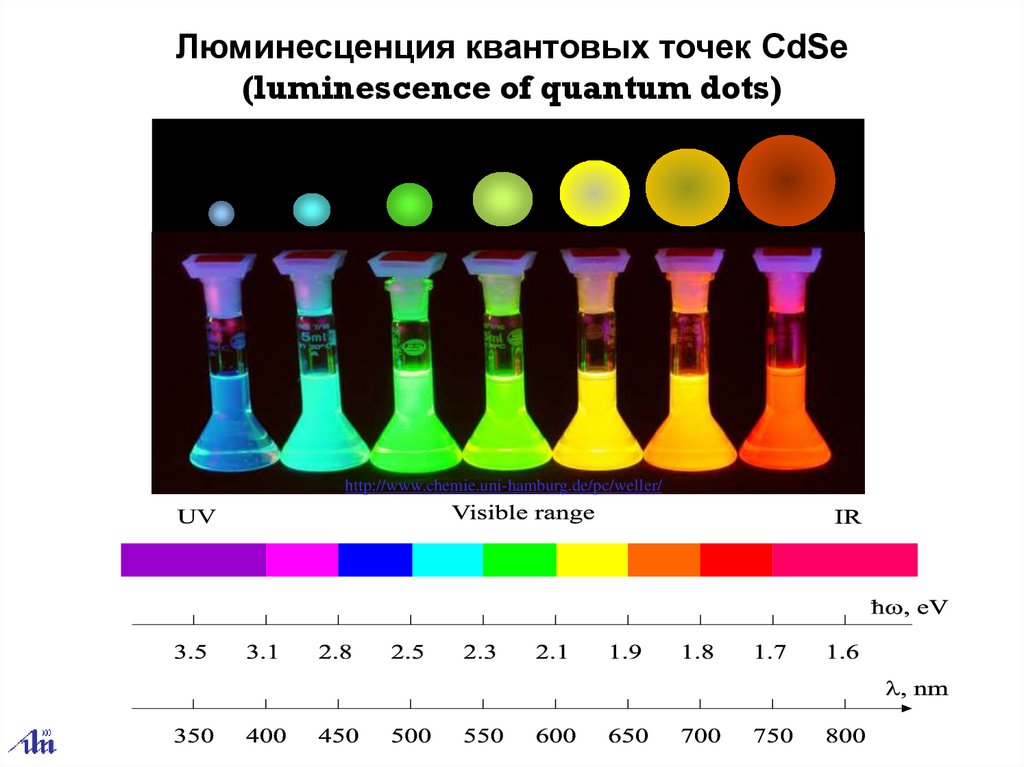
Люминесценция квантовых точек CdSe(luminescence of quantum dots)
http://www.chemie.uni-hamburg.de/pc/weller/
13.
1.1.2. Баллистический транспорт носителей заряда(ballistic transport)
EF → vF = (2EF/m*)1/2, kF = (2m*EF)1/2/ħ , F = 2 /kF
средняя длина свободного пробега
при упругом рассеянии
le = vF sc
средняя длина свободного пробега
при неупругом рассеянии
lin = vF
длина фазовой когерентности
l = (D )1/2
sc = Dd/vF2
f
f
vgrad r f agrad v f
t
t coll
f f0
f
t coll
кинетическое уравнение Больцмана
14.
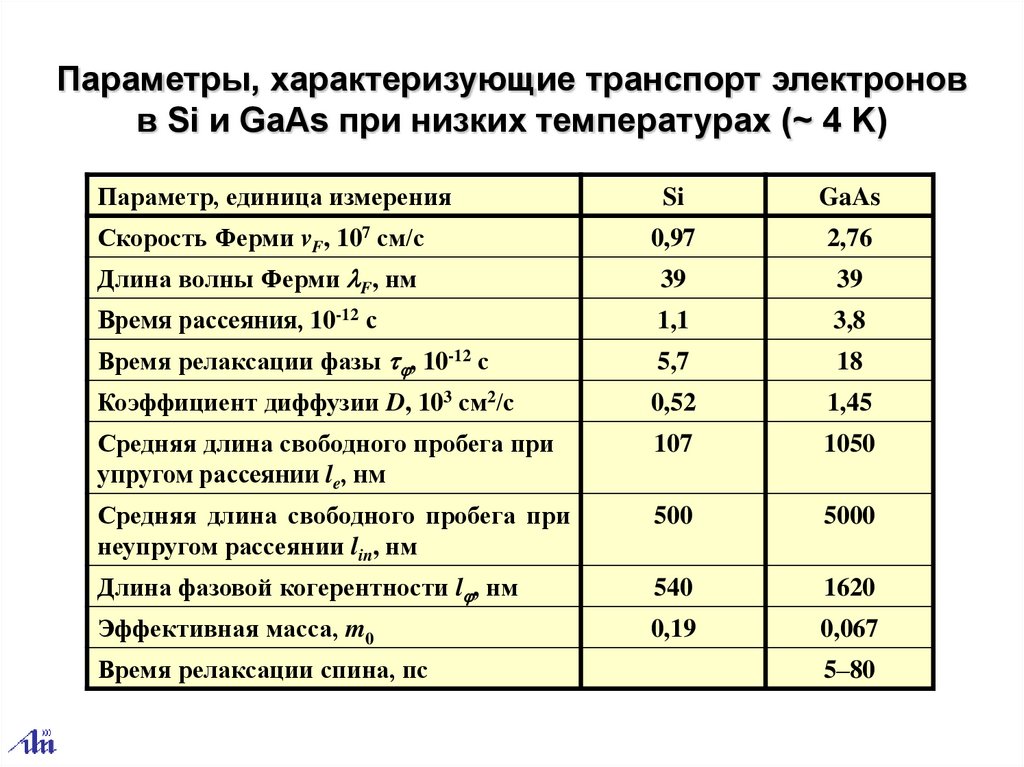
Параметры, характеризующие транспорт электроновв Si и GaAs при низких температурах (~ 4 K)
Параметр, единица измерения
Si
GaAs
Скорость Ферми vF, 107 см/с
0,97
2,76
Длина волны Ферми F, нм
39
39
Время рассеяния, 10-12 с
1,1
3,8
Время релаксации фазы , 10-12 с
5,7
18
Коэффициент диффузии D, 103 см2/с
0,52
1,45
Средняя длина свободного пробега при
упругом рассеянии le, нм
107
1050
Средняя длина свободного пробега при
неупругом рассеянии lin, нм
500
5000
Длина фазовой когерентности l , нм
540
1620
Эффективная масса, m0
0,19
0,067
Время релаксации спина, пс
5–80
15.
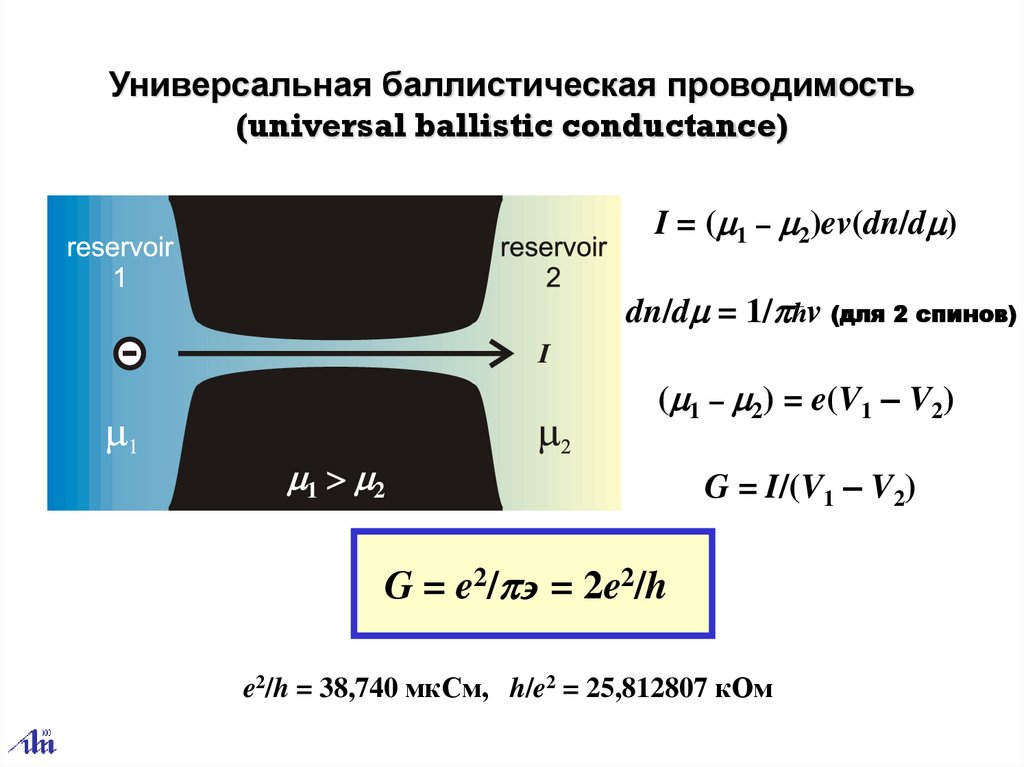
Универсальная баллистическая проводимость(universal ballistic conductance)
I = ( 1 – 2)ev(dn/d )
dn/d = 1/ ħv (для 2 спинов)
( 1 – 2) = e(V1 – V2)
1 2
G = I/(V1 – V2)
G = e2/ = 2e2/h
e2/h = 38,740 мкСм, h/e2 = 25,812807 кОм
16.
Квантовый точечный контакт(quantum point contact)
Conductance (2e2/h)
Vg
current
AlGaAs
GaAs
2DEG
G = N(2e2/h)
10
8
6
4
2
0
-2.0
-1.8 -1.6 -1.4 -1.2
Gate voltage Vg (V)
17.
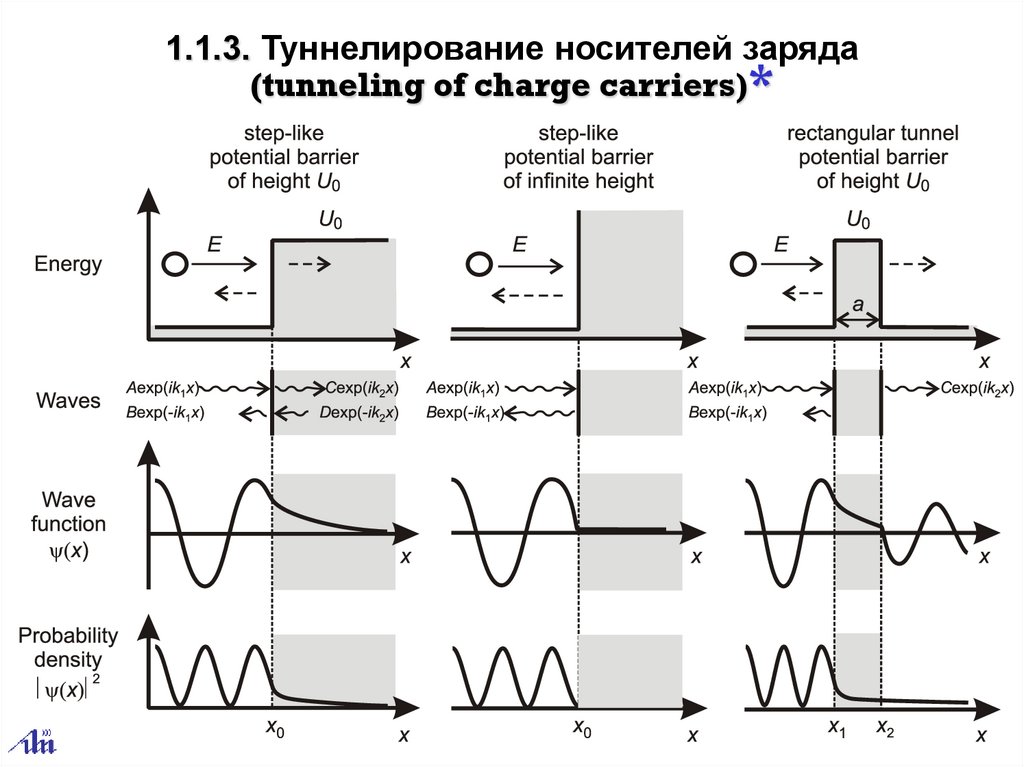
1.1.3. Туннелирование носителей заряда(tunneling of charge carriers)*
18.
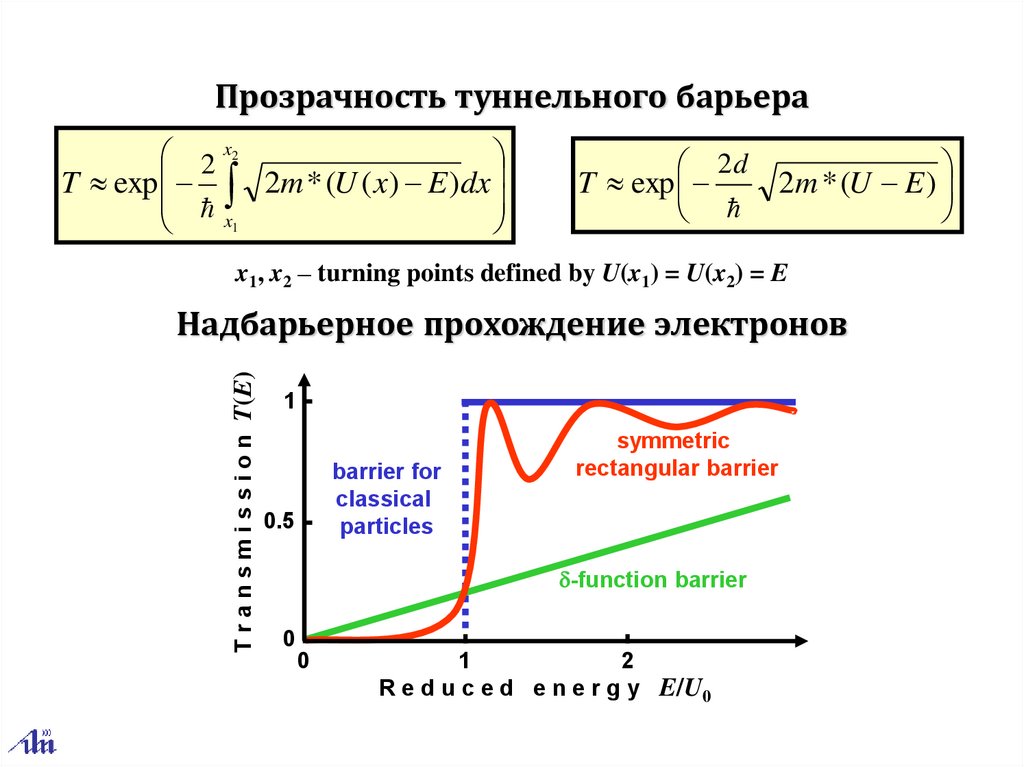
Прозрачность туннельного барьера2 x2
T exp 2m * (U ( x) E )dx
x
1
2d
T exp
2m * (U E )
x1, x2 – turning points defined by U(x1) = U(x2) = E
T r a n s m i s s i o n T(E)
Надбарьерное прохождение электронов
1
barrier for
classical
particles
0.5
symmetric
rectangular barrier
-function barrier
0
0
1
2
R e d u c e d e n e r g y E/U0
19.
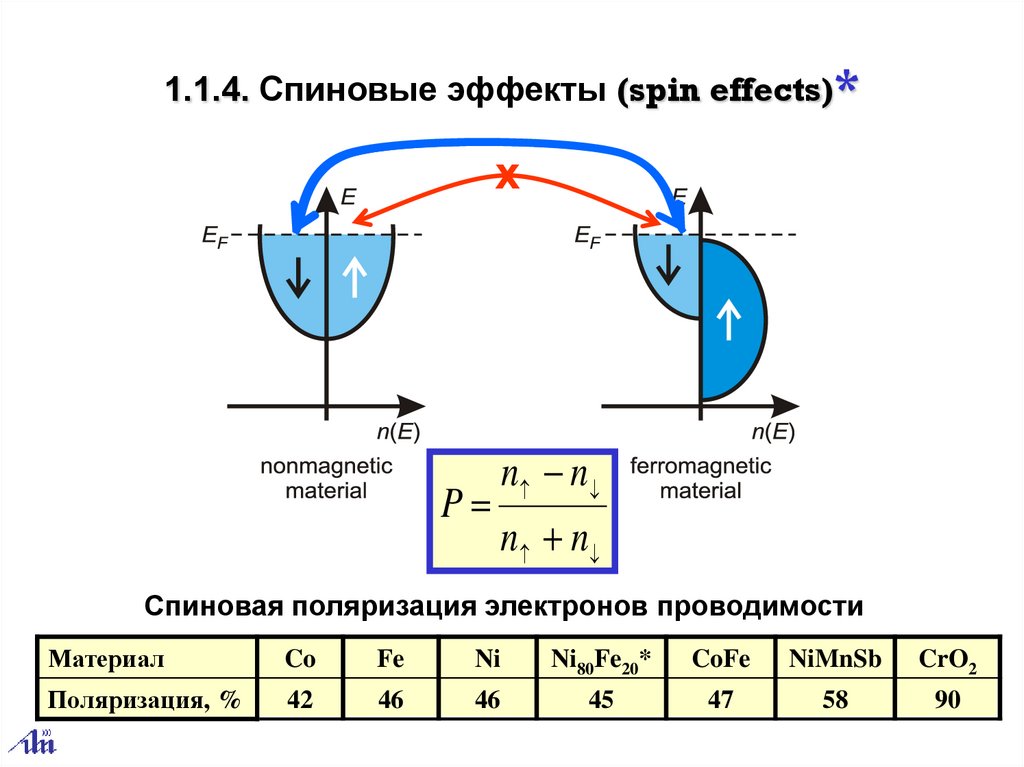
1.1.4. Спиновые эффекты (spin effects)*x
P
n n
n n
Спиновая поляризация электронов проводимости
Материал
Co
Fe
Ni
Ni80Fe20*
CoFe
NiMnSb
CrO2
Поляризация, %
42
46
46
45
47
58
90
20.
Фундаментальные явленияquantum
confinement
nanoelectronics
ballistic
transport
spin effects
tunneling
21.
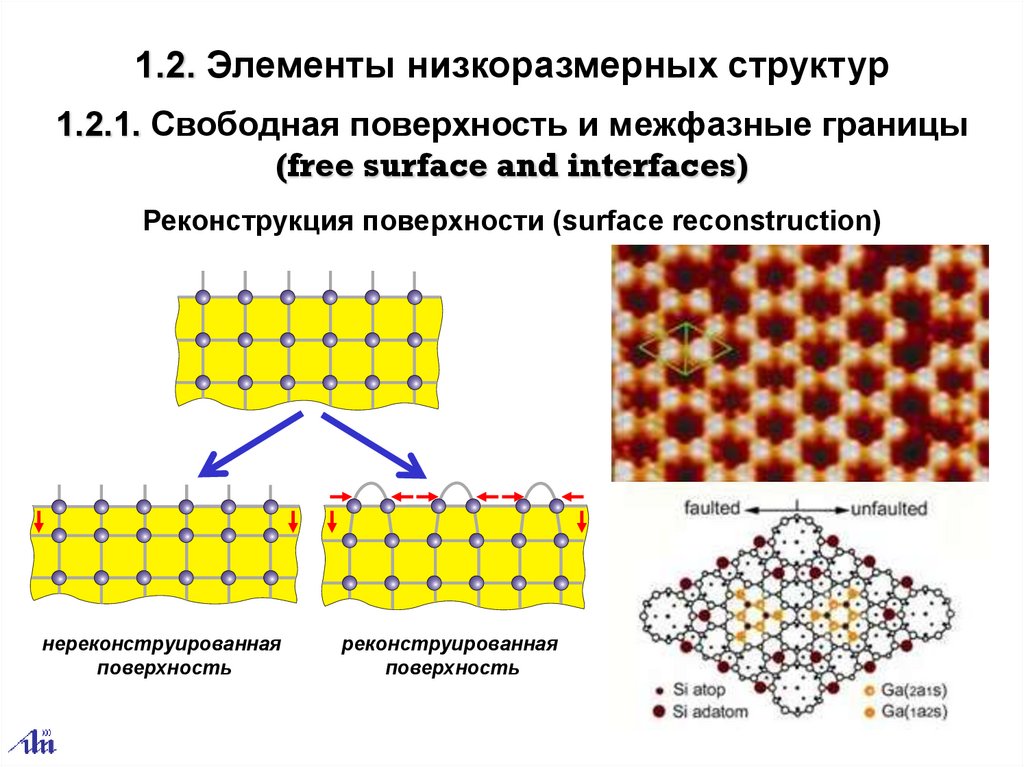
1.2. Элементы низкоразмерных структур1.2.1. Свободная поверхность и межфазные границы
(free surface and interfaces)
Реконструкция поверхности (surface reconstruction)
нереконструированная
поверхность
реконструированная
поверхность
22.
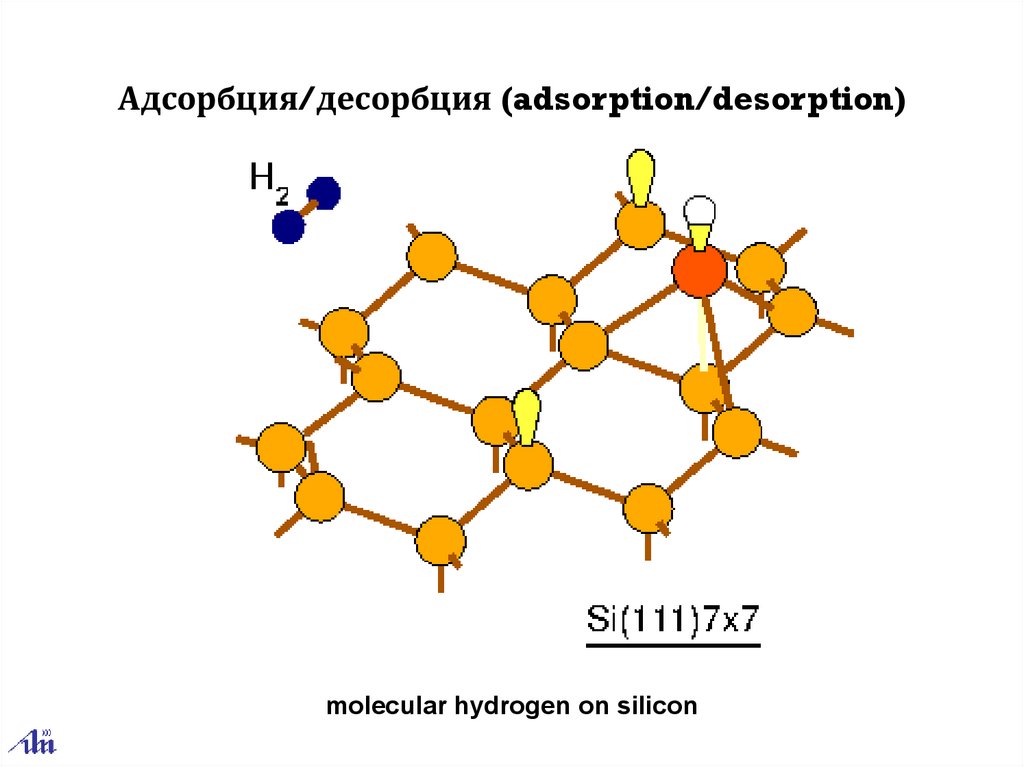
Адсорбция/десорбция (adsorption/desorption)molecular hydrogen on silicon
23.
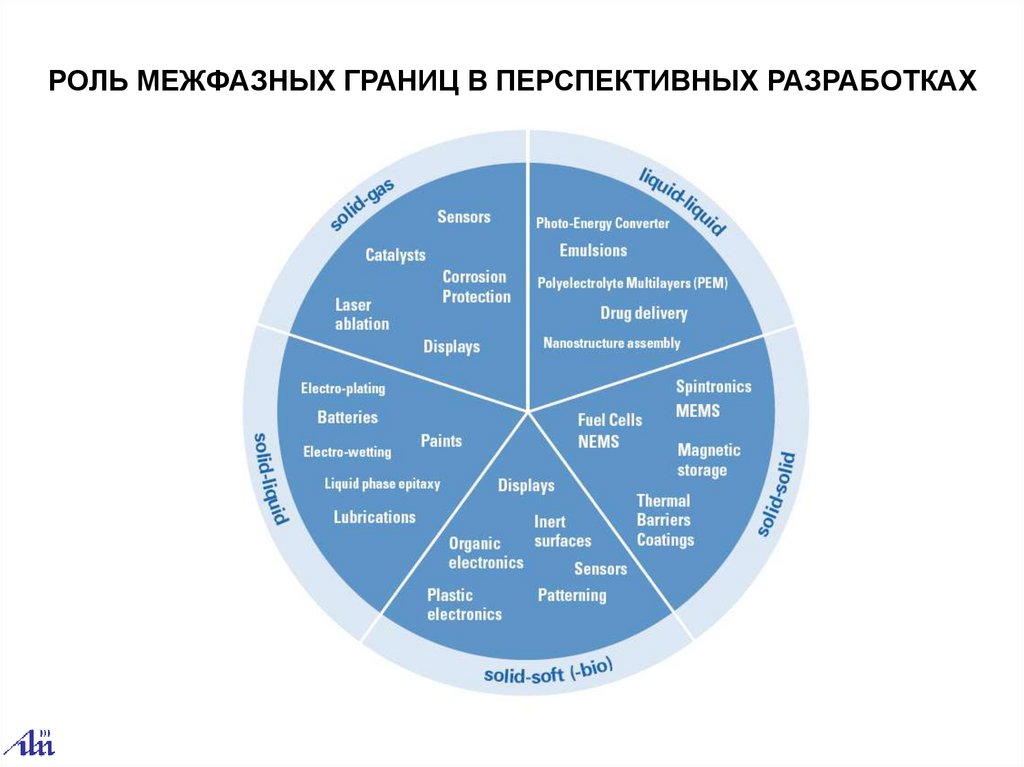
РОЛЬ МЕЖФАЗНЫХ ГРАНИЦ В ПЕРСПЕКТИВНЫХ РАЗРАБОТКАХ24.
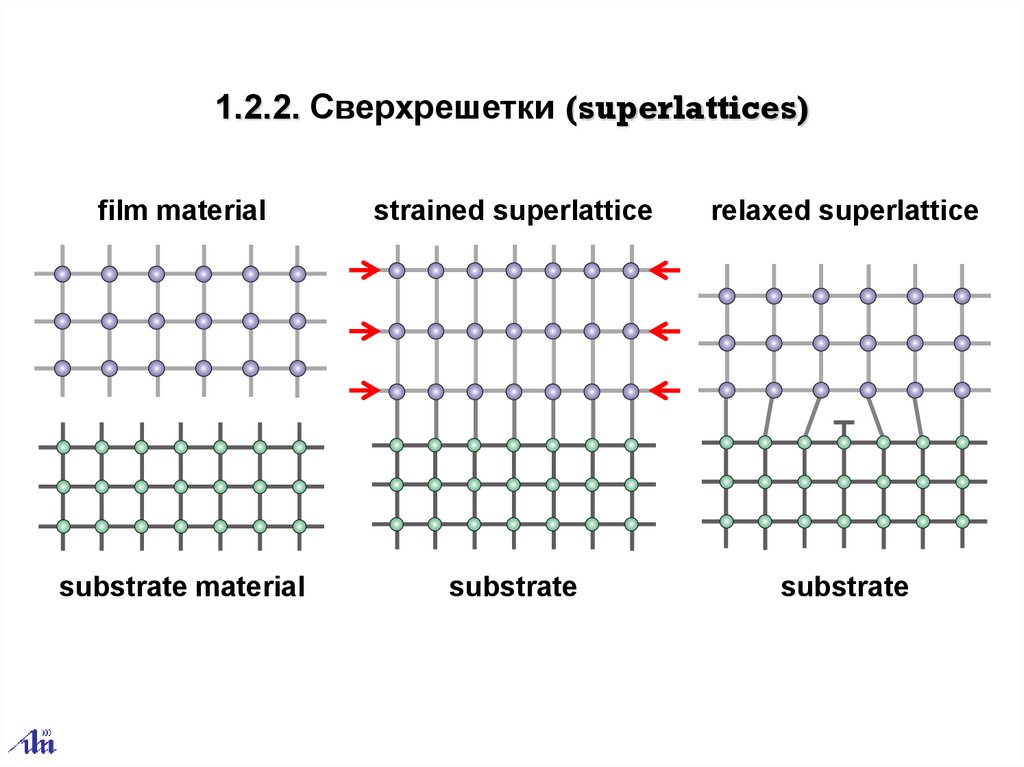
1.2.2. Сверхрешетки (superlattices)film material
strained superlattice
relaxed superlattice
substrate material
substrate
substrate
25.
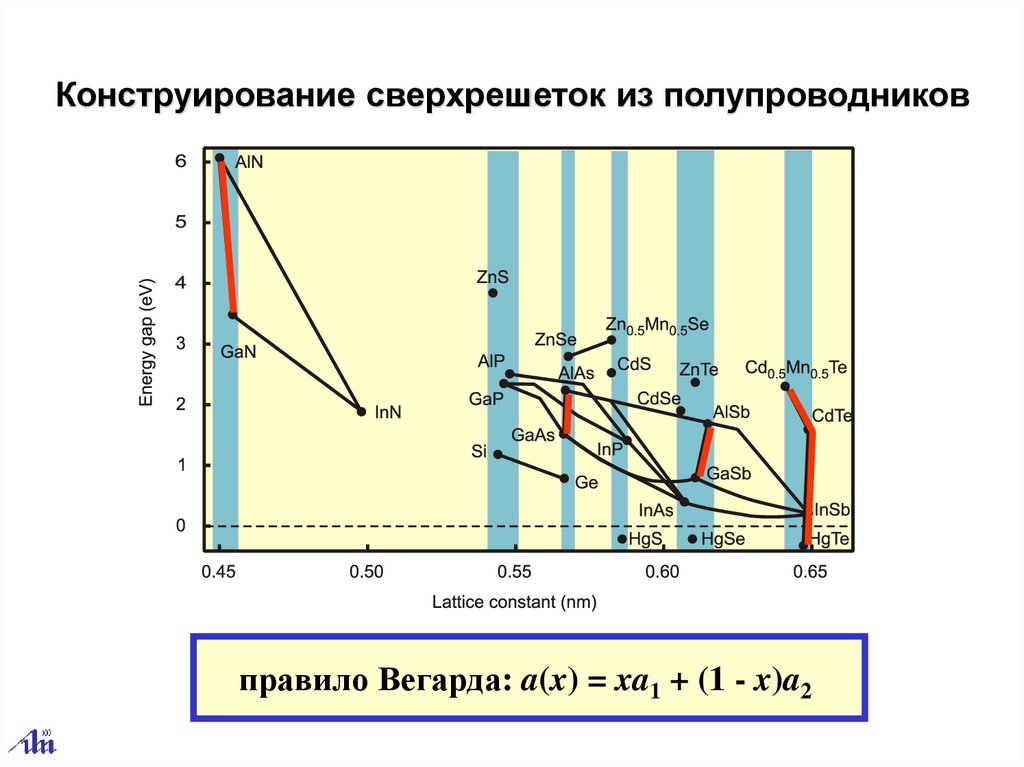
Конструирование сверхрешеток из полупроводниковправило Вегарда: a(x) = xa1 + (1 - x)a2
26.
Псевдоморфные сверхрешетки(pseudomorphic superlattices)
AlAs
GaAs
AlAs
GaAs
AlAs
GaAs
4 nm
5 nm
27.
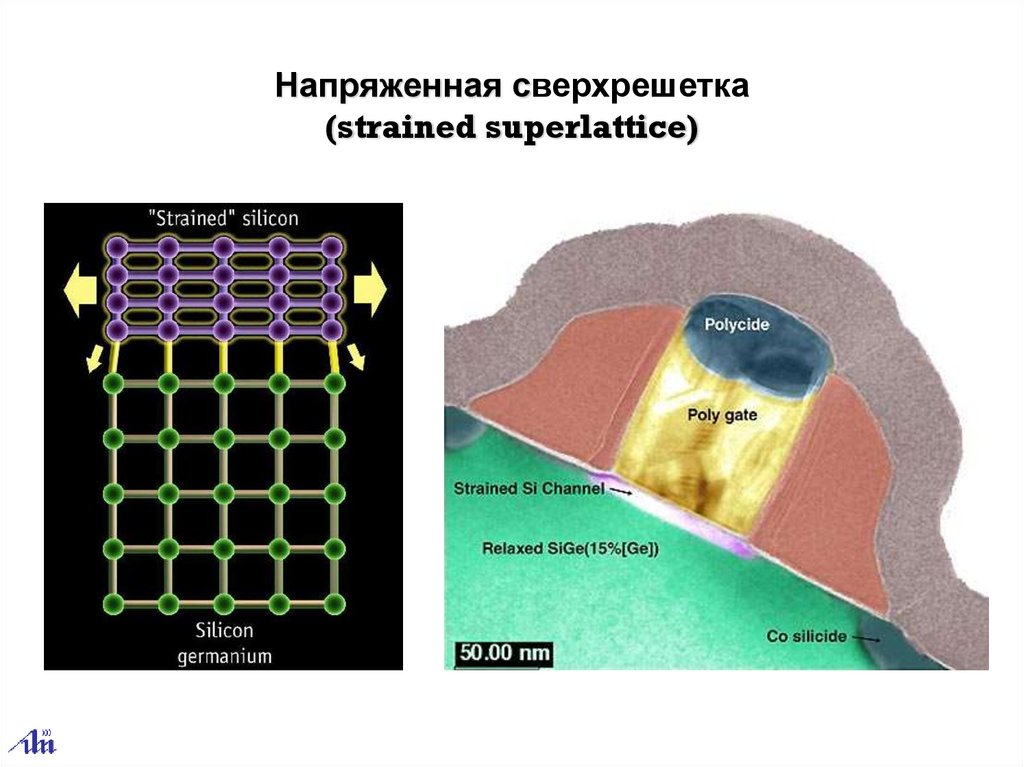
Напряженная сверхрешетка(strained superlattice)
28.
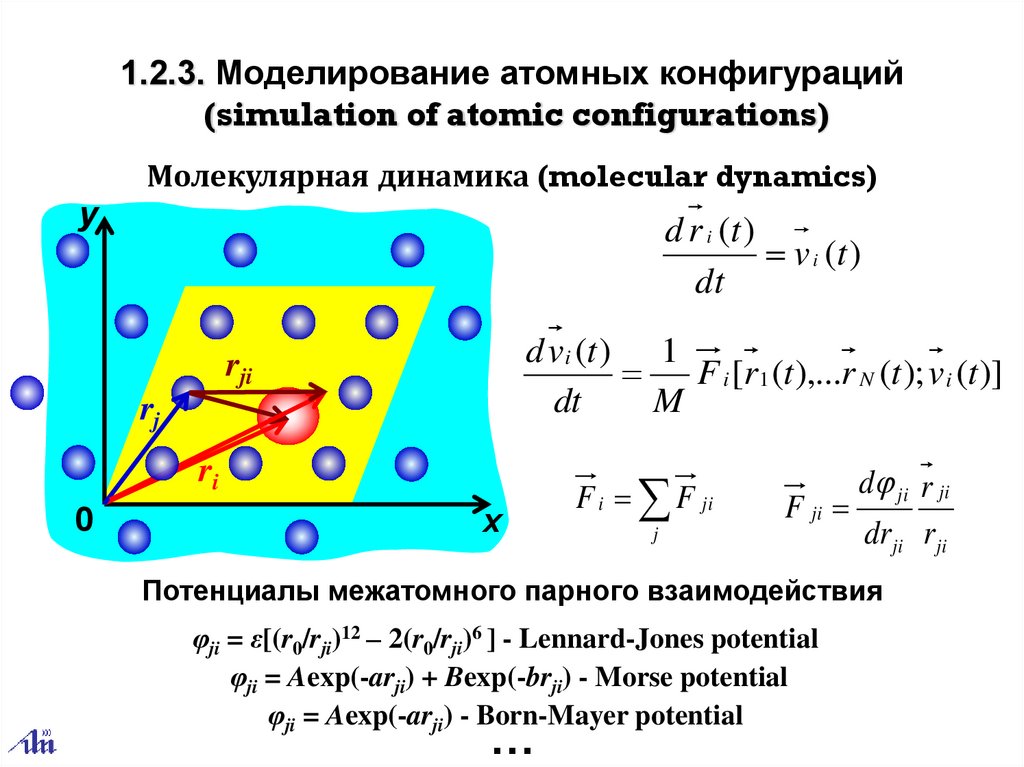
1.2.3. Моделирование атомных конфигураций(simulation of atomic configurations)
Молекулярная динамика (molecular dynamics)
y
d r i (t )
v i (t )
dt
d v i (t ) 1
F i [r1 (t ),...r N (t ); v i (t )]
dt
M
rji
rj
ri
0
x
F i F ji
F ji
j
d ji r ji
drji rji
Потенциалы межатомного парного взаимодействия
φji = ε[(r0/rji)12 – 2(r0/rji)6 ] - Lennard-Jones potential
φji = Aexp(-arji) + Bexp(-brji) - Morse potential
φji = Aexp(-arji) - Born-Mayer potential
…
29.
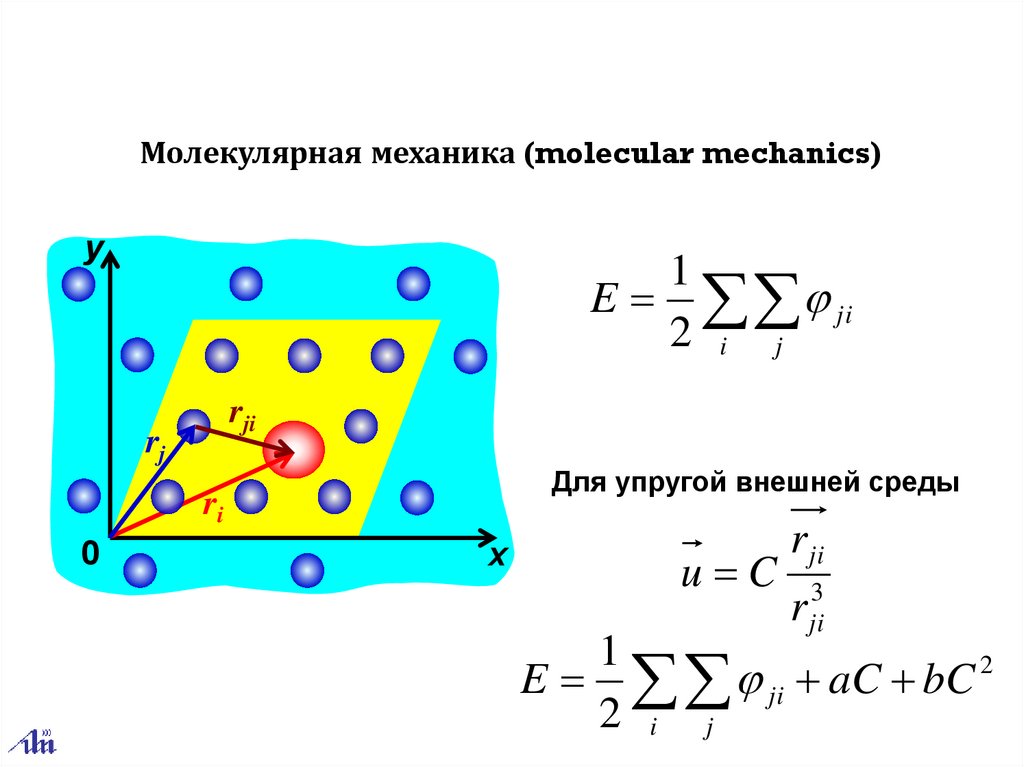
Молекулярная механика (molecular mechanics)y
1
E ji
2 i j
rji
rj
Для упругой внешней среды
ri
0
x
u C
r ji
r ji3
1
E ji aC bC 2
2 i j
30.
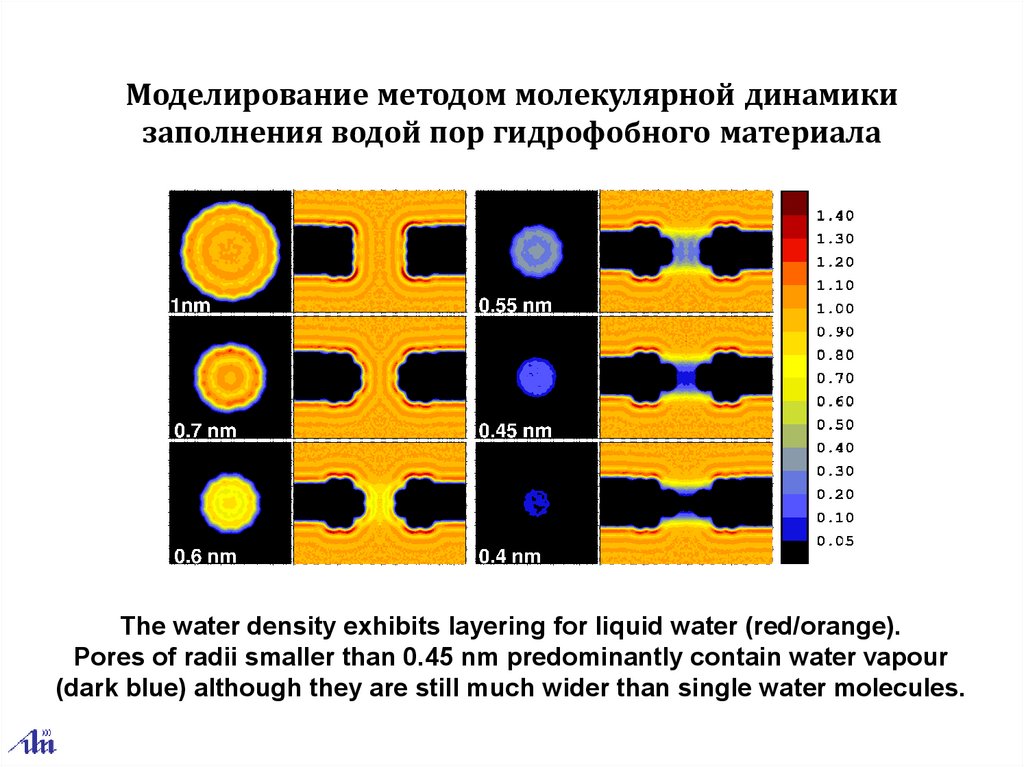
Моделирование методом молекулярной динамикизаполнения водой пор гидрофобного материала
The water density exhibits layering for liquid water (red/orange).
Pores of radii smaller than 0.45 nm predominantly contain water vapour
(dark blue) although they are still much wider than single water molecules.
31.
1.3. Структуры с квантовым ограничениемвнутренним электрическим полем
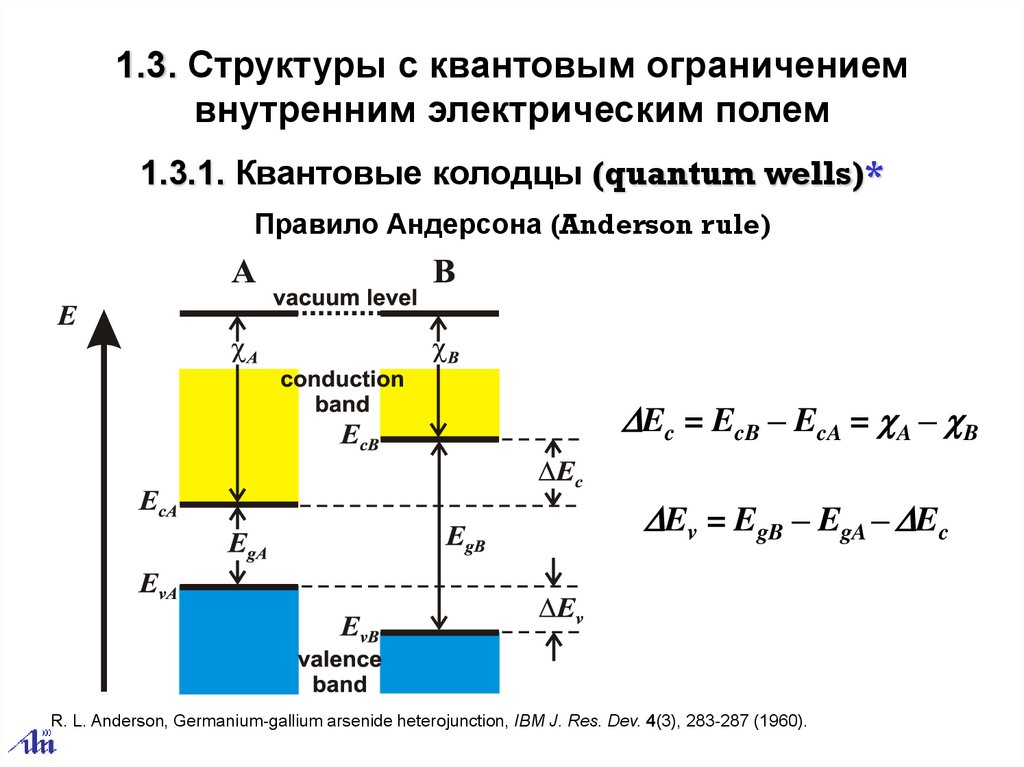
1.3.1. Квантовые колодцы (quantum wells)*
Правило Андерсона (Anderson rule)
DEc = EcB – EcA = cA – cB
DEv = EgB – EgA – DEc
R. L. Anderson, Germanium-gallium arsenide heterojunction, IBM J. Res. Dev. 4(3), 283-287 (1960).
32.
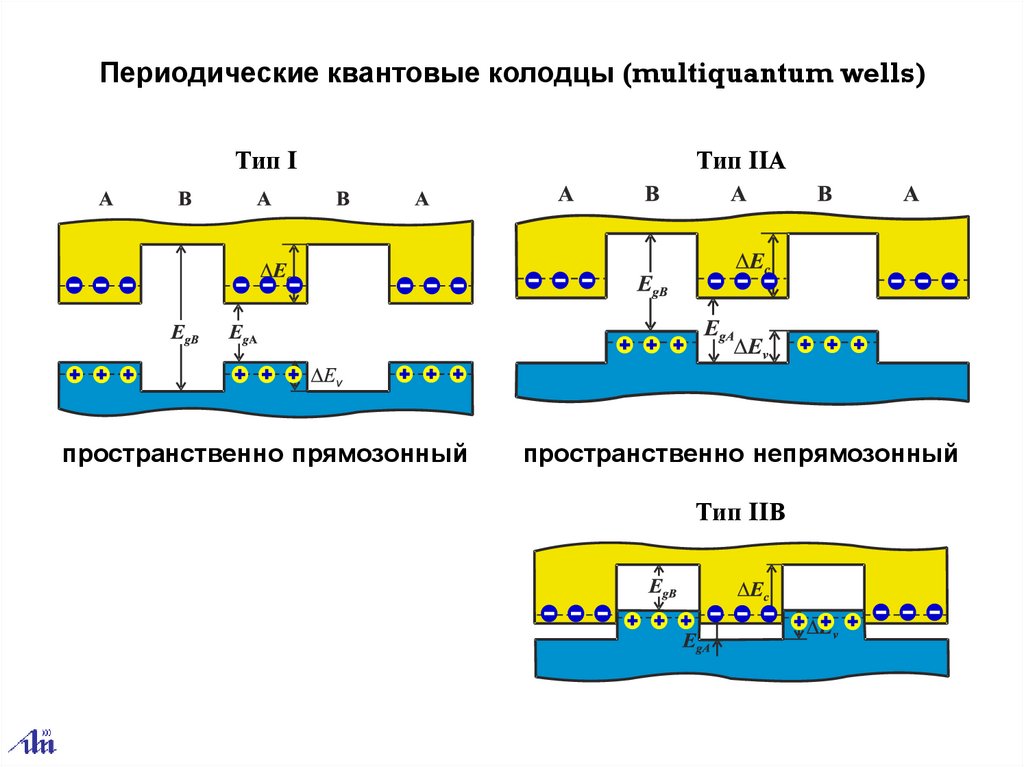
Периодические квантовые колодцы (multiquantum wells)Тип I
Тип IIА
пространственно прямозонный
пространственно непрямозонный
Тип IIВ
33.
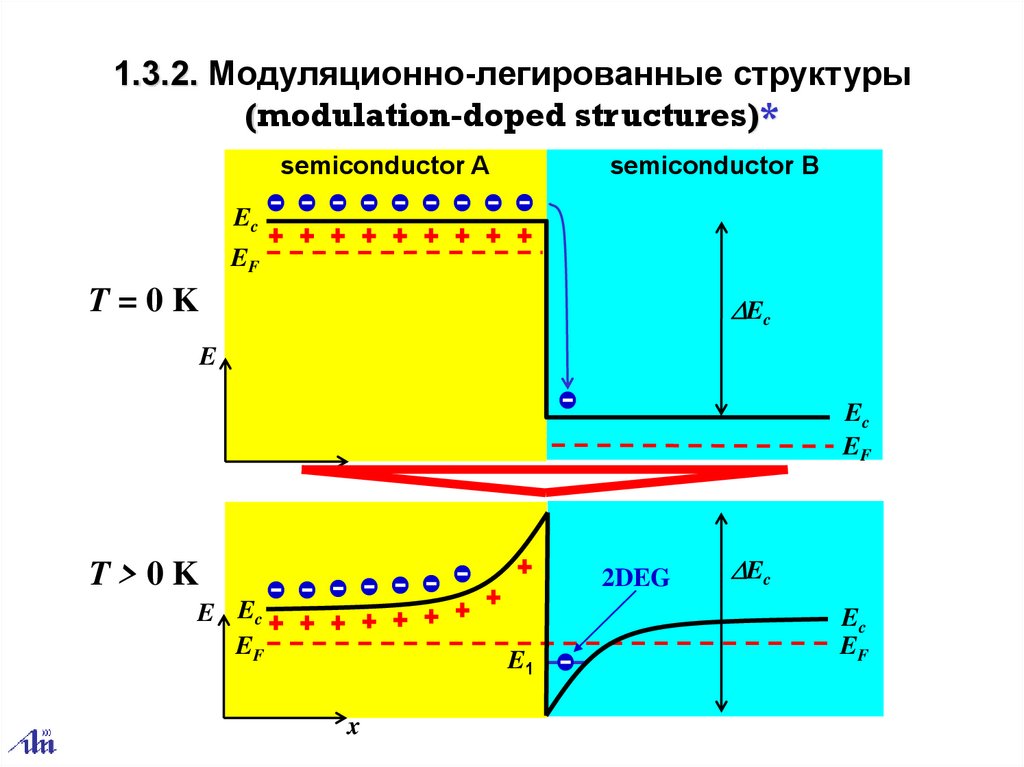
1.3.2. Модуляционно-легированные структуры(modulation-doped structures)*
semiconductor A
semiconductor B
Ec
EF
T=0K
DEc
E
Ec
EF
x
T>0K
2DEG
E Ec
EF
E1
x
DEc
Ec
EF
34.
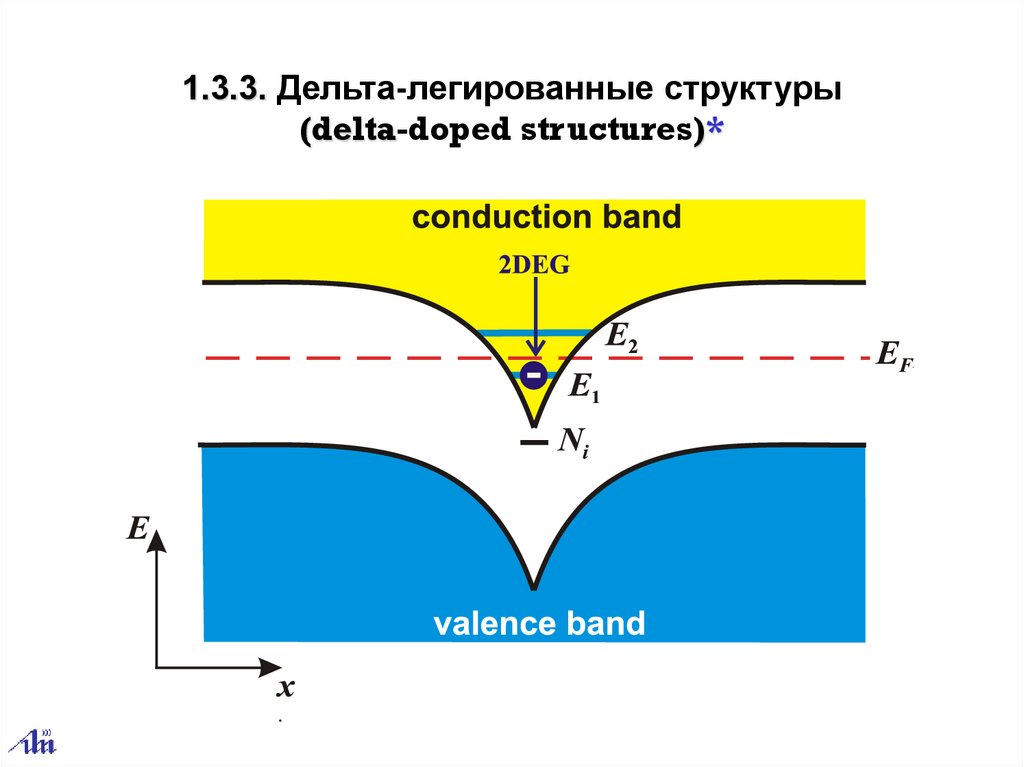
1.3.3. Дельта-легированные структуры(delta-doped structures)*
35.
1.4. Структуры с квантовым ограничениемвнешним электрическим полем
1.4.1. Структуры металл/диэлектрик/полупроводник
(metal/insulator/semiconductor structures)*
36.
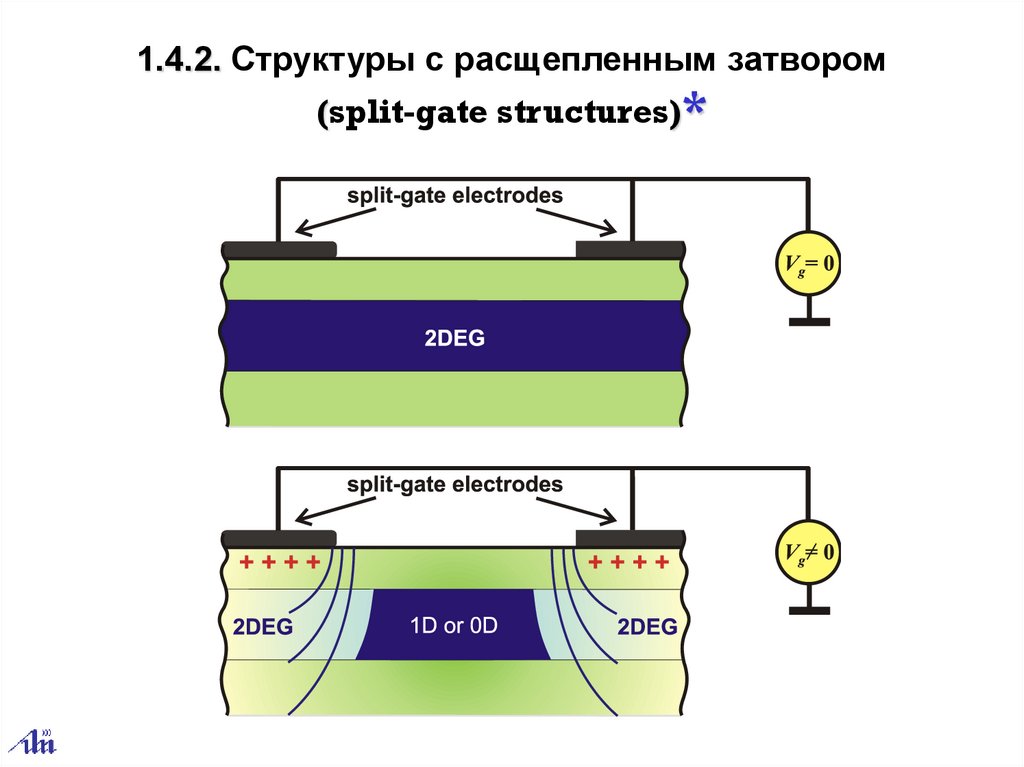
1.4.2. Структуры с расщепленным затвором(split-gate structures)*
37.
Квантовые точки в структурах с расщепленным затвором(split-gate defined quantum dots)












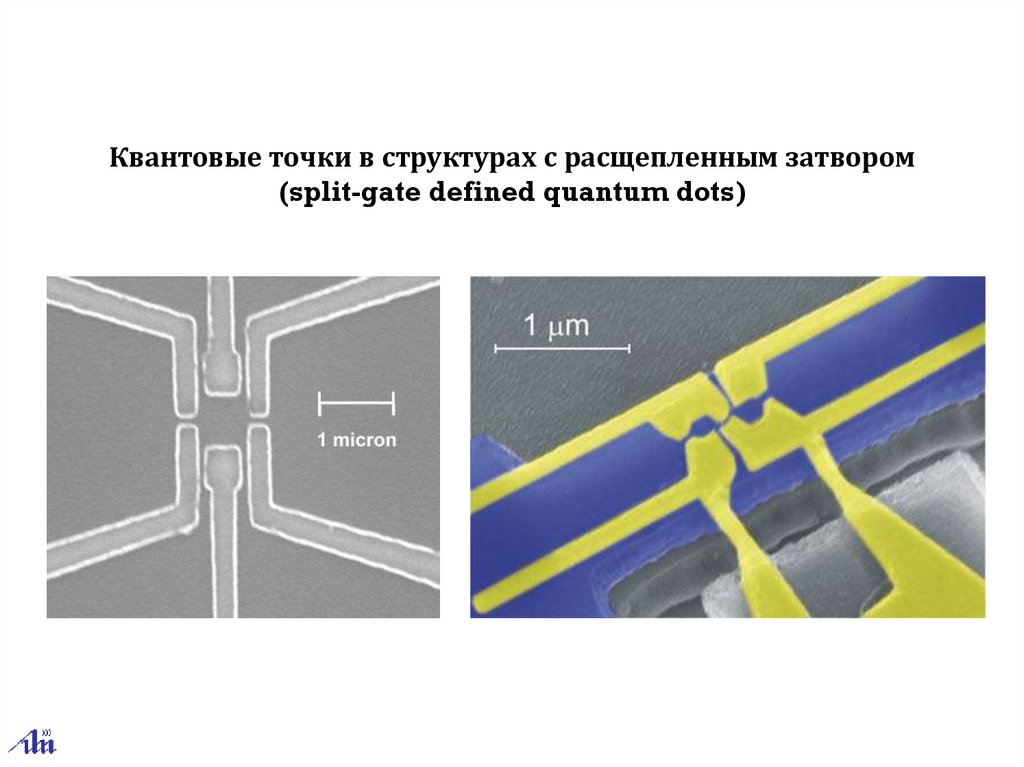
 Физика
Физика








