Похожие презентации:
Квазиравновесный конденсат поляритонов в GaAs микрорезонаторах в магнитном поле
1. Квазиравновесный конденсат поляритонов в GaAs микрорезонаторах в магнитном поле А.В. Черненко ИФТТ РАН
Квазиравновесный конденсат поляритонов в GaAsмикрорезонаторах в магнитном поле
А.В. Черненко
ИФТТ РАН
2. План доклада
• Ключевые понятия, используемых в докладе(микрорезонаторы, поляритоны, бозе-конденсат, и проч.)
• Конденсат поляритонов в планарном микрорезонаторе в
магнитном поле
• Конденсат поляритонов в микростолбиках в магнитном поле
• Резюме
3. Об основных терминах, используемых в докладе
Бозе-конденсат (Бозе-эйнштейновский конденсат)- макроскопическизаполненное когерентное основное состояние системы бозонов.
Существование конденсата (в 3D) случае-фундаментальное
термодинамическое свойство бозе-газа (Бозе, Эйнштейн 1924-1925,
Боголюбов 1947 г)
Квазиравновесный конденсат- конденсат в системе, которая отклоняется
от термодинамического равновесия, но «не сильно» (пояснения ниже).
Поляритоны(светоэкситоны)-квазичастицы, являющиеся комбинацией
кванта света и экситона( коррелированной электронно-дырочной пары)
Полупроводниковые микрорезонаторы (см следующий слайд)
4. Полупроводниковый микрорезонатор
Верхнеебрэгговское
зеркало
Нижнее
брэгговское
зеркало
Микро
резонатор
/2
Электронная микрография МР
Квантовые ямы
чередующиеся /4 слои(AlAs/AlGaAs)
Распределение плотности поля |E|2 в образце
5. Полупроводниковый микрорезонатор (microcavity)-прямое развитие технологии лазерных структур
Полупроводниковый микрорезонатор (microcavity)прямое развитие технологии лазерных структурПоверхностно-излучающий лазер с вертикальным резонатором (Vertically surface
emitting laser) VCSEL
SEM изображение
6. Молекулярно-пучковая эпитаксия
МПЭ обеспечивает наивысшее качество интерфейса, характеристикой которогоявляется ширина линий фотолюминесценции (и/или высокая подвижность носителей)
7. Квантовомеханическая задача: частица в потенциальной яме
Квантовая яма типа I
8. Электроны и дырки в GaAs
Зонная структура GaAs9. Экситоны в полупроводниках(1)
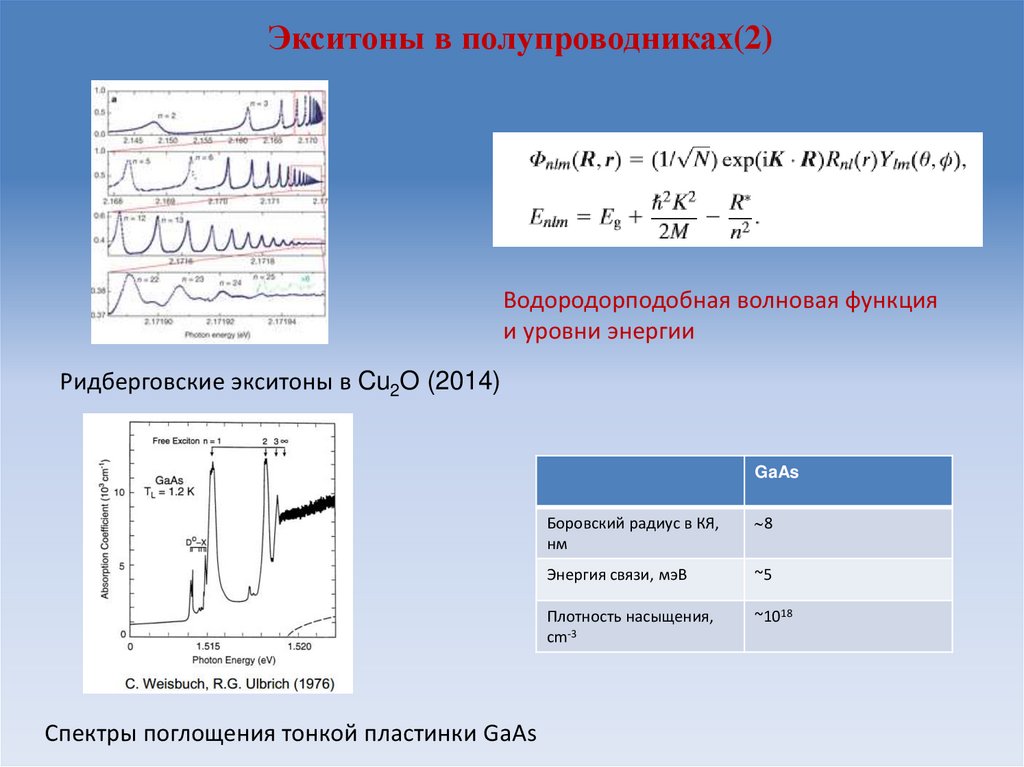
Экситон (Ванье-Мотта) во многих случаях ведёт себя как аналог атома водорода10. Экситоны в полупроводниках(2)
Водородорподобная волновая функцияи уровни энергии
Ридберговские экситоны в Cu2O (2014)
GaAs
Спектры поглощения тонкой пластинки GaAs
Боровский радиус в КЯ,
нм
8
Энергия связи, мэВ
~5
Плотность насыщения,
cm-3
~1018
11.
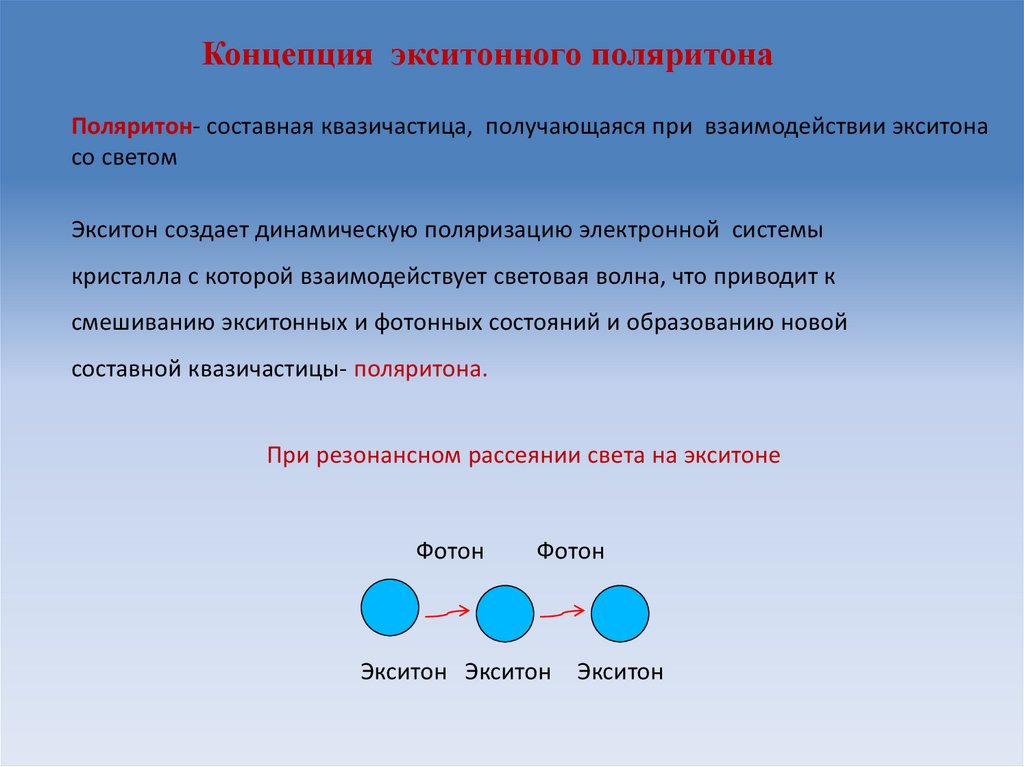
Концепция экситонного поляритонаПоляритон- составная квазичастица, получающаяся при взаимодействии экситона
со светом
Экситон создает динамическую поляризацию электронной системы
кристалла с которой взаимодействует световая волна, что приводит к
смешиванию экситонных и фотонных состояний и образованию новой
составной квазичастицы- поляритона.
При резонансном рассеянии света на экситоне
Фотон
Фотон
Экситон Экситон Экситон
12.
Поляритон в микрорезонаторе13. Поляритон-составная квазичастица
Гамильтониан экситон-фотонной системыЭнергия
ВП ветвь
W0
НП ветвь
0 q
Коэффициенты Хопфилда
где
14.
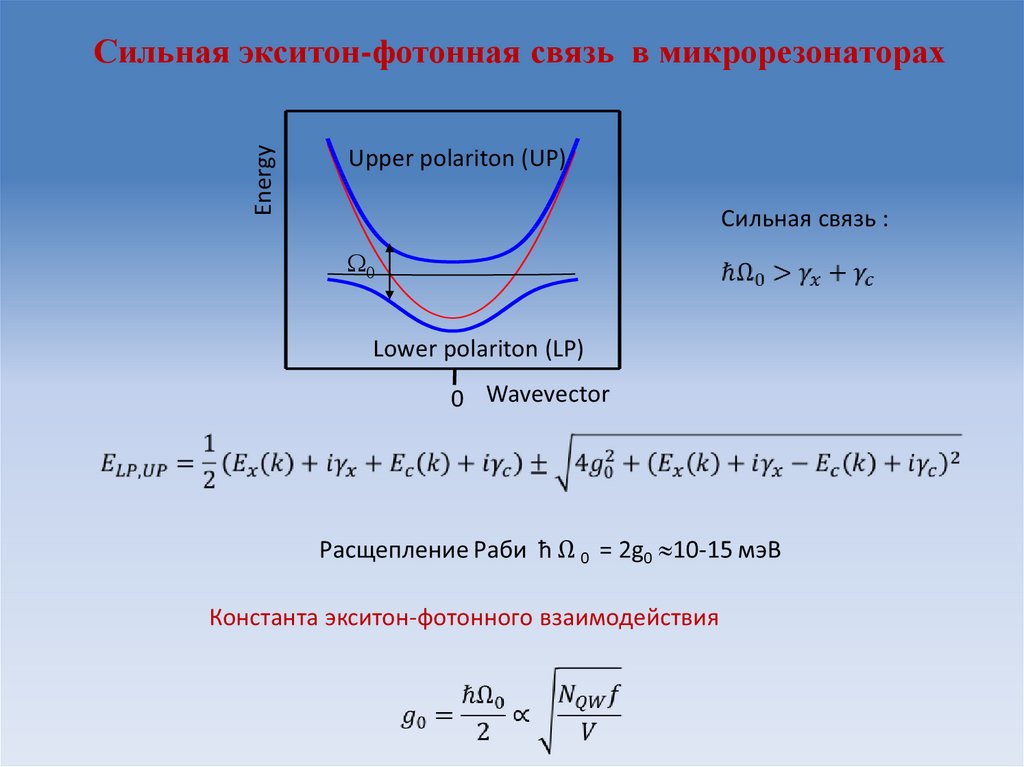
EnergyСильная экситон-фотонная связь в микрорезонаторах
Upper polariton (UP)
Сильная связь :
W0
Lower polariton (LP)
0 Wavevector
Константа экситон-фотонного взаимодействия
15.
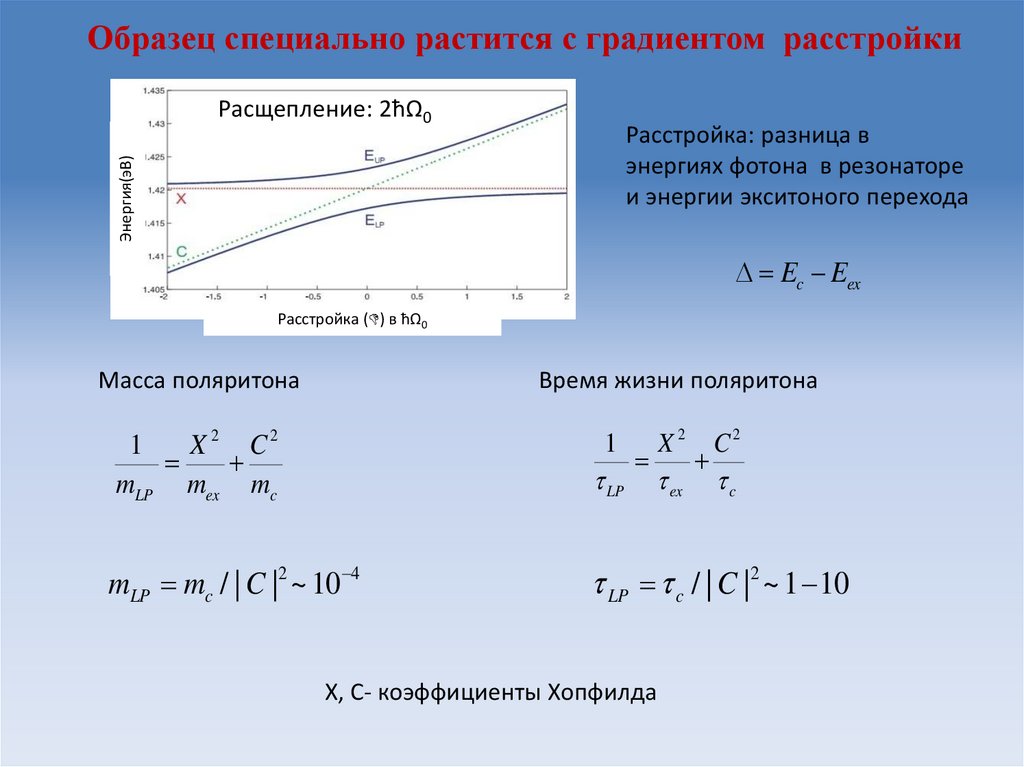
Образец специально растится с градиентом расстройкиРасщепление: 2ħΩ0
Энергия(эВ)
Расстройка: разница в
энергиях фотона в резонаторе
и энергии экситоного перехода
Ec Eex
Расстройка ( ) в ħΩ0
Масса поляритона
Время жизни поляритона
X 2 C2
ex c
1
X 2 C2
mLP mex mc
LP
mLP mc / | C |2 ~ 10 4
LP c / | C |2 ~ 1 10
1
X, C- коэффициенты Хопфилда
16.
Бозе-конденсат 2D поляритонов?Таблица характерных параметров газа атомов, экситонов и поляритонов
Поляритонная система в микрорезонаторе- открытая диссипативная система, далёкая
от равновесия, времена энергетической и спиновой релаксаций в которой сравнимы
со временем жизни поляритонов
Y. Yamomoto, A. Imamoglu, IEEE 1996
17. Бозе-конденсация и бозе-конденсат
• Бозе-конденсат-это когерентное, макроскопически заполненноеосновное состояние системы бозонов.
• Бозе-конденсация –фазовый термодинамический переход,
сопровождающийся спонтанным установлением когерентности в
системе (образованием бозе-конденсата).
• Бозе-конденсация частиц, ограниченных в пространстве возможна
как в 3D так и 2D случаях. В 2D случае (квантовый ящик размером
LxL )и дискретного энергетического спектра i
1
nc
L
ln
2
T T
2
T
2
mk B T
Бозе-конденсация идеального невзаимодействующего Бозе-газа
невозможна.
18.
Угловое распределение ФЛ микрорезонатораДля фотона в МР можно определить массу
19. Измерения ФЛ поляритонов в реальном и к-пространствах
ВВ
1,0
0,8
Возбуждение непрерывным линейно
поляризованным Ti:Sp лазером в
первый минимум отражения Брэгговских
зеркал.
R
0,6
0,4
0,2
0,0
740
760
780
800
Wavelength, nm
820
840
Размер пятна возбуждения d= 40 мкм
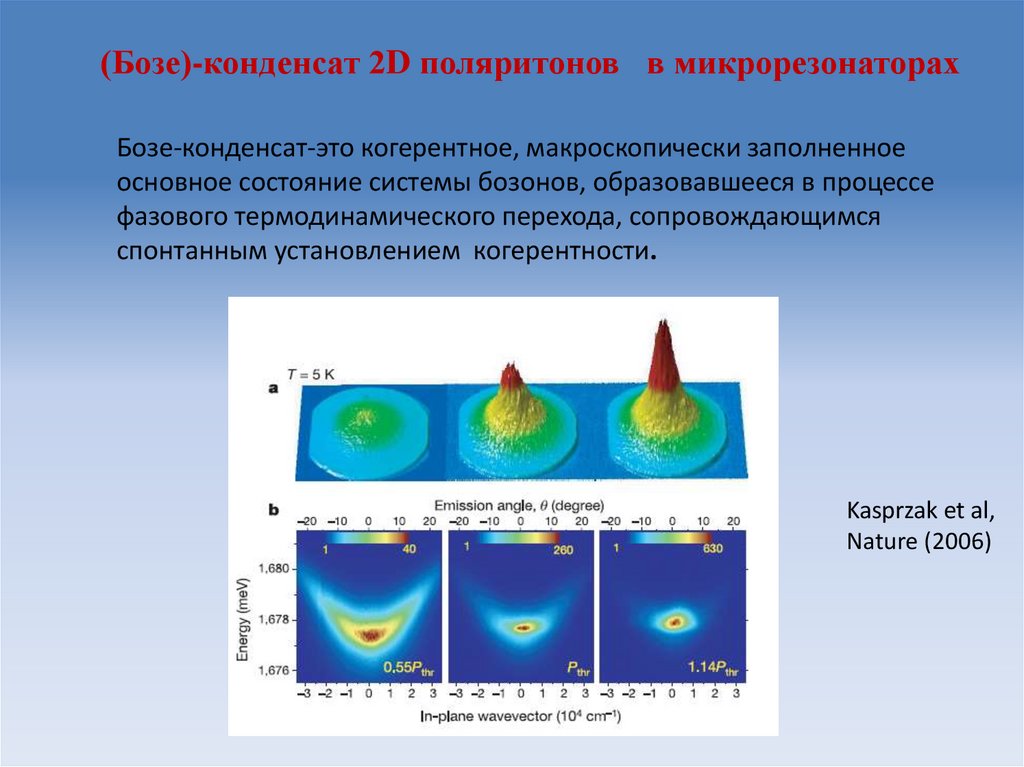
20. (Бозе)-конденсат 2D поляритонов в микрорезонаторах
Бозе-конденсат-это когерентное, макроскопически заполненноеосновное состояние системы бозонов, образовавшееся в процессе
фазового термодинамического перехода, сопровождающимся
спонтанным установлением когерентности.
Kasprzak et al,
Nature (2006)
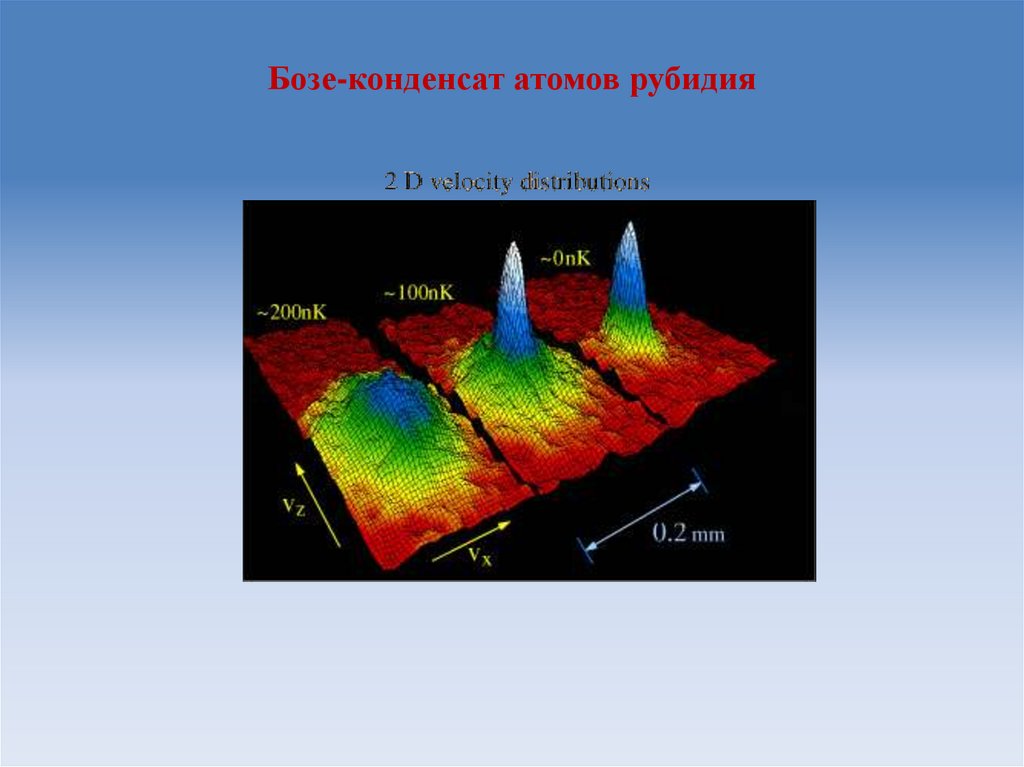
21. Бозе-конденсат атомов рубидия
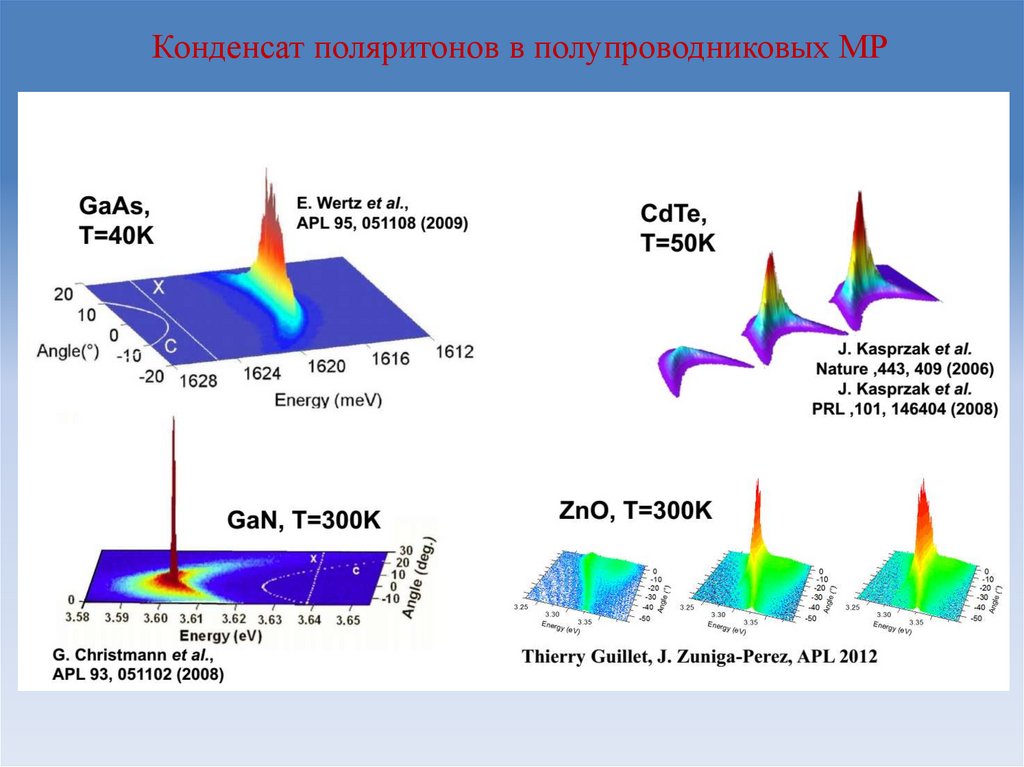
22.
Конденсат поляритонов в полупроводниковых МР23. Квазиравновесный конденсат
Распределение интенсивности излучения поляритонов по k|| приразных Tb. Для Tb=6 K, сплошная-Бозе с Т=6 K, пунктир-Больцман c
T=25 K
Также говорят о динамическом конденсате, неравновесном конденсате и о
«поляритонном лазере»
В.Д. Кулаковский и др. Письма в ЖЭТФ 2010
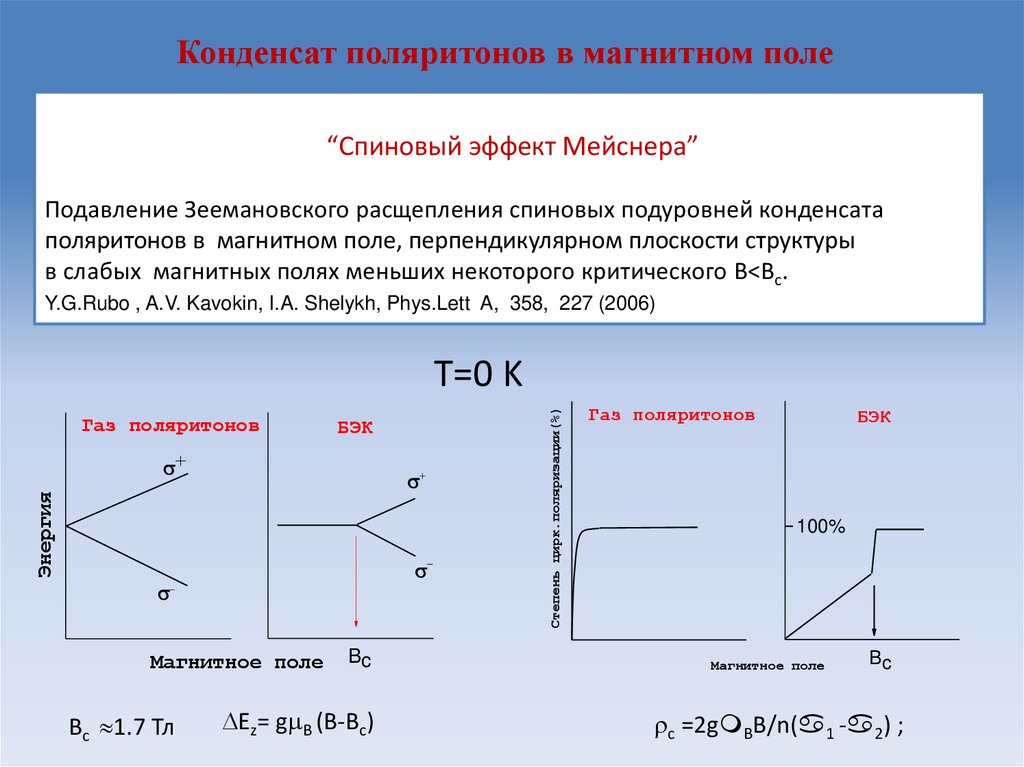
24. Конденсат поляритонов в магнитном поле
“Спиновый эффект Мейснера”Подавление Зеемановского расщепления спиновых подуровней конденсата
поляритонов в магнитном поле, перпендикулярном плоскости структуры
в слабых магнитных полях меньших некоторого критического B<Bc.
Y.G.Rubo , A.V. Kavokin, I.A. Shelykh, Phys.Lett A, 358, 227 (2006)
Газ поляритонов
БЭК
Энергия
Магнитное поле
Bc 1.7 Тл
Bc
Ez= g B (B-Bc)
Степень цирк.поляризации(%)
T=0 K
Газ поляритонов
БЭК
100%
Магнитное поле
Bc
c =2g BB/n( 1 - 2) ;
25. БЭК поляритонов в магнитном поле (теория)
Y.G.Rubo , A.V. Kavokin, I.A. Shelykh, Phys.Lett A, 358, 227 (2006)Свободная энергия БЭК в магнитном поле B
F n B gBS z
1
( 1 2 )n 2 2( 1 2 ) S z2
4
где 1 , 2 – константы поляритон-поляритонного взаимодействия
Для паралелльно и антипараллельно ориентированных спинов пары поляритонов.
n n1 n2
n – полное число поляритонов, n1 и n2
Sz n1 n2
Критическое магнитное поле
Bc
2n 1
g B
Микроскопически эффект можно объяснить тем, что Зеемановское расщепление
спиновых уровней конденсата в точности компенсируется фиолетовым сдвигом
уровней поляритонов из-за перераспределением поляритонов между уровнями
26. Конденсат поляритонов в магнитном поле (I) (эксперимент)
Газ поляритоновБЭК
Энергия
Магнитное поле
Степень цирк.поляризации(%)
А. V. Larionov et al. PRL 2010.
Газ поляритонов
Bc
Bc 1.7 Тл
БЭК
100%
Магнитное поле
Ez= g B (B-Bc)
Bc
27. Неравновесный конденсат поляритонов магнитном поле (теория)
Плотность (свободной) энергии конденсата в магнитном поле BF n n
1
( 1 2 )n 2 ( 1 2 ) S z2 B gBS z
4
где 1 , 2 – константы поляритон-поляритонного взаимодействия
Для паралелльно и антипараллельно ориентированных спинов пары поляритонов
α1 >α2 . n± -число поляритонов с проекциями спина вдоль и противоположно Oz
Минимизируем F (n, Sz) по n- и n+
Величина Зеемановского расщепления однозначно связана
со степенью циркулярной поляризации
EZee B g eff B ( 1 2 )n c
J.Fischer et al.
Phys.Rev.Lett 112, 093902(2014)
28. Если T>0
Если T>0E 2W S z
1
( 1 2 )n 2 ( 1 2 ) S z2
4
n/2
Sz
В пределе T 0
B<Bc:
c 2g BB/n( 1 - 2) ; Зееман 0
B>Bc: c 1 g B (B-Bc)
j n / 2
n/2
j n / 2
j exp( E j / k BT )
exp( E j / k BT )
При T>0 K полного
подавления зеемановского
расщепления не достигается,
а конденсат не является
100% поляризованным
Критическое поле Bc отсутствует
29. Образец
ВерхнееБрэгговское
зеркало
Микрорезонатор
/2
Нижнее
Брэгговское
зеркало
Квантовые ямы
чередующиеся /4 слои(AlAs/AlGaAs)
n pol nQW
X NQW
Добротность Q >10000
NQW=12 GaAs(13 nm)/AlAs(4 nm) QW
Расщепление Раби 2ħW0=10 мэВ
Диапазон расстроек =Ec-Ex =-9-+2 meV
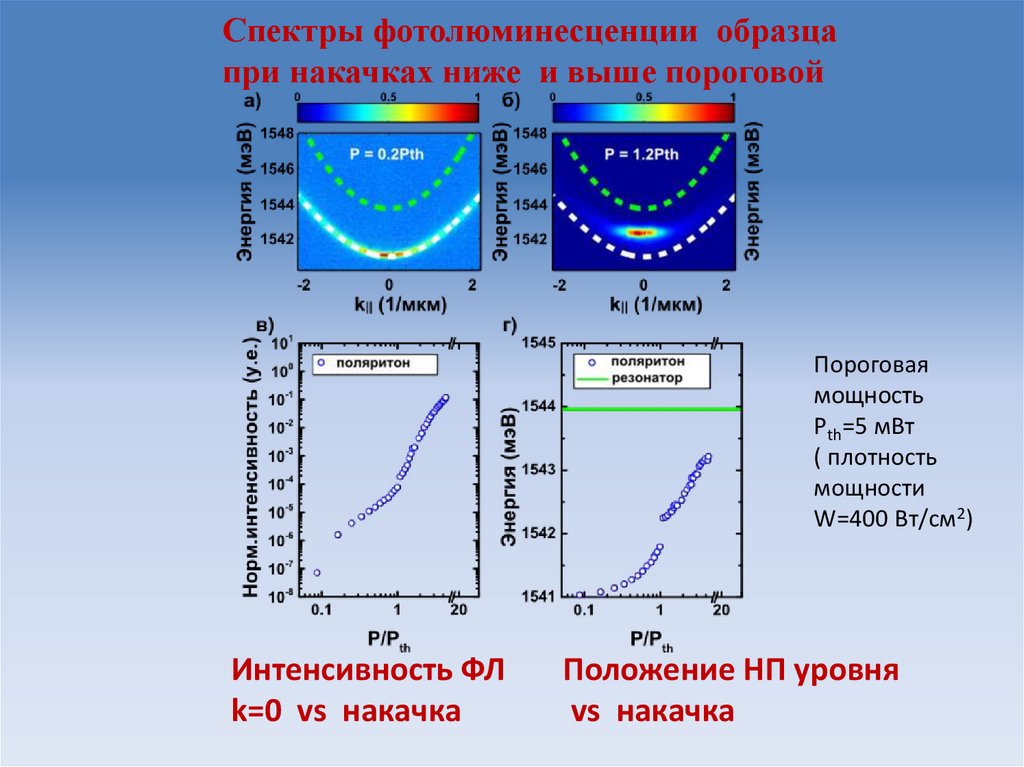
30.
Спектры фотолюминесценции образцапри накачках ниже и выше пороговой
Пороговая
мощность
Pth=5 мВт
( плотность
мощности
W=400 Вт/см2)
Интенсивность ФЛ
k=0 vs накачка
Положение НП уровня
vs накачка
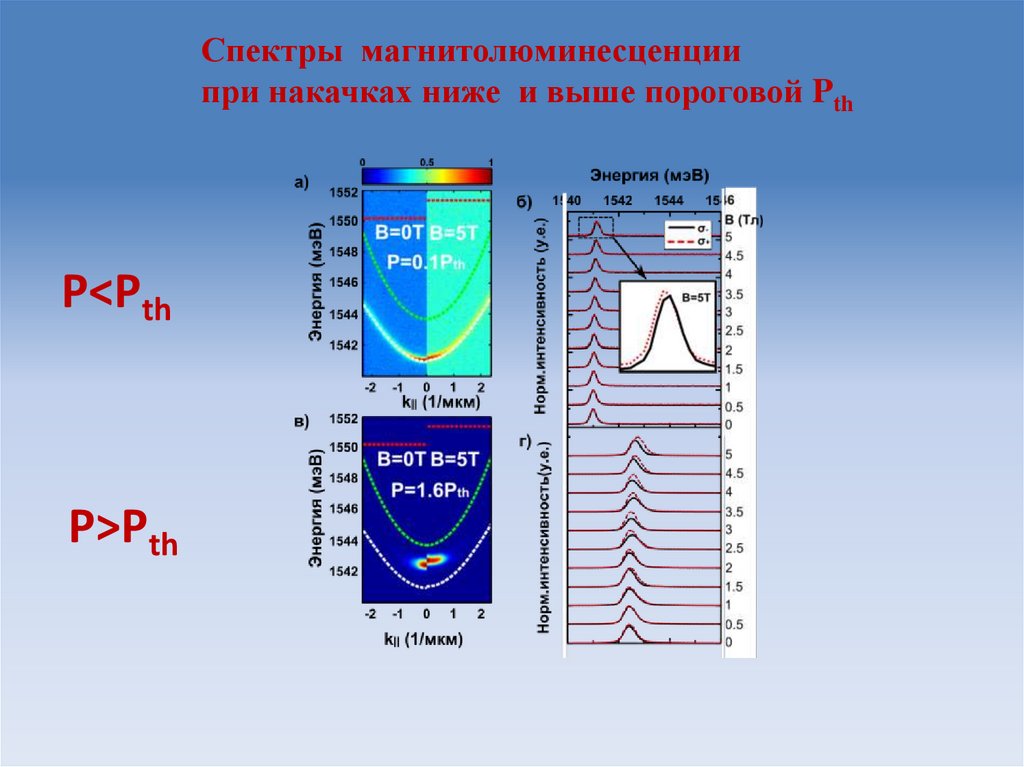
31.
Спектры магнитолюминесценциипри накачках ниже и выше пороговой Pth
P<Pth
P>Pth
32. Зеемановское расщепление и циркулярная поляризация конденсата(эксперимент)
расстройка δ(B=0)=-6.5 мэВ33.
Зеемановское расщепление и циркулярная поляризацияЗеемановское расщепление
Поляризация
«Неравновесный спиновый эффект Мейсснера» (А.Кавокин)
Нет полного подавления зеемановского расщепления, зато возможна
смена его знака .
34. Система поляритонов при значительных накачках (P>>Pth )
Система поляритонов при значительных накачках (P>>Pth )Импульсное нерезонансное
возбуждение Ti:Sp
лазером ( имп 50 пс)
Зеемановское расщепление и диамагнитный сдвиг отсутствуют
35. Спектры ФЛ при разных накачках
36. Диамагнитый сдвиг уровня конденсата поляритонов
(n) (0) /(1 n / 2nc )nc 2 / aB2 6.4 1011 см-2
aB 10 нм боровский радиус экситона
Диамагнитная константа
Edia ( B) B 2
1 ( G ( ) aB m 1 )2
100 / me
2
LP 6 мкэВ/T2
Cond 10 мкэВ/T2
G ( ) Коэффициент,
1 2 5.2 10 12
мэВсм2
зависящий от
ширины ямы
37. 2. Поляритоны в микростолбиках
D. Bajoni et al. PRL 20080.5 мм
38. Конденсат поляритонов в микростолбиках в магнитном поле
• Величина расщепление между спиновымиподуровнями конденсата поляритонов в магнитном поле
должна зависеть от накачки, но этого не наблюдалось
ранее
• Можно ли объяснить особенности в поведении
поляризации учётом взаимодействия конденсата
поляритонов с экситонным резервуаром? (Sturm et al.
PRB2015 )
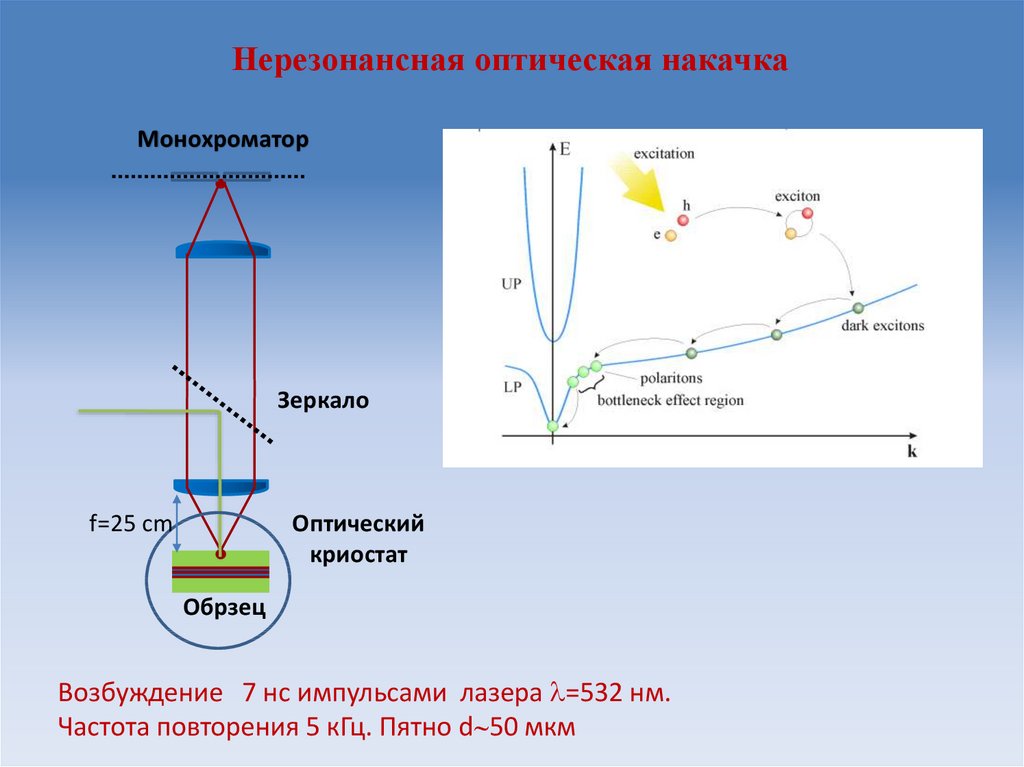
39. Нерезонансная оптическая накачка
МонохроматорЗеркало
Оптический
криостат
f=25 cm
Обрзец
Возбуждение 7 нс импульсами лазера =532 нм.
Частота повторения 5 кГц. Пятно d 50 мкм
40. Энергетические уровни конденсат поляритонов в магнитном поле
Энергии спиновых подуровней в магнитном полеРасщепление между спиновыми подуровнями конденсата
Степень циркулярной поляризации
ФЛ конденсата и экситонов в резервуаре
C. Sturm et al. PRB 2015
41. Конденсат поляритонов в микростолбиках в магнитном поле
Sturm et al. PRВ 2015.42. Зеемановское расщепление с учетом взаимодействия с резервуаром
Величина Зеемановского расщепления связана со степенью циркулярнойполяризации
J.Fischer et al.
Phys.Rev.Lett 2014, А.С. Бричкин и др ЖЭТФ 2017
43. Зеемановское расщепление vs плотность возбуждения
Зеемановское расщепление,мкэВЗеемановское расщепление vs плотность возбуждения
meV
0 meV
300
200
100
0
0
1000
Мощность возбуждения,мкВт
2000
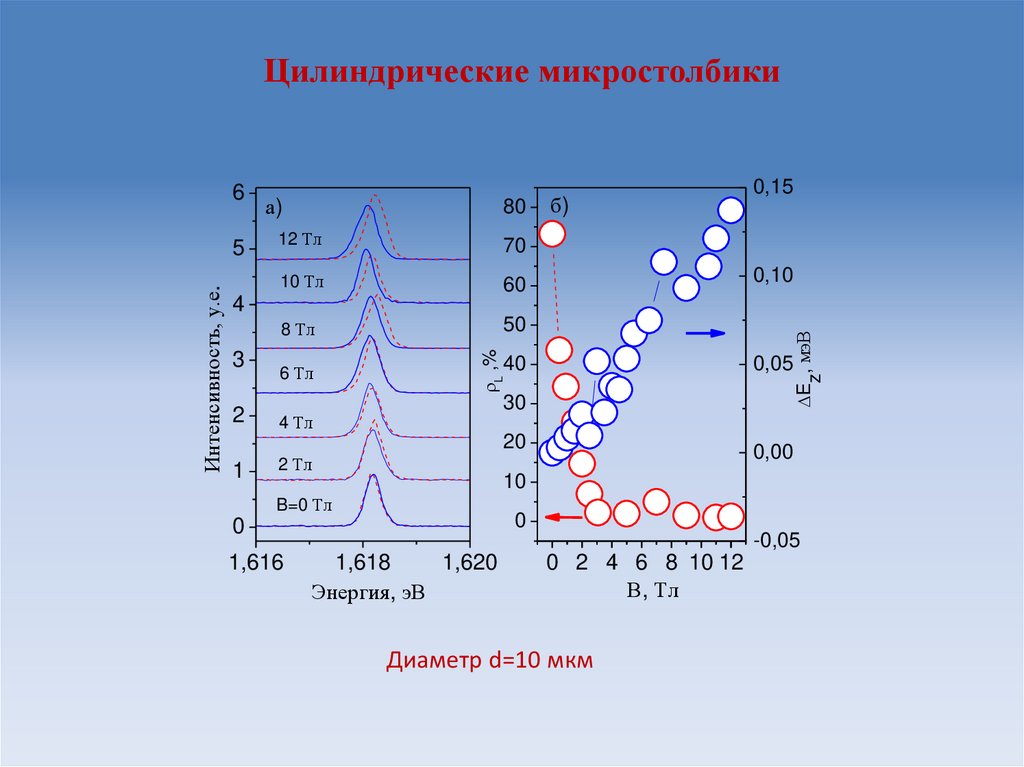
44.
Цилиндрические микростолбики80
12 Тл
70
10 Тл
60
8 Тл
50
4
3
2
6 Тл
б)
40
0,05
30
4 Тл
20
1
2 Тл
0,00
10
B=0 Тл
0
0
1,616
0,15
0,10
L ,%
Интенсивность, у.е.
5
а)
E , мэВ
z
6
-0,05
1,618
1,620
Энергия, эВ
0 2 4 6 8 10 12
В, Тл
Диаметр d=10 мкм
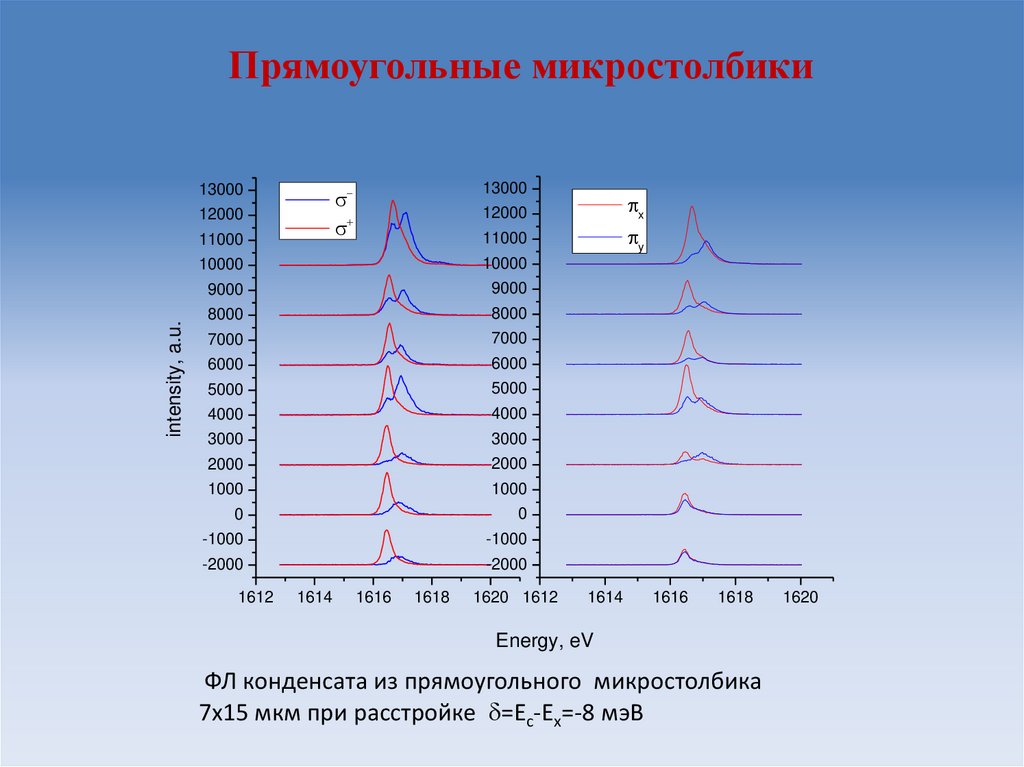
45. Прямоугольные микростолбики
1300012000
11000
intensity, a.u.
13000
12000
x
11000
y
10000
10000
9000
9000
8000
8000
7000
7000
6000
6000
5000
5000
4000
4000
3000
3000
2000
2000
1000
1000
0
0
-1000
-1000
-2000
-2000
1612
1614
1616
1618
1620 1612
1614
1616
1618
Energy, eV
ФЛ конденсата из прямоугольного микростолбика
7х15 мкм при расстройке =Ec-Eх=-8 мэВ
1620
46. Поляритонный лазер с электрической накачкой
47.
Лазер и БозерLaser –light amplification via stimulated emission of radiation
Обычный лазер
“stimulated emission”
Поляритонный «лазер» (Бозер)источник когерентного излучения
без инверсии
“stimulated scattering”
Отдельные осцилляторы изолированы.
Их когерентность устанавливается за счет
взаимодействия с излучением
Осцилляторы связаны
через поляритонполяритонное взаимодействие
48. Резюме
1.Магнитооптические измерения оказались полезны и позволили получить независимую от
других способов измерения информацию о плотности конденсата поляритонов и
константах взаимодействия.
2.
Измерения магнитофотолюминсценции микрорезонаторов содержащих GaAs/AlAs
квантовые ямы в B||0z выявили изменение знака g-фактора при переходе от линейного
режима в режим поляритонного лазера.
3.
Этот эффект оказалось возможным объяснить предположив отсутствие равновесия
между спиновыми подуровнями конденсата поляритонов, при его наличии внутри
каждого подуровня.
4.
Дополнительно был зафиксирован значительное увеличение диамагнитной
восприимчивости при переходе через порог конденсации, которое связано с
экранированием кулоновского взаимодействия экситонов в конденсате. Это позволяет
получить независимую оценку плотности конденсата, а так же констант
взаимодействия .
49. Резюме
1.Наши исследования не подтвердили необходимость учета взаимодействия поляритонов с
экситонами резервуара.
2.
Было обнаружено заметное, до 2 раз, уменьшения порога конденсации в магнитном поле.
50. Эти работы были сделаны совместно с
А.С. Бричкин, В.Д.КулаковскийИФТТ РАН
А. Rahimi-Iman, J. Fischer, A., C. Schneider, and S. Höfling
Technische Physik and Wilhelm-Conrad-Röntgen-Research Center for Complex
Material Systems, Universität Würzburg, D-97074 Würzburg, Am Hubland, Germany.
М. Дурнев, А.В. Кавокин
Лаборатория оптики спина, Институт Физики СпбГУ, С. Петербург
ФТИ им. Иоффе , С. Петербург
51.
Спасибо за внимание!52.
53. Схема мез образца
54. БЭК поляритонов в магнитном поле (теория)
( x , y )Hˆ Hˆ kin Hˆ M Hˆ int
x ( ) / 2 ,
y ( ) / 2
1 1 3
Hˆ kin *
d r
2
2m
1
Hˆ M 1 / 2 g B B d 2 r ( * )
1
Hˆ int d 3r ((U1 U 2 )( * ) 2 U 2 [ * ]2 )
2
Контактное взаимодействие
| |2 N
| |2 N
U (r1 r2 ) U 0 (r1 r2 )
V
1
3
3
(
r
)
(
r
)
U
(
r
r
)
(
r
)
(
r
)
d
r
d
r2
1
2
1
2
1
2
1
2
2
U1 1 ,U 2 ( 1 2 ) / 2 (U1 U 2 )n 1
2
1 6aB2 E0
2 0.1 1
1
Hˆ int d 3r ( 1 | |4 1 | |4 2 2 | |2 | |2 )
2
Hˆ ( e
i t /
( e i t / )
) i
t
E n B gBS z
1
( 1 2 )n 2 ( 1 2 ) S z2
4
55. Конденсат поляритонов в магнитном поле
Уравнение Гросса-Питаевскогоi
H
t
x
= Txy x x iW y + 1/2 ( 1 + 2 )
t
1
( ) x +
( 1 - 2 ) | |2 y
2
i
i
y
t
= Txy y y iW x + 1/2 ( 1 + 2 )
( ) y -
1
( 1 - 2 ) | |2 x
2
i
n -n
x
S z | | 2
2
φ W g B B
y
n | | n n
-
Эффект подавления зеемановского расщепления (парамагнитного экранирования
зеемановского расщепления ) в динамической картине можно объяснить тем, что
прецессия спинов , вызванная магнитным полем в точности компенсируется
прецессией, возникающей за счет поляритон-поляритонного взаимодействия«самоиндуцированной Ларморовской прецессии» (selfinduced Larmor rotation).
56.
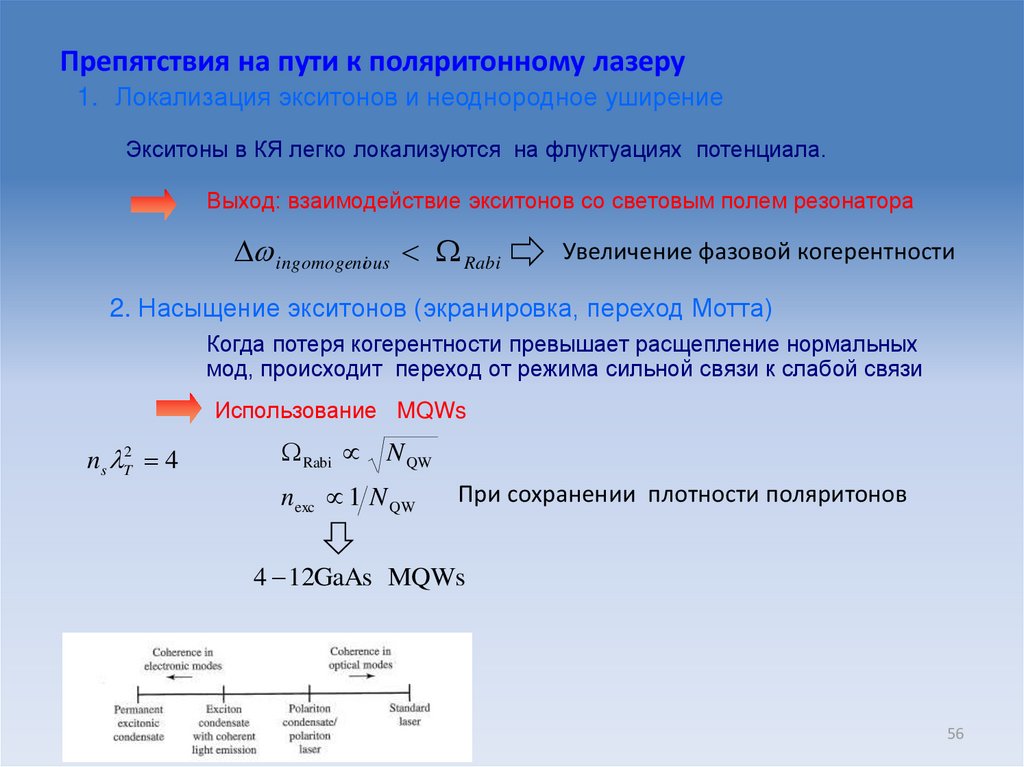
Препятствия на пути к поляритонному лазеру1. Локализация экситонов и неоднородное уширение
Экситоны в КЯ легко локализуются на флуктуациях потенциала.
Выход: взаимодействие экситонов со световым полем резонатора
ingomogenious W Rabi
Увеличение фазовой когерентности
2. Насыщение экситонов (экранировка, переход Мотта)
Когда потеря когерентности превышает расщепление нормальных
мод, происходит переход от режима сильной связи к слабой связи
Использование MQWs
n s T2 4
W Rabi N QW
nexc 1 N QW
При сохранении плотности поляритонов
4 12GaAs MQWs
56
57. Газ поляритонов в магнитном поле
Экситонная доля поляритона(коэффициент Хопфилда) зависит от
магнитного поля
1
( B)
| X ( ( B), W0 ( B)) | 1
2
( B)2 4( W0 ( B)) 2
2
Зеемановское расщепление
EZ (| X ( ( B), W0 ( B)) |2 , B) | X ( , W0 ) |2 g X B B
geff ( , W0 ) B B
Диамагнитный сдвиг экситона в КЯ
=Ec-Eex (B) расстройка( Detuning)
ħW0 (B) – расщепление Раби
растёт с полем от 10.1 до 10.6 мэВ
J.Fischer et al. PRL 2014
58. 3D Бозе-конденсат
59. Система экситонов большой плотности
Фазовая диаграмма системы экситоновСистема экситонов большой плотности
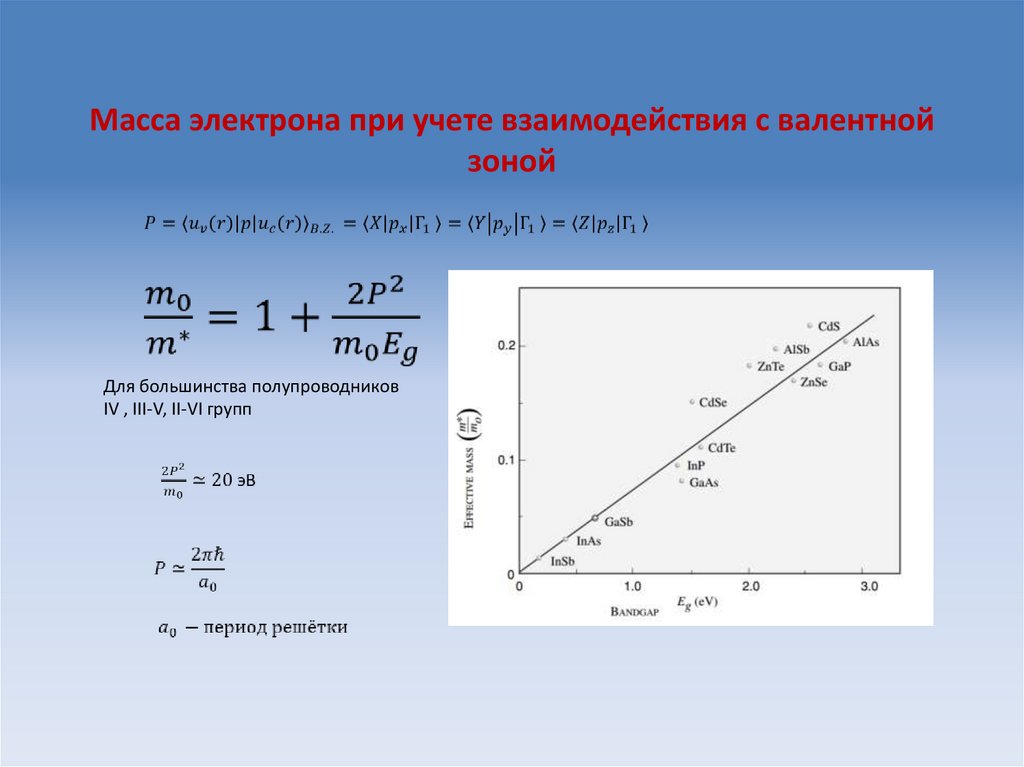
60. Масса электрона при учете взаимодействия с валентной зоной
Для большинства полупроводниковIV , III-V, II-VI групп
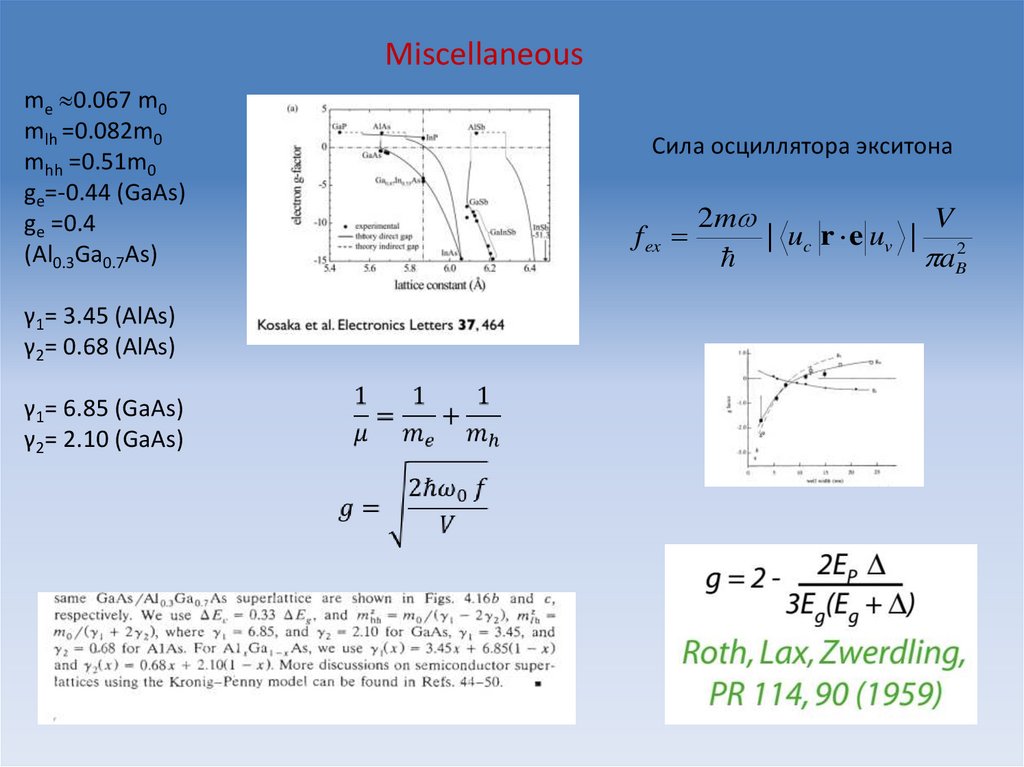
61.
Miscellaneousme 0.067 m0
mlh =0.082m0
mhh =0.51m0
ge=-0.44 (GaAs)
ge =0.4
(Al0.3Ga0.7As)
γ1= 3.45 (AlAs)
γ2= 0.68 (AlAs)
γ1= 6.85 (GaAs)
γ2= 2.10 (GaAs)
Сила осциллятора экситона
f ex
2m
V
| uc r e uv | 2
aB
62. Энергия связи и боровский радиус экситонов в зависимости от Eg
63. Dynamical Polariton BEC in magnetic field
Circ.polarization degreeDynamical Polariton BEC in magnetic field
0.2
0.0
-0.2
-0.4
-0.6
LP
dBEC
-0.8
0
1
2
3
4
Magnetic field, T
5
Circular degree of polarization circ vs B
LP
dBEC
PL spectra of the sample with P>Pth
Diamagnetic shift, eV
250
80
60
40
20
0
-20
-40
dBEC
LP
200
Zeeman splitting, eV
100
0
150
1
2
3
4
Magnetic field, T
5
100
50
0
0
5
10
15
20
25
B2 , T2
Diamagnetic shift
Zeeman splitting of the LP line and BEC
below and above Pth















































 Физика
Физика








