Динамическое программирование

1.

Динамическое
программирование
Симкина А.В.
24.10.2023
Математическая экономика, кафедра 804,
МАИ

2.

Основные идеи динамического
программирования
В основе метода динамического программирования лежит принцип оптимальности Беллмана,
формулирующийся следующим образом: управление на каждом шаге надо выбирать так, чтобы
оптимальной была сумма выигрышей на всех оставшихся до конца процесса шагах, включая
выигрыш на данном шаге.
Поясним это правило. При решении задачи динамического программирования на каждом шаге выбирается
управление, которое должно привести к оптимальному выигрышу. Бели считать все шаги независимыми
друг от друга, то оптимальным шаговым управлением будет то управление, которое приносит
максимальный выигрыш именно на данном шаге. Но, например, при покупке новой техники взамен
устаревшей на ее приобретение затрачиваются определенные средства. Поэтому прибыль от ее
эксплуатации вначале может быть небольшой. Однако в следующие годы новая техника будет приносить
большую прибыль. И наоборот, если руководитель примет решение оставить старую технику для получения
прибыли в текущем году, то в дальнейшем это приведет к значительным убыткам. Данный пример
демонстрирует следующий факт: в многошаговых процессах все шаги зависят друг от друга, и,
следовательно, управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на
весь процесс.
Другой момент, который следует учитывать при выборе управления на данном шаге, – это возможные
варианты окончания предыдущего шага: Эти варианты определяют состояние процесса. Например, при
определении количества средств, вкладываемых в предприятие в i -м году, необходимо знать, сколько
средств осталось в наличии к этому году и какая прибыль получена в предыдущем (i -1)-м году. Таким
образом, при выборе шагового управления необходимо учитывать: 1) возможные исходы предыдущего шага
и 2) влияние управления на все оставшиеся до конца процесса шаги.

3.

Задача о кратчайшем
маршруте
Введем следующие обозначения:
Пусть сij – расстояние (или стоимость переезда) от пункта i в
пункт j (на рисунке заданы числами у каждой стрелки).
Необходимо выбрать такой путь от пункта 1 до пункта 10,
для которого его длина (или общая стоимость переезда)
является минимальной.
fn(s) – стоимость, отвечающая стратегии минимальных затрат
для пути от состояния s до конечного состояния, если до него
остается n шагов;
хn(s) – решение, позволяющее достичь fn(s).
Т.е. хn(s) соответствует пути минимальной длины от состояния s
до конечного состояния, которое достигается за n шагов.
fn(s)=min (s,j)( сsj + fn-1(j)),
n=1,2,3,4

4.

Задача о кратчайшем
маршруте
fn(s)=min (s,j)( сsj + fn-1(j)),
n=1,2,3,4
Вернемся к нашему примеру. Рассмотрим последовательно все
состояния от последнего до первого.
Имеем f0(10)=0 для х0(10)= остановка.
Затем n=0
f1(8)=1+0=1 для х1(8)=10,
f1(9)=4+0=4 для х1(9)=10.

5.

Задача о кратчайшем
маршруте
fn(s)=min (s,j)( сsj + fn-1(j)),
n=1,2,3,4
Вернемся к нашему примеру. Рассмотрим последовательно все состояния от последнего до
первого.
Имеем f0(10)=0 для х0(10)= остановка.
Затем n=0
f1(8)=1+0=1 для х1(8)=10,
f1(9)=4+0=4 для х1(9)=10.
Далее
f2(5)=min(7+1,5+4)=8 для х2(5)=8,
f2(6)=min(3+1,4+4)=4 для х2(6)=8,
f2(7)=min(7+1,1+4)=5 для х2(7)=9.

6.

Задача о кратчайшем
маршруте
fn(s)=min (s,j)( сsj + fn-1(j)),
n=1,2,3,4
Затем n=0
f1(8)=1+0=1 для х1(8)=10,
f1(9)=4+0=4 для х1(9)=10.
Далее
f2(5)=min(7+1,5+4)=8 для
х2(5)=8,
f2(6)=min(3+1,4+4)=4 для
х2(6)=8,
f2(7)=min(7+1,1+4)=5 для
х2(7)=9.
Для третьего (с конца) шага имеем n=3:
f3(2)=min(10+8,12+4)=16 для х3(2)=6,
f3(3)=min(5+8,10+4,7+5)=12 для х3(3)=7,
f3(4)=min(15+4,13+5)=18 для х3(4)=7.
n=4
f4(1)=min(2+16,5+12,1+18)=17 для х4(1)=3.
Мы получили оптимальный путь (наименьшей длины
или стоимости) равный 17. Он проходит через события
1-3-7-9-10. (При последовательном рассмотрении всех
состояний оптимальные переходы выделялись
жирным шрифтом).

7.

Распределение Q средств между
N предприятиями
Пусть хn – средства, выделенные n-му предприятию; они приносят в конце года прибыль сn(хn).
Будем считать, что хn принимает только целые значения, прибыль сn(хn) не зависит от вложения средств
в другие предприятия и суммарная прибыль равна сумме прибылей, полученных от каждого
предприятия. Тогда модель имеет вид:
Найти целочисленные неотрицательные переменные хn (n=1,2,…,N), удовлетворяющие ограничению:
∑nхn = Q,
и обращающие в максимум функцию
С=∑n сn(хn).
Здесь процесс распределения средств можно рассматривать как многошаговый, номер шага совпадает с
номером предприятия;
состояние будет определяться величиной sn – количество средств, подлежащих распределению на n-м
шаге (с конца).
Обозначим fn(sn) – условную оптимальную прибыль, полученную от последних n предприятий при
распределении между ними sn средств и вычисляемую в соответствие с динамическим рекуррентным
соотношением:
fn(sn)=mах х(сn(хn) + fn-1(sn-1)), n=1,2,…,N.

8.

х
1
2
3
4
5
с4(х)
8
10
11
12
18
с3(х)
6
9
11
13
15
с2(х)
3
4
7
11
18
с1(х)
4
6
8
13
16
Распределение Q
средств между N
предприятиями
Пусть N = 4, Q =5, значения сn(хn) заданы в таблице.
Как и в предыдущем примере начинаем анализ с последнего предприятия. Индекс «1» соответствует
последнему предприятию, а индекс «4» – первому. Для n=1 прибыль проставлена в последней колонке.
Для n=2
f2(0)=mах[с2(0)+f1(0)]=0
при x2(0)=0,
f2(1)=mах[с2(1)+f1(0),с2(0)+f1(1)]=mах[3+0,0+4]=4
при x2(1)=0,
f2(2)=mах[с2(2)+f1(0),c2(1)+f1(1),с2(0)+f1(2)]=
Из 1 миллиона во второе
=mах[4+0,3+4,0+6]=7
при xпредприятие
2(2)=1,
с конца вкладываем
f2(3)=mах[с2(3)+f1(0),с2(2)+f1(1),с2(1)+f1(2),с2(0)+f1(3)]=
0
=mах[7+0,4+4,3+6,0+8]=9
при x2(3)=1,
f2(4)=mах[с2(4)+f1(0),с2(3)+f1(1),с2(2)+f1(2),с2(1)+f1(3),с2(0)+f1(4)]=
=mах[11+0,7+4,4+6,3+8,0+13]=13
при х2(4)=0,
f2(5)=mах[с2(5)+f1(0),с2(4)+f1(1),с2(3)+f1(2),с2(2)+f1(3),с2(1)+f1(4),с2(0)+f1(5)]
=mах[18+0,11+4,7+6,4+8,3+13,0+16]=18
при x2(5)=5.

9.

х
1
2
3
4
5
с4(х)
8
10
11
12
18
с3(х)
6
9
11
13
15
с2(х)
3
4
7
11
18
с1(х)
4
6
8
13
16
Распределение Q
средств между N
предприятиями
Пусть N = 4, Q =5, значения сn(хn) заданы в таблице.
Как и в предыдущем примере начинаем анализ с последнего предприятия. Индекс «1» соответствует
последнему предприятию, а индекс «4» – первому. Для n=1 прибыль проставлена в последней колонке.
Для n=2
f2(0)=mах[с2(0)+f1(0)]=0
при x2(0)=0,
f2(1)=mах[с2(1)+f1(0),с2(0)+f1(1)]=mах[3+0,0+4]=4
при x2(1)=0,
f2(2)=mах[с2(2)+f1(0),c2(1)+f1(1),с2(0)+f1(2)]=
=mах[4+0,3+4,0+6]=7
при x2(2)=1,
f2(3)=mах[с2(3)+f1(0),с2(2)+f1(1),с2(1)+f1(2),с2(0)+f1(3)]=
=mах[7+0,4+4,3+6,0+8]=9
при x2(3)=1,
f2(4)=mах[с2(4)+f1(0),с2(3)+f1(1),с2(2)+f1(2),с2(1)+f1(3),с2(0)+f1(4)]=
=mах[11+0,7+4,4+6,3+8,0+13]=13
при х2(4)=0,
f2(5)=mах[с2(5)+f1(0),с2(4)+f1(1),с2(3)+f1(2),с2(2)+f1(3),с2(1)+f1(4),с2(0)+f1(5)]
=mах[18+0,11+4,7+6,4+8,3+13,0+16]=18
при x2(5)=5.

10.

х
1
2
3
4
5
с4(х)
8
10
11
12
18
с3(х)
6
9
11
13
15
с2(х)
3
4
7
11
18
с1(х)
4
6
8
13
16
Распределение Q
средств между N
предприятиями
Пусть N = 4, Q =5, значения сn(хn) заданы в таблице.
Как и в предыдущем примере начинаем анализ с последнего предприятия. Индекс «1» соответствует
последнему предприятию, а индекс «4» – первому. Для n=1 прибыль проставлена в последней колонке.
Для n=2
f2(0)=mах[с2(0)+f1(0)]=0
при x2(0)=0,
f2(1)=mах[с2(1)+f1(0),с2(0)+f1(1)]=mах[3+0,0+4]=4
при x2(1)=0,
f2(2)=mах[с2(2)+f1(0),c2(1)+f1(1),с2(0)+f1(2)]=
=mах[4+0,3+4,0+6]=7
при x2(2)=1,
f2(3)=mах[с2(3)+f1(0),с2(2)+f1(1),с2(1)+f1(2),с2(0)+f1(3)]=
=mах[7+0,4+4,3+6,0+8]=9
при x2(3)=1,
f2(4)=mах[с2(4)+f1(0),с2(3)+f1(1),с2(2)+f1(2),с2(1)+f1(3),с2(0)+f1(4)]=
=mах[11+0,7+4,4+6,3+8,0+13]=13
при х2(4)=0,
f2(5)=mах[с2(5)+f1(0),с2(4)+f1(1),с2(3)+f1(2),с2(2)+f1(3),с2(1)+f1(4),с2(0)+f1(5)]
=mах[18+0,11+4,7+6,4+8,3+13,0+16]=18
при x2(5)=5.

11.

х
1
2
3
4
5
с4(х)
8
10
11
12
18
с3(х)
6
9
11
13
15
с2(х)
3
4
7
11
18
с1(х)
4
6
8
13
16
Распределение Q
средств между N
предприятиями
Для n=2
f2(0)=0
при x2(0)=0,
f2(1)=4
при x2(1)=0,
f2(2)=7
при x2(2)=1,
f2(3)=9
при x2(3)=1,
f2(4)=13
при х2(4)=0,
f2(5)=18
при x2(5)=5.
Для n=3
f3(0)=mах[с3(0)+f2(0)]=0
при x3(0)=0,
f3(1)=mах[с3(1)+f2(0),с3(0)+f2(1)]=mах[6+0,0+4]=6
при x3(1)=1,
f3(2)=mах[с3(2)+f2(0),c3(1)+f2(1),с3(0)+f2(2)]=
=mах[9+0,6+4,0+7]=10
при x3(2)=1,
f3(3)=mах[с3(3)+f2(0),с3(2)+f2(1),с3(1)+f2(2),с3(0)+f2(3)]=
=mах[11+0,9+4,6+7,0+9]=13
при x3(3)=1 или 2,
f3(4)=mах[с3(4)+f2(0),с3(3)+f2(1),с3(2)+f2(2),с3(1)+f2(3),с3(0)+f2(4)]=
=mах[13+0,11+4,9+7,6+9,0+13]=16
при х3(4)=2,
f3(5)=mах[с3(5)+f2(0),с3(4)+f2(1),с3(3)+f2(2),с3(2)+f2(3),с3(1)+f2(4),с3(0)+f2(5)]
=mах[15+0,13+4,11+7,9+9,6+13,0+18]=19
при x3(5)=1.

12.

х
1
2
3
4
5
с4(х)
8
10
11
12
18
с3(х)
6
9
11
13
15
с2(х)
3
4
7
11
18
с1(х)
4
6
8
13
16
Распределение Q
средств между N
предприятиями
И, наконец, для n=4
f4(0)=mах[с4(0)+f3(0)]=0
при x 4(0)=0,
f4(1)=mах[с4(1)+f3(0),с4(0)+f3(1)]=mах[8+0,0+6]=8
при x4(1)=1,
f4(2)=mах[с4(2)+f3(0),c4(1)+f3(1),с4(0)+f3(2)]=
=mах10+0,8+6,0+10]=14
при x4(2)=1,
f4(3)=mах[с4(3)+f3(0),с4(2)+f3(1),с4(1)+f3(2),с4(0)+f3(3)]=
=mах[11+0,10+6,8+10,0+13]=18
при x4(3)=1,
f4(4)=mах[с4(4)+f3(0),с4(3)+f3(1),с4(2)+f3(2),с4(1)+f3(3),с4(0)+f3(4)]=
=mах[12+0,11+6,10+10,8+13,0+16]=21
при х4(4)=1,
f4(5)=mах[с4(5)+f3(0),с4(4)+f3(1),с4(3)+f3(2),с4(2)+f3(3),с4(1)+f3(4),с4(0)+f3(5)]
=mах[18+0,12+6,11+10,10+13,8+16,0+19]=24
при x4(5)=1.
Теперь соберем оптимальное решение (при последовательном рассмотрении всех
состояний оптимальные переходы подчеркивались):
Для первого предприятия, когда s4=5, видим, что x4(5)=1, значит, первое предприятие
получает 1 и остается s3=s4–x4(5)=5–1=4. Находим лучшее размещение средств для
второго предприятия (на третьем с конца шаге) при s3=4. Это х3(4)=2, остается s2=s3–
x3(4)=4–2=2. На втором (с конца) шаге x2(2)=1 и на последнее предприятие (первый с
конца шаг) остается s1= s2 – x2(2)=2–1=1 и x1(1)=1.
Максимум суммарной прибыли равен 24 у.е.
Для n=2
f2(0)=0
f2(1)=4
f2(2)=7
f2(3)=9
f2(4)=13
f2(5)=18
Для n=3
f3(0)=0
f3(1)=6
f3(2)=10
f3(3) =13
или 2,
f3(4)=16
f3(5)=19
при x2(0)=0,
при x2(1)=0,
при x2(2)=1,
при x2(3)=1,
при х2(4)=0,
при x2(5)=5.
при x3(0)=0,
при x3(1)=1,
при x3(2)=1,
при x3(3)=1
при х3(4)=2,
при x3(5)=1.

13.

Задача управления запасами
Необходимо разработать такую календарную программу выпуска изделия на плановый период, состоящий из Т временных
отрезков, при которой общая сумма затрат на производство и на содержание запасов минимизируется при условии полного и
своевременного удовлетворения спроса. Обозначим:
dn – спрос на отрезке n от конца;
cn(x,s) – затраты на отрезке n, связанные с выпуском х единиц изделия и с содержанием запасов, объем которых на конец
отрезка равен s единиц. В этой системе обозначений подстрочный индекс «1» соответствует конечному, а «Т» – начальному
состоянию.
Состояние системы в начале каждого отрезка определяется уровнем запасов, поэтому для принятия решения об объеме
выпуска не нужно знать, каким образом достигнут этот уровень, т.е. опять же имеем систему без обратной связи.
Пусть fn(s) – стоимость, отвечающая стратегии минимальных затрат на n оставшихся отрезках при уровне запасов s на начало
n-го от конца отрезка;
xn(s) – объем выпуска, обеспечивающий достижение fn(s).
Пусть уровень запасов на конец планового периода равен нулю, тогда при уровне запасов s на начало последнего (1-го от
конца) отрезка выпуск x1(s)=d1–s и
f1(s)= c1(x,0)= c1(d1 – s,0), s=0,1,…,d1.
Заметим, что если начальный уровень запасов отрезка n равен s, а объем выпуска – х, то величина (s+х–dn) – есть уровень
запасов на конец данного отрезка, отсюда получаем общее рекуррентное соотношение в виде:
fn(s) = minx[cn(x, s+х–dn)+ fn-1(s+х–dn)], n=1,…,Т, s=0,1,…,d1+…+ dn.
Для упрощения вычислений предположим, что производственные мощности и складские площади ограничены, пусть
х=0,1,…,5 и s=0,1,…,4. Допустим также, что спрос и затраты постоянны во времени, и пусть dn=3, а cn(x, s)= c(x)+hs, где первое
слагаемое относится к производству, а второе определяется стоимостью содержания запасов (арендная плата за складские
помещения, проценты за кредит для создания запасов, страховые взносы и собственно расходы по содержанию запасов).

14.

Задача управления запасами
Для упрощения вычислений предположим, что производственные мощности и
складские площади ограничены, пусть х=0,1,…,5 и s=0,1,…,4. Допустим
также, что спрос и затраты постоянны во времени, и пусть dn=3, а cn(x, s)=
c(x)+hs, где первое слагаемое относится к производству, а второе определяется
стоимостью содержания запасов (арендная плата за складские помещения,
проценты за кредит для создания запасов, страховые взносы и собственно
расходы по содержанию запасов).
Пусть с(0)=0, с(1)=15, с(2)=17, с(3)=19,с(4)=21, с(5)=23; h=1.
Для n=1
f1(0)=с(3-0)=с(3)=19 при x1(0)=3,
f1(1)=с(3-1)=с(2)=17 при x1(1)=2,
Пусть уровень запасов на конец
планового периода равен нулю, тогда
f1(2)=с(3-2)=с(1)=15 при x1(2)=1,
при уровне запасов s на начало
f1(3)=с(0)=0 при x1(3)=0.
последнего (1-го от конца) отрезка
fn(s) = minx[cn(x, s+х–dn)+ fn-1(s+х–dn)],
n=1,…,Т, s=0,1,…,d1+…+ dn.
выпуск x1(s)=d1–s и
f1(s)= c1(x,0)= c1(d1 – s,0),
s=0,1,…,d1.

15.

Задача управления запасами
Пусть с(0)=0, с(1)=15, с(2)=17, с(3)=19,с(4)=21, с(5)=23; h=1.
Для n=1
f1(0)=с(3)=19 при x1(0)=3,
cn(x, s)= c(x)+hs
f1(1)=с(2)=17 при x1(1)=2,
f1(2)=с(1)=15 при x1(2)=1, один товар остаётся на складе,
f1(3)=с(0)=0 при x1(3)=0. поэтому оплачиваем склад
Для n=2
f2(0)=min[с(3)+1·0+f1(0),c(4)+1·1+f1(1),c(5)+1·2+f1(2)] =min[19+19,21+1+17,23+2+15]=38 при x2(0)=3,
f2(1)=min[с(2)+1·0+f1(0),c(3)+1·1+f1(1),c(4)+1·2+f1(2),c(5)+1·3+f1(3)]=min[17+19,19+1+17,21+2+15,23+3+0]=26
при x2(1)=5,
f2(2)=min[с(1)+0+f1(0),c(2)+1+f1(1),c(3)+2+f1(2),c(4)+3+f1(3)]= min[15+19,17+1+17,19+2+15,21+3+0]=24
при x2(2)=4,
f2(3)=min[с(0)+0+f1(0),c(1)+1+f1(1),c(2)+2+f1(2),c(3)+3+f1(3)]=min[0+19,15+1+17,17+2+15,19+3+0]=19
при x2(3)=0,
f2(4)=min[с(0)+1+f1(1),c(1)+2+f1(2),c(2)+3+f1(3)]=min[0+1+17,15+2+15,17+3+0]=18 при x2(4)=0.
4 товара на складе, можем ничего не
производить нового, выпустить 3 товара на
рынок, а 1 останется про запас
Не оставляем на складе на последний период больше 3
товаров, потому что нам останется продать только 3.

16.

Задача управления запасами
Для n=1
f1(0)=с(3)=19 при x1(0)=3,
f1(1)=с(2)=17 при x1(1)=2,
f1(2)=с(1)=15 при x1(2)=1,
f1(3)=с(0)=0 при x1(3)=0.
Для n=2
f2(0)=38 при x2(0)=3,
Производственная мощность
f2(1)=26 при x2(1)=5,
ограничена 5 товарами
f2(2)=24 при x2(2)=4,
f2(3)=19 при x2(3)=0,
f2(4)=18 при x2(4)=0.
Для n=3 f3(0)=min[с(3)+0+f2(0),c(4)+1+f2(1),c(5)+2+f2(2)]=min[19+38,21+1+26,23+2+24]=48 при x3(0)=4,
f3(1)=min[с(2)+0+f2(0),c(3)+1+f2(1),c(4)+2+f2(2),c(5)+3+f2(3)]=min[17+38,19+1+26,21+2+24,23+3+19]=45 при x3(1)=5,
f3(2)=min[с(1)+f2(0),c(2)+1+f2(1),c(3)+2+f2(2),c(4)+3+f2(3),c(5)+4+f2(4)]=min[15+38,18+26,21+24,24+19,23+4+18]=43
при x3(2)=4,
f3(3)=min[с(0)+0+f2(0),c(1)+1+f2(1),c(2)+2+f2(2),c(3)+3+f2(3),c(4)+4+f2(4)]=min[0+38,16+26,19+24,22+19,25+18]=38
при x3(3)=0,
f3(4)=min[с(0)+1+f2(1),c(1)+2+f2(2),c(2)+3+f2(3),c(3)+4+ f2(4)]=min[1+26,17+24,20+19,23+18]=27 при x3(4)=0.
На складе максимум умещается 4 товара

17.

Задача управления Таблица
запасами
для всех 8 периодов
Для n=1
f1(0)=с(3)=19 при x1(0)=3,
f1(1)=с(2)=17 при x1(1)=2,
f1(2)=с(1)=15 при x1(2)=1,
f1(3)=с(0)=0 при x1(3)=0.
Для n=2
f2(0)=38 при x2(0)=3,
f2(1)=26 при x2(1)=5,
f2(2)=24 при x2(2)=4,
f2(3)=19 при x2(3)=0,
f2(4)=18 при x2(4)=0.
Для n=3 f3(0)=48 при x3(0)=4,
f3(1)=45 при x3(1)=5,
f3(2)=43 при x3(2)=4,
f3(3)=38 при x3(3)=0,
f3(4)= 27 при x3(4)=0.
s
0
n=1
х1
f1
3
19
n=2
x2
f2
3
38
n=3
x3
f3
4
48
n=4
x4
f4
3,4 67
n=5
x5
f5
5
79
n=6
x6
f6
4
96
n=7
x7
f7
3,4 11
5
n=8
x8
f8
5
127
1
2
17
5
26
5
45
5
64
5
74
5
93
5
10
6
5
123
2
1
15
4
24
4
43
5
54
4
72
4
91
5
10
2
4
120
3
0
0
0
19
0
38
0
48
0
67
0
79
0
96
0
115
0
18
0
27
0
46
0
65
0
75
0
94
0
107
4
И, наконец, для n=4
f4(0)=min[с(3)+0+f3(0),c(4)+1+f3(1),c(5)+2+f3(2)]=min[19+48,21+1+45,23+2+43]=67 при x4(0)=3 или 4,
f4(1)=min[с(2)+0+f3(0),c(3)+1+f3(1),c(4)+2+f3(2),c(5)+3+f3(3)]=min[17+48,19+1+46,21+2+43,23+3+38]=64 при x4(1)=5,
f4(2)=min[с(1)+f3(0),c(2)+1+f3(1),c(3)+2+f3(2),c(4)+3+f3(3),c(5)+4+f3(4)]=min[15+48,18+45,21+43,24+38,23+4+27]=54 при x4(2)=5,
f4(3)=min[с(0)+0+f3(0),c(1)+1+f3(1),c(2)+2+f3(2),c(3)+3+f3(3),c(4)+4+f3(4)]=min[0+48,16+45,19+43,22+38,25+27]=48 при x4(3)=0,
f4(4)=min[с(0)+1+f3(1),c(1)+2+f3(2),c(2)+3+f3(3),c(3)+4+ f3(4)]=min[1+45,17+43,20+38,23+27]=46 при x4(4)=0.

18.

Теперь, задаваясь различным уровнем запасов на начало планового периода, можно определить оптимальные стратегии для
любого Т от 1 до 8. Так, например, если исходный уровень запасов на начало планового периода равен нулю, то оптимальный
календарный план при Т=4 будет:
x4(0)=3, x3(0)=4, x2(1)=5, x1(3)=0 или
x4(0)=4, x3(1)=5, x2(3)=0, x1(0)=3
и минимальная общая сумма затрат составит 67.
Пусть Т=8, тогда минимальная общая сумма затрат составит 127 и x8(0)=5, останется на следующий отрезок 5-3=2, имеем x7(2)=5,
значит на следующий отрезок останется 2+5-3=4 и x6(4)=0, останется 4-3=1 и x5(1)=5, останется 1+5-3=3, x4(3)=0, останется 3-3=0,
x3(0)=4, останется 4-3=1, x2(1)=5, останется 1+5-3=3 и x1(3)=0.
В таблицу сведем оптимальные
стратегии (планы выпуска) для
плановых периодов длительностью Т
и начальным уровнем запасов
равным нулю.
Обратим внимание на Т=4.
Здесь два оптимальных решения,
дающих минимальные затраты 67.
При Т=7 имеем три решения с
одинаковым значением целевой
функции 115.
Плановый
период
Т
n=8
янв
n=7
фев
1
2
3
4
3
3
4
3
4
5
4
3
4
4
5
3
5
4
5
5
5
4
5
5
5
5
6
7
8
n=6
мар
0
5
0
0
0
5
0
0
0
n=5
апр
0
3
5
4
0
3
4
5
n=4
май
0
5
4
4
5
0
n=3
ию
н
0
5
5
0
4
n=2
ию
л
0
0
3
5
n=1
авг
0
Общая
сумма
затрат
Среднемесячные
затраты
19
38
48
67
19
19
16
16.75
79
96
15.8
16
115
16.43
127
15.9

19.

Задача замены оборудования
Пусть величина cij представляет собой сумму покупной цены и ожидаемых расходов на ремонт и обслуживание оборудования, приобретенного в
начале года i, за вычетом остаточной стоимости этого оборудования на начало года j.
fi – величина затрат, соответствующая стратегии замены, минимизирующей эти затраты в интервалах i, i+1,…, n, в предположении, что новое
оборудование приобретается в год i.
Тогда для нахождения оптимальной стратегии нам необходимо вычислить f1(минимальные затраты и соответствующую стратегию с первого шага),
пользуясь следующим рекуррентным соотношением:
fn+1 =0,
fi =minj>i{cij + fj}, i=n, n–1, …, 1.
Предположим, что затраты, отвечающие некоторой стратегии замены, включают две составляющие:
рik – стоимость замены оборудования возраста k на интервале i за вычетом его остаточной стоимости;
rik – стоимость эксплуатации оборудования возраста k на интервале i.
Пусть fi(k) – стратегия, минимизирующая затраты на интервалах i, i+1,…, n, при условии, что в начале интервала i возраст оборудования составляет k
лет.
Если оптимальное решение состоит в сохранении оборудования в интервале i, то
fi(k) =rik+1 +fi+1(k+1),
но если оптимальное решение сводится к его замене, то
fi(k) =рik +ri1 +fi+1(1).
Таким образом, имеем
fi(k)=min{rik+1+fi+1(k+1),рik+ri1+fi+1(1)}, i=1,2,…,n,
где fn+1(k)=0 для всех k. Пусть К – возможный срок службы оборудования.
Мы планируем на n лет, поэтому начало (n+1)-го периода соответствует концу нашего планового периода.
Нахождение оптимального решения заключается в вычислении f1(k0), где k0 – возраст оборудования на начало планового периода. Если в это
время рассматриваемая единица оборудования отсутствует, то нет смысла говорить о его сохранении при i=1, а решение о замене есть просто
покупка нового оборудования.

20.

Задача
замены
оборудования
fi(k)=min{rik+1+fi+1(k+1),рik
+ri1+fi+1(1)}, i=1,2,…,n,
Необходимо составить план замены
оборудования на пять лет при условии
отсутствия его в начале первого года,
прогнозируемые затраты сведены в
1
2 слева
3
4 rik,5 справа pik)
1
2
3
таблицы(
1
20
2
3
4
18
16
14
36
32
28
68
52
120
5
10
20
40
85
200
1
100
2
3
4
55
60
65
80
85
105
5
70
90
110
4
115
Пустые клетки в таблицах образовались из того факта, что в начале планового периода оборудования нет, оно только
приобретается, поэтому нет нужды прогнозировать некоторые затраты, например, в год 3 не будет оборудования с возрастом 4 или на
начало любого года не будет оборудования с пятилетним возрастом.
f6(k) =0 для всех k.
i=5 (в начале года 5 возраст не может быть больше 4):
f5(4) =min{r55 +f6(5), р54 +r51 +f6(1)}=min{200+0,115+10+0}=125,
f5(3) =min{r54 +f6(4), р53 +r51 +f6(1)}=min{85+0,110+10+0}=85,
f5(2) =min{r53 +f6(3), р52 +r51 +f6(1)}=min{40+0,90+10+0}=40,
f5(1) =min{r52 +f6(2), р51 +r51 +f6(1)}=min{20+0,70+10+0}=20.

21.

fi(k)=min{rik+1+fi+1(k+1),рik
+ri1+fi+1(1)}, i=1,2,…,n,
f6(k) =0 для всех k.
1
20
2
1
3
4
2
3
4
18
16
14
36
32
28
68
52
120
5
10
20
40
85
5
200
1
1
100
2
3
4
5
i=5
f5(4) =min{r55 +f6(5), р54 +r51 +f6(1)}=min{200+0,115+10+0}=125,
f5(3) =min{r54 +f6(4), р53 +r51 +f6(1)}=min{85+0,110+10+0}=85,
f5(2) =min{r53 +f6(3), р52 +r51 +f6(1)}=min{40+0,90+10+0}=40,
f5(1) =min{r52 +f6(2), р51 +r51 +f6(1)}=min{20+0,70+10+0}=20.
i=4 (в начале года 4 возраст не может быть больше 3):
f4(3) =min{r44 +f5(4), р43 +r41 +f5(1)}=min{120+125,105+14+20}=139,
f4(2) =min{r43 +f5(3), р42 +r41 +f5(1)}=min{52+85,85+14+20}=119,
f4(1) =min{r42 +f5(2), р41 +r41 +f5(1)}=min{28+40,65+14+20}=68.
i=3 (в начале года 3 возраст не может быть больше 2):
f3(2) =min{r33 +f4(3), р32 +r31 +f4(1)}=min{68+139,80+16+68}=164,
f3(1) =min{r32 +f4(2), р31 +r31 +f4(1)}=min{32+119,60+16+68}=144.
i=2 (в начале года 2 возраст не может быть больше 1):
f2(1) =min{r22 +f3(2), р21 +r21 +f3(1)}=min{36+164,55+18+144}=200.
Т.к. по условию примера в начале первого года мы приобретаем новое оборудование, то
f1(0) = р11 +r11 +f2(1)=100+20+200=320.
Таким образом, оптимальная стратегия заключается в следующем:
В начале третьего года заменяем оборудование, купленное в начале первого года,
и эксплуатируем его до конца планового периода.
2
3
55
60
65
80
85
105
70
90
110
4
115

22.

Задача о рюкзаке с
повторениями
Начнём с варианта с повторениями. Как обычно, важно правильно выбрать подзадачи. В
данном случае есть два естественных способа: рассмотреть рюкзак меньшей
вместимости w⩽W или же меньшее число товаров (скажем, товары 1,2,…,j, где j ⩽n). Для
того чтобы понять, какой подход действительно работает, обычно приходится немного
поэкспериментировать. Попробуем взять рюкзак меньшей вместимости и положим
V[w]=максимально возможная стоимость для рюкзака ёмкости w.
Можем ли мы выразить V[w] через ответы для меньших подзадач? Ясно, что если в
оптимальное заполнение рюкзака ёмкости w входит товар i, то без одной штуки этого товара
мы получим оптимальное заполнение рюкзака ёмкости w−wi. Другими словами, V[w] — это
просто V[w−wi]+vi для некоторого i. Мы не знаем, для какого именно i, поэтому нам нужно
перебрать все возможные варианты:
V[w]=max i:wi​⩽w​{V[w−wi​]+vi​},
где, как обычно, максимум по пустому множеству считается равным 0.

23.

Случай А. Рюкзак с повторениями (Неограниченный рюкзак)
Пусть вместимость рюкзака W=4
Предмет
Объем
Ценность
1 (Очки)
1
1
2 (Ножницы)
2
4
3 (Кошелек)
3
6
Решим задачу.
Согласно методу динамического программирования, надо
рассмотреть подзадачи. Если мы рассматриваем рюкзак
вместимости 0, то ничего туда положить нельзя.
Ценность
Предметы
0
0
1
2
3
4
Рассмотрим рюкзак вместимости 1. Туда
можно положить очки.
Ценность
Предметы
0
0
1
1
Очки
2
3
4

24.

Рассмотрим рюкзак вместимости 2. Туда можно положить или две пары очков или одни
ножницы. У пары очков ценность 2, а у ножниц 4, выбираем ножницы.
0
0
Ценность
Предметы
1
1
Очки
2
4
Ножницы
3
4
Рассмотрим рюкзак вместимости 3. Туда можно положить или очки и ножницы
или кошелек. У ножниц с очками ценность 5, у кошелька 6, кладём кошелек.
Ценность
Предметы
0
0
1
1
Очки
2
4
Ножницы
3
6
Кошелек
4
Рассмотрим рюкзак вместимости 4. Туда можно положить кошелек с очками или две
пары ножниц. У кошелька с очками ценность 7, у двух пар ножниц 8, кладём ножницы.
Ценность
Предметы
0
0
1
1
Очки
2
4
Ножницы
Итого: в рюкзаке две пары ножниц с
общей ценностью 8.
3
6
Кошелек
4
8
Ножницы,
ножницы

25.

Рюкзак без повторений
Теперь рассмотрим вариант задачи, когда каждый товар есть в одном
экземпляре. Тогда воспользоваться подзадачами из прошлого решения
не удаётся, поскольку надо как-то учитывать, что мы уже взяли.
Сделаем это, добавив второй параметр 0⩽j⩽n: обозначим
через V[w,j] максимальную стоимость унесённого, если разрешается
уносить лишь товары 1,…,j и общий вес должен быть не больше W.
Исходная задача: найти V[W,n].
Теперь нужно научиться выражать V[w,j] через результаты для
меньших подзадач. Это несложно. В оптимальном заполнении
товар j либо участвует, либо нет:
V[w,j]=max{V[w−wj​,j−1]+vj​,V[w,j−1]}
(первый член берётся, только если wj⩽w.) Другими словами, можно
выразить V[w,j] через результаты подзадач V[⋅,j−1].

26.

Рюкзак с повторениями
Пусть у нас есть рюкзак с вместимостью W=3.
Предмет
Объем
Ценность
Очки
1
1
Ножницы
2
4
Кошелек
3
6
По методу динамического программирования необходимо рассмотреть
подзадачи с рюкзаками меньшей вместимости.
Если у рюкзака вместимость 0, ничего
положить не можем.
Очки
Очки и
ножницы
Очки, ножницы,
кошелек
x=0
x=1
x=2
0
0
0
0
x=3
0
1
0
2
0
3
0

27.

Теперь рассмотрим рюкзак размерности 1. Там до этого ничего не лежало,
мы можем положить очки, когда в распоряжении только очки.
Если в распоряжении есть очки и ножницы, а в рюкзаке уже лежат очки, то к
ним ничего доложить не получится.
Если в распоряжении очки, ножницы и кошелек, а в рюкзаке лежат уже очки
(ножницы положить не получилось), то кошелек в рюкзак доложить не
получится.
Ценность очков равна 1.
Очки
Очки и
ножницы
Очки, ножницы,
кошелек
x=0
x=1
x=2
0
0
0
0
1
0
1
1
x=3
0
1
2
0
3
0

28.

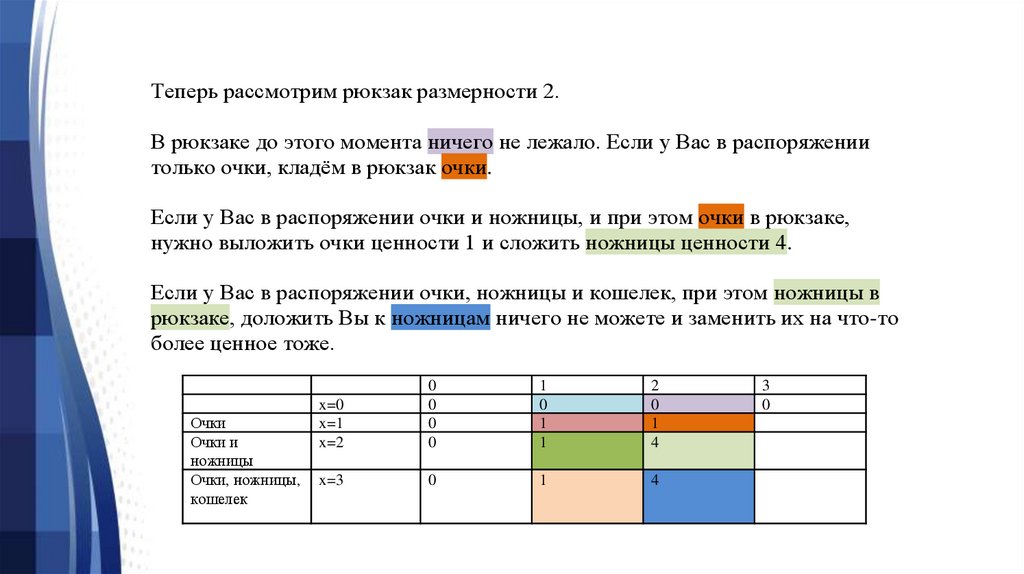
Теперь рассмотрим рюкзак размерности 2.
В рюкзаке до этого момента ничего не лежало. Если у Вас в распоряжении
только очки, кладём в рюкзак очки.
Если у Вас в распоряжении очки и ножницы, и при этом очки в рюкзаке,
нужно выложить очки ценности 1 и сложить ножницы ценности 4.
Если у Вас в распоряжении очки, ножницы и кошелек, при этом ножницы в
рюкзаке, доложить Вы к ножницам ничего не можете и заменить их на что-то
более ценное тоже.
Очки
Очки и
ножницы
Очки, ножницы,
кошелек
x=0
x=1
x=2
0
0
0
0
1
0
1
1
2
0
1
4
x=3
0
1
4
3
0

29.

Рассмотрим рюкзак вместимости 3.
Если у Вас в распоряжении очки, а до этого в рюкзаке ничего не было, то
кладём очки.
Если у Вас в распоряжении ножницы и очки, а очки уже в рюкзаке, то можно
доложить ножницы, тогда суммарно ценность будет 1+4.
Если у Вас в распоряжении ножницы, очки и кошелек, а очки и ножницы в
рюкзаке, можно оставить их или можно положить вместо ножниц и очков
кошелек, у которого ценность выше и равна 6. Выбираем кошелек.
Очки
Очки и
ножницы
Очки, ножницы,
кошелек
x=0
x=1
x=2
0
0
0
0
1
0
1
1
2
0
1
4
3
0
1
5
x=3
0
1
4
6

30.

Для того, чтобы при программировании нам было легче восстановить ответ, составим еще одну матрицутаблицу К, в которой будем ставить 1, если предмет кладём и 0, если не кладём.
Для реконструкции решения проходим по вспомогательной таблице-матрице К от
нижней правой ячейки до верхней строки. Для текущей ячейки К[i,j]
- Если К[i,j]=1, то включаем i-й предмет в решение и переходим к ячейке [i-1,j-wi]
- Если K[i,j]=0, то не включаем i-й предмет в решение и переходим к ячейке [i-1,j].
Итого: в рюкзаке кошелек с ценностью 6.