Похожие презентации:
Линейное программирование
1.
Линейное программированиеДля ст-ов ЭИФ, 4-ый семестр
Часть 1
2.
Литература:1. Карпелевич и Садовский. Элементы линейной
алгебры и линейного программирования
2. Красс и Чупрынов. Основы математики и ее
приложения в экономическом образовании
3. Заславский. Сборник задач по линейному
программированию
4. Рогов. Метод. указания по дисциплине «Высшая
математика» раздел «Математическое
программирование
3.
1.Системы линейных уравненийи неравенств
1.1. Am n X B,
a11
a21
Am n
a
m1
x1
x2
X ,
x
n
a1n
a22 a2 n
,
am 2 amn
b1
b2
B .
b
m
a12
4.
a11 x1 a12 x2 a1n xn b1a x a x a x b
21 1 22 2
2n n
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
am1 x1 am 2 x2 amn xn bm
5.
r = rank A = rank A < min {m,n},x1, ,xr -- базисные неизвестные,
xr+1, …,xn -- свободные неизвестные и
Пусть
x1 1 1r 1 xr 1 1n xn
x x x
2
2
2 r 1 r 1
2n n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
xr r rr 1 xr 1 rn xn .
Определение базисного решения
X ( 1, 2 , , r ,0,0, ,0).
6.
Метод Гаусса. Примерx1 2 x2 x3 x4 1
2 x1 3 x2 x3 2 x4 8
x x 2 x 3x 7
3
4
1 2
Прямой ход метода Гаусса
1 2 1 1 1 1 2 1 1 1
A 2 3 1 2 8 0 1 3 4 6
1 1 2 3 7 0 1 3 4 6
7.
1 2 1 1 10 1 3 4 6
x3
x1 2 x2 1
x2
6 3 x3
x4
4 x4
Обратный ход метода Гаусса
x1 1 x3 x4 2 x2
1 x3 x4 12 6 x3 8 x4
13 5 x3 7 x4
X (13 5 x3 7 x4 ; 6 3x3 4 x4 ; x3 ; x4 )
X b (13; 6;0;0)
8.
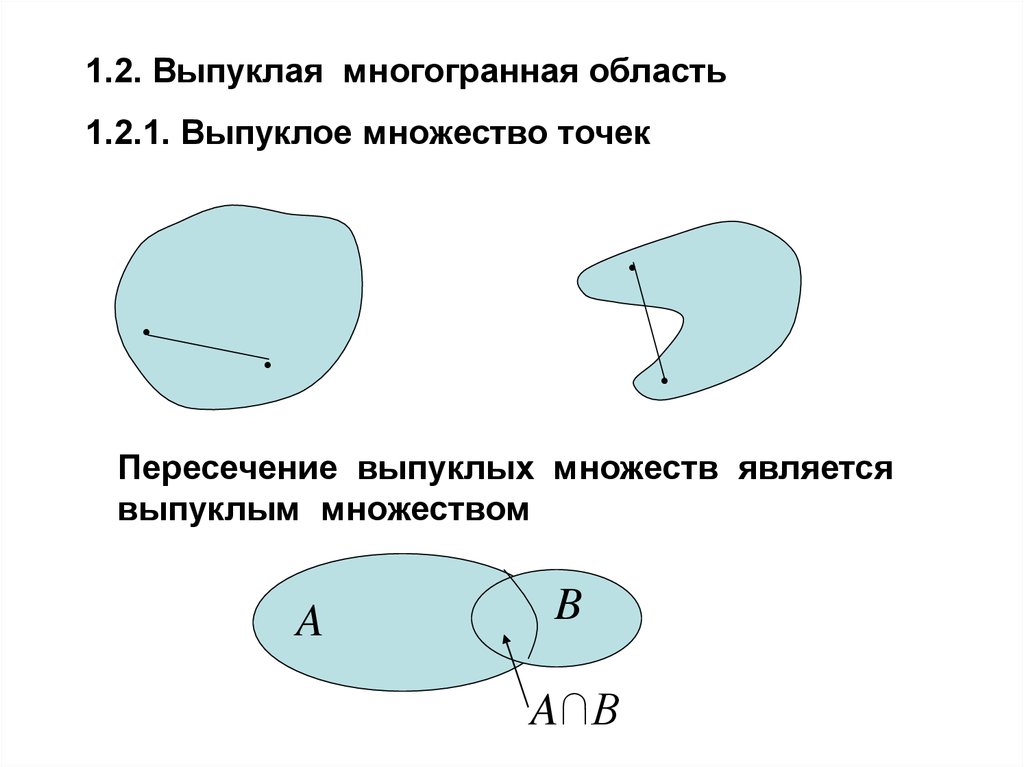
1.2. Выпуклая многогранная область1.2.1. Выпуклое множество точек
Пересечение выпуклых множеств является
выпуклым множеством
A
B
A∩B
9.
1.2.3. Гиперплоскость, полупространствоa1 x1 a2 x2 an xn b
a1 x1 a2 x2 an xn b
Примеры:
1.
n=2
2 x1 3x2 6
--
2 x1 3x2 6
-- полуплоскость
прямая
10.
2.n=3
2 x1 3x2 3x3 6
--
2 x1 3x2 3x3 6
-- полупространство
плоскость
x3
x2
x1
11.
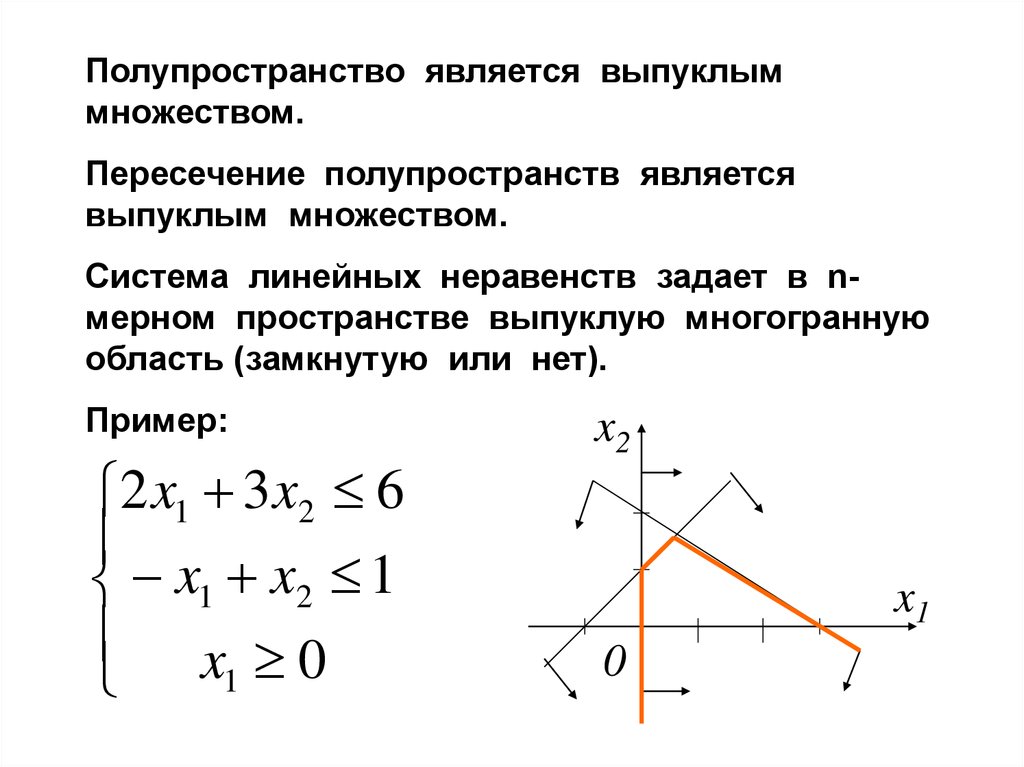
Полупространство является выпуклыммножеством.
Пересечение полупространств является
выпуклым множеством.
Система линейных неравенств задает в nмерном пространстве выпуклую многогранную
область (замкнутую или нет).
Пример:
2 x1 3 x2 6
x1 x2 1
x 0
1
x2
x1
0
12.
a11 x1 a12 x2 a1n xn b1a x a x a x b
21 1 22 2
2n n
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
am1 x1 am 2 x2 amn xn bm .
1.3. Крайние (опорные) точки множества
13.
2. Задач линейногопрограммирования (ЗЛП)
2.1. Примеры ЗЛП
2.1.1. Задача об использовании сырья
сырье
пр1
пр2
запасы
С1
2
3
19
С2
2
1
13
С3
0
3
15
С4
3
0
18
прибыль
7
5
14.
Пусть x1 и x2 -- планируемый выпуск продукцииПр1 и Пр2 соответственно. Тогда
2 x1 3 x2 19
2 x x 13
1 2
3 x2 15
3 x1
18
x1, 2 0.
F ( x) 7 x1 5 x2 max .
15.
2.1.2. Задача о диетеПитательные в-ва
норма
пр1
пр2
В1 -- белки
b1
a11
a12
В2 -- жиры
b2
a21
a22
В3 -- углеводы
b3
a31
a32
В4 -- витамины
b4
a41
a42
В5 -- вода
b5
a51
a52
c1
c2
Стоимость ед в-ва
16.
aij -- количество i-го питательного в-ва в 1 j-гопродукта
Пусть x1 и x2 -- планируемый рацион Пр1 и Пр2
соответственно. Тогда
a11 x1 a12 x2 b1
a x a x b
2
21 1 22 2
a31x1 a32 x2 b3
a41x1 a42 x2 b4
a51x1 a52 x2 b5
x1 , x2 0
F ( x) c1 x1 c2 x2 min .
17.
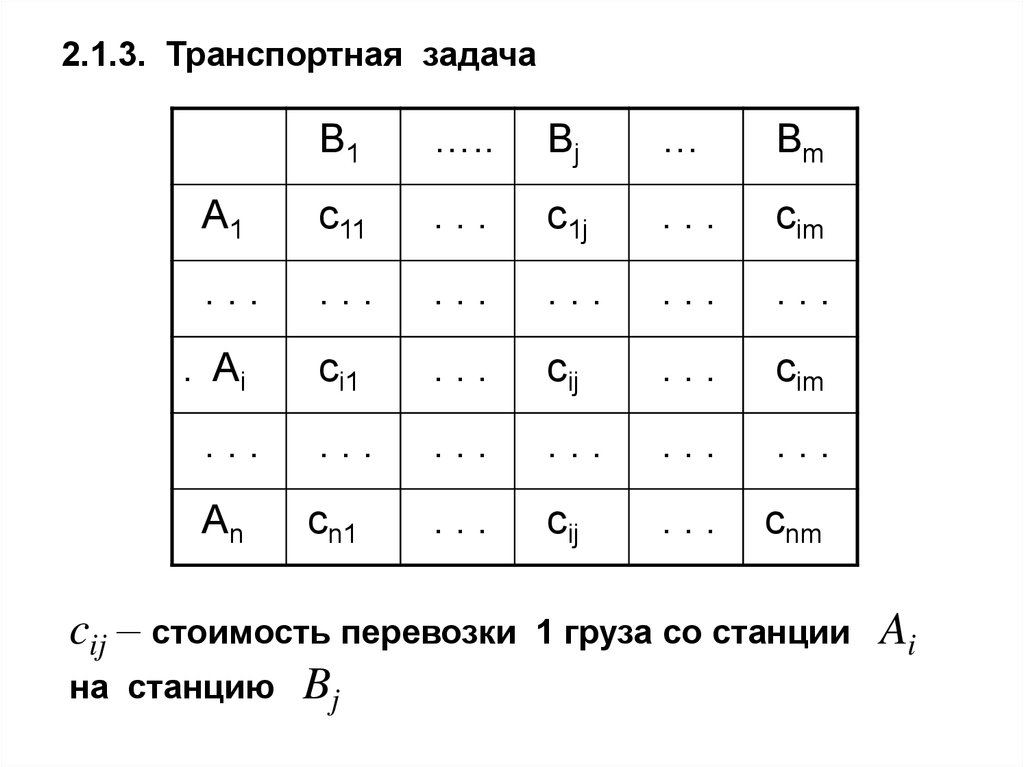
2.1.3. Транспортная задачаB1
…..
Bj
…
Bm
A1
c11
...
c1j
...
cim
...
...
...
...
...
...
ci1
...
cij
...
cim
...
...
...
...
...
...
An
cn1
...
cij
...
cnm
. Ai
cij – стоимость перевозки
на станцию Bj
1 груза со станции
Ai
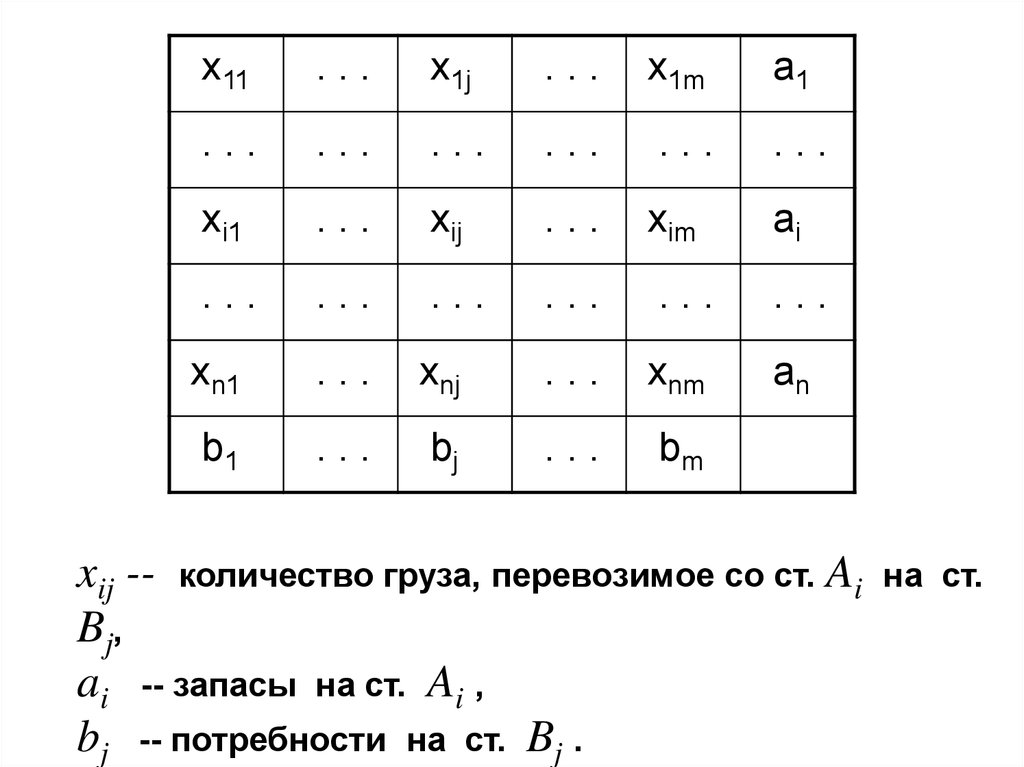
18.
x11...
x1j
...
x1m
a1
...
...
...
...
...
...
xi1
...
xij
...
xim
ai
...
...
...
...
...
...
xn1
...
xnj
...
xnm
an
b1
...
bj
...
bm
xij -- количество груза, перевозимое со ст. Ai
Bj,
ai -- запасы на ст. Ai ,
bj -- потребности на ст. Bj .
на ст.
19.
a bi
i
j
j
Все запасы должны быть вывезены, и все
потребности должны быть удовлетворены
x11 x1m a1
. . . . . . . . . . . .
xn1 xnm an
x11 xn1 b1
. . . . . . . . . . . .
x1m x nm b m
xij 0 i, j
20.
F ( x) cij xij mini, j
2.2. Виды ЗЛП
2.2.1. Общая ЗЛП (ОбЗЛП)
a11 x1 a1n xn b1
. . . . . . . . . . . .
ak1 x1 akn xn bk
a
x
a
x
b
k
11
1
k
1
n
n
k 1
. . . . . . . . . . . .
am1x1 amn x n b m
21.
xi 0F ( x) c0 ci xi opt
i
2.2.2. Основная ЗЛП (ОсЗЛП)
a11 x1 a1n xn b1
..............
am1 x1 amn xn bm
x 0
i
F ( x) c0 ci xi min
i
22.
2.2.3. Каноническая ЗЛП (КЗЛП)a11 x1 a1n xn b1
..............
am1 x1 amn xn bm
x 0
i
F ( x) c0 ci xi max
i
2.2.4. Переход от одного вида ЗЛП к другому
КЗЛП → ОсЗЛП
23.
0 b1 a11 x1 a1n xn xn 1..............
0 bm am1 x1 amn xn xn m
x 0, i 1, 2, , n m
i
F1 ( x) F ( x) c0 ci xi min
i
Опуская левые неравенства, получим систему
линейных уравнений
24.
Пример3 x1 4 x2 10
4 x1 x2 5
x2 2
xi 0, i 1,2.
F ( x) x1 2 x2 max
25.
0 10 3 x1 4 x2 x30 5 4 x1 x2 x4
0 2 x2 x5
xi 0, i 1,...,5
F ( x) x1 2 x2 min
Опуская левые неравенства, получим систему
линейных уравнений
26.
3 x1 4 x2 x3x4
4 x1 x2
x2
xi 0, i 1,...,5
10
5
x5 2
F ( x) x1 2 x2 min
ОсЗЛП → КЗЛП
27.
Пусть r – ранг матрицы системы уравненийп.2.2.2. и имеется решение системы ограничений
x1 1 1r 1 xr 1 1n xn 0
......................
x x x 0
r
rr 1 r 1
rn n
r
Опуская равенства слева, получим систему
линейных неравенств.
F1 ( x) F ( x) 0
n
x
i r 1
i i
max
28.
Примерx1 2 x2 3 x3 4 x4 10
2x1 - x 2 x 3 - 3x 4 -1
3x x 4 x x 9
3
4
1 2
xi 0, i 1,...,4.
F ( x) x1 x2 x3 x4 min
29.
1 2 3 4 102 1 1 3 1
3 1 4 1
9
3
4
10
1 2
0 5 5 11 21
0 5 5 11 21
1 2 3 4 10
11
21
0
1
1
5
5
30.
x1 2 x2 10 3 x3 4 x421
11
x
x
2
3
5
5 x4
x1 10 3x3 4 x4 425 2 x3 225 x4
x3 52 x4
8
5
F ( x) x3 52 x4 215
8
5
x3
11
5
x3 x4
29
5
x4 x3 x4
4
5
31.
5 x3 2 x4 85 x3 11x4 21
x3, 4 0.
F ( x)
29
5
x3 x4 max
4
5
32.
3. Геометрический смысл ЗЛПи геометрический способ ее
решения
Рассмотрим КЗЛП. Среди всех точек замкнутой
выпуклой многогранной области требуется найти
ту, в которой целевая функция принимает
максимальное значение. Решение находится
среди опорных точек области.
Пример:
Рассмотрим КЗЛП -- задачу об использовании
сырья
33.
2 x1 3 x2 192 x x 13
1 2
3 x2 15
3 x1
18
x1, 2 0.
F ( x) 7 x1 5 x2 max .
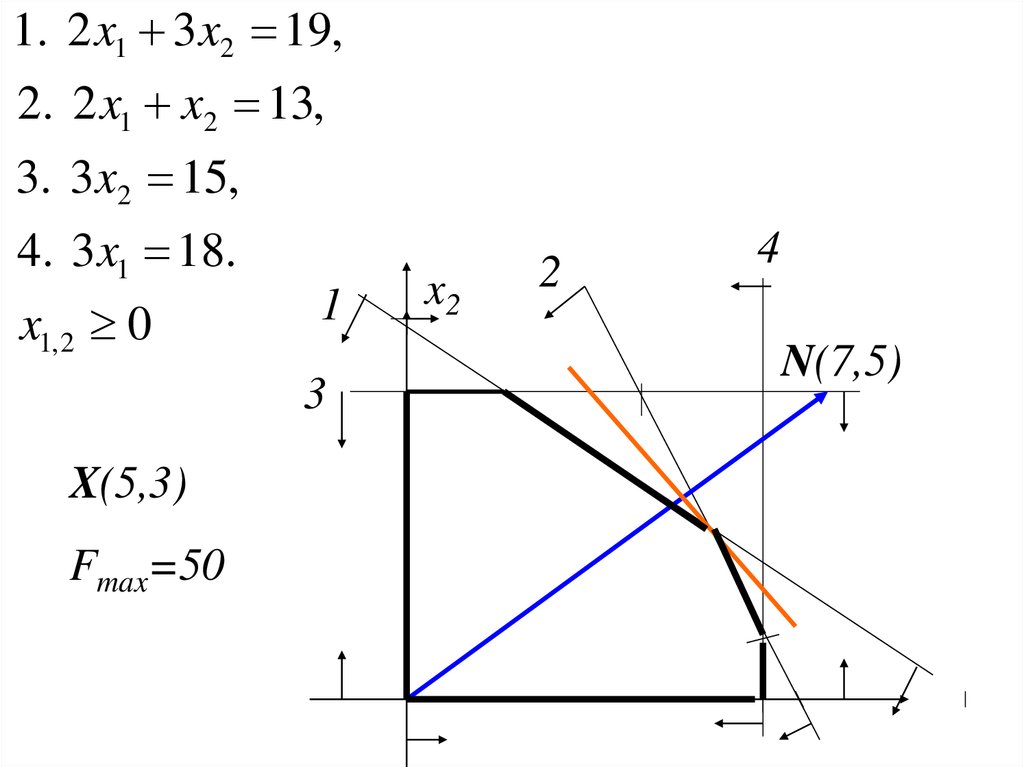
34.
1. 2 x1 3 x2 19,2. 2 x1 x2 13,
3. 3 x2 15,
4. 3 x1 18.
x1, 2 0
1
3
X(5,3)
Fmax=50
x2
2
4
N(7,5)
35.
4. Симплекс-метод4.1. Перебор базисных решений
Рассмотрим ОсЗЛП -- задачу об
использовании сырья.
x3 19 2 x1 3 x2
x 13 2 x x
4
1
2
x
15
3
x
5
2
x6 18 3 x1 ,
xi 0, i 1, ,6, F ( x) 7 x1 5 x2 min
X 1 (0,0,19,13,15,18); F1 0.
36.
Увеличиваяx1,
мы уменьшаем
F(x)
x3, x4 ,x6 при этом уменьшаются и раньше всех
обращается в нуль x6
x1 6 13 x6
x 7 3x 2 x
2
2
3 6
2
x
1
x
2
3 x6
4
x5 15 3x2
xi 0, i 1, ,6; F ( x) 42 5 x2 73 x6 min .
X 2 (6,0,7,1,15,0);
F2 42.
37.
Увеличиваяx2,
мы уменьшаем
F(x)
x3, x4 ,x5 при этом уменьшаются и раньше всех
обращается в нуль x4
x1 6 13 x6
x 1 x 2 x
2
4
3 6
4
x
4
3
x
4
3 x6
3
x5 12 3 x4 2 x6
xi 0, i 1, ,6; F ( x) 47 5 x4 x6 min .
X 3 (6,1,7,0,12,0);
F3 47.
38.
Увеличиваяx6,
мы уменьшаем
F(x)
x1, x3 ,x5 при этом уменьшаются и раньше всех
обращается в нуль x3
x1 5 14 x3 34 x4
1
1
x
3
x
2
2 3
2 x4
3
3
x
6
x
2 3
2 x4
5
x6 3 34 x3 94 x4
xi 0, i 1, ,6; F ( x) 50 34 x3 114 x4 min .
X 4 (5,3,0,0,6,3);
F4 50.
Решение оптимально.
39.
x2X4
X1
0
X3
X2
x1
40.
4.2. Алгоритм симплекс-метода4.2.1. Найти исходное допустимое базисное
решение
4.2.2. Выбрать свободную неизвестную, которая
входит в выражение для целевой функции со
знаком «--». Пусть это xi. Если таковой нет -решение оптимально.
4.2.3. Определить базисные неизвестные, которые
уменьшаются при увеличении xi, и выбрать ту,
которая раньше других обращается нуль. Пусть
это xj. Если таковых нет, задача оптимального
решения не имеет.
4.2.4. Поменять xi и xj ролями и выразить новый
набор базисных неизвестных через свободные
4.2.5. См. п. 4.2.2.
41.
4.3. Алгебра симплекс-метода.Симплекс-таблица
1. Записать исходное базисное решение и
целевую функцию в стандартном виде
x1 1 ( 1r 1 xr 1 1 j x j 1n xn )
.........................
xi i ( ir 1 xr 1 ij x j in xn )
.........................
x r r ( rr 1 xr 1 rj x j rn xn )
F ( x) 0 ( r 1 xr 1 j x j n xn )
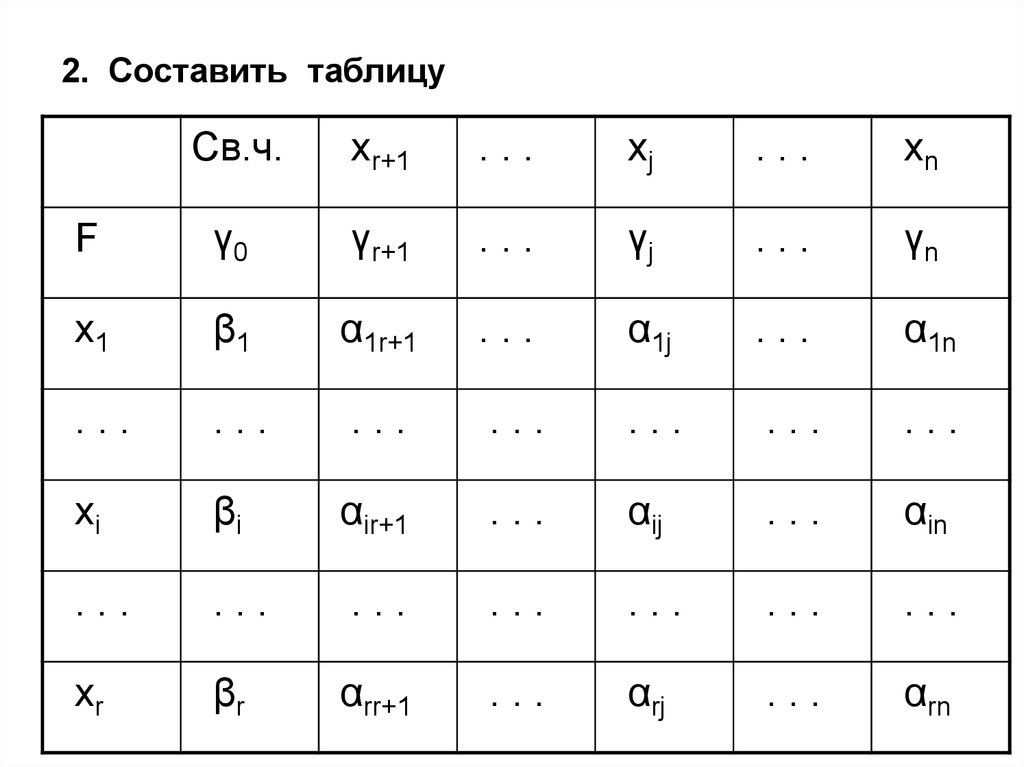
42.
2. Составить таблицуСв.ч.
xr+1
...
xj
...
xn
F
γ0
γr+1
...
γj
...
γn
x1
β1
α1r+1
...
α1j
...
α1n
...
...
...
...
...
...
...
xi
βi
αir+1
...
αij
...
αin
...
...
...
...
...
...
...
xr
βr
αrr+1
...
αrj
...
αrn
43.
Столбец xj называется генеральным столбцом,строка xi -- генеральной строкой,
элемент αij -- генеральным элементом
Правило выбора ген. ст-ца:
выбирается любой столбец, у которого в
первой строке положительное число (γj > 0)
Правило выбора генерального элемента:
из всех положительных чисел генерального
столбца ( не считая первой строки ) выбрать то,
для которого минимально отношение к нему
свободного члена ( αij > 0, βj/αij → min )
3. Выбрать генеральный столбец и генеральную
строку
4. Пересчитать симплекс-таблицу
44.
iij
ir 1
ij
i
kj ij
ir 1
ij
in
ij
x j (
xr 1 ij xi xn )
........................
x
(
x
k
k
kr
1
r
1
(
(
1
xr 1 ij xi
1
in
ij
xn ))
k ij kj i
kn xn )
ij
kr 1 ij kj ir 1
kn ij kj in
(
xr 1
xn ),
ij
ij
45.
F ( x) 0 ( r 1 xr 1i
i ij
(
(
ir 1
ij
xr 1 ij xi
1
in
ij
xn ))
n xn )
0 ij j i r 1 ij j ir 1
(
xr 1
ij
ij
j
n ij j in
xi
xn ).
ij
ij
46.
Правила пересчета симплекс-таблицы:• на месте генерального элемента пишется
величина, ему обратная
• все элементы генеральной строки (кроме
генерального эл-та) делятся на генеральный
элемент
• все элементы генерального столбца (кроме
генерального эл-та) делятся на генеральный
элемент и берутся с противоположным знаком
• все остальные элементы подсчитываются по
правилу прямоугольника:
0 ij j i
~
0 ij ,
~ ij i j
ij ,
ij j i
~
ij ,
~
ij i j
ij
47.
4.4. Порядок работы по симплекс-методу4.4.1. Найти исходное допустимое базисное
решение.
4.4.2. Записать найденное решение в стандартной
форме и составить симплекс-таблицу.
4.4.3. Выбрать генеральный столбец. Если
генеральный столбец выбрать нельзя, решение
оптимально.
4.4.4. Выбрать генеральную строку. Если
генеральную строку выбрать нельзя, задача
оптимального решения не имеет, т.к. целевая
функция не ограничена снизу.
4.4.5. Пересчитать симплекс-таблицу.
4.4.6. См. п. 4.4.3.
48.
Пример: Задача об использования сырьяx3 19 (2 x1 3 x2 )
x 13 (2 x x )
4
1
2
3 x2 )
x5 15 (
x 6 18 - (3x 1
)
F ( x ) (7 x1 5 x2 )
F
x3
x4
x5
x6
Св.ч.
0
19
13
15
18
x1
7
2
2
0
3
x2
5
3
1
3
0
49.
Св.ч.x6
x2
F
-42
-7/3
5
x3
7
-2/3
3
x4
1
-2/3
1
x5
15
0
3
x1
6
1/3
0
F
x3
x2
x5
x1
Св.ч.
-47
4
1
12
6
x6
1
4/3
-2/3
2
1/3
x4
-5
-3
1
-3
0
50.
Fx6
x2
x5
x1
Св.ч.
-50
3
3
6
5
x3
-3/4
3/4
1/2
-3/2
-1/4
x4
-11/4
-9/4
X (5,3,0,0,6,3),
Fmin 50.
4.5. Теорема. При решении ОсЗЛП симплексметодом за конечное число шагов мы приходим
либо к оптимальному решению, либо к выводу, что
задача оптимального решения не имеет, т.к. целевая
функция не ограничена снизу.
51.
5. М-метод(метод искусственного базиса)
Пусть имеется ОсЗЛП
Am n X n 1 Bm 1 , x j 0, j 1, , n,
F ( x) c0 c j x j min .
j
Рассмотрим систему уравнений
a11 x1 a1n xn b1
..............
a x a x b
mn n
m
m1 1
Можно считать, что все правые части
неотрицательны
52.
Введем новые переменные1 b1 (a11 x1 a1n xn )
..................
b (a x a x )
m
m1 1
mn n
m
И рассмотрим следующую ОсЗЛП
m 1 Bm 1 Am n X n 1 , bi 0, i 1, , m
i 0, i 1, , m, x j 0, j 1, , n
m
G ( x) F ( x) M i min
i 1
M
-- достаточно большое положительное число
53.
Построенная задача называетсяM—задачей.
5.1. Основные теоремы
Теорема 1. Если M—задача имеет оптимальное
решение, в котором все ξi перешли в свободные
неизвестные или обратились в нуль, то исходная
задача имеет оптимальное решение и при этом
Fmin=Gmin
Теорема 2. Если M—задача имеет оптимальное
решение, в котором хотя бы одна переменная ξi
осталась в числе базисных неизвестных и не
обратилась в нуль, то исходная задача
противоречива.
54.
Теорема 3. Если M—задача оптимального решенияне имеет, то исходная задача также оптимального
решения не имеет. (не обязательно целевая
функция не ограничена снизу).
5.2 Примеры:
1.
3x1 x2 x3 x4 2 x5 10
6 x1 x2 2 x3 3x4 4 x5 20
10 x x 3x 6 x 7 x 30
3
4
5
1 2
x j 0,
j 1, ,5
F ( x) x1 x2 x3 x4 2 x5 max .
55.
СоставимM--задачу
1 10 (3 x1 x2 x3 x4 2 x5 )
2 20 (6 x1 x2 2 x3 3 x4 4 x5 )
30 (10 x x 3 x 6 x 7 x )
1
2
3
4
5
3
x j 0, j 1, ,5
G ( x) 60 M [(1 19 M ) x1 (1 3M ) x2
( 1 6 M ) x3 (1 10 M ) x4 (2 13M ) x5 ] min
Симплекс-таблица:
56.
↑←
x2
x3
x4
x5
F
Св.ч x1
.
0
1
1
-1
1
-2
M
60
19
3
6
10
-13
ξ1
10
3
1
1
1
-2
ξ2
20
6
1
2
3
-4
ξ3
30
10
1
3
6
-7
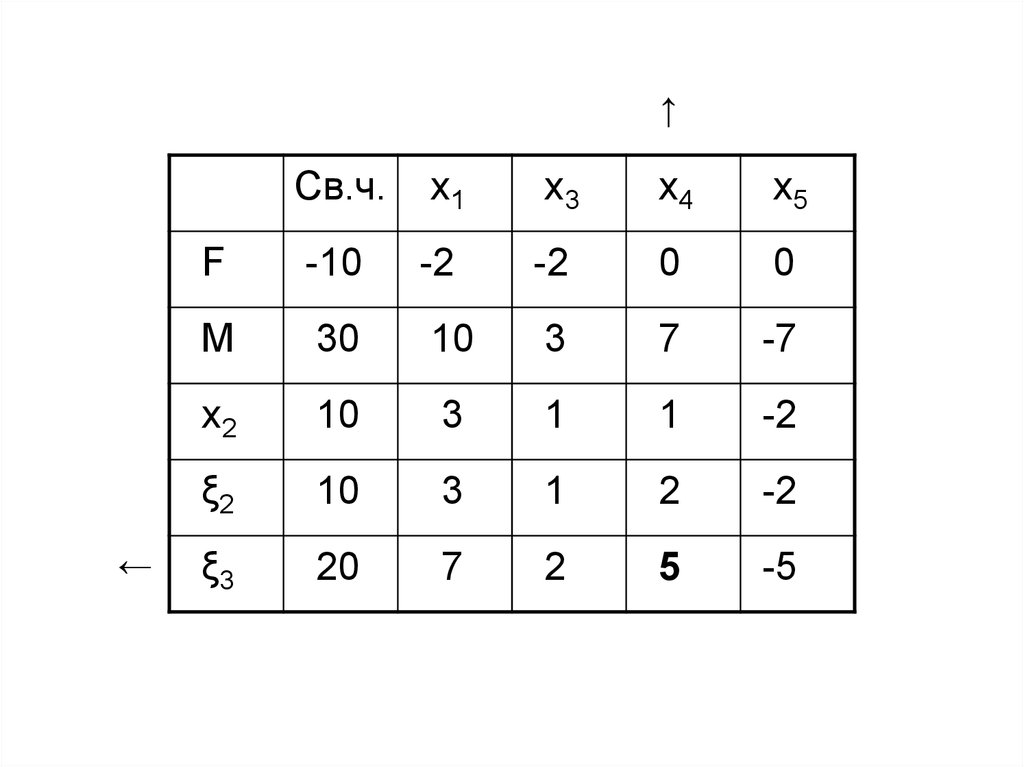
57.
↑←
Св.ч.
x1
x3
x4
x5
F
-10
-2
-2
0
0
M
30
10
3
7
-7
x2
10
3
1
1
-2
ξ2
10
3
1
2
-2
ξ3
20
7
2
5
-5
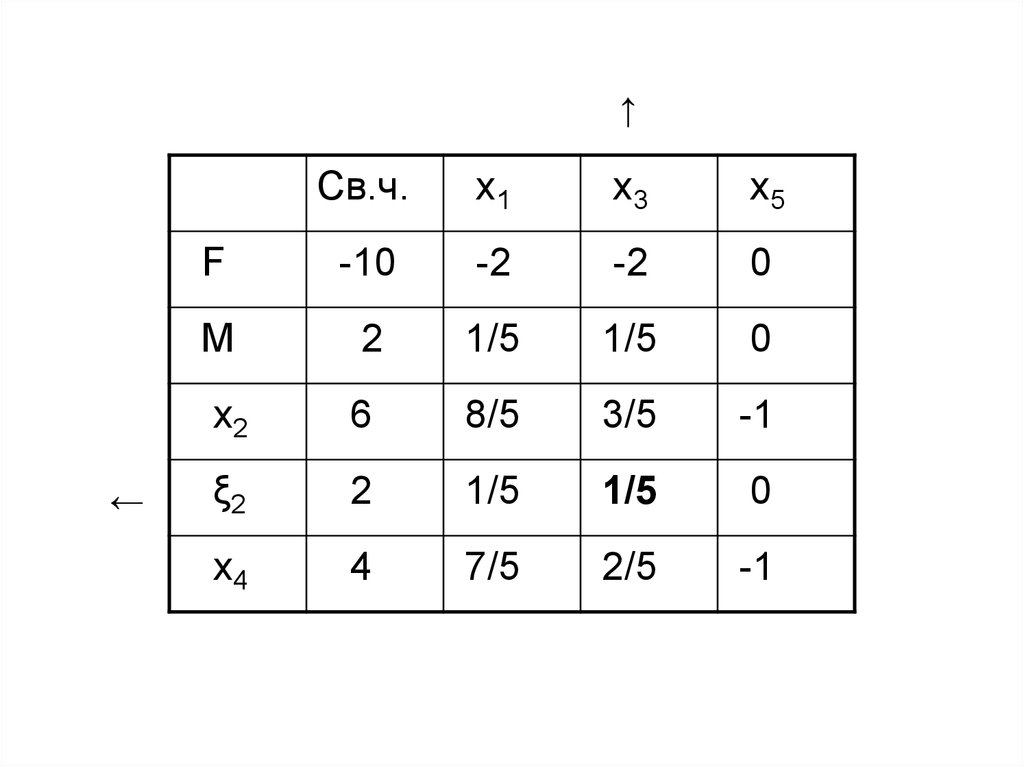
58.
↑←
Св.ч.
x1
x3
x5
F
-10
-2
-2
0
M
2
1/5
1/5
0
x2
6
8/5
3/5
-1
ξ2
2
1/5
1/5
0
x4
4
7/5
2/5
-1
59.
св.ч.x1
x5
F
10
0
0
x2
0
x3
10
x4
0
1
X M (0,0,10,0,0,0,0,0),
X (0,0,10,0,0),
Gmin 10,
Fmin 10.
60.
2.x1 2 x2 x3 x4 1
x1 2 x2 3x3 x4 2
x 5x x x 5
2
3
4
1
x j 0, j 1, ,4,
F ( x) x1 10 x2 x3 2 x4 max .
Составим M—задачу и симплекс-таблицу
61.
1 1 ( x1 2 x2 x3 x4 )2 2 ( x1 2 x2 3 x3 x4 )
5 ( x 5x x x )
1
2
3
4
3
x j 0, j 1, ,4, i 0, i 1,2,3,
G ( x) 8M [(1 M ) x1 (10 9M ) x2
( 1 3M ) x3 (2 M ) x4 ] min .
62.
FM
ξ1
ξ2
ξ3
С.ч.
x1
x2
x3
x4
0
8
1
2
5
1
1
1
-1
1
10
9
2
2
5
-1
3
-1
3
1
-2
-1
-1
1
1
↓
←
→
↑
С.ч.
x1
x3
x4
F
-5
-4
4
3
M
7/2
-7/2
15/2 7/2
x2
1/2
1/2
-1/2
-1/2
ξ2
1
-2
4
2
ξ3
5/2
-3/2
7/2
3/2
63.
FM
x2
x3
ξ3
Си.ч.
-6
13/8
5/8
1/4
13/8
x1
-2
1/4
1/4
-1/2
1/4
x4
1
-1/4
-1/4
½
-1/4
↓
Исходная задача
противоречива
F
M
x1
x3
ξ3
→
Св.ч.
-1
1
5/2
3/2
1
x2
8
-1
4
2
-1
x4
-1
0
-1
0
0
64.
3.x1 x2 x3 x4 0
x1 14 x2 10 x3 10 x4 11
x j 0, j 1,2,3,4,
F ( x) x1 4 x2 3 x3 10 x4 max .
M-задача
1 ( x1 x2 x3 x4 )
11 ( x1 14 x2 10 x3 10 x4 )
x j 0, j 1,2,3,4, i 0, i 1,2,
G 11M [(1 2 M ) x1 ( 4 15M ) x2
(3 9 M ) x3 (10 9 M ) x4 ] min .
65.
С.ч.x1
x2
x3
x4
F
0
1
-4
3
10
M
1
2
15
9
-9
ξ1
0
1
1
-1
1
ξ2
11
1
14
10 -10
→
↑
↓
c.ч.
Задача решений не
имеет, т.к. целевая
функция не
ограничена сверху
x1
x2
x4
F
-3,9 0,7
-8,2 13
M
1,1
1,1
2,4
0
ξ1
1,1
1,1
2,4
0
x3
1,1
1,1
1,4
-1
66.
6. Теория двойственности2 x1 3 x2 19
2 x x 13
1
2
3 x2 15
3 x1
18
x j 0, j 1,2,
F ( x) 7 x1 5 x2 max .
x j планируемое кол во изготовленной
продукции
67.
yi , i 1,2,3,4, продажная стоимостьединицы i - го сырья
3 y4 7
2 y1 2 y2
5
3y1 y 2 3y 3
yi 0, i 1,2,3,4,
F ( y ) 19 y1 13 y2 15 y3 18 y4 min .
68.
6.1. Задача, двойственная к КЗЛППо определению
1. Каждой переменной исходной задачи
соответствует ограничение двойственной задачи
2. Каждому ограничению исходной задачи
соответствует переменная двойственной задачи
3. Матрицы из коэффициентов двух задач
получаются друг из друга транспонированием
4. Все ограничения имеют вид неравенств «≥»
5. Переменные двойственной задачи должны
быть неотрицательными
6.Правые части системы ограничений
двойственной задачи совпадают с
коэффициентами при неизвестных в целевой
функции исходной задачи
69.
7. Коэффициенты при неизвестных в целевойфункции двойственной задачи совпадают с
правыми частями системы ограничений исходной
задачи
8. Свободные члены в целевых функциях двух
задач совпадают
9. Целевая функция двойственной задачи
минимизируется
Задача, двойственная к двойственной совпадает
с исходной
a11x1 a1n xn
Am n X n 1 . . . . . . . . . . .
am1 x1 amn xn
70.
ИсходнаяКЗЛП
Am n X n 1 Bm 1
xj 0
F ( x) c0 c j x j max
j
Двойственная
задача
AnT mYm 1 Cn 1
yi 0
F ( y ) c0 bi yi min
i
Двойственная
КЗЛП
AnT mYm 1 Cn 1
yi 0
F ( y ) c0 bi yi max
i
71.
Двойственная кдвойственной
КЗЛП
AmTT n Z n 1 Bm 1
zj 0
F ( z ) c0 c j z j min
j
Am n X n 1 Bm 1
xj 0
F ( x) c0 c j x j max
i
72.
6.2. Задача, двойственная к ОбЗЛП1. Все ограничения-неравенства согласованы со
способом оптимизации целевой функции, а
именно, если целевая функция минимизируется,
то все знаки неравенства имеют вид «≥» и
наоборот
2. Каждой переменной исходной задачи
соответствует ограничение двойственной задачи
3. Каждому ограничению исходной задачи
соответствует переменная двойственной задачи
4. Матрицы из коэффициентов двух задач
получаются друг из друга транспонированием
5. Переменные двойственной задачи,
соответствующие неравенствам в исходной
задаче должны быть неотрицательными
73.
6. Ограничения, соответствующие неотрицательнымпеременным исходной задачи должны иметь вид
неравенств противоположного смысла по сравнению
с неравенствами исходной задачи
7.
Правые части системы ограничений двойственной
задачи совпадают с коэффициентами при
неизвестных в целевой функции исходной задачи
8. Коэффициенты при неизвестных в целевой
функции двойственной задачи совпадают с
правыми частями системы ограничений исходной
задачи
9. Свободные члены в целевых функциях двух
задач совпадают
10. Целевая функция двойственной задачи
оптимизируется в противоположном смысле
74.
Пример:x1 2 x2 x3 3x4 x5 2
2 x1 x2 x3 2 x4 x5 3
x 3x x 4 x 2 x 1
2
3
4
5
1
x1,3,5 0
F ( x) 1 x1 x2 x3 2 x4 x5 min .
x1 2 x2 x3 3x4 x5 2
2 x1 x2 x3 2 x4 x5 3
x 3x x 4 x 2 x 1
2
3
4
5
1
x1,3,5 0
F ( x) 1 x1 x2 x3 2 x4 x5 min .
75.
y1 2 y2 y3 12 y y 3 y 1
1
2
3
y1 y2 y3 1
3y 2 y 4 y 2
2
3
1
y1 y2 3 y3 1
y2,3 0
F ( y ) 1 2 y1 3 y2 y3 max .
76.
6.3. Теоремы теории двойственности1. Первая теорема двойственности
opt
Fopt F
2. Основное неравенство теории двойственности
Если, например,
допустимых
x
и
F(x) → min,
y
F ( x) F ( y )
то для всех
77.
a11 y1 am1 ym c1. . . . . . . . . . . . . . .
a y a y c
mn m
n
1n 1
a11 x1 a1n xn b1
..............
a x a x b
mn n
m
m1 1
x j 0 j
yi любого знака
(ai1 x1 ain xn ) yi bi yi ,
(a1 j y1 amj ym ) x j c j x j
a x y b y ,
ij
i
i
i
j
i
i
a
ij
j
j
yi x j c j x j ,
i
j
b y a x y a
i
i
i
ij
i
j
F ( y ) F ( x).
j
i
ij
j
i
yi x j c j x j
j
78.
3. Вторая теорема двойственностиПусть имеются два допустимых решения двух
взаимно двойственных задач. Для того, чтобы
эти решения были оптимальными, необходимо и
достаточно выполнения следующих условий:
1. Если в каком-либо ограничении одной из задач
не достиглось строгое равенство, то
соответствующая переменная другой задачи
должна обратиться в нуль.
2. Если какая-либо переменная одной из задач
отлична от нуля, то в соответствующем
ограничении другой задачи должно достигаться
строгое равенство
79.
6.3. Решение двух взаимно двойственных задач1.
1
x1 x2 x3 x4
x1 2 x2 x3 3x4 x5 x6 1
x j 0, j 1, ,6,
F ( x) x1 5 x2 x3 10 x4 x5 3x6 min .
Составить двойственную задачу, решить ее и
Восстановить решение исходной задачи
80.
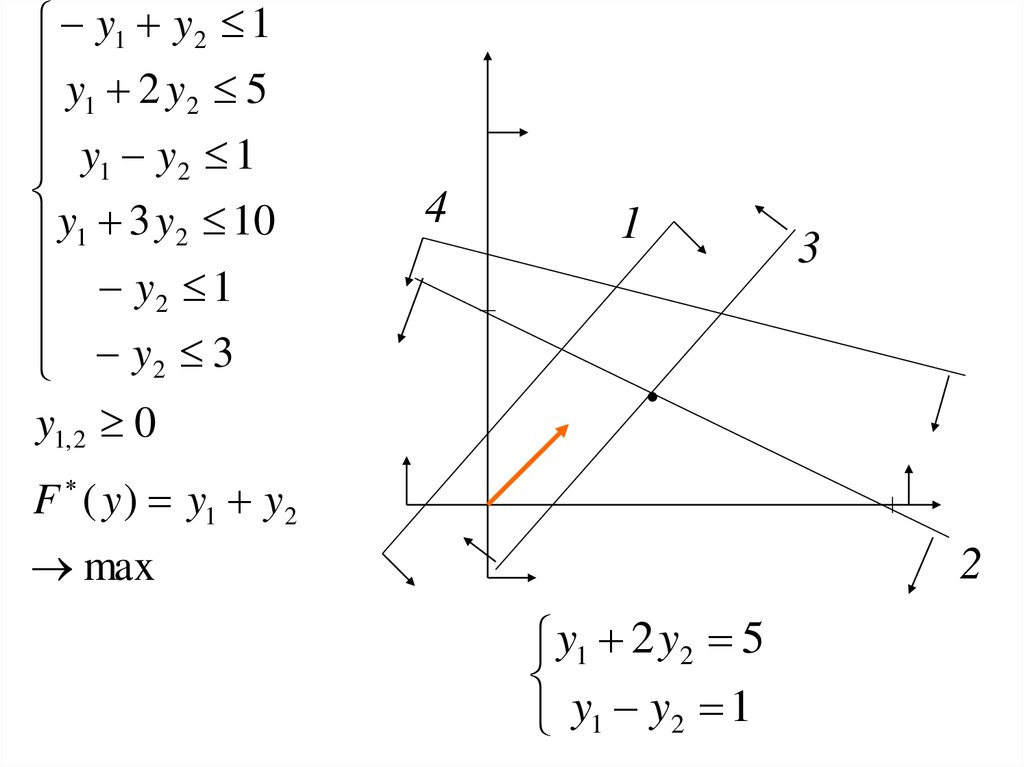
y1 y2 1y 2y 5
2
1
y1 y2 1
y1 3 y2 10
y2 1
y2 3
y1, 2 0
4
1
3
F ( y ) y1 y2
max
2
y1 2 y2 5
y1 y2 1
81.
73
4
3
Y ( , ),
max
F
113
x1 x4 x5 x6 0
x2 x3 1
2 x2 x3 1
2
1
x2 3 , x3 3 .
X (0, 23 , 13 ,0,0,0), Fmin 113 .
82.
2. Двойственный симплекс-методx1 2 x2 3x3 1
2 x1 x2 x 3 1
x1, 2,3 0,
F ( x) x1 2 x2 3x3 max
x4 1 ( x1 2 x2 3 x3 )
x5 1 (2 x1 x2 x3 )
F ( x) ( x1 2 x2 3 x3 )
y1 2 y2 1
2 y1 y2 2
3 y y 3
1
2
y1, 2 0,
F ( y ) y1 y2 min .
y3 1 ( y1 2 y2 )
y4 2 ( 2 y1 y2 )
y 3 (3 y y )
1
2
5
F ( y ) ( y1 y2 ).
83.
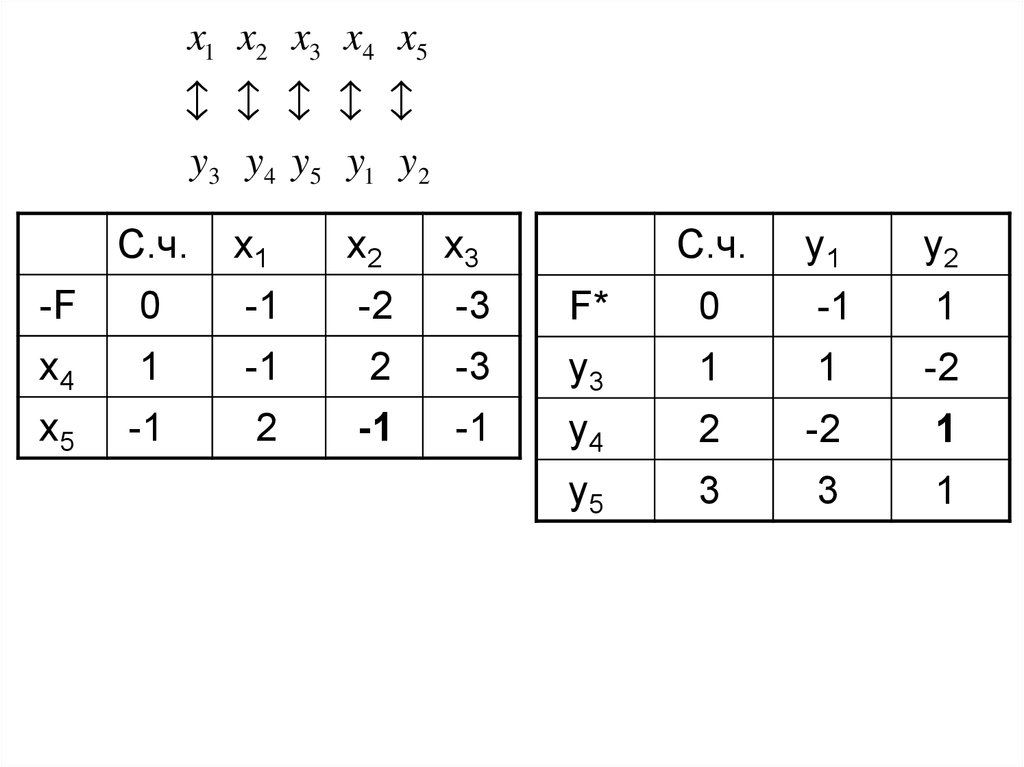
x1 x2 x3 x4 x5y3 y4 y5 y1 y2
С.ч.
x1
x2
x3
С.ч.
y1
y2
-F
0
-1
-2
-3
F*
0
-1
1
x4
1
-1
2
-3
y3
1
1
-2
x5
-1
2
-1
-1
y4
2
-2
1
y5
3
3
1
84.
С.ч.x1
x5
x3
-F
2
-5
-2
-1
x4
-1
3
2
x2
1
-2
-1
С.ч.
x1
x5
С.ч.
y1
y2
F*
-2
1
-1
-5
y3
5
-3
2
1
y4
2
-2
1
y5
1
5
1
x4
-F 11/5 -28/5 -12/5 -1/5
x3
1/5
-2/5
-2/5
-1/5
x2
4/5
-7/5
-3/5
1/5
F*
y3
y2
y1
С.ч.
-11/5
28/5
12/5
1/5
y5
-1/5
3/5
2/5
1/5
y4
-1/5
7/5
3/5
-1/5
X (0, 54 , 15 ,0,0), Fmax 115 ; Y ( 15 , 125 , 285 ,0,0), Fmin 115 .
85.
3. Двойственный М-методx1 2 x2 3 x3 1
2 x 3x x 1
2
3
1
3 x1 x2 2 x3 1
6 x 6 x 6 x 1
2
3
1
2 x1
4 x3 1
F ( x) 3 x1 5 x2 4 x3 min .
86.
y1 2 y2 3 y3 6 y4 2 y5 35
2 y1 3 y2 y3 6 y4
3y y 2y 6y 4y 4
2
3
4
5
1
yi 0, i 1, ,5,
F ( y ) y1 y2 y3 y4 y5 max .
x1 x2 x3 1 2 3 4 5
1 2 3 y1 y2 y3 y4 y5
87.
1 3 ( y1 2 y2 3 y3 6 y4 2 y5 ))
2 5 (2 y1 3 y2 y3 6 y4
4 (3y y 2y 6y 4y )
1
2
3
4
5
3
G 12 M [(6 M 1) y1 (6 M 1) y2 (8M 1) y3
(18M 1) y4 (6 M 1) y5 ] min .
-F*
M
ξ1
ξ2
ξ3
Св.ч.
0
12
3
5
4
y1
1
6
1
2
3
y2
1
6
2
3
1
y3
1
6
3
1
2
y4
1
18
6
6
6
y5
1
6
2
0
4
88.
-F*M
y4
ξ2
ξ3
Св.ч.
-3/6
3
5/6
2
1
y1
5/6
3
1/6
1
2
y2
4/6
0
2/6
1
-1
y3
3/6
-3
3/6
-2
-1
ξ1
-1/6
-3
1/6
-1
-1
y5
4/6
0
2/6
-2
2
Св.ч.
ξ3
y2
y3
ξ1
y5
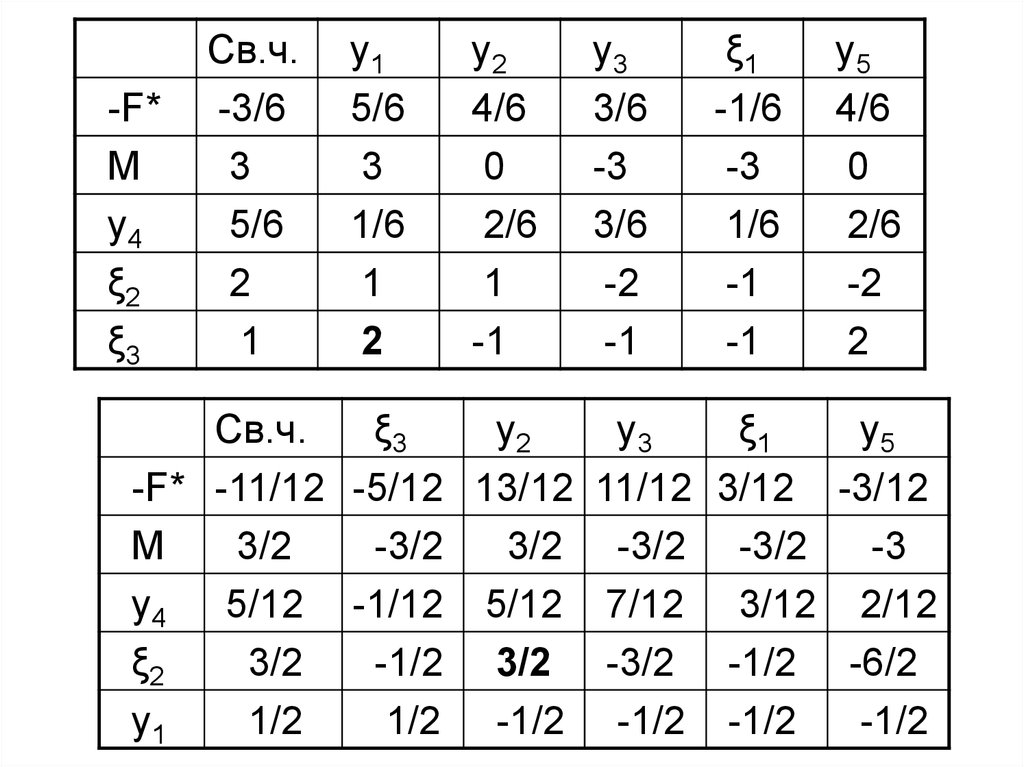
-F* -11/12 -5/12 13/12 11/12 3/12 -3/12
M
3/2
-3/2
3/2 -3/2 -3/2
-3
y4 5/12 -1/12 5/12 7/12 3/12 2/12
ξ2
3/2
-1/2 3/2 -3/2 -1/2 -6/2
y1
1/2
1/2 -1/2 -1/2 -1/2
-1/2
89.
-F*M
y4
y2
y1
c.ч. ξ3
ξ2
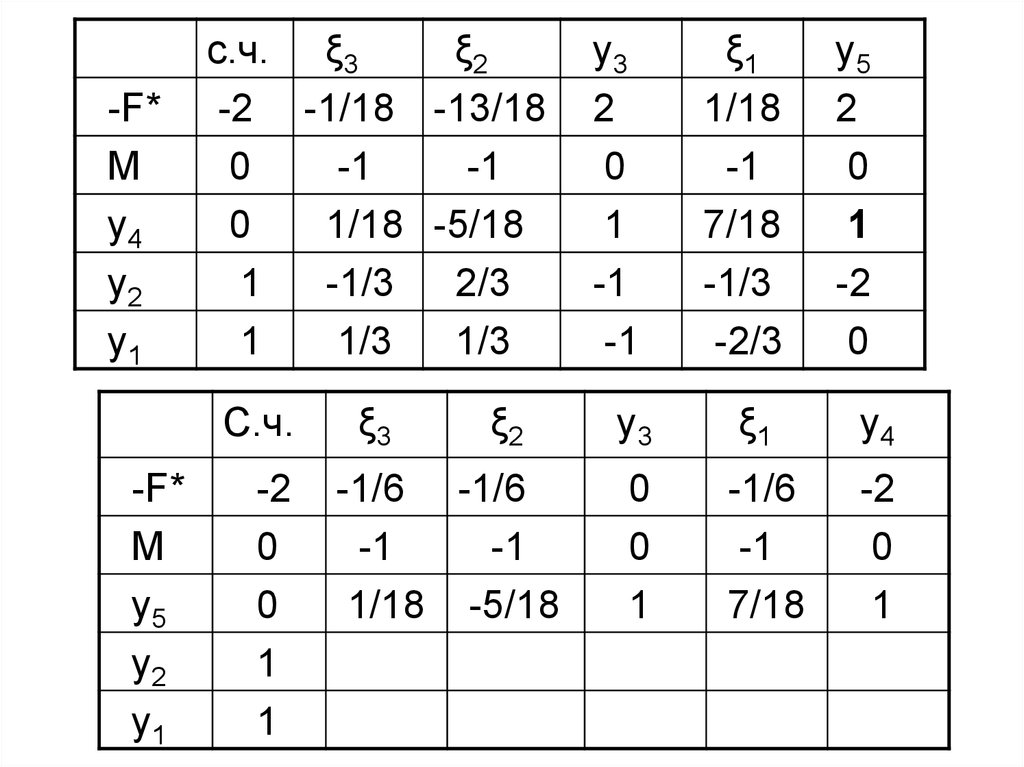
-2 -1/18 -13/18
0
-1
-1
0
1/18 -5/18
1
-1/3
2/3
1
1/3
1/3
С.ч.
-F*
M
y5
y2
y1
-2
0
0
1
1
ξ3
ξ2
-1/6 -1/6
-1
-1
1/18 -5/18
y3
2
0
1
-1
-1
ξ1
1/18
-1
7/18
-1/3
-2/3
y5
2
0
1
-2
0
y3
ξ1
y4
0
0
1
-1/6
-1
7/18
-2
0
1
90.
1 , 2 , 3 , y1 , y2 , y3 y4 , y5Y (0,0,0,1,1,0,0,0),
max
F
2.
X ( , , ,0,0,0,2,0), Fmin 2.
1
6
1
6
1
6
x1 , x2 , x3 , 1 , 2 , 3 , 4 , 5



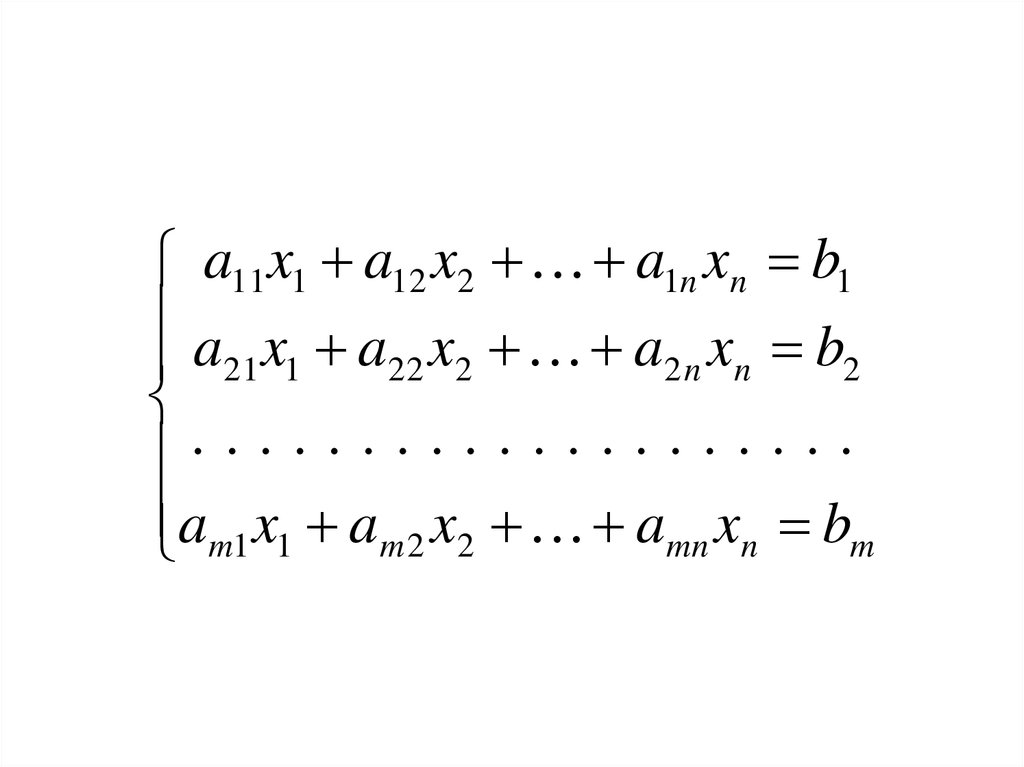















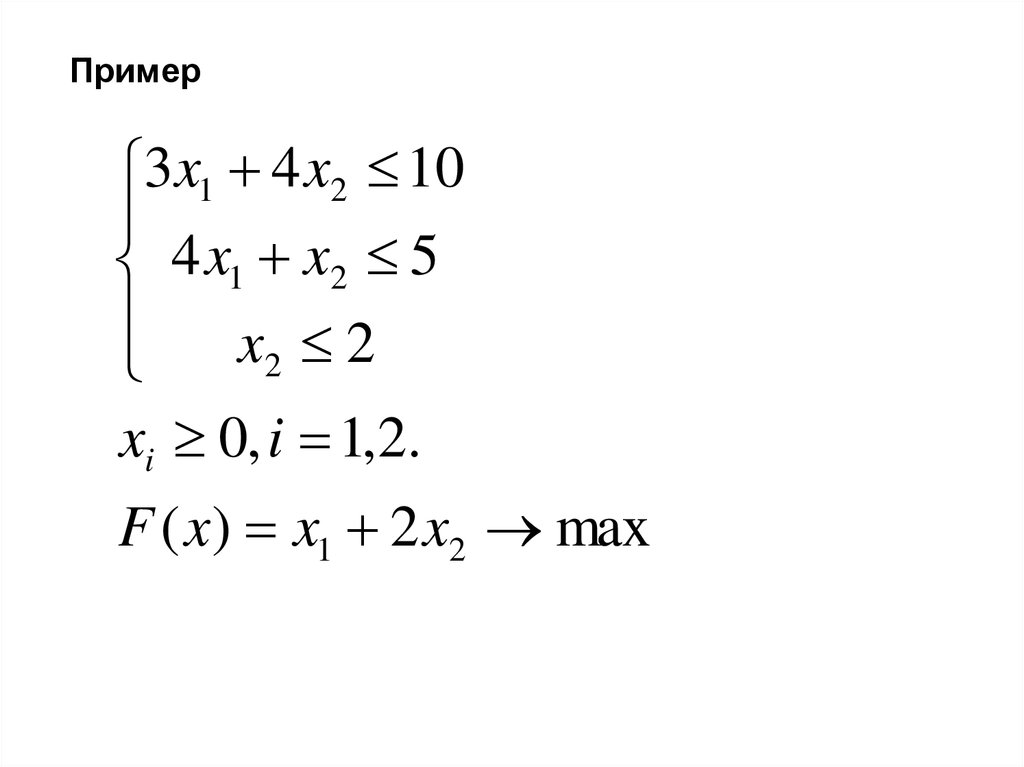






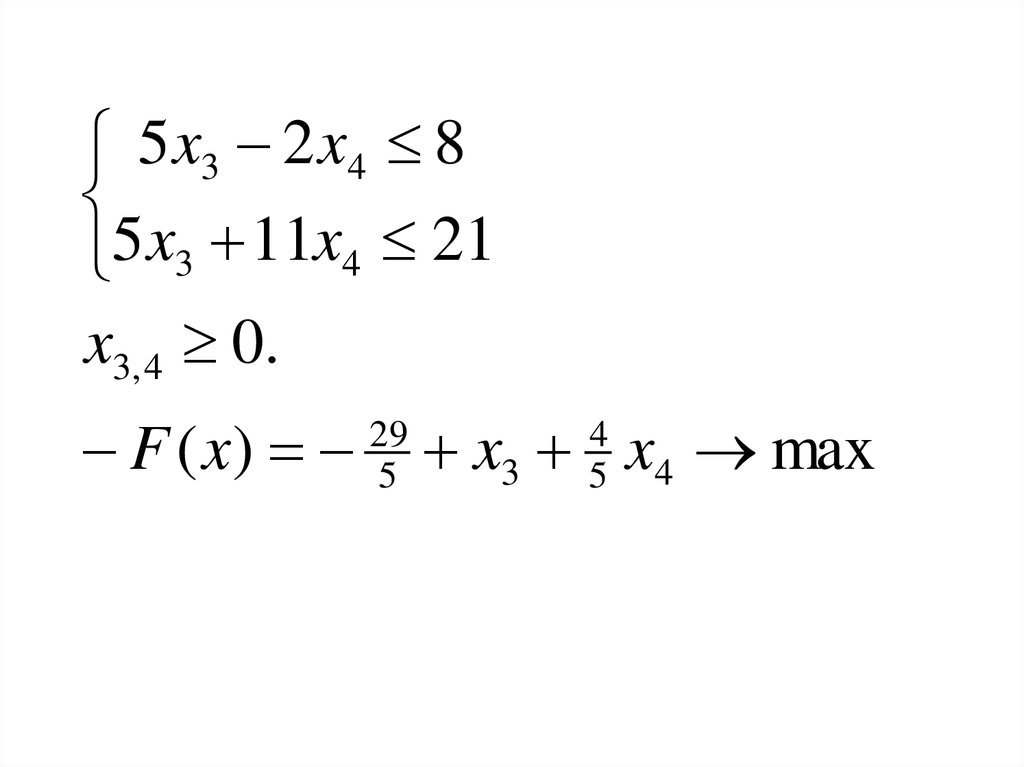

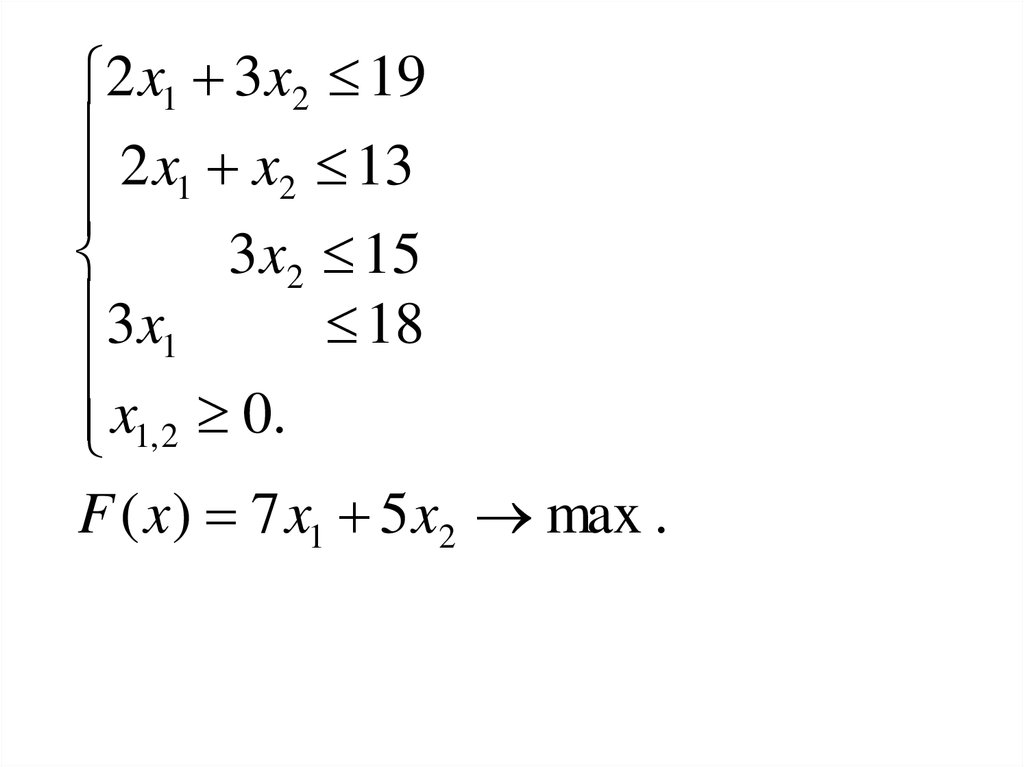








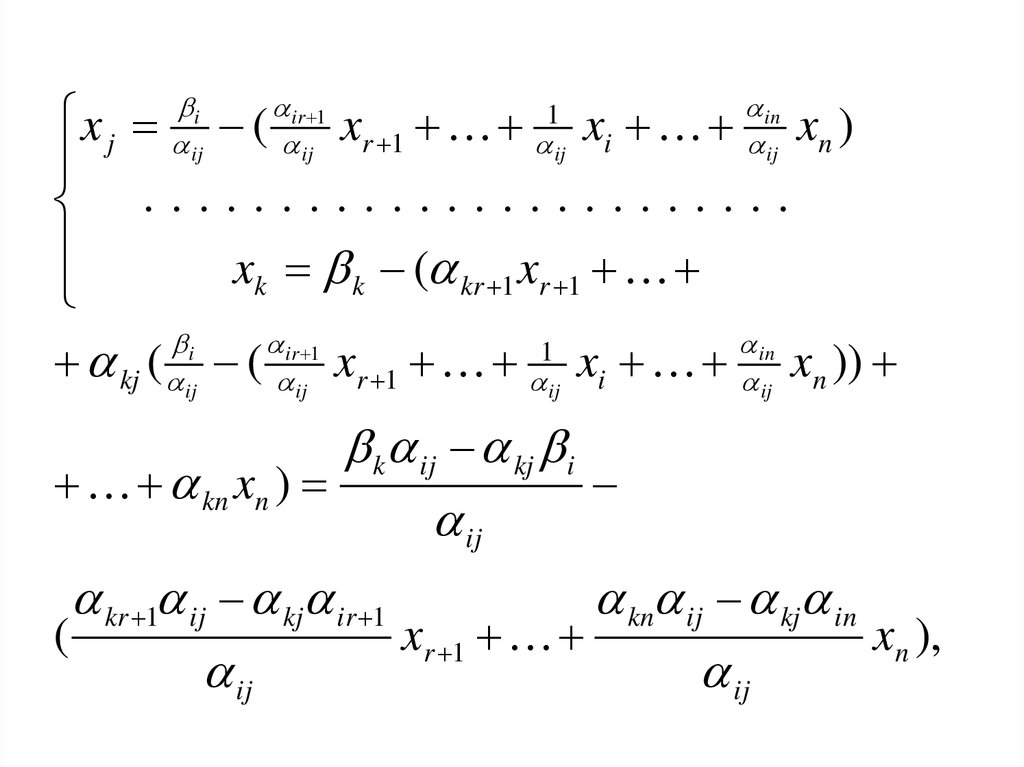
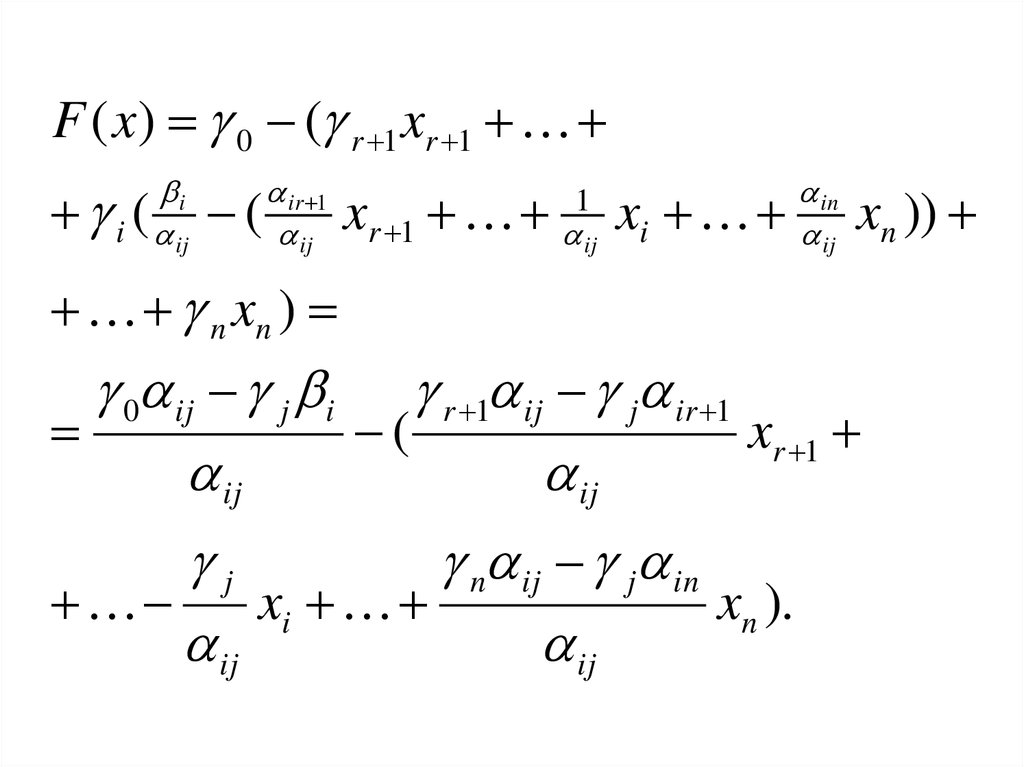
















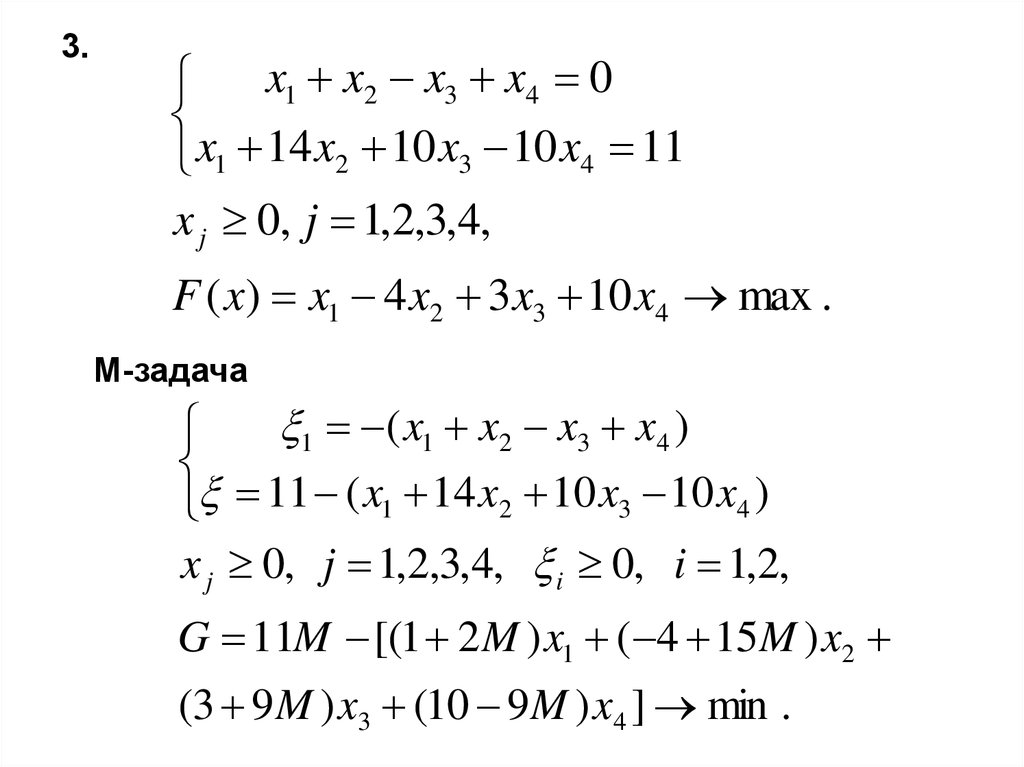









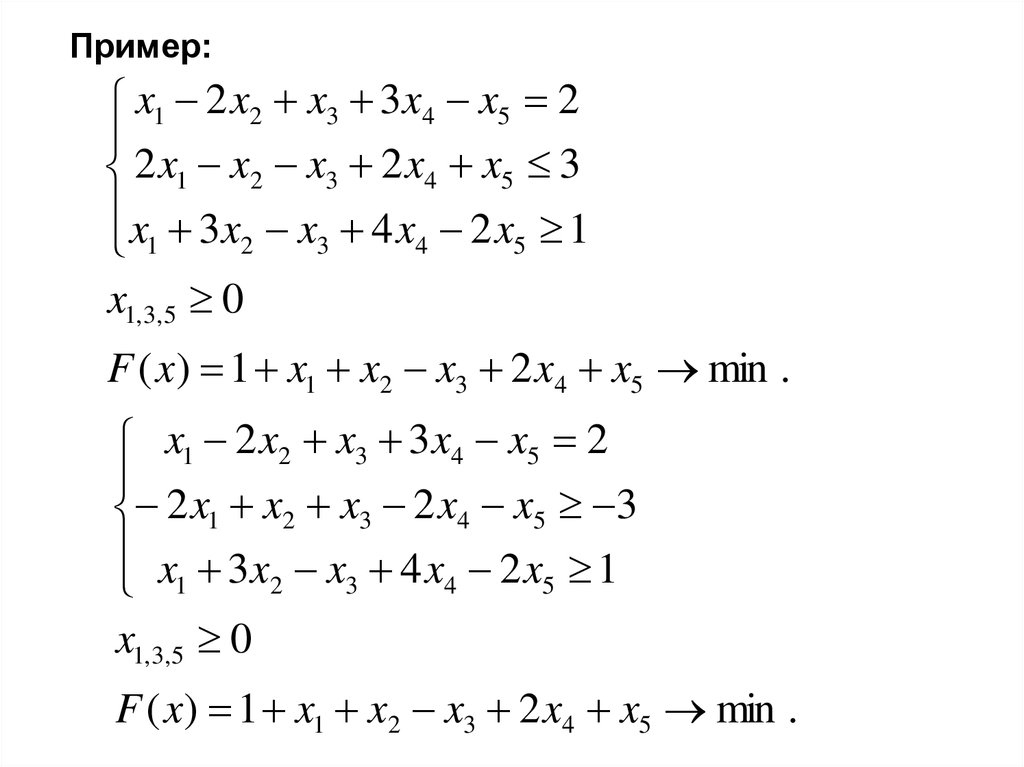


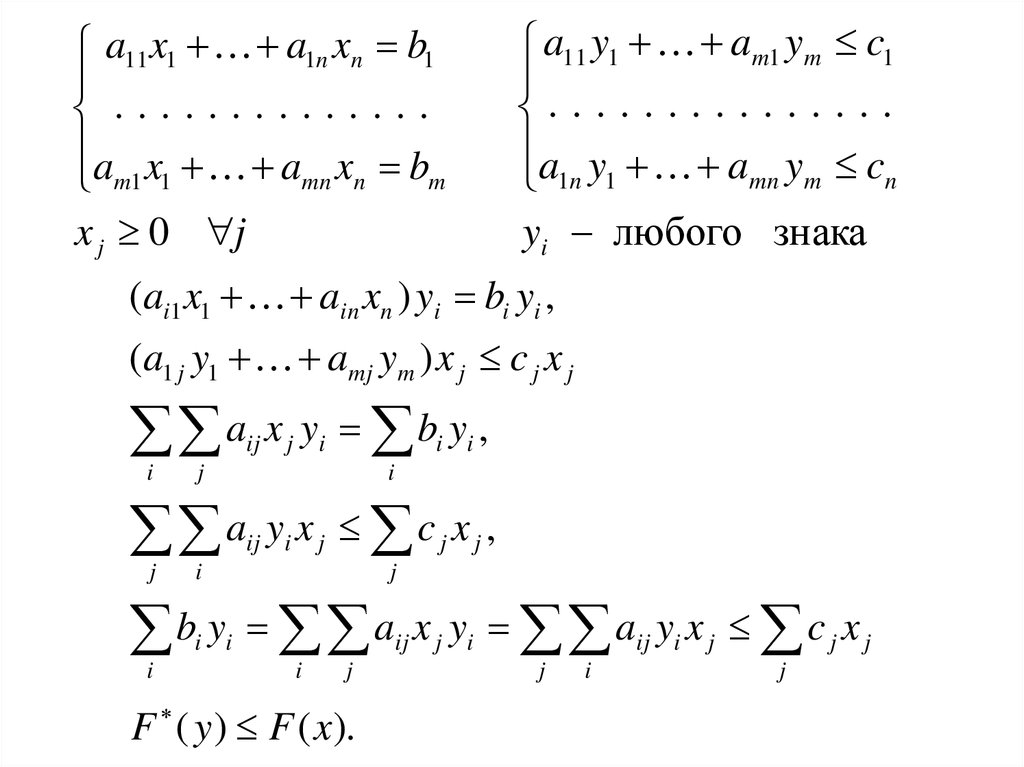


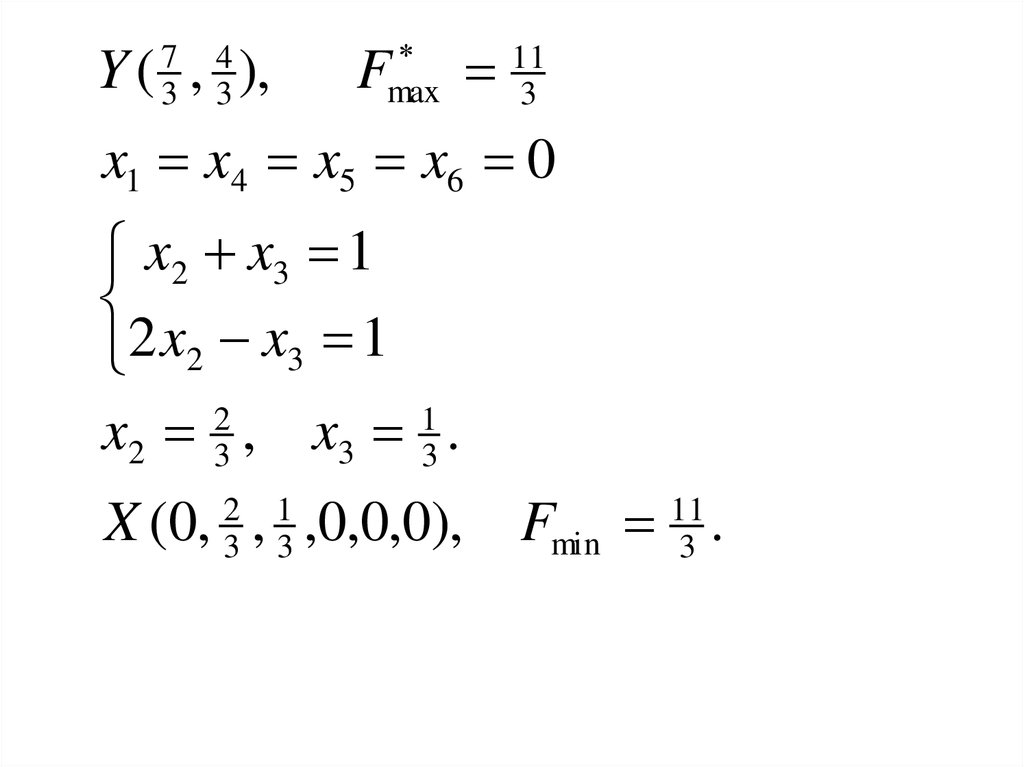



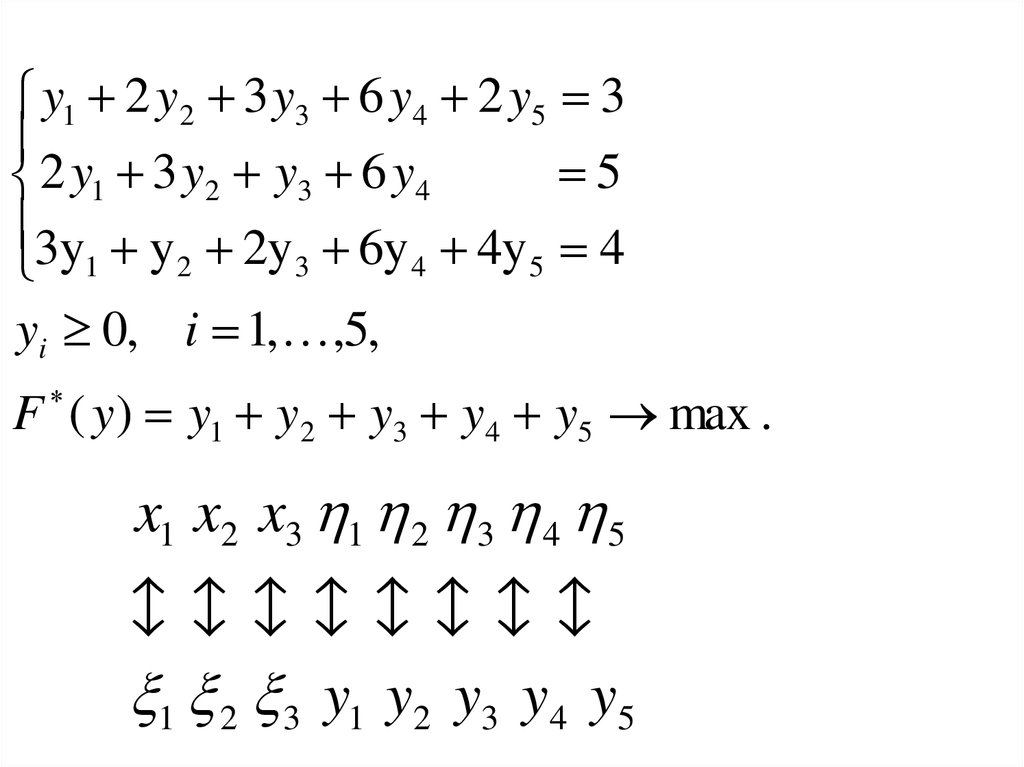


 Математика
Математика








