Похожие презентации:
Приложения химической термодинамики. Термодинамика фазовых равновесий
1. Приложения химической термодинамики
Термодинамика фазовыхравновесий
2. Фазовые равновесия в одно- и многокомпонентных системах
3.
Система называется гетерогенной, если онасостоит из двух или более фаз.
Фаза - совокупность однородных частей системы,
одинаковых по физическим, химическим и
термодинамическим свойствам, отделенная от
других частей системы поверхностью раздела.
4.
Если вещество содержится одновременно вразных фазах и происходит его переход из одной
фазы и другую, то такой переход называется
фазовым. Состояние, при котором скорости
противоположных фазовых переходов равны,
называется фазовым равновесием.
Условие равновесия фаз:
dG VdP SdT
P,T const :
( A
ПОЛ
0)
dG 0; G 0; i i ...
5. Гетерогенные системы классифицируют по числу компонентов (одно- и многокомпонентные).
Гетерогенныесистемы
классифицируют
компонентов (одно- и многокомпонентные).
по
числу
Компонентами (составляющими веществами) называются
индивидуальные химические вещества, которые могут быть
выделены из системы и существовать вне ее (I).
Число независимых компонентов (К) – минимальное число
компонентов, необходимое для образования каждой из фаз
данной системы.
I=K, если между компонентами системы отсутствуют
химические взаимодействия.
K = I – r , r – число уравнений, связывающих концентрации
компонентов системы.
CaCO3 CaO CO2
K 3 1 2
CaO CO2
K
CaCO3
6. Диаграммы, отражающие фазовый состав системы, называют фазовыми диаграммами или диаграммами состояния (объемные и плоские). Принципы фазо
Диаграммы, отражающие фазовый состав системы,называют
фазовыми
диаграммами
или
диаграммами состояния (объемные и плоские).
Принципы фазового анализа:
1) Принцип непрерывности: при непрерывном изменении
параметров состояния системы свойства системы в
пределах фазы также меняются плавно и непрерывно. При
появлении новой фазы или исчезновении старых свойства
системы меняются скачкообразно.
2) Принцип геометрического соответствия: на
диаграмме состояния каждому фазовому состоянию
системы соответствует свой геометрический образ
(плоскость, линия, точка).
7.
3) Правило фаз Гиббса:С=К–Ф+n
С – число степеней свободы или вариантность
системы – это число параметров состояния
системы, которые можно одновременно изменить
без изменения её фазового состава;
К – число независимых компонентов системы;
Ф – число фаз в данной точке системы;
n – число параметров состояния, характеризующих
систему.
8.
Однокомпонентные системы.Уравнение Клаузиуса-Клапейрона
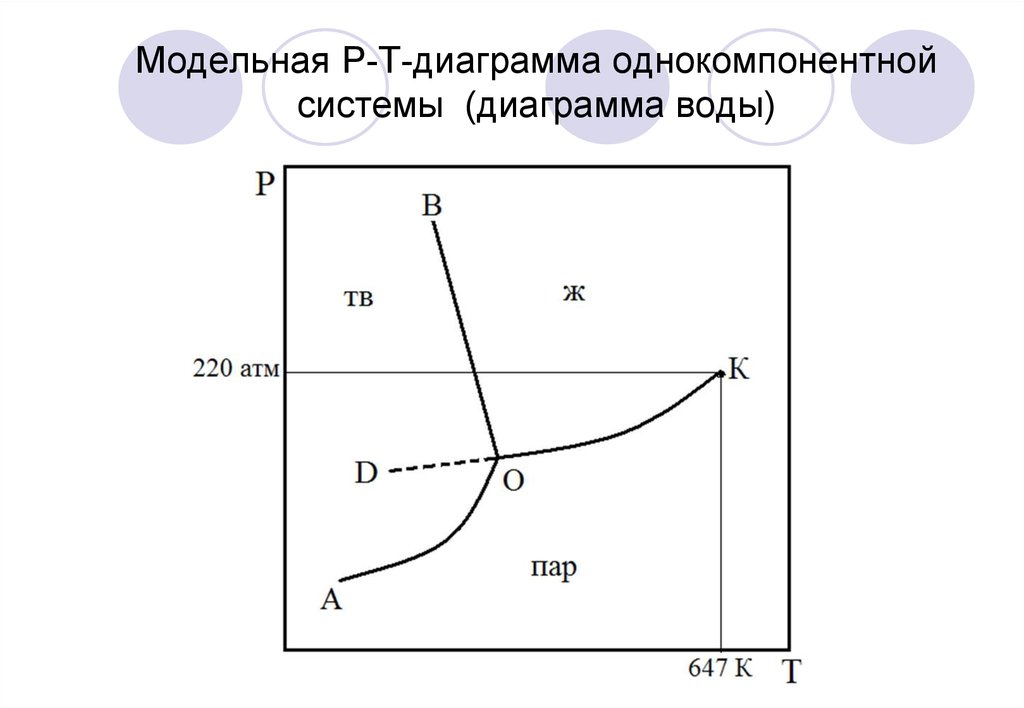
9. Модельная Р-Т-диаграмма однокомпонентной системы (диаграмма воды)
10.
ОА – линия возгонки (сублимации)ОВ – линия плавления (кристаллизации)
ОК – линия испарения (конденсации)
О – тройная точка
К – критическая точка
ОД – линия переохлажденной воды
(метастабильная фаза)
μ метастаб. фазы > μТД уст. фазы
11.
С=К–Ф+nС=1–Ф+2=3–Ф
точка 1 С = 3 – 1 = 2 (1/2)
точка 2
С = 3 – 2 = 1 (2/1)
точка О С = 3 – 3 = 0 (3/0)
12. Вывод и анализ уравнения Клаузиуса-Клапейрона
равновесие жидкость парЖ
П
G G
Ж
(1)
П
( A
dG VdP SdT
ПОЛ
0)
dG dG
Ж
(2)
(3)
П
V dP S dT V dP S dT
(4)
S dT S dT V dP V dР
(5)
( S S )dT (V V )dР
(6)
Ж
Ж
П
П
Ж
П
П
Ж
ФП
П
Ж
П
Ж
Н
Ж
П
dP S S
dT V V
S
П
ФП
Ж
S
V
/Т
ИСП
ФП
(7)
(8)
13.
dPH
dT T V
ФП
ФП
ФП
9
V
ИСП
V V V 0
П
Ж
П
P
tg
0
T
V
V V V 0
tg
P
0
T
V
V V 0
ВОЗГ
П
ПЛ
ТВ
Ж
П
ТВ
P
tg
0
T
V
ПЛ
V V 0
tg
V
ПЛ
Ж
ТВ
P
0
T
V V 0
tg
Ж
P
0
T
ТВ
14. Интегрирование уравнения Клаузиуса-Клапейрона
dPH
dT T V
9
ФП
ФП
ФП
для процессов испарения и возгонки б)
dP
10
V V
dT ТV
dP
PV RT
P 11
dT RТ
dP
dT 12
P
RТ
а)
H dT
d
ln
P
, H f Т
R
T
P2 H
1 1
ln
13
P1
R
T T
ФП
ФП
П
П
ФП
2
ФП
2
2
H
dT
d ln P
, H f Т
R
T
H
1
ln P
const 14
R T
H
10
lg P
const 15
2,303 R 10 T
ФП
2
ФП
3
ФП
3
2
ФП
2
1
1
ФП .
1
2
P e
фп / RT
Р Ae
econst
фп / RT
16
15.
H ф.п.(ln P)
tg
(1 / T )
R
H ф.п.
(lg P)
tg
3
(10 / T )
2,303 R 10 3
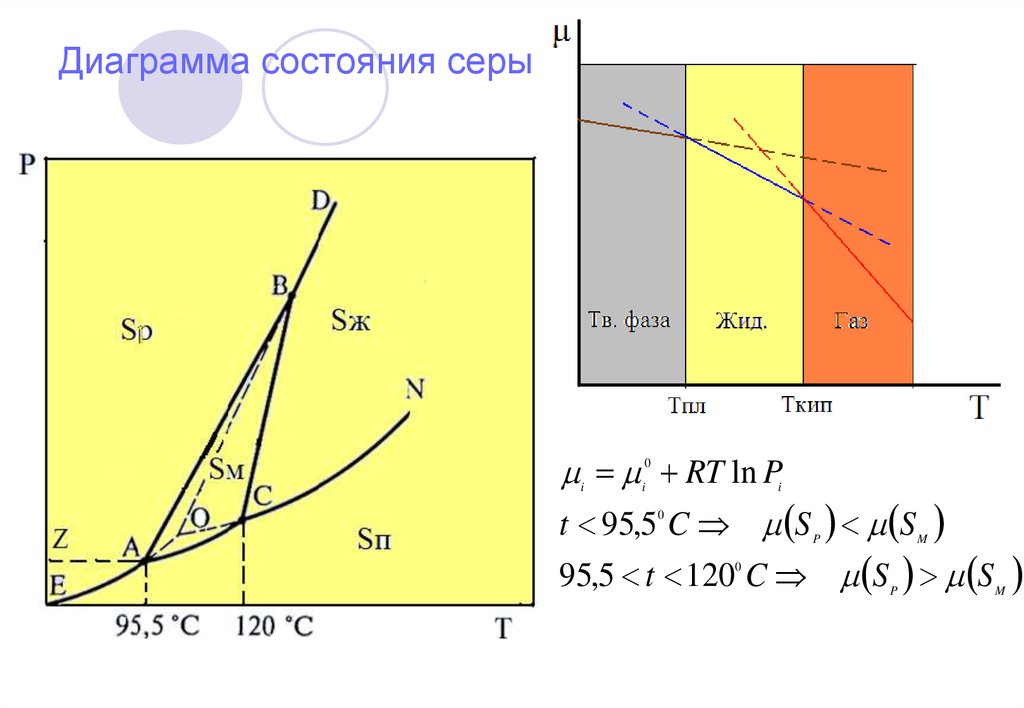
16. Диаграмма состояния серы
RT ln Pt 95,5 C S S
95,5 t 120 C S S
0
i
i
i
0
P
M
0
P
M














 Физика
Физика








