Похожие презентации:
Минимальные КНФ
1.
Минимальные КНФ2. Минимальные КНФ
3. Минимальные КНФ
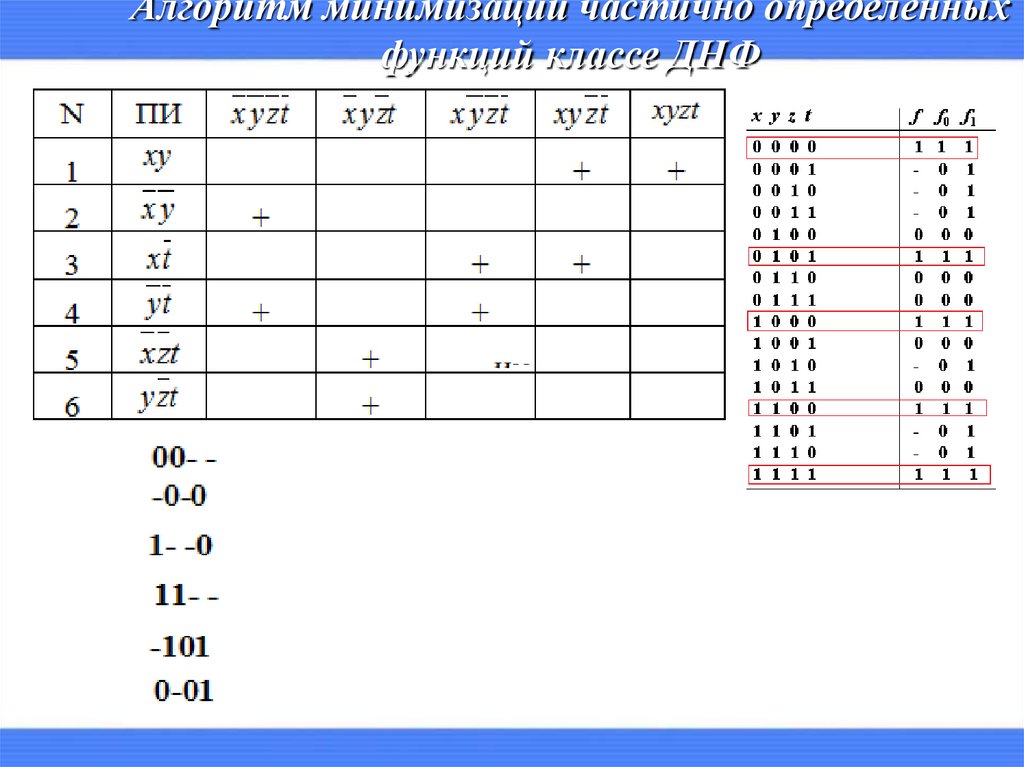
4. Алгоритм минимизации частично определенных функций классе ДНФ
1. СДНФ функции f0 .2. сокращенная ДНФ функции f1 .
3. С помощью матрицы покрытий коституент
единицы функции f0 простыми импликантами
функции f1 строим все тупиковые ДНФ (для
некоторых доопределений функции f ) .
4. Среди полученных ТДНФ выбираем простейшие,
они являются минимальными ДНФ ( для некоторых
доопределений функции f ) .
5. Алгоритм минимизации частично определенных функций классе ДНФ
6. Алгоритм минимизации частично определенных функций классе ДНФ
7. Алгоритм минимизации частично определенных функций классе ДНФ
f ( x, y, z, t ) = (1---010010-01--1)x y z t
f f0 f1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
1
0
1
0
0
1
0
0
1
1
1
0
0
0
0
1
0
0
1
0
0
0
1
0
0
1
1
1
1
1
0
1
0
0
1
0
1
0
1
1
1
1
0000
------0001
0010
1000
-----0011
0101
1010
1100
-----1101
1110
------1111
8.
Алгоритм минимизации частично определенныхфункций классе ДНФ
0000 +
------0001 +
0010 +
1000 +
-----0011 +
0101 +
1010 +
1100 +
-----1101 +
1110 +
------1111 +
00000-0
-000
----00-1
0-01
001-010
10-0
1-00
-----
-101
1-10
11011-0
-------11-1
111-
9.
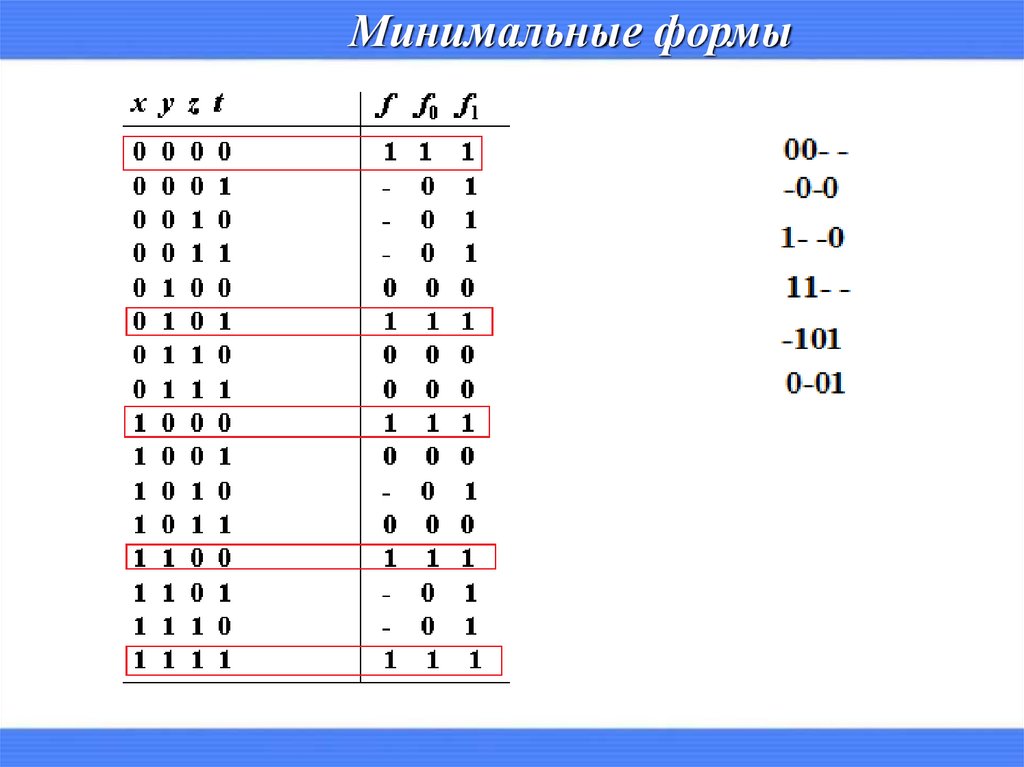
Минимальные формы0000 +
------0001 +
0010 +
1000 +
-----0011 +
0101 +
1010 +
1100 +
-----1101 +
1110 +
------1111 +
000- +
00-0 +
-000 +
----00-1 +
0-01
001- +
-010 +
10-0 + -101
1-00 + 1-10 +
110- +
----11-0 +
-------11-1 +
111- +
00- -0-0
-----1- -0
------11- -
10.
Минимальные формы11.
Алгоритм минимизации частично определенныхфункций классе ДНФ
12.
Алгоритм минимизации частично определенныхфункций классе ДНФ
13.
Алгоритм минимизации частично определенныхфункций классе ДНФ
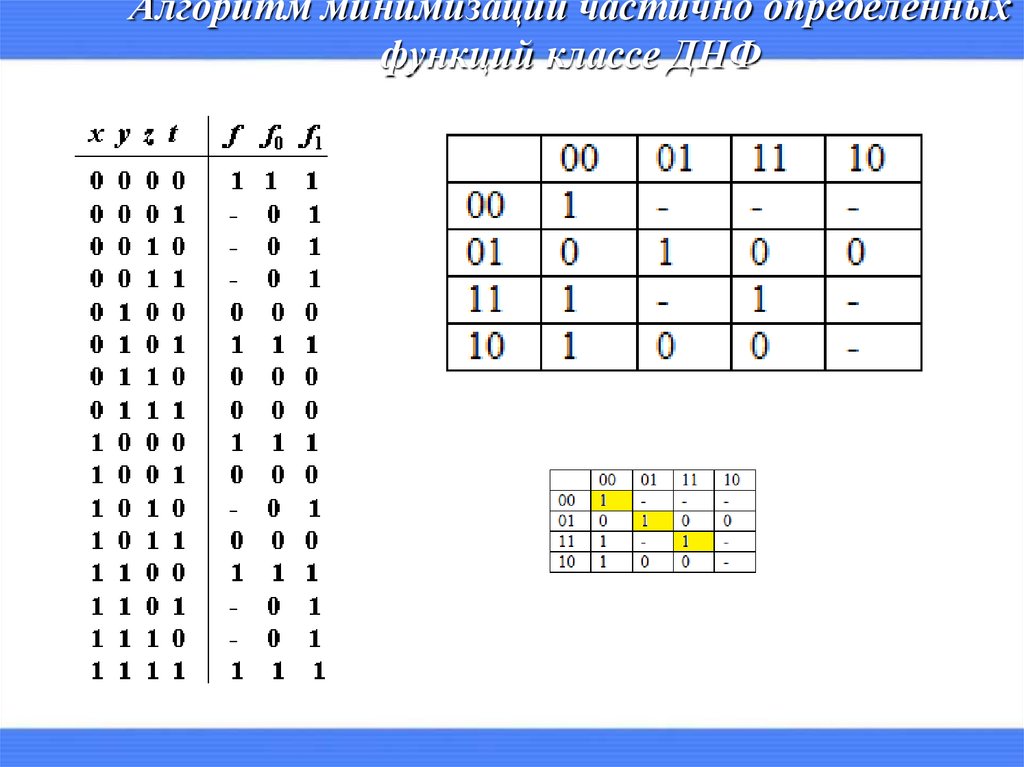
14. Алгоритм минимизации частично определенных функций классе ДНФ
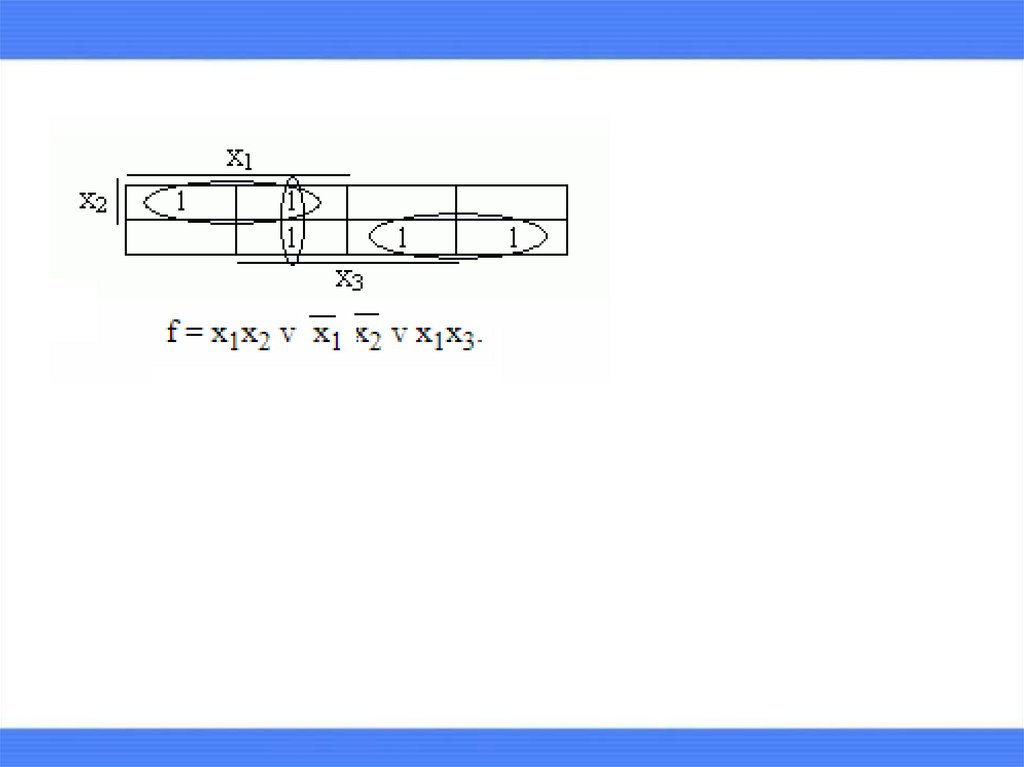
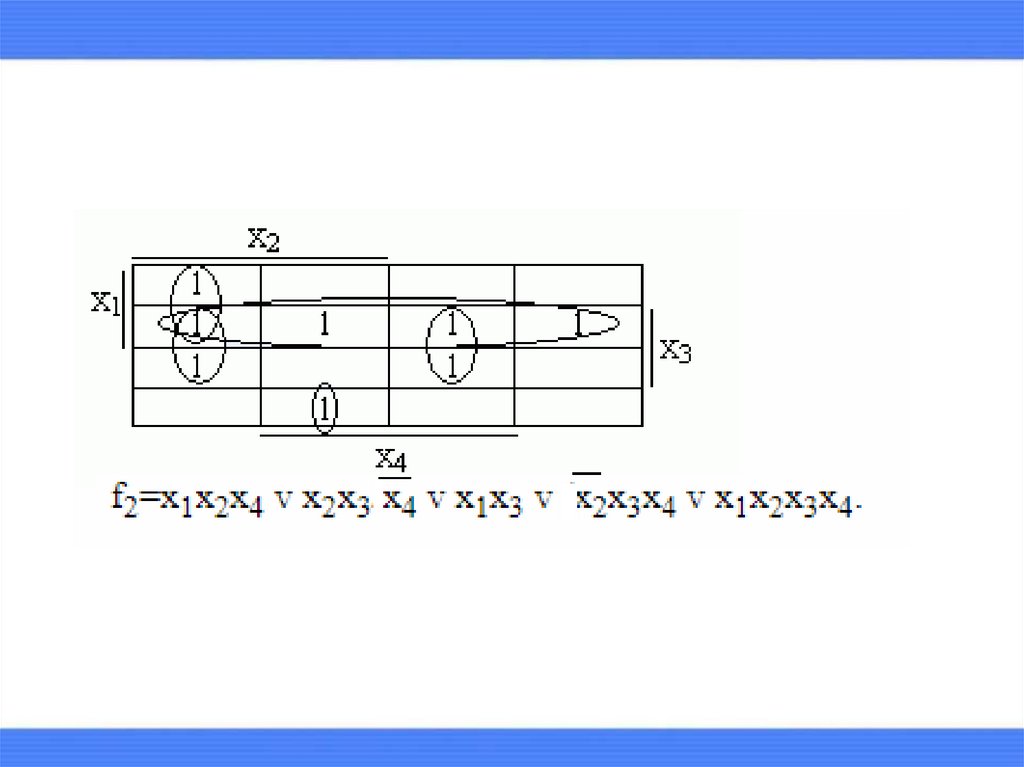
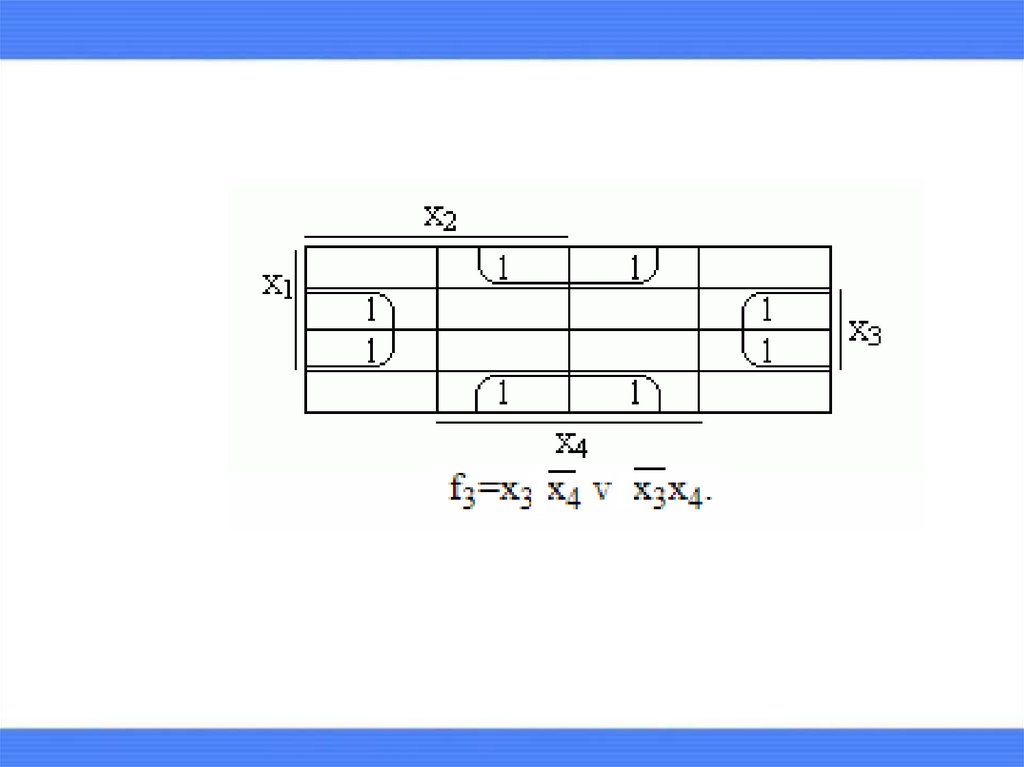
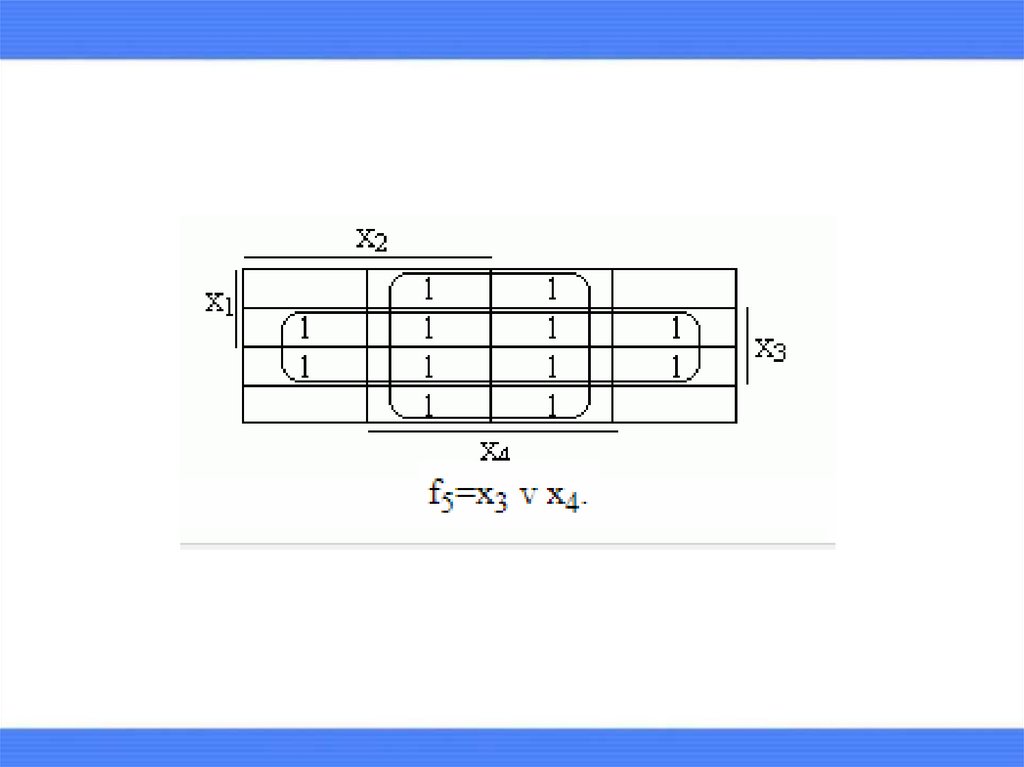
выделяются максимальные прямоугольники,содержащие хотя бы одну единицу и не содержащие
нулей.
D cf x 1 x 3 x 1 x2 x2 x3 x1 x3 .
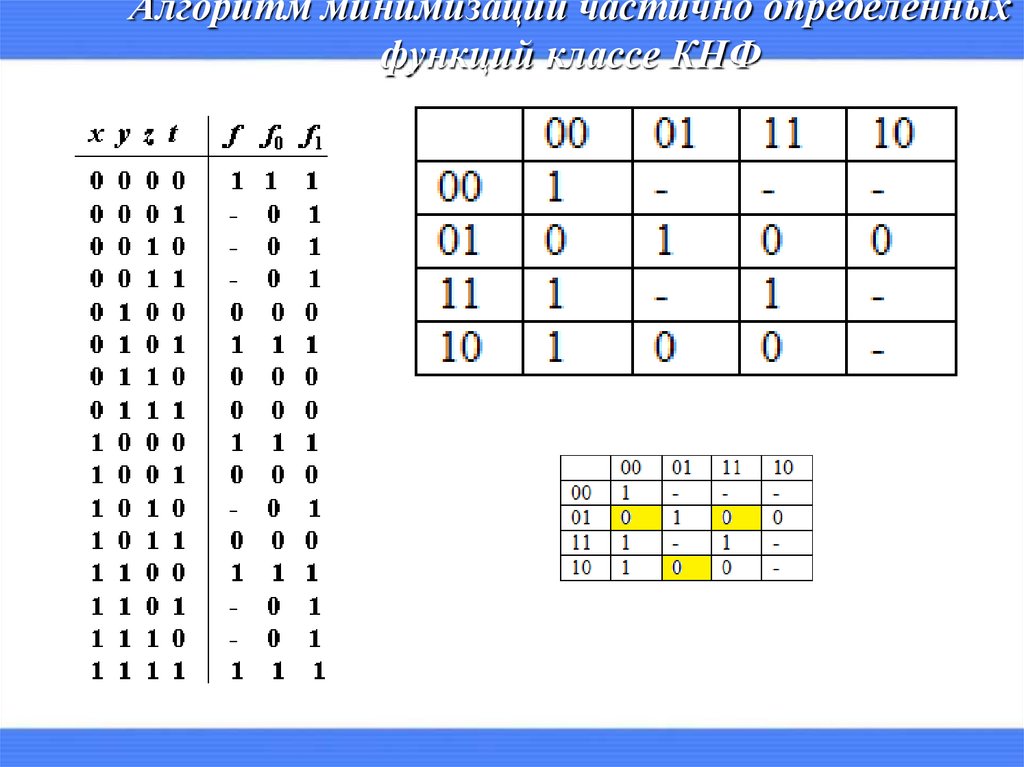
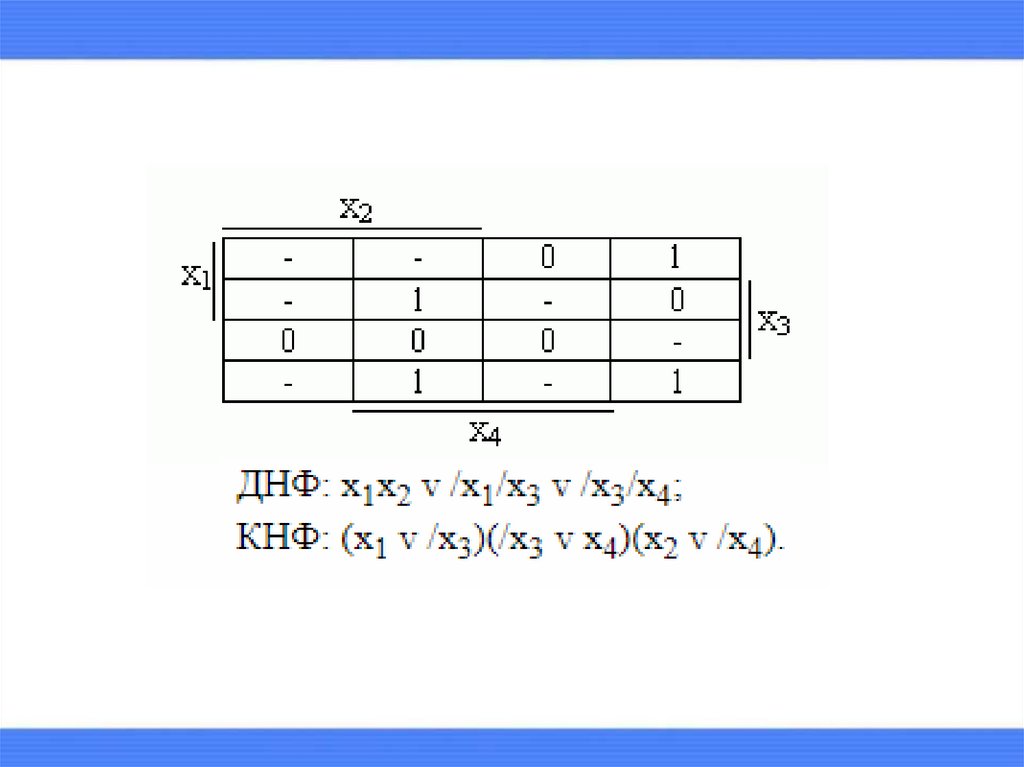
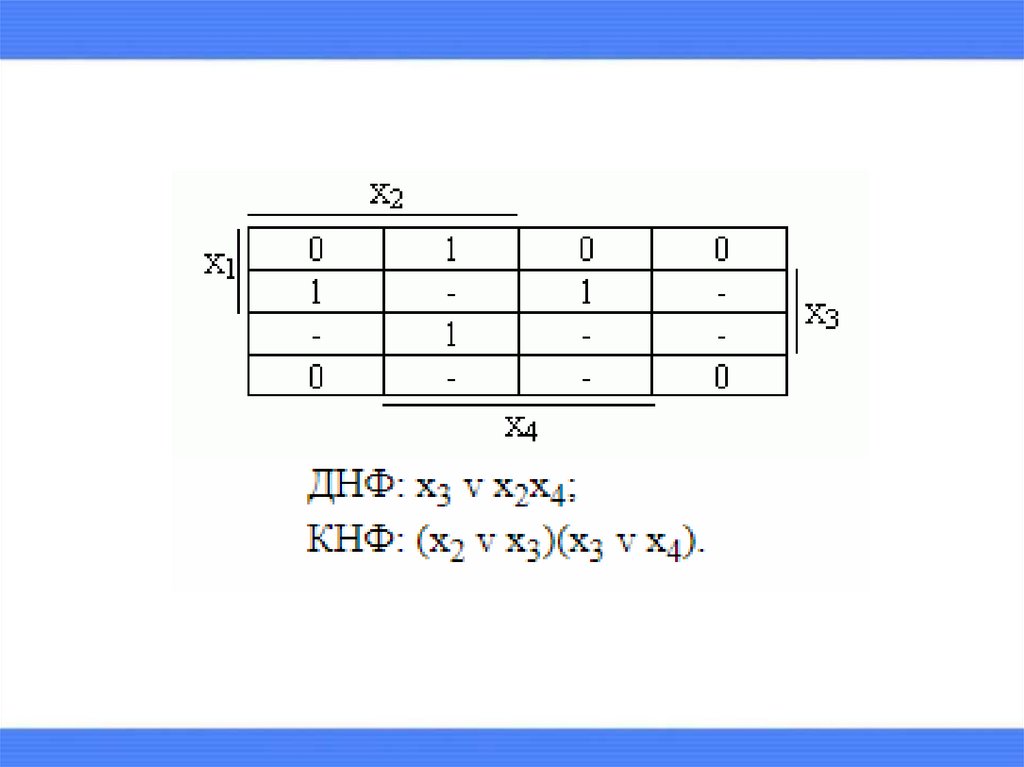
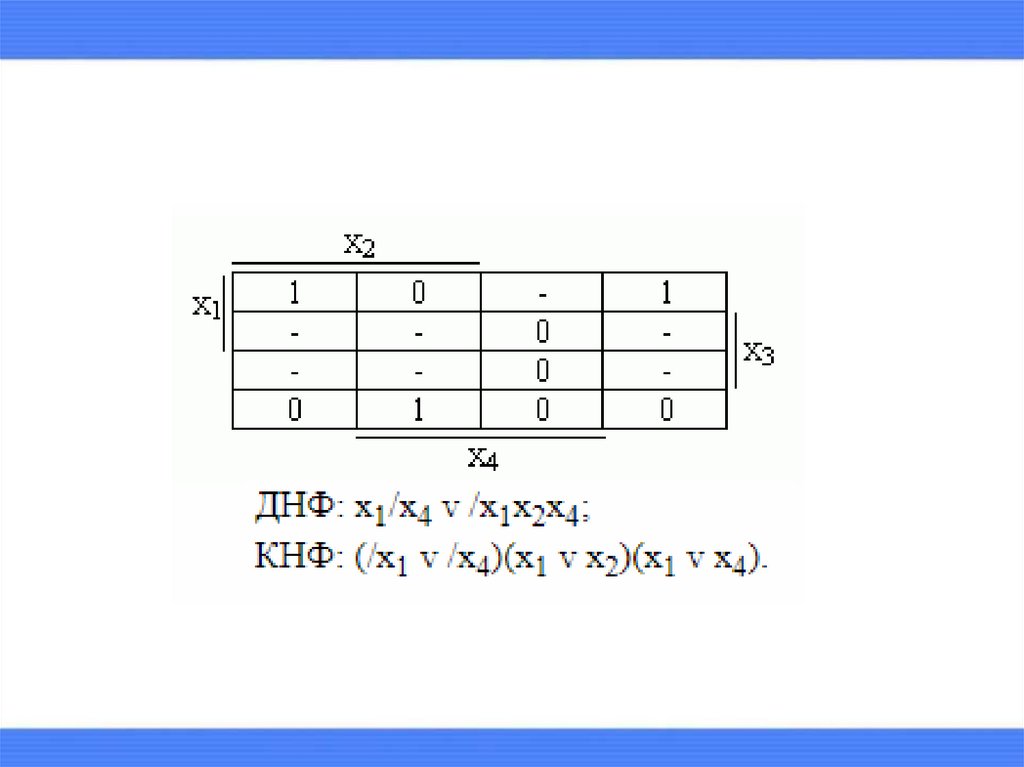
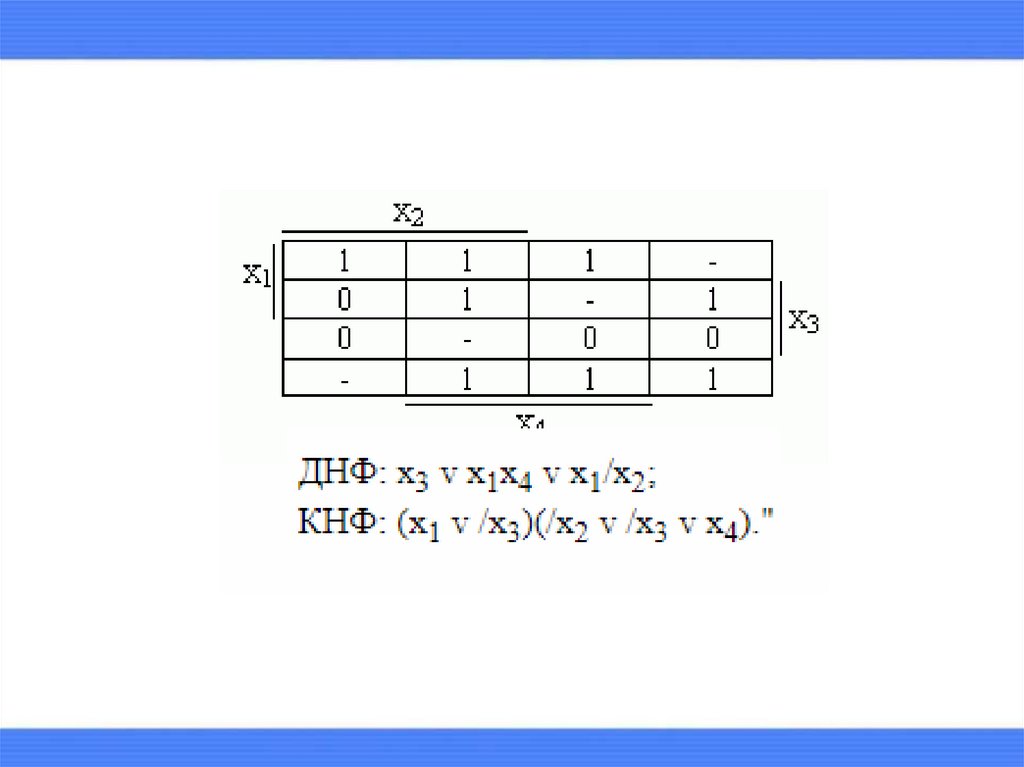
15. Алгоритм минимизации частично определенных функций классе ДНФ
16.
Алгоритм минимизации частично определенныхфункций классе КНФ
x y z t
f f0 f1 f
h0 h1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
1
0
1
0
0
1
0
0
1
1
0
0
0
0
1
0
1
1
0
1
0
1
0
0
0
0
1
0
0
0
0
1
0
0
1
0
0
0
1
0
0
1
1 0
1 1 1 0 1
1 0
0 1
0 1
1 0
0 1
1 0 1
1 0
1 1 1 0
0
1
1
1
1
0
1
1
0
1
1
1
0
1
1
0
0001
0010
0100
------0011
0110
1001
1010
------0111
1011
1101
1110
17. Алгоритм минимизации частично определенных функций классе КНФ
0001 +0010 +
0100 +
------0011 +
0110 +
1001 +
1010 +
------0111 +
1011 +
1101 +
1110 +
00-1
-011
0010-10
-010
01-0
------0-11
-011
011-110
10-1
1011-10
1-01
18. Алгоритм минимизации частично определенных функций классе КНФ
0001 +0010 +
0100 +
------0011 +
0110 +
1001 +
1010 +
------0111 +
1011 +
1101 +
1110 +
00-1 +
-011 +
001- +
0-10 +
-010 +
01-0
------0-11 +
-011 +
011- +
-110 +
10-1 +
101- +
1-10 +
1-01
-0-1
0-1-01--10
-0-1
0-1-01--10
01-0
1-01
19. Алгоритм минимизации частично определенных функций классе КНФ
-0-10-1-01--10
01-0
1-01
20. Алгоритм минимизации частично определенных функций классе КНФ
-0-10-1-01--10
01-0
1-01
21. Алгоритм минимизации частично определенных функций классе КНФ
22. Алгоритм минимизации частично определенных функций классе КНФ
-минимальное доопределение функции f в классе КНФ23. Алгоритм минимизации частично определенных функций классе КНФ
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
Метод испытания импликантf (~
x 3 ) x1x3 x4 x2 x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
x1 x3 x4
x1 0
x3 1
x4 1
0 1 1
0 1 1
1 0 1
1 0 0
0 0 0
3
~
f ( x ) x2 x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
f (~
x 3 ) x2 1 1 0 x2 1 0 x2 0 x2 0 0 нельзя
x2 0 0 0
x2
ядро
36.
Метод испытания импликантf (~
x 3 ) x1x3 x4 x2 x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
x2 x3 x4
x2 0
x3 1
x4 1
f (~
x 3 ) x1x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
f (~
x 3 ) x1 1 1 x1 1 1 x1 1 0 1 0 0
x1 x1 0 0
1
можно
не ядро
37.
Метод испытания импликантf (~
x 3 ) x1x3 x4 x2 x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
ядро
?
?
?
ядро
f (~
x 3 ) x1x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
ядро
ядро
38.
Метод испытания импликантf (~
x 3 ) x1x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
x1x2 x4
x1 1
x2 0
x4 1
3
~
f ( x ) 0 x3 0
нельзя
39.
Метод испытания импликантf (~
x 3 ) x1x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
x1x2 x3
x1 1
x2 0
x3 0
f (~
x 3 ) 0 0 x4 0 x4 1
можно
40.
Метод испытания импликантf (~
x 3 ) x1x3 x4 x2 x3 x4 x1x2 x4 x1x2 x3 x2 x3 x4
f (~
x 3 ) x1x3 x4 x1x2 x4 x2 x3 x4
41.
Операция штрих Шеффера42.
Операция штрих Шеффераправила перехода от ДНФ функции к выражению с
использованием операции " Штрих Шеффера ".
- заменить все операции дизъюнкции на операции
Шеффера
- заменить все операции конъюнкции на операции
Шеффера
- группы букв, которые соответствуют дизъюнктивным
членам, заключить в скобки.
43.
Операция (стрелка) Пирса44.
Операция штрих Шеффераправила перехода от от КНФ перейти к базису Пирса
- заменить операции дизъюнкции операциями Пирса
- заменить операции конъюнкции операциями Пирса
- заключить в скобки все те группы букв, которые
соответствуют конъюнктивным членам.





































 Математика
Математика








