Похожие презентации:
Линейная функция и ее график
1.
2.
ПовторениеФункция вида у = kx + b называется
линейной.
Графиком функции вида у = kx +b
является прямая.
Для построения прямой необходимы
только две точки, так как через две
точки проходит единственная
прямая ( дополнительная третья
точка нужна для
проверки вычислений)
3.
Повторениеy = kx + b – линейная функция
х – аргумент (независимая переменная)
у – функция (зависимая переменная)
k, b – числа (коэффициенты)
4.
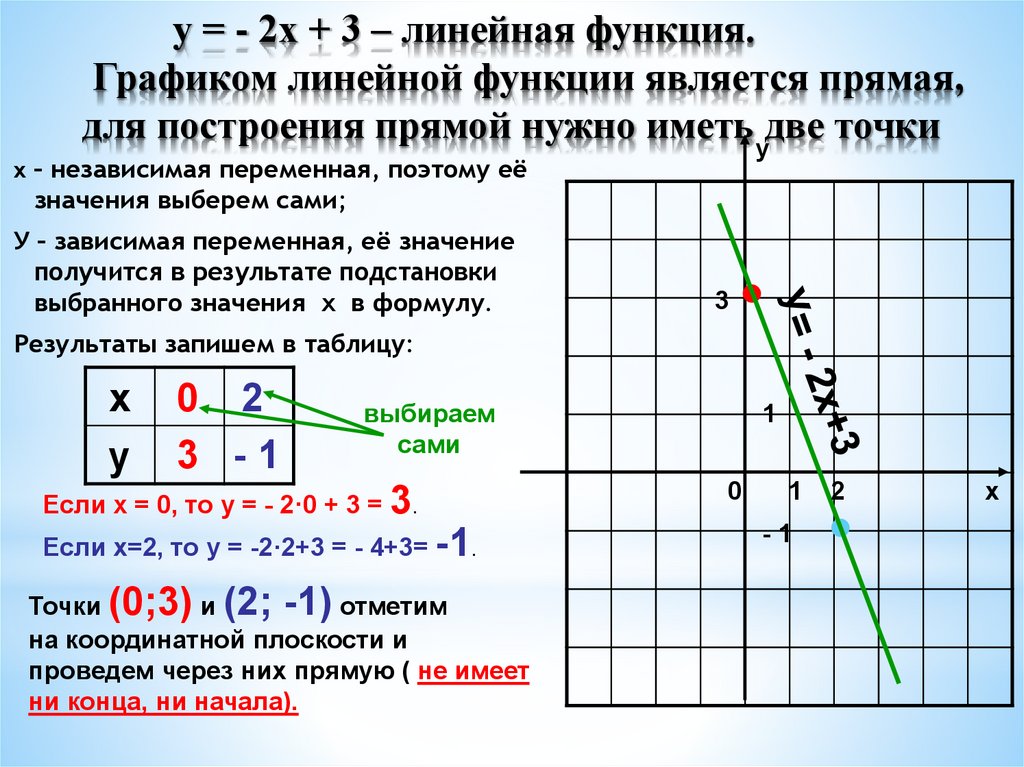
у = - 2х + 3 – линейная функция.Графиком линейной функции является прямая,
для построения прямой нужно иметьудве точки
х – независимая переменная, поэтому её
значения выберем сами;
У – зависимая переменная, её значение
получится в результате подстановки
выбранного значения х в формулу.
3
Результаты запишем в таблицу:
х
у
0 2
3 -1
выбираем
сами
Если х = 0, то у = - 2·0 + 3 = 3.
Если х=2, то у = -2·2+3 = - 4+3= -1.
Точки (0;3) и (2; -1) отметим
на координатной плоскости и
проведем через них прямую ( не имеет
ни конца, ни начала).
1
0
1
-1
2
х
5.
Если b=0, то линейная функция y =kx+bпримет вид y = kx
Функция вида y = kx называется прямой
пропорциональностью (k ≠ 0)
График прямой пропорциональности – прямая,
проходящая через начало координат (0;0)
y=kx, k>0
y=kx, k<0
y
II
I
III
O
x
y
O
IV
x
6.
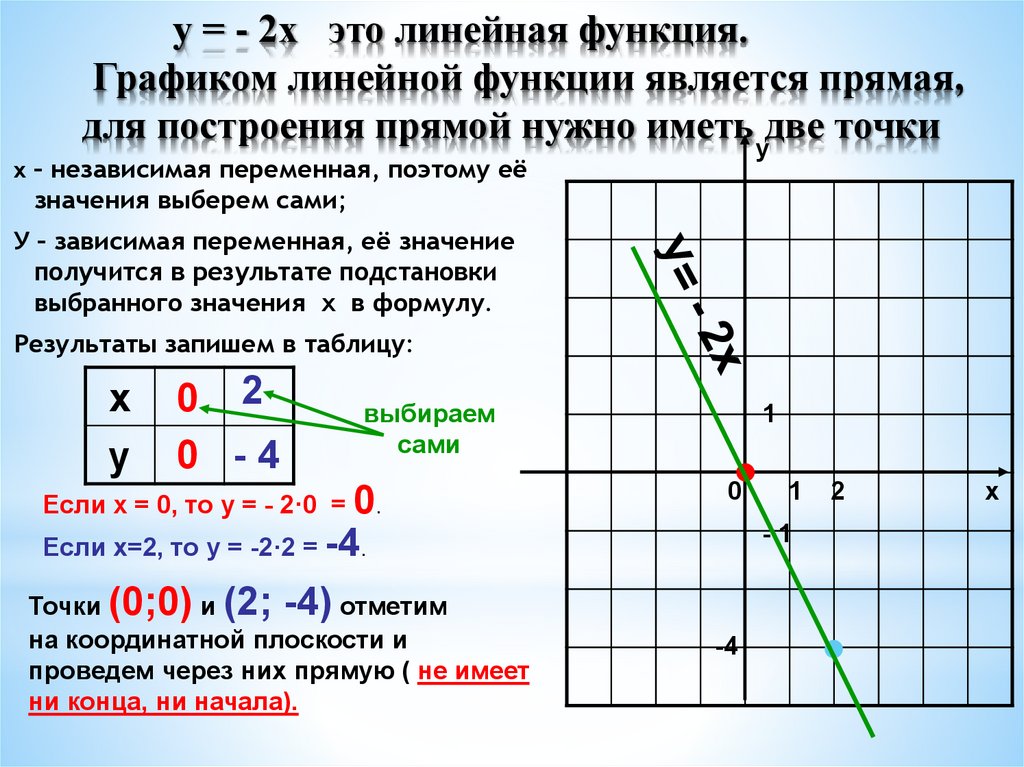
у = - 2х это линейная функция.Графиком линейной функции является прямая,
для построения прямой нужно иметьудве точки
х – независимая переменная, поэтому её
значения выберем сами;
У – зависимая переменная, её значение
получится в результате подстановки
выбранного значения х в формулу.
Результаты запишем в таблицу:
х
у
0 2
0 -4
выбираем
сами
Если х = 0, то у = - 2·0 = 0.
1
0
-1
Если х=2, то у = -2·2 = -4.
Точки (0;0) и (2; -4) отметим
на координатной плоскости и
проведем через них прямую ( не имеет
ни конца, ни начала).
1
-4
2
х
7.
Если k=0, то линейная функция y =kx+bпримет вид y = b ( b- любое число)
Примеры:
1) у = 2,5
2) у =-6,1
k = 0; b=2,5
k = 0; b= -6,1
8.
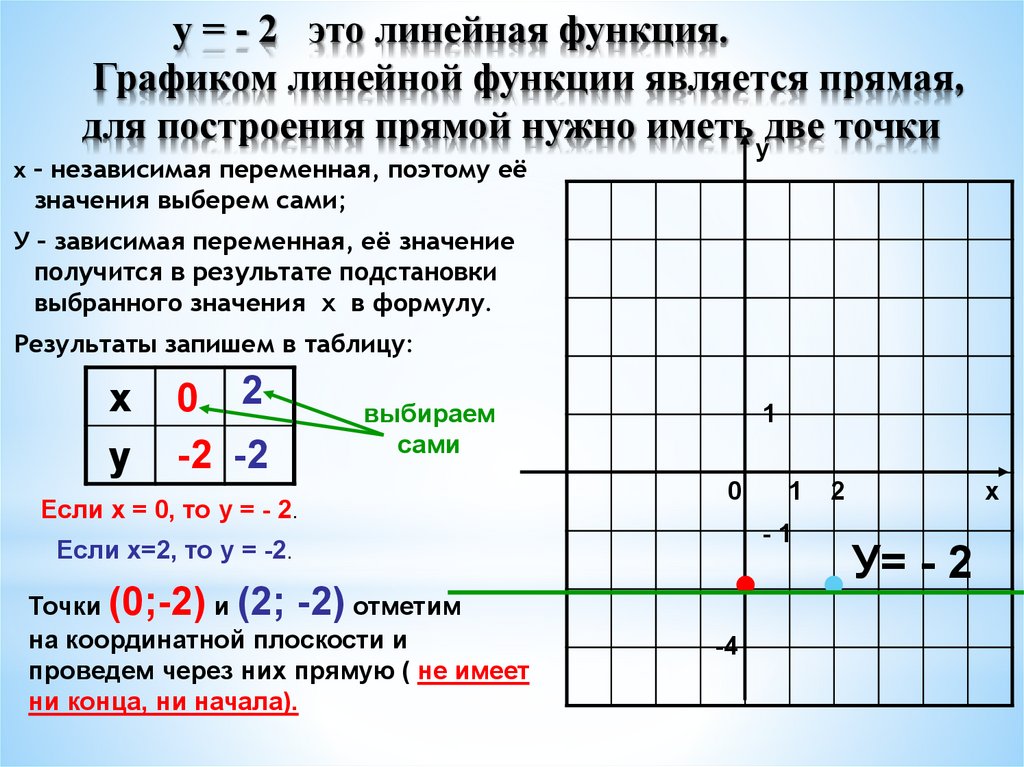
у = - 2 это линейная функция.Графиком линейной функции является прямая,
для построения прямой нужно иметьудве точки
х – независимая переменная, поэтому её
значения выберем сами;
У – зависимая переменная, её значение
получится в результате подстановки
выбранного значения х в формулу.
Результаты запишем в таблицу:
х
у
0 2
-2 -2
выбираем
сами
Если х = 0, то у = - 2.
1
0
-1
Если х=2, то у = -2.
Точки (0;-2) и (2; -2) отметим
на координатной плоскости и
проведем через них прямую ( не имеет
ни конца, ни начала).
1
-4
х
2
У= - 2
9.
Если к=0, то линейная функция y =kx+bпримет вид y = b
График функции y = b – прямая,
параллельная оси х ( абсцисс)
y
y= b (b >0)
O
y= b
x
(b < 0)
10.
!!! Записать в тетрадьЛЕЖАТ ЛИ ТОЧКИ А(1;2), В(-2;9),С(3;-4),
D(-7;26),Е(10;-35) на графике функции
у=-3х+5?
Нужно подставить координаты точек в формулу и
проверить верны ли равенства.
1)А(1;2)
х у
При х=1
у=-3∙1+5=-3+5=2
2=2, значит точка А лежит на графике функции.
2)В(-2;9)
х у
При х=-2
у=-3∙(-2)+5=6+5=11
9 ≠ 11 , значит точка В не лежит на
графике функции.
11.
*Это нужно знать:1. Если точка лежит на оси
у(ординат), ее абсцисса
равна нулю. ( 0;У)
2. Если точка лежит на оси
х (абсцисс,) ее ордината
равна нулю.
( Х;0)
12.
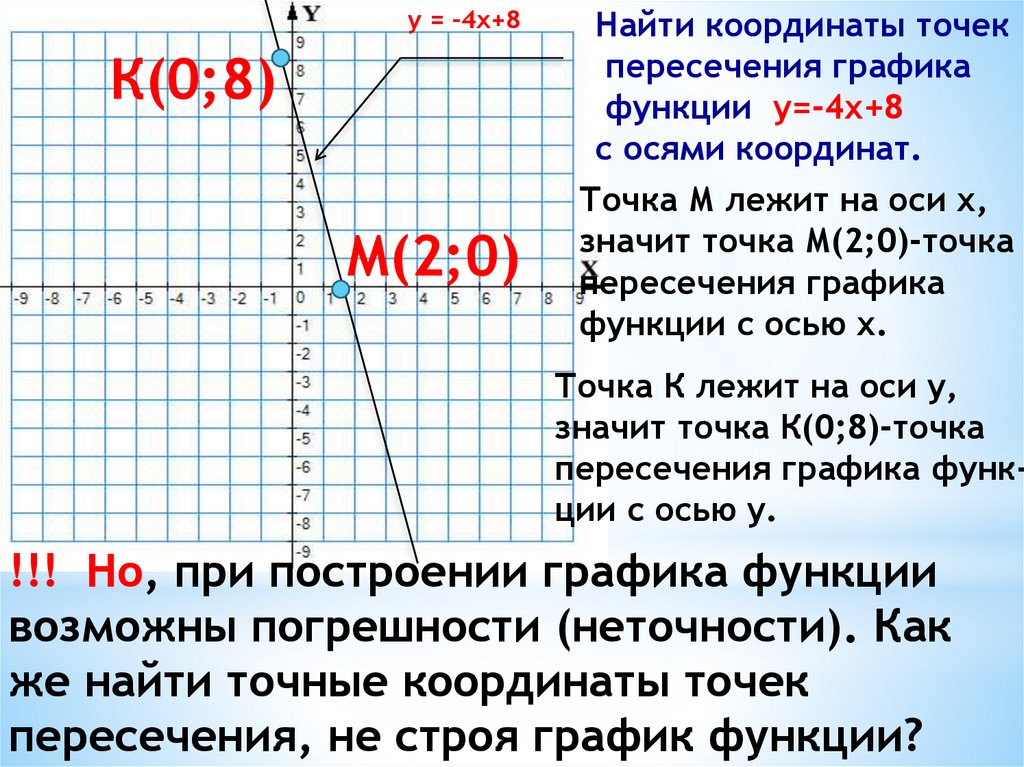
у = -4х+8К(0;8)
М(2;0)
Найти координаты точек
пересечения графика
функции у=-4х+8
с осями координат.
Точка М лежит на оси х,
значит точка М(2;0)-точка
пересечения графика
функции с осью х.
Точка К лежит на оси у,
значит точка К(0;8)-точка
пересечения графика функции с осью у.
!!! Но, при построении графика функции
возможны погрешности (неточности). Как
же найти точные координаты точек
пересечения, не строя график функции?
13.
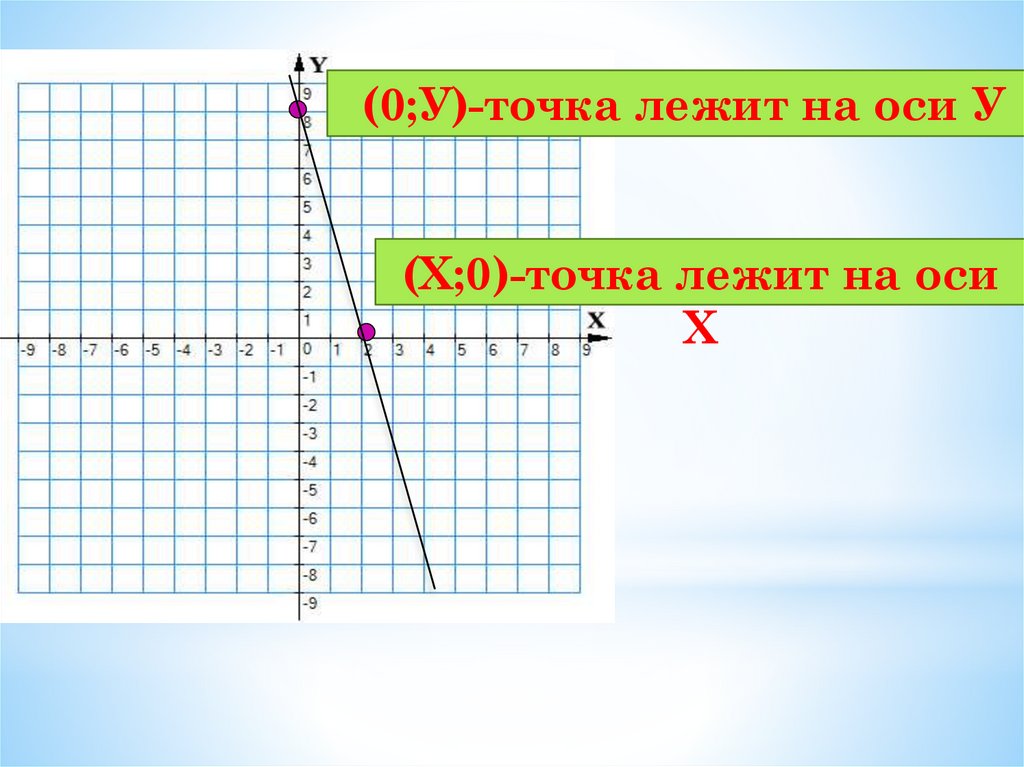
(0;У)-точка лежит на оси У(Х;0)-точка лежит на оси
Х
14.
!!! Записать в тетрадьНе выполняя построения, найти точки пересечения
графика функции у=-4х+8 с осями координат.
1)Пусть М(х;0)-точка пересечения графика функции с
осью х
(у=0,так как точка лежит на оси х). Найдем х.
При у = 0
-4х+8=0
-4х=-8|:(-4)
х=2
М(2;0)-точка пересечения графика функции с осью х.
2)Пусть К(0;у)-точка пересечения графика функции с
осью у
(х=0,так как точка лежит на оси у). Найдем у.
При х = 0
у=-4∙0+8 =0+8=8
К(0;8)-точка пересечения графика функции с осью у.
15.
Построениеграфика кусочной
функции.
16.
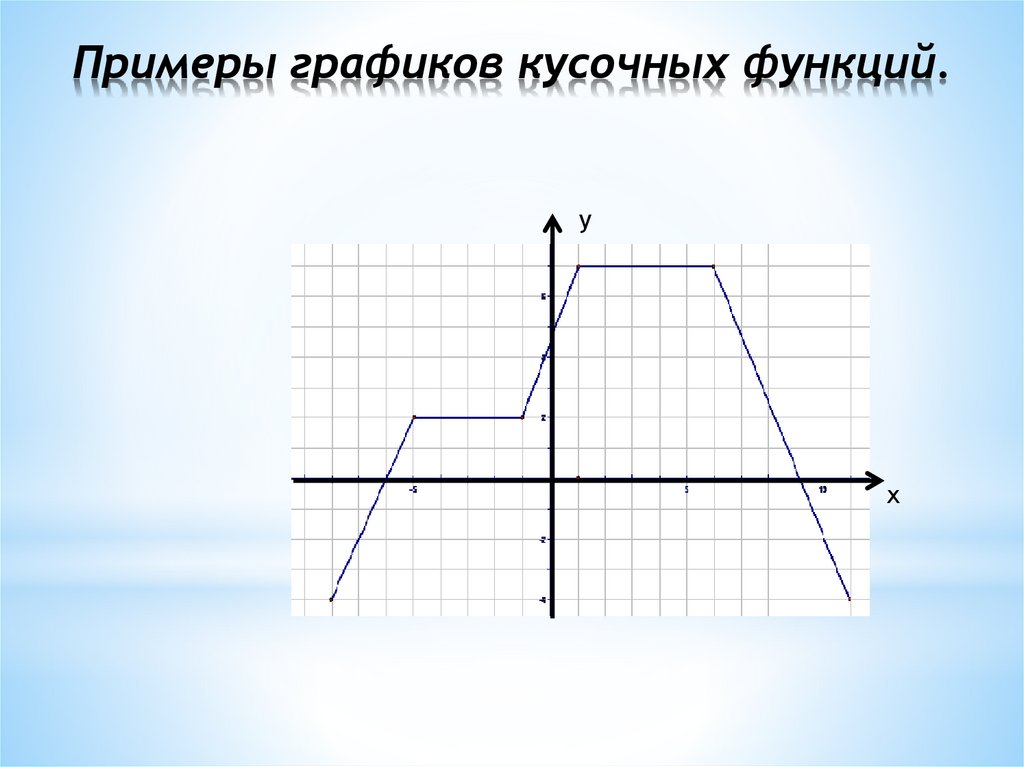
Примеры графиков кусочных функций.у
х
17.
Алгебраически такие функциизадаются в виде системы.
18.
Задание № 22 (2 часть из ОГЭ)Постройте график функции
и определите, при каких значениях с
прямая у = с имеет с графиком ровно две
общие точки.
19.
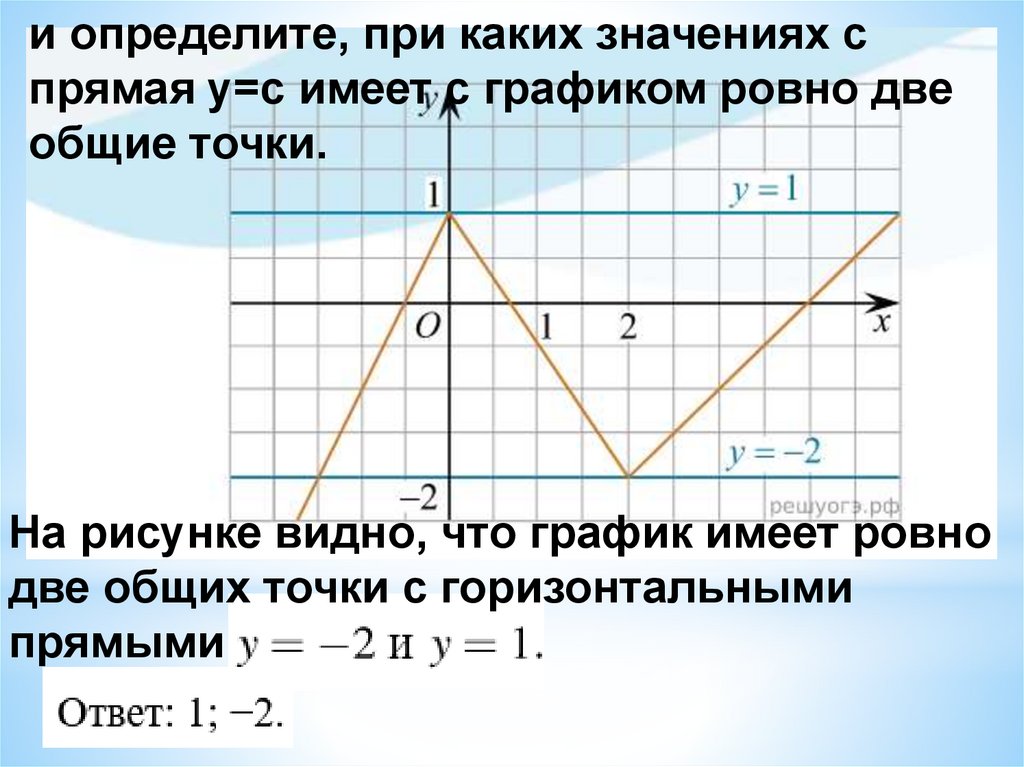
и определите, при каких значениях спрямая у=с имеет с графиком ровно две
общие точки.
На рисунке видно, что график имеет ровно
две общих точки с горизонтальными
прямыми
20.
21.
у1) у=х-4 ( х≥0) правее нуля
график- прямая
х 0 2
у -4 -2
1) у=-2х-4 ( х<0) левее нуля
график- прямая
х -1 -2 0
у -2 0 -4
1
-2
-1 0
-2
-3
1
2
х
22.
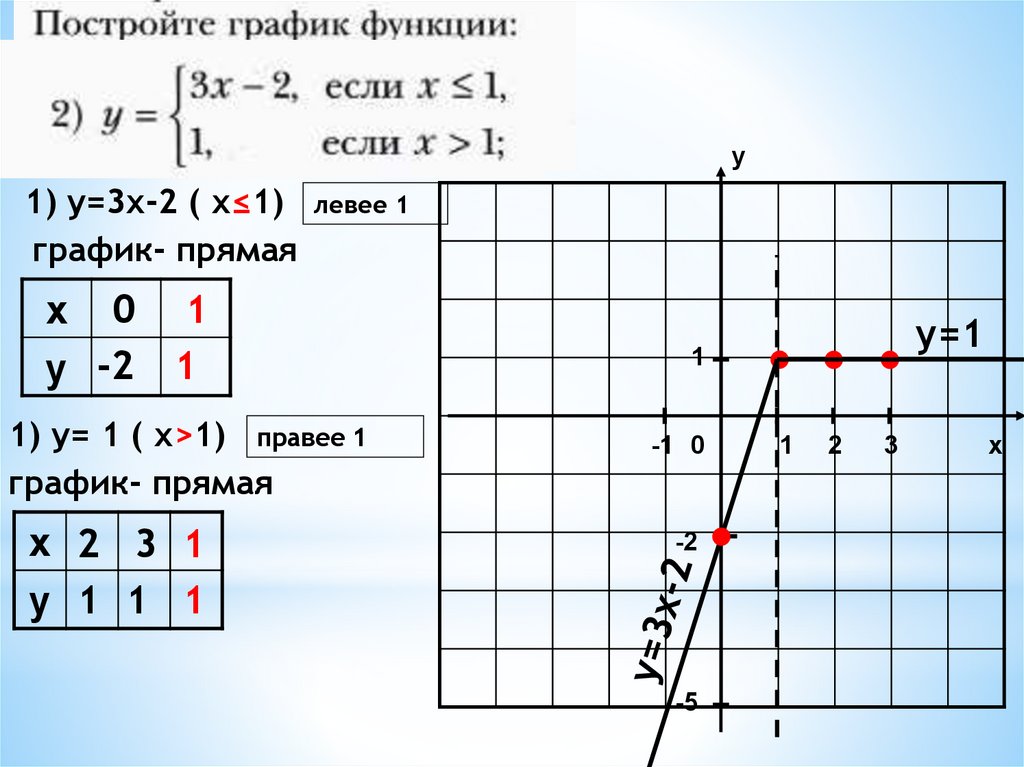
у1) у=3х-2 ( х≤1) левее 1
график- прямая
х 0 1
у -2 1
1) у= 1 ( х>1) правее 1
график- прямая
х 2 3 1
у 1 1 1
у=1
1
-1 0
-2
-5
1
2
3
х
23.
Домашняя контрольная работа6. Построить в одной системе координат графики функций у=1,5х-4; у=1,5х и у=1,5
















 Математика
Математика








