Похожие презентации:
Построение сечений (10 класс)
1.
2.
Секущей плоскостью многогранника называется любаяплоскость, по обе стороны от которой имеются точки
данного многогранника.
А
N
M
Секущая плоскость
α
пересекает грани
многогранника по
отрезкам.
Многоугольник,
сторонами которого
являются эти
В
отрезки, называется
сечением
многогранника.
K
D
С
3.
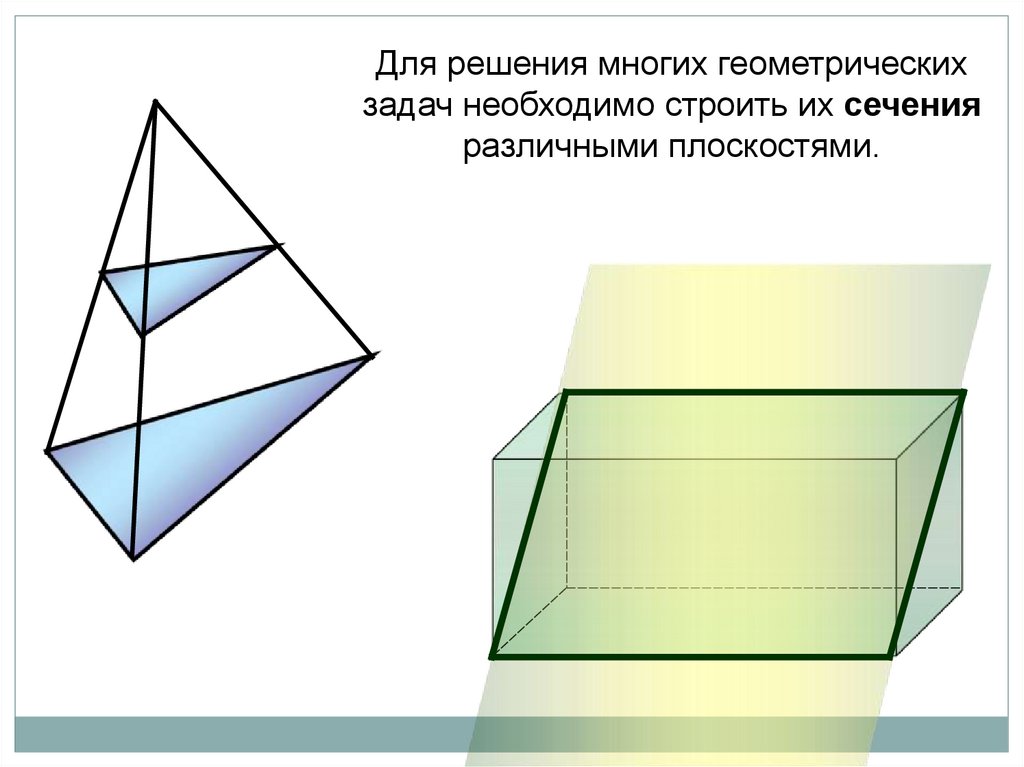
Для решения многих геометрическихзадач необходимо строить их сечения
различными плоскостями.
4.
Для построения сечения нужно построитьточки пересечения секущей плоскости с
ребрами и соединить их отрезками.
1. Соединять можно только две точки, лежащие в
плоскости одной грани.
2. Секущая плоскость пересекает
грани по параллельным отрезкам.
параллельные
3. Если в плоскости грани отмечена только одна точка,
принадлежащая плоскости сечения, то надо построить
дополнительную точку. Для этого необходимо найти
точки пересечения уже построенных прямых с другими
прямыми, лежащими в тех же гранях.
5.
AAB ∩ m = C
M
B
C
C
m
B
A
N
D
MN ∩ BA = K
Рис. 1
K
Рис. 2
6.
Построение сечений тетраэдраи параллелепипеда.
Исследовательская работа
«Какие фигуры могут получиться в
сечениях тетраэдра и
параллелепипеда плоскостью?»
7.
Построить сечение тетраэдра DABC плоскостью, проходящейчерез точки M,N,K
D
1. Проведем прямую через
D
точки М и К, т.к. они лежат
в одной грани (АDC).
M
N
A
A
K
B
B
C
2. Проведем прямую через
точки К и N, т.к. они лежат в
одной грани (СDB).
3. Аналогично рассуждая,
проводим прямую MN.
4. Треугольник MNK – искомое сечение.
8.
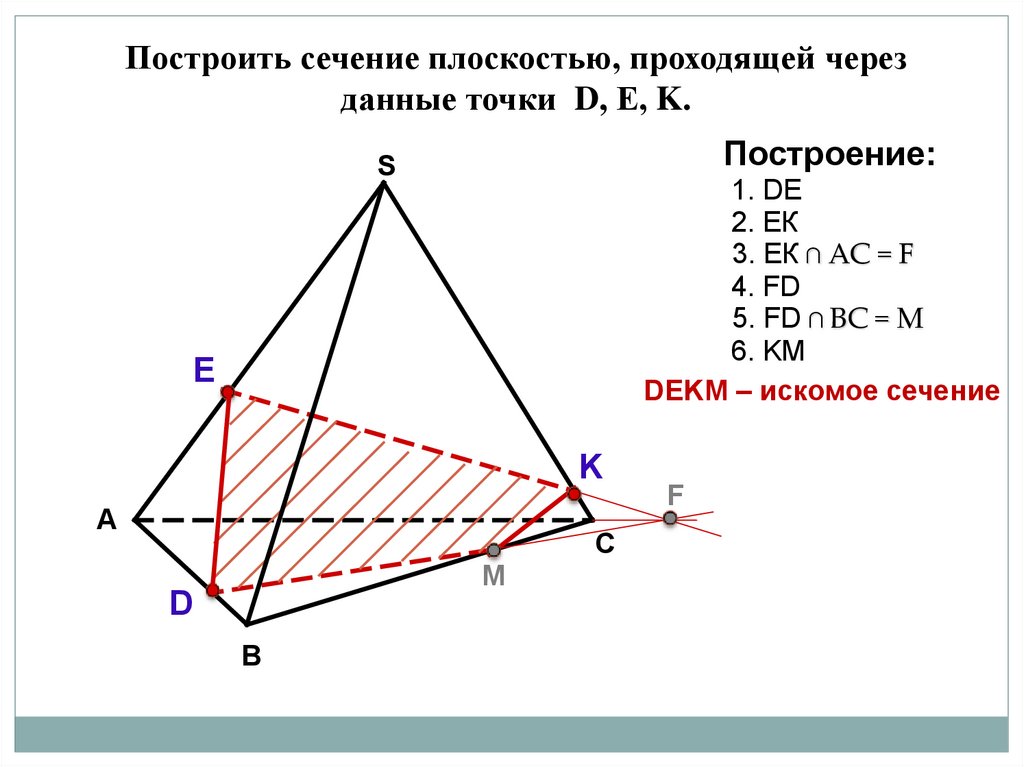
Построить сечение плоскостью, проходящей черезданные точки D, Е, K.
Построение:
S
1. DE
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
DЕKМ – искомое сечение
E
K
А
С
M
D
В
F
9.
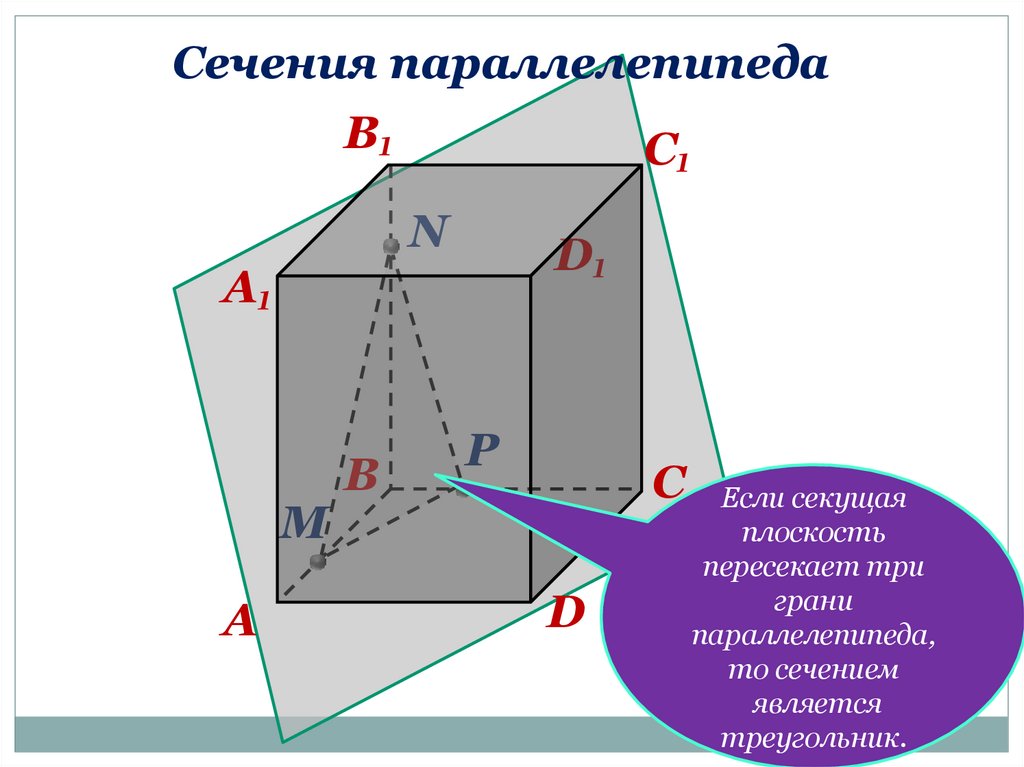
Сечения параллелепипедаB₁
C₁
N
D₁
A₁
M
A
B
P
C
D
Если секущая
плоскость
пересекает три
грани
∆ MNP
– сечение.
параллелепипеда,
то сечением
является
треугольник.
10.
B₁C₁
M
A₁
D₁
N
P
B
A
Q
D
Если секущая
плоскость
Cпересекает
4 грани
Четырёхугольник
параллелепипеда,
MNQP
то–сечение.
сечением
является
четырёхугольник.
11.
Построить сечение плоскостью, проходящей через точкиР, К, М, М∈ВС.
Построение:
В1
К
А1
Р
C1
D1
N
В
А
М
D
E
С
1. КP
2. EM ║ КP
3. EK
4. МN ║ EK
5. РN
KРNМE – искомое сечение
Если секущая
плоскость
пересекает 5 граней
параллелепипеда,
то сечением
является
пятиугольник.
12. Сечения параллелепипеда
Построить сечение плоскостью, проходящей через точкиК, L, М.
Построение:
T
К
В1
C1
F
E
А1
L
А
D1
В
P
С
G
D
М
N
1. ML
2. ML ∩ D1А1 = E
3. EK
4. EK ∩ А1B1 = F
5. LF
6. LM ∩ D1D = N
7. ЕK ∩ D1C1 = T
8. NT
9. NT ∩ DC = G
NT ∩ CC1 = P
10. MG
11. PK
МLFKPG – искомое сечение
13.
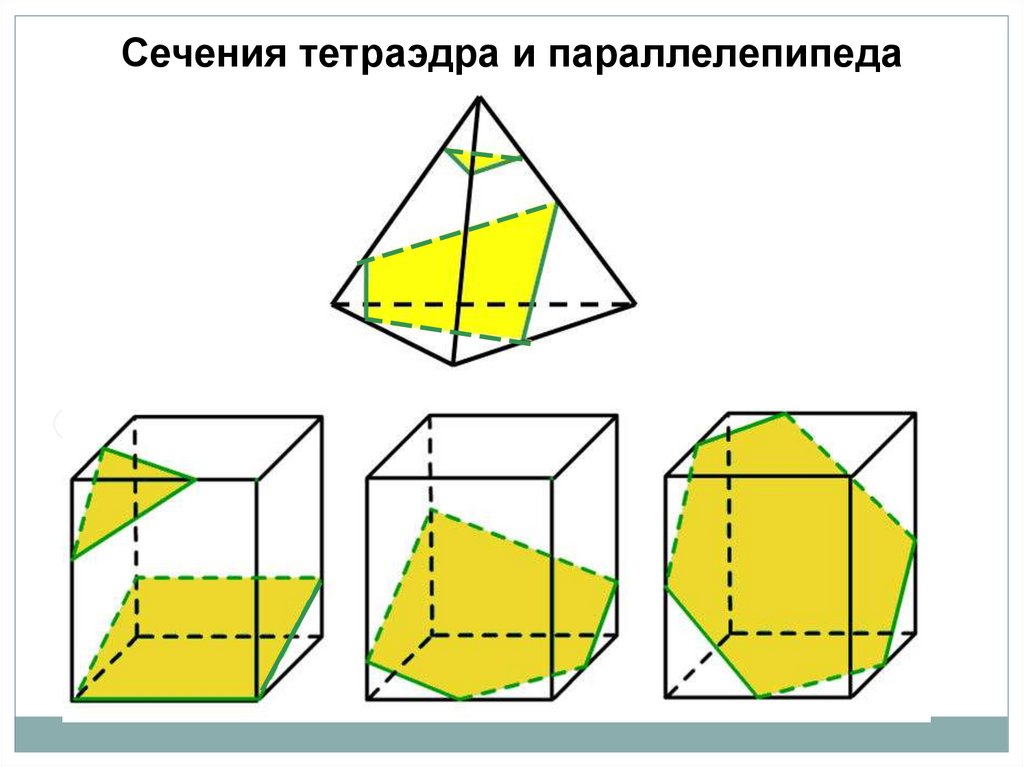
Какие многоугольники могут получиться в сечении ?Тетраэдр имеет 4 грани
В сечениях могут получиться:
Треугольники
Четырехугольники
14.
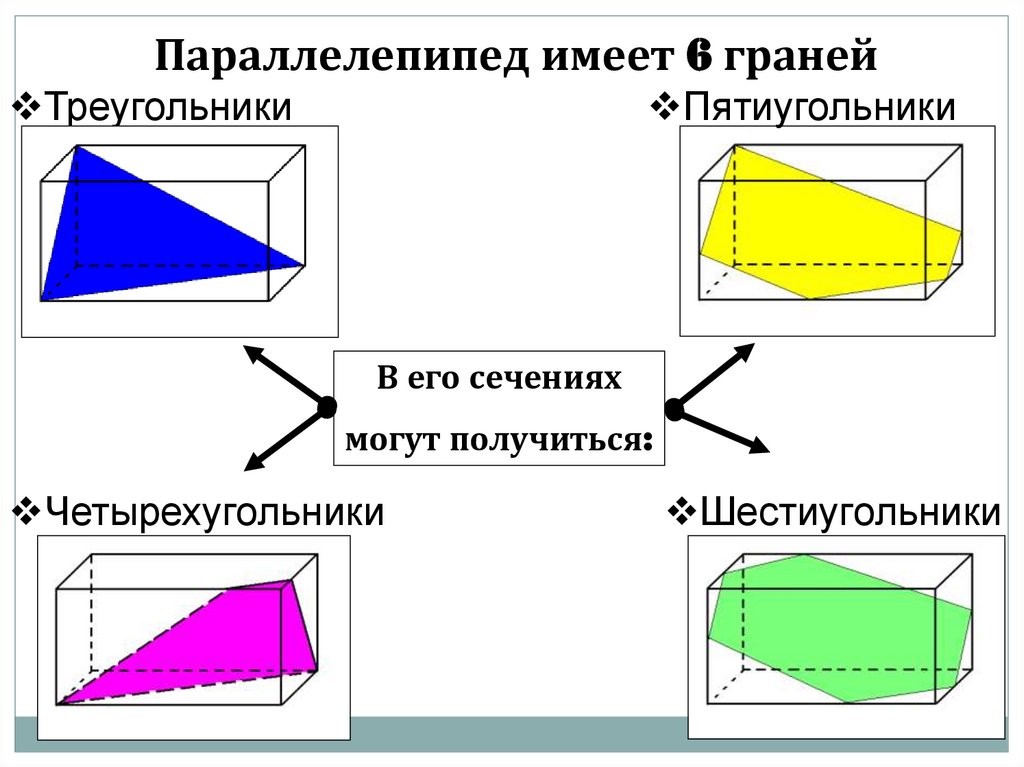
Параллелепипед имеет 6 гранейТреугольники
Пятиугольники
В его сечениях
могут получиться:
Четырехугольники
Шестиугольники
15.
Сечения тетраэдра и параллелепипеда16.
ВЫВОД:Число граней
многогранника
Многогранник
n – число сторон сечения
4
Тетраэдр
3, 4
6
Параллелепипед
3, 4, 5, и 6
Т.к. тетраэдр имеет четыре грани, то в сечении могут
получиться либо треугольники, либо четырехугольники .
Т.к. параллелепипед имеет шесть граней, то в сечении
могут получиться 3,4,5 или 6-угольники.
Следовательно: число сторон сечения зависит
от количества граней многогранника.
17.
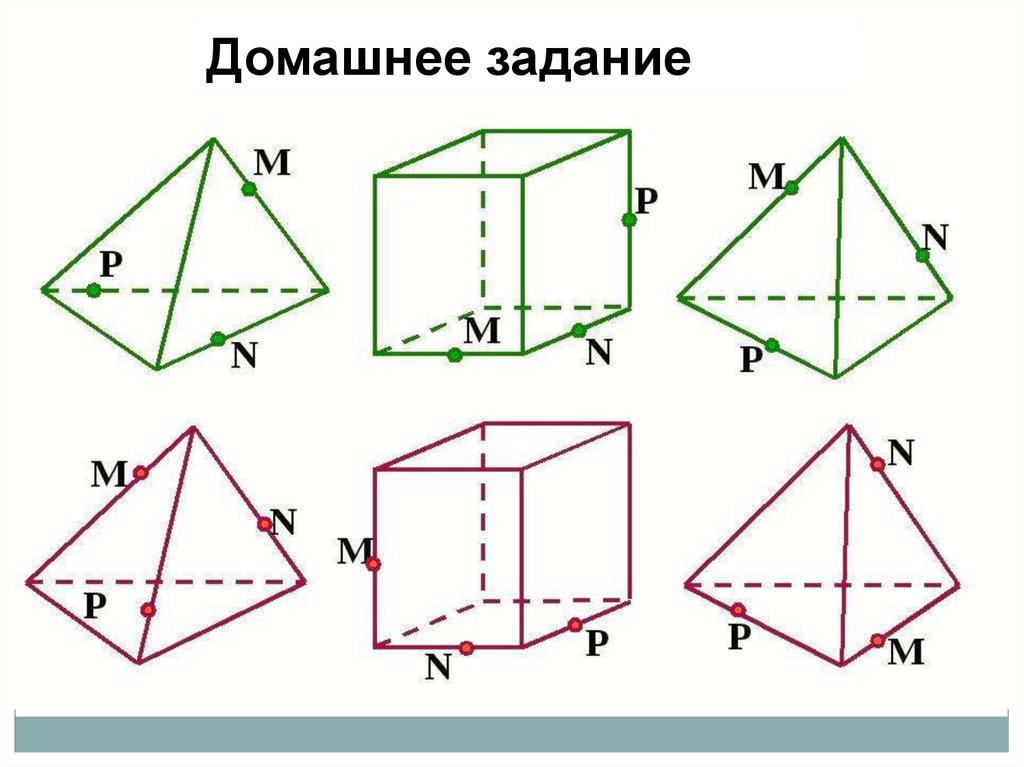
Домашнее задание18.
Итог урока:1.Мне понравился (не понравился) урок, потому что…
2.Сегодня на уроке я научился…
3.Мне хочется, чтобы…
4.В этот урок я добавил бы…___________












 Математика
Математика








