Похожие презентации:
Обратные тригонометрические функции
1.
ОБРАТНЫЕТРИГОНОМЕТРИЧЕСКИЕ
ФУНКЦИИ
2.
Функцииy=arcsinx,y=arccosx,y=arctgx,y=arcctgx
называются обратными
тригонометрическими функциями.
Приставка «arc» означает обратный.
3.
4.
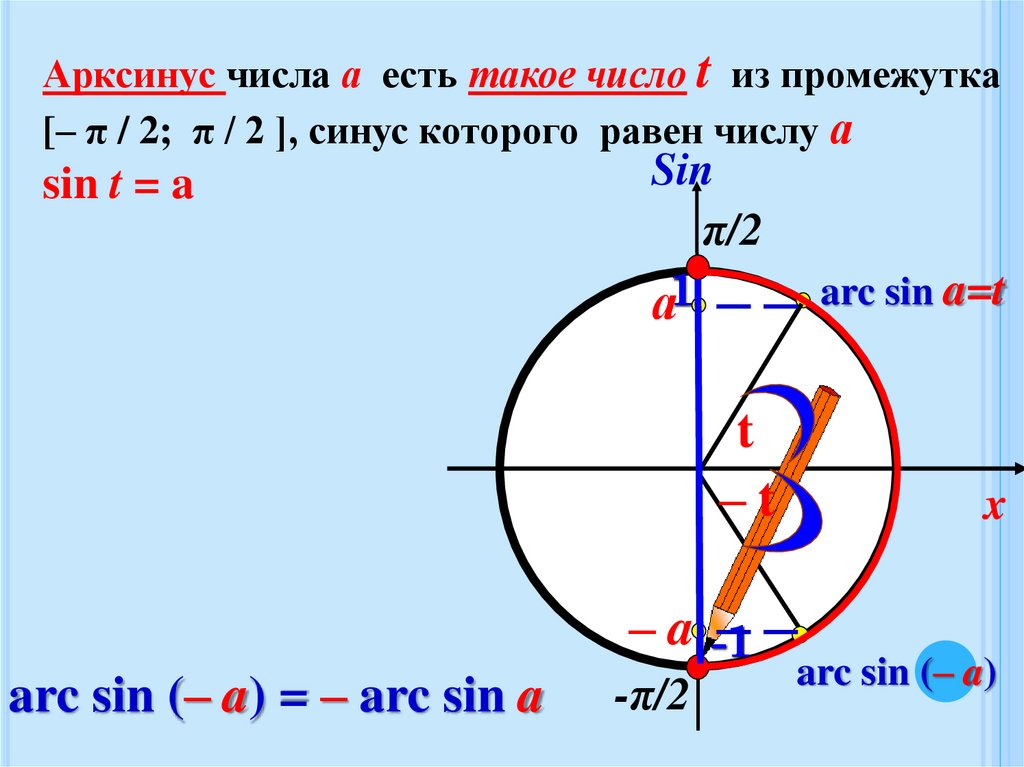
Арксинус числа а есть такое число t из промежутка[– π / 2; π / 2 ], синус которого равен числу а
sin t = a
Sin
π/2
а1
t
–t
– a -1
arc sin (– a) = – arc sin a
-π/2
arc sin a=t
x
arc sin (– a)
5.
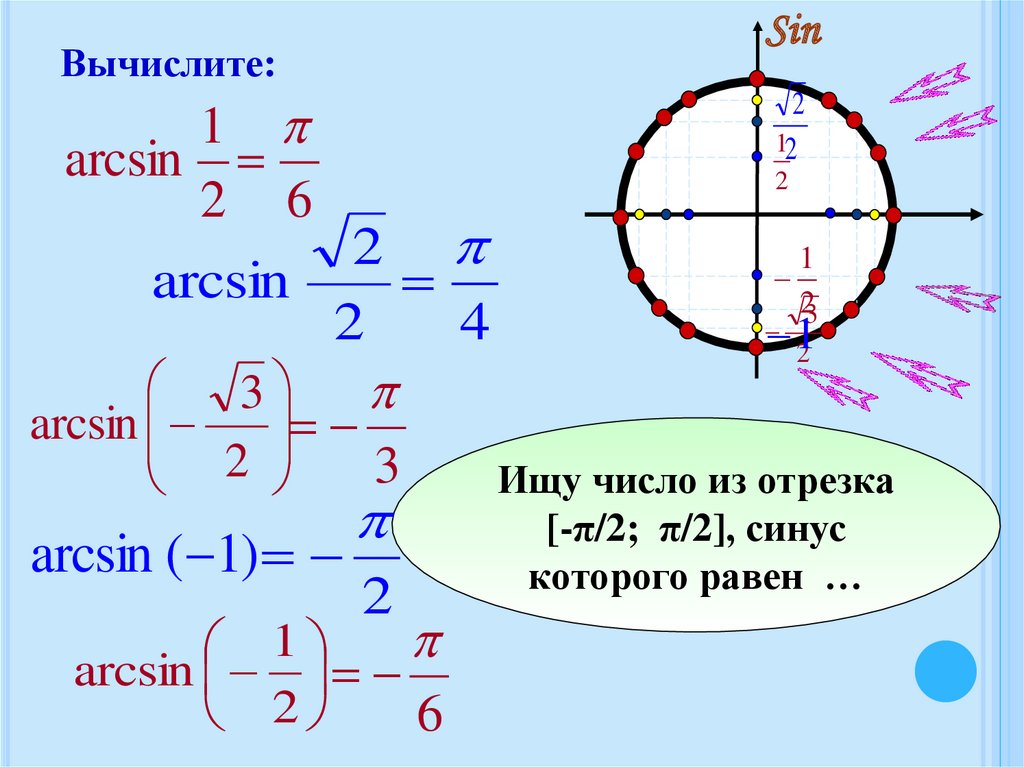
SinВычислите:
1
arcsin
2 6
2
12
2
2
1
arcsin
23
4
2
1
2
3
arcsin
2
3
Ищу число из отрезка
arcsin ( 1)
2
1
arcsin
2
6
[-π/2; π/2], синус
которого равен …
6.
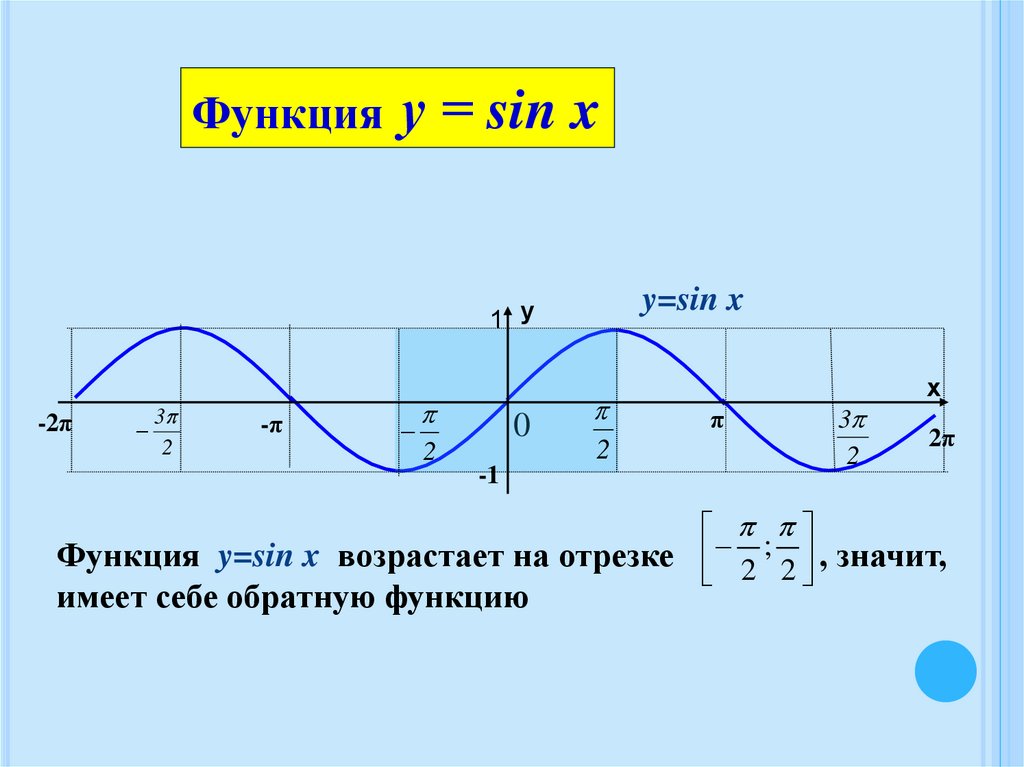
Функцияу = sin x
y=sin x
1 у
-2π
3
2
-π
2
0
-1
2
π
3
2
х
2π
Функция y=sin x возрастает на отрезке 2 ; 2 , значит,
имеет себе обратную функцию
7.
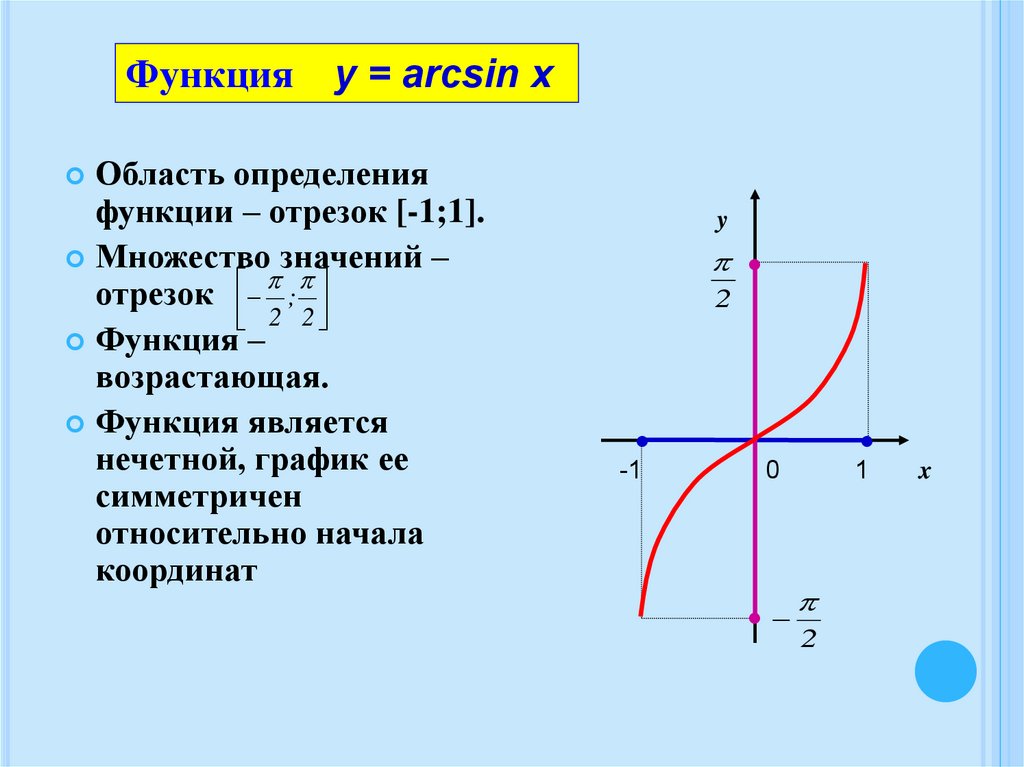
Функцияy = arcsin x
Область определения
функции – отрезок [-1;1].
Множество значений –
отрезок ;
2 2
Функция –
возрастающая.
Функция является
нечетной, график ее
симметричен
относительно начала
координат
y
2
-1
•1
0
2
x
8.
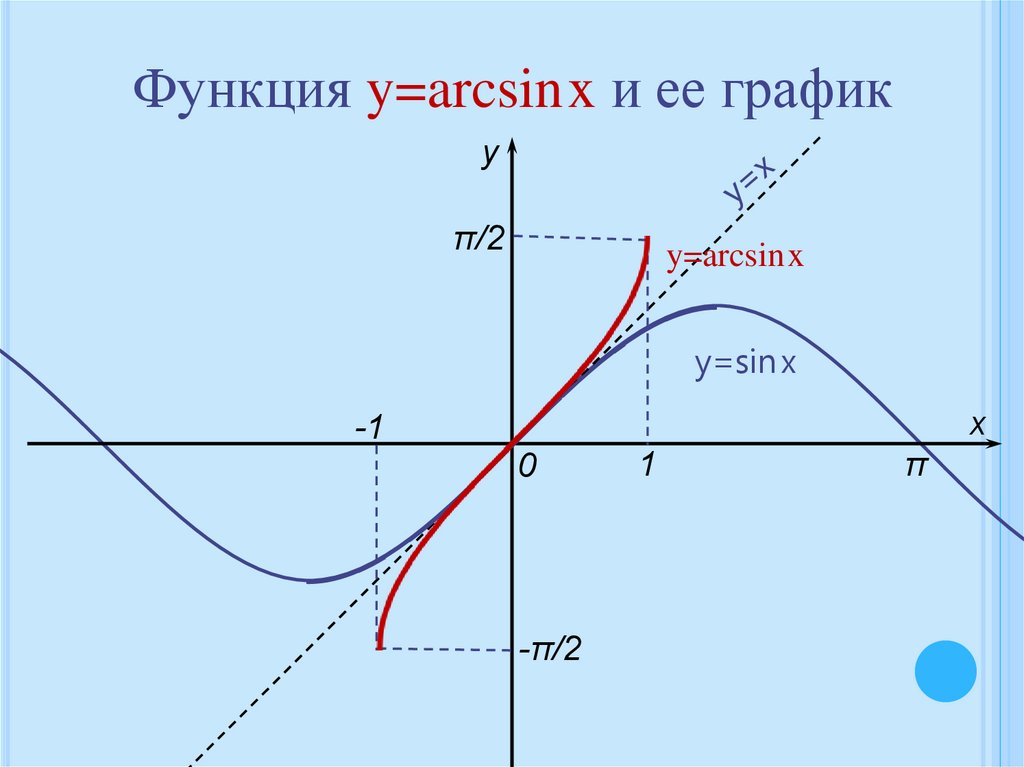
Функция y=arcsinx и ее графику
π/2
y=arcsinx
y=sin x
х
-1
0
-π/2
1
π
9.
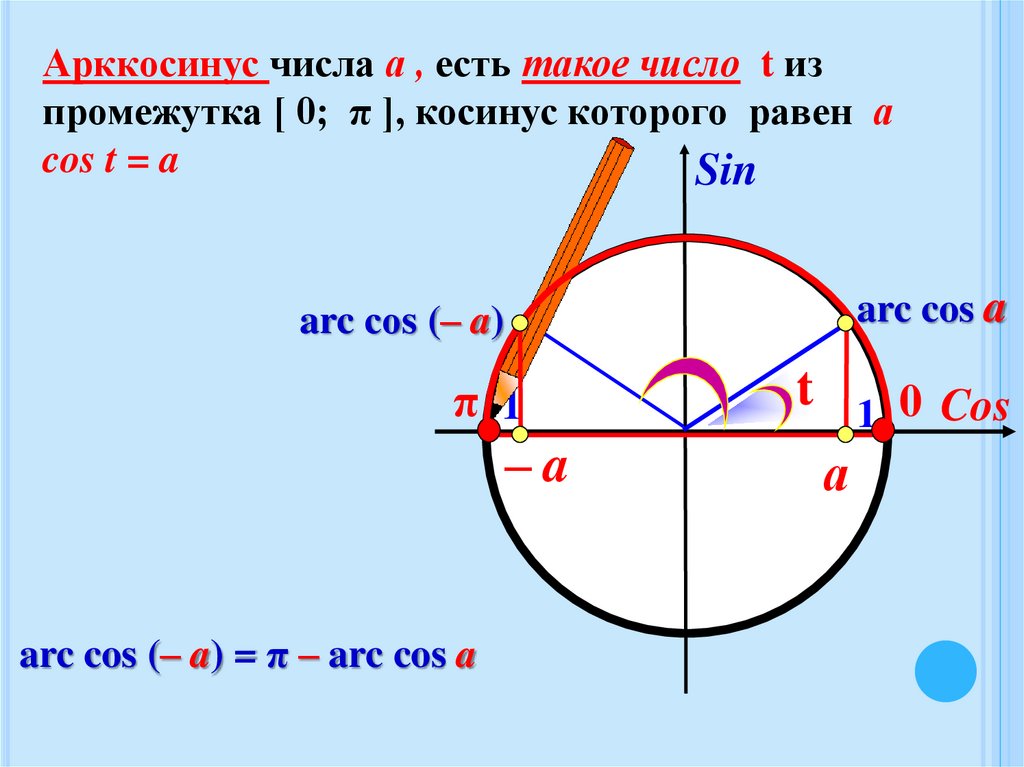
Арккосинус числа а , есть такое число t изпромежутка [ 0; π ], косинус которого равен а
cos t = a
Sin
arc cos a
arc соs (– a)
π -1
–a
arc cos (– a) = π – arc cos a
t
1 0 Cos
а
10.
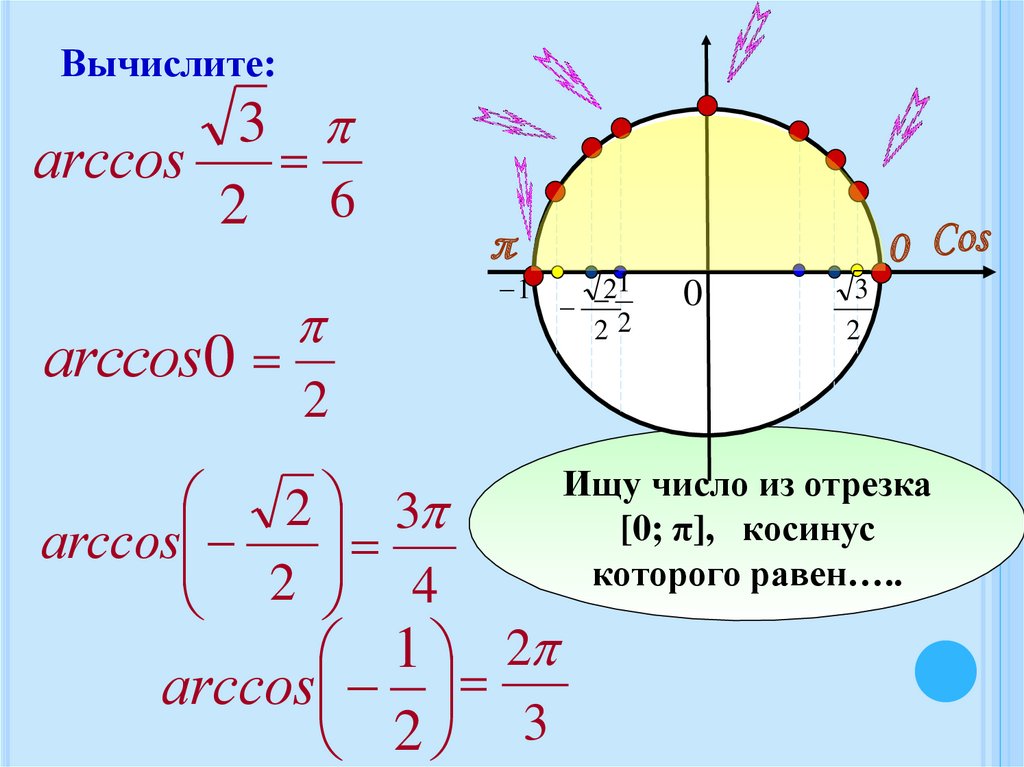
Вычислите:3
arcсos
2 6
arcсos0
2
2 3
arcсos
4
2
0 Cos
π
1
1 2
arcсos
2 3
21
22
0
3
2
Ищу число из отрезка
[0; π], косинус
которого равен…..
11.
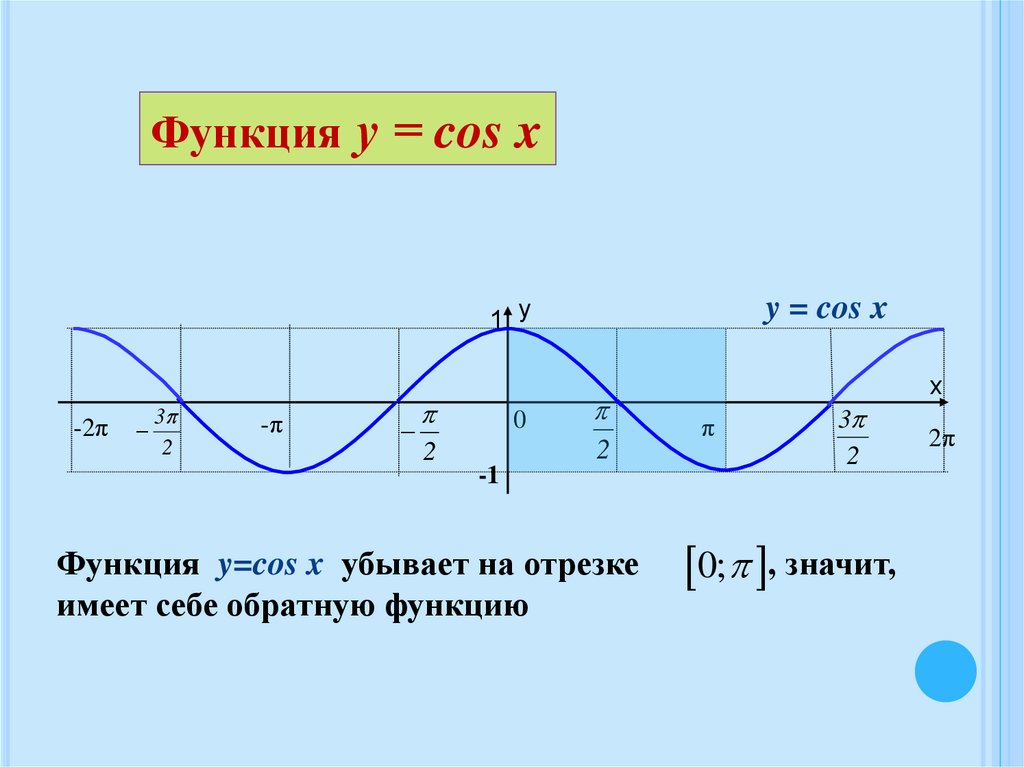
Функция у = cos x1 у
-2π
3
2
-π
2
0
y = cos x
2
-1
Функция y=cos x убывает на отрезке
имеет себе обратную функцию
х
π
3
2
0; , значит,
2π
12.
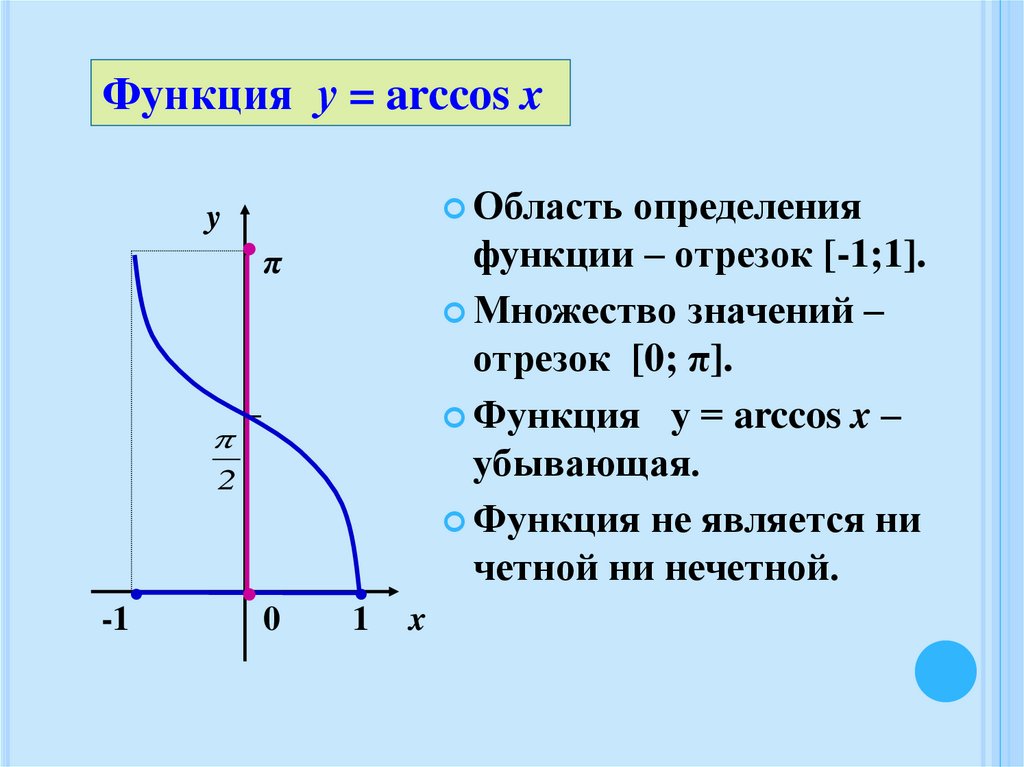
Функция у = arccos xОбласть
определения
функции – отрезок [-1;1].
Множество значений –
отрезок [0; π].
Функция у = arccos x –
убывающая.
Функция не является ни
четной ни нечетной.
y
π
_
2
-1
0
1
x
13.
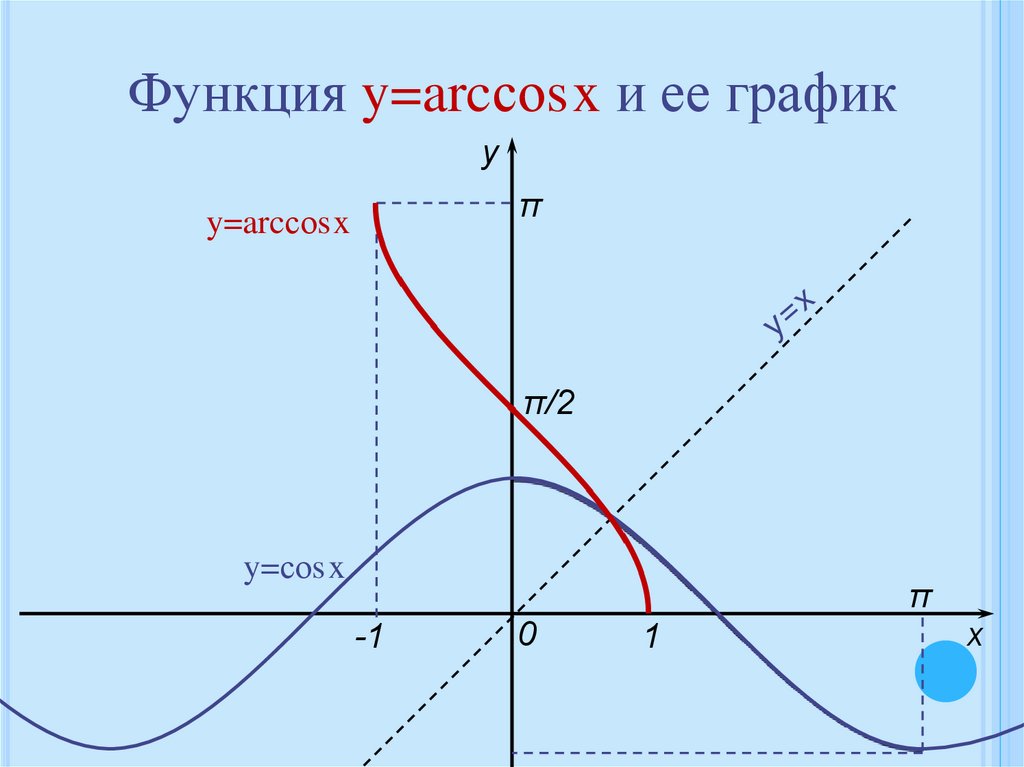
Функция y=arcсоsx и ее графику
π
y=arcсоsx
π/2
y=соsx
π
-1
0
1
х
14.
π1
= 6
arcsin
2
3
π
arcsin
=
2
3 ОТВЕТЫ
π
1
arcsin ( - 2 ) = - 6
π
arcsin 1 =
2
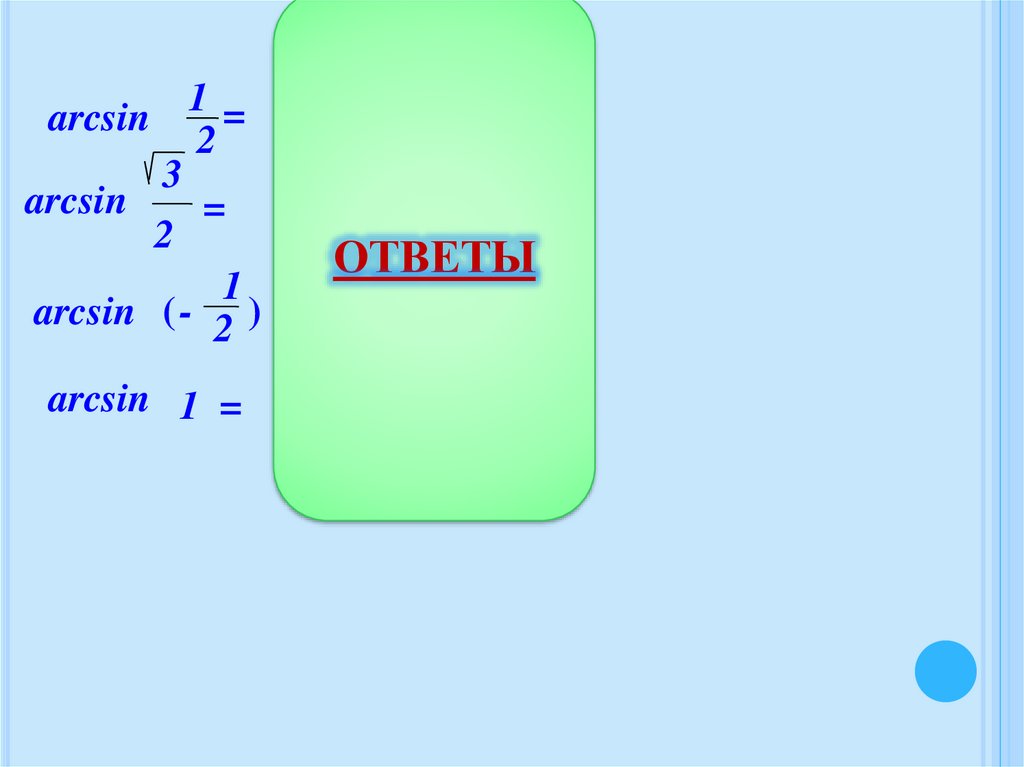
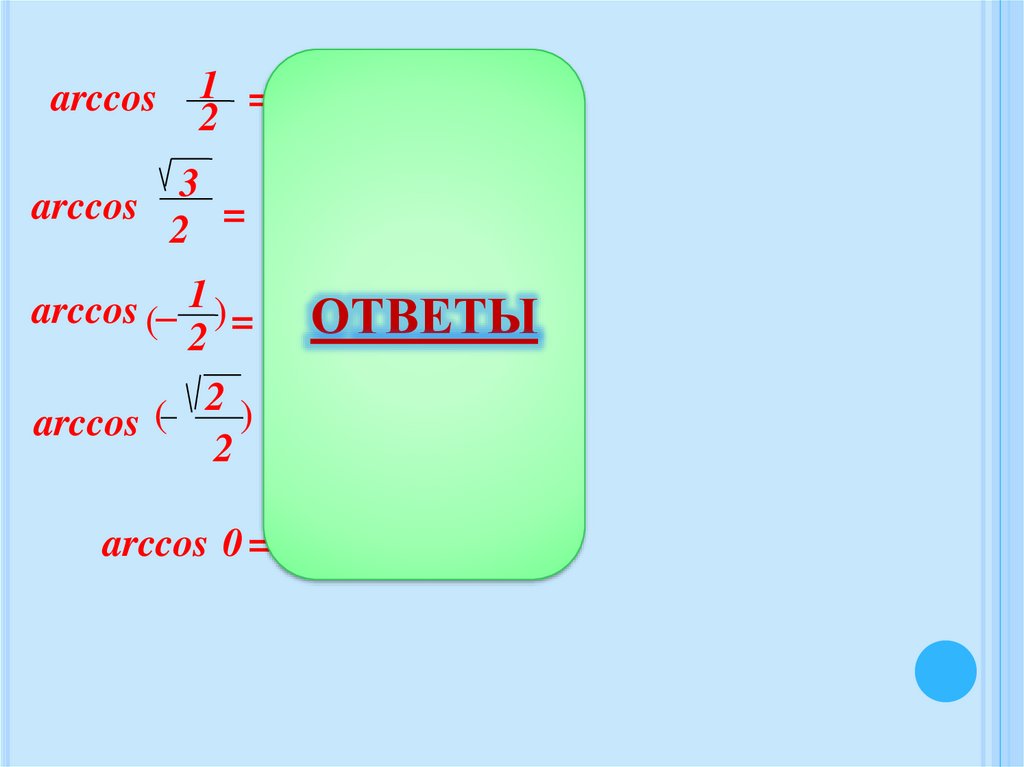
15.
arccos1 = π
2
3
π
3
arccos
2 = 6
1 2π
arccos (− 1 ) = π ̶ ОТВЕТЫ
arccos =
2
2
3
2 ) 3π
(
arccos
=
2
4
arccos 0 =
π
2
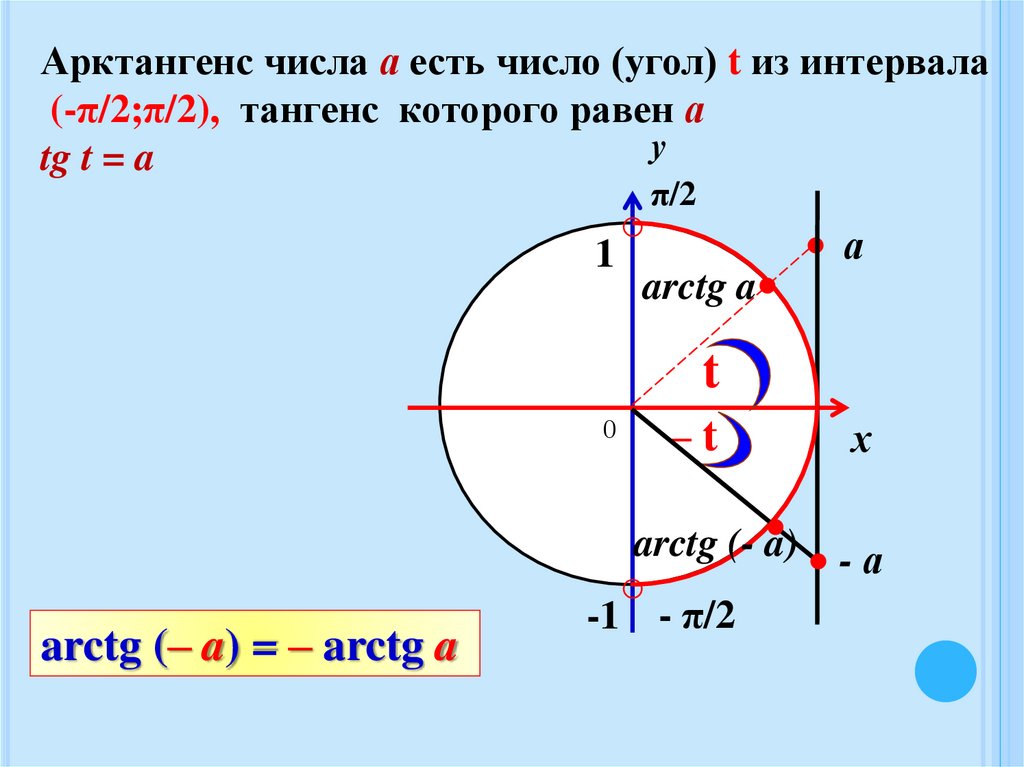
16.
Арктангенс числа а есть число (угол) t из интервала(-π/2;π/2), тангенс которого равен а
у
tg t = a
1
○
π/2
а
arctg a
t
–t
0
arctg (- a)
○
arctg (– a) = – arctg a
-1 - π/2
х
-а
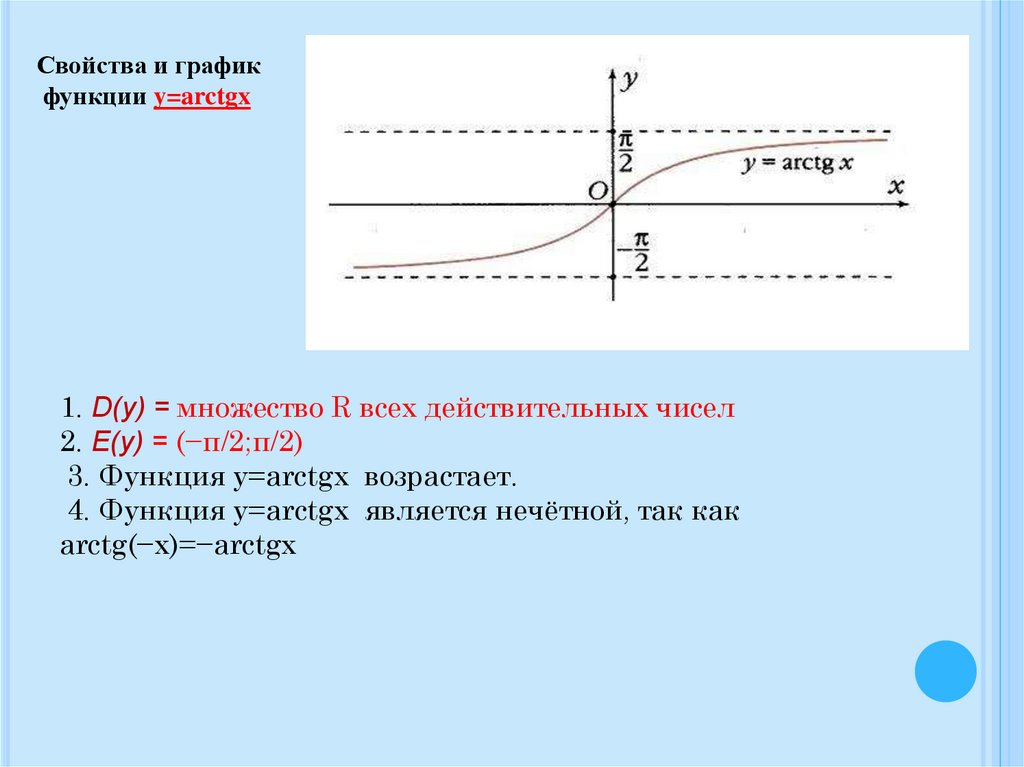
17.
Свойства и графикфункции y=arctgx
1. D(y) = множество R всех действительных чисел
2. E(y) = (−π/2;π/2)
3. Функция y=arctgx возрастает.
4. Функция y=arctgx является нечётной, так как
arctg(−x)=−arctgx
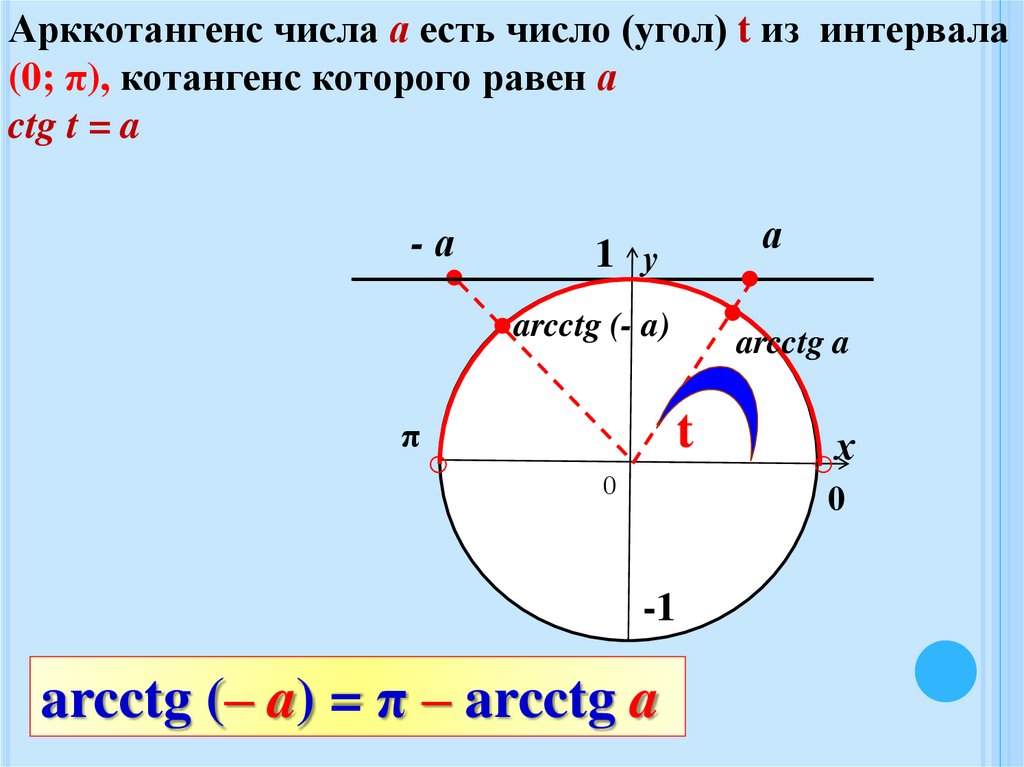
18.
Арккотангенс числа а есть число (угол) t из интервала(0; π), котангенс которого равен а
ctg t = a
-а
а
1 у
arcctg (- a)
π
○
arcctg a
t
0
○х
0
-1
arcctg (– a) = π – arcctg a
19.
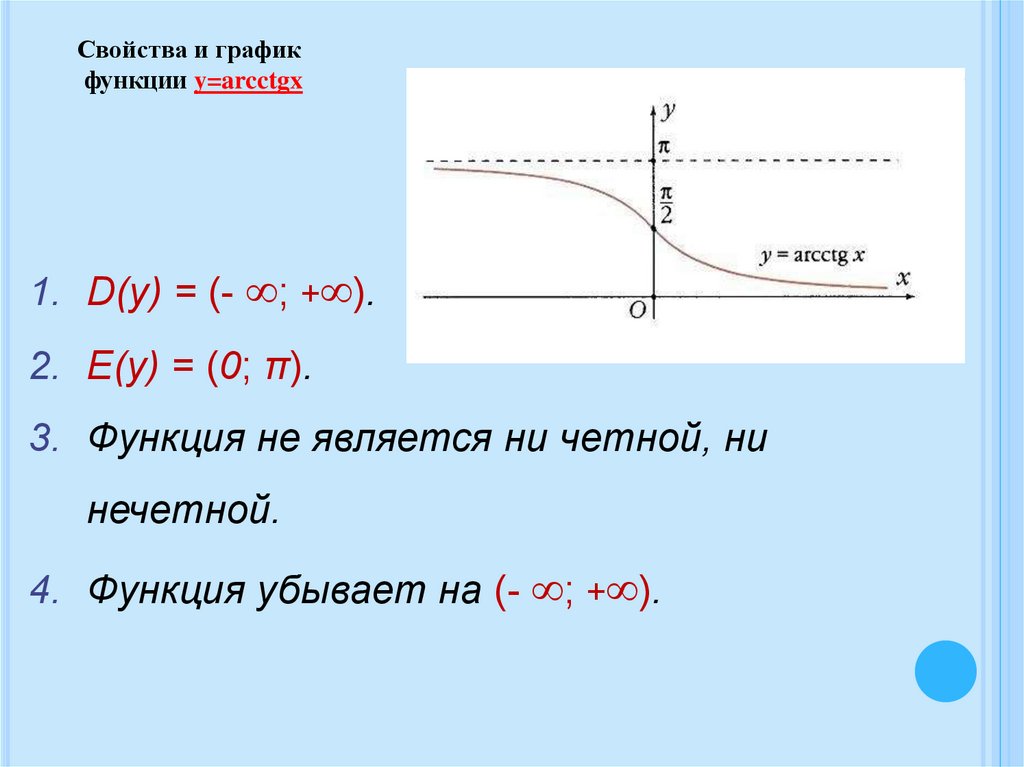
Свойства и графикфункции y=arcctgx
1. D(y) = (- ; + ).
2. E(y) = (0; π).
3. Функция не является ни четной, ни
нечетной.
4. Функция убывает на (- ; + ).
20.
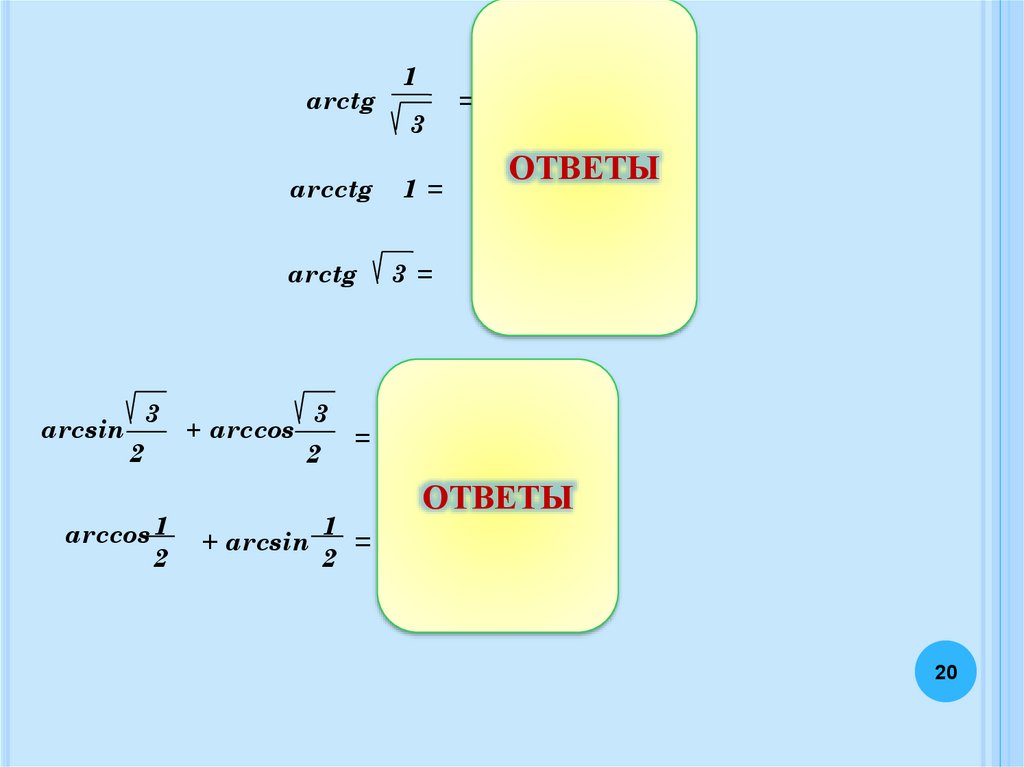
arсtgarсctg
arсtg
arcsin
3
2
arccos 1
2
+ arccos
3
2
=
1
3
1=
3=
=
П
6
ОТВЕТЫ
П
4
П
3
П
П
П
+ 6 =
2
3
ОТВЕТЫ
+ arcsin
1
= П + П = П
2
6
2
3
20
21.
22.
ДОМАШНЕЕ ЗАДАНИЕВычислить:




 Математика
Математика








