Зеркальная симметрия

1.

«Симметрия, как бы широко или узко мы
ни понимали это слово, есть идея с
помощью которой человек веками
пытался объяснить и создать порядок,
Красоту и совершенство»
( Герман Вейль)
Презентация ученицы 11 класса А,
гимназии № 65 Трясцыной Марии.

2. СИММЕ́ТРИ́Я, в геометрии — свойство геометрических фигур. Две точки, лежащие на одном перпендикуляре

СИММЕ́ТРИ́Я, в геометрии —
свойство геометрических фигур. Две точки, лежащие на одно
м перпендикуляре
к данной плоскости (или прямой) по разные стороны и на один
аковом расстоянии от нее, называются
симметричными относительно этой плоскости (или прямой). Ф
игура (плоская или пространственная)симметрична относитель
но прямой (оси симметрии) или плоскости (плоскости симметр
ии), если ее точки
попарно обладают указанным свойством. Фигура симметрична
относительно точки (центр симметрии), если ее
точки попарно лежат на прямых, проходящих через центр сим
метрии, по разные стороны и на равных расстояниях от него.

3. Зеркальная симметрия

Математическое понятие соотношение в
оптике объектов и их (мнимых) изображений
при отражении в плоском зеркале , а также
многие законы симметрии.

4. Зеркальная симметрия.

Зеркальная симметрия хорошо знакома
каждому человеку из повседневного
наблюдения. Как показывает само
название, зеркальная симметрия
связывает любой предмет и его
отражение в плоском зеркале. Говорят,
что одна фигура (или тело) зеркально
симметрично другой, если вместе они
образуют зеркально симметричную
фигуру (или тело).

5. Определение

Зеркальной симметрией (симметрией относительно плоскости
) называется такое отображение пространства на себя,
при котором любая точка М переходит в симметричную ей
относительно этой плоскости точку М1.
М
ММ
М
м
М
К
К
ОО
К1
М1М
ОМ=ОМ1 ; ММ1
М1
МК=М1К1

6. Фигуры, симметричные относительно плоскости

Фигура ( тело) называется симметричной относительно
некоторой плоскости, если эта плоскость разбивает фигуру
на две равные симметричные части.

7.

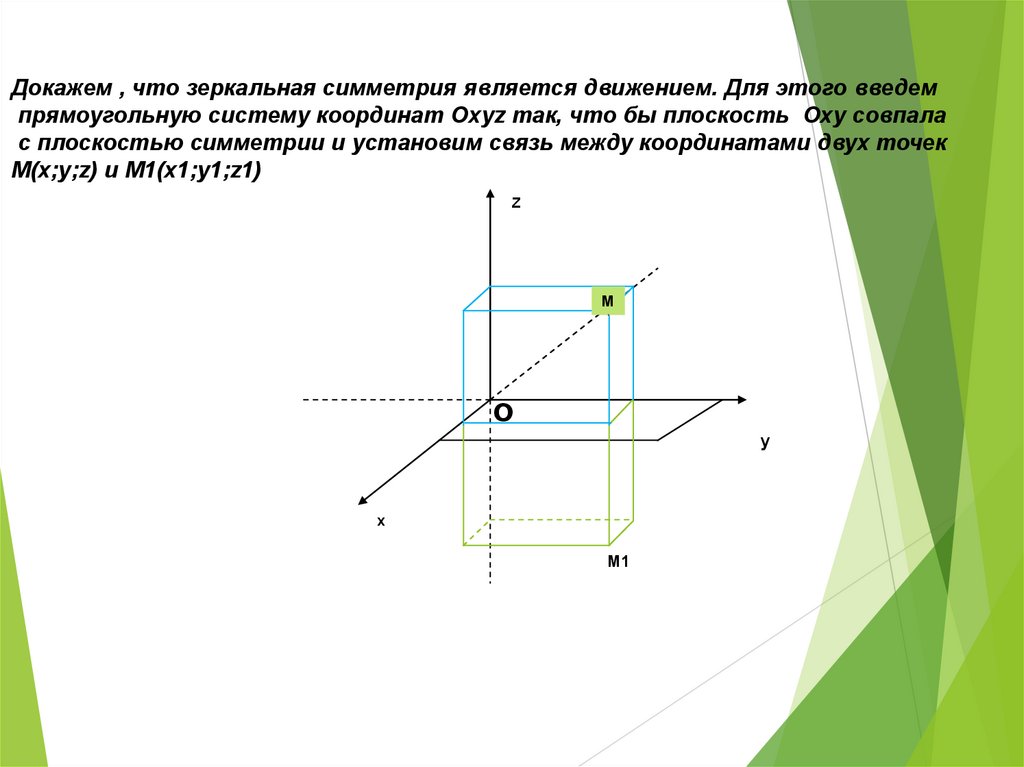
Докажем , что зеркальная симметрия является движением. Для этого введем
прямоугольную систему координат Oxyz так, что бы плоскость Oxy совпала
с плоскостью симметрии и установим связь между координатами двух точек
М(x;y;z) и М1(x1;y1;z1)
Z
М
о
y
x
М1

8.

9. Зеркальная симметрия в архитектуре и природе.

Отражение прибрежных зданий
Оптическое отражение в реке
прибрежных деревьев
Отражение свечи в зеркале

10.

Спасибо за просмотр!