Преобразование тригонометрических выражений

1. Преобразование тригонометрических выражений

Формулы
Тригонометрии

2. Содержание

Зависимость между синусом, косинусом, тангенсом и
котангенсом одного и того же угла
Синус и косинус суммы и разности
Тангенс суммы и разности
Формулы приведения
Формулы двойного угла
Формулы понижения степени
Преобразование сумм тригонометрических функций
в произведение
Преобразование произведений тригонометрических
функций в суммы
Преобразование выражения Asinx+Bcosx
содержание
ВЫХОД

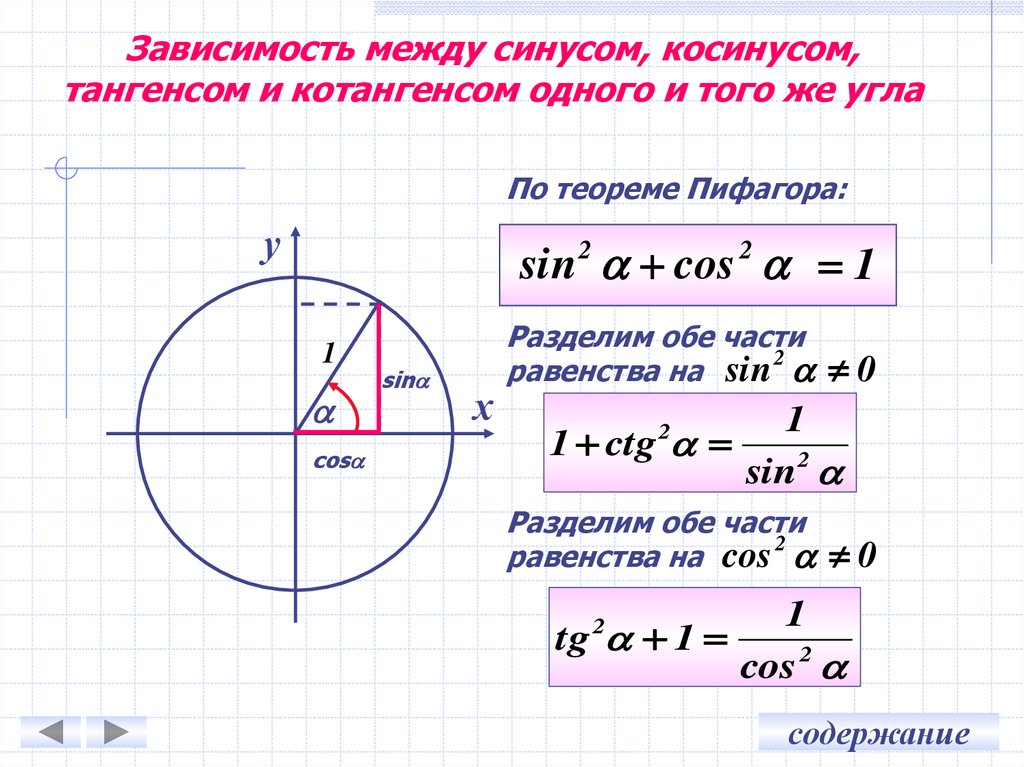
3. Зависимость между синусом, косинусом, тангенсом и котангенсом одного и того же угла

По теореме Пифагора:
у
sin cos 1
2
1
cos
sin
х
2
Разделим обе части
2
равенства на sin 0
1
1 ctg
sin2
2
Разделим обе части
2
равенства на cos 0
1
tg 1
cos 2
2
содержание

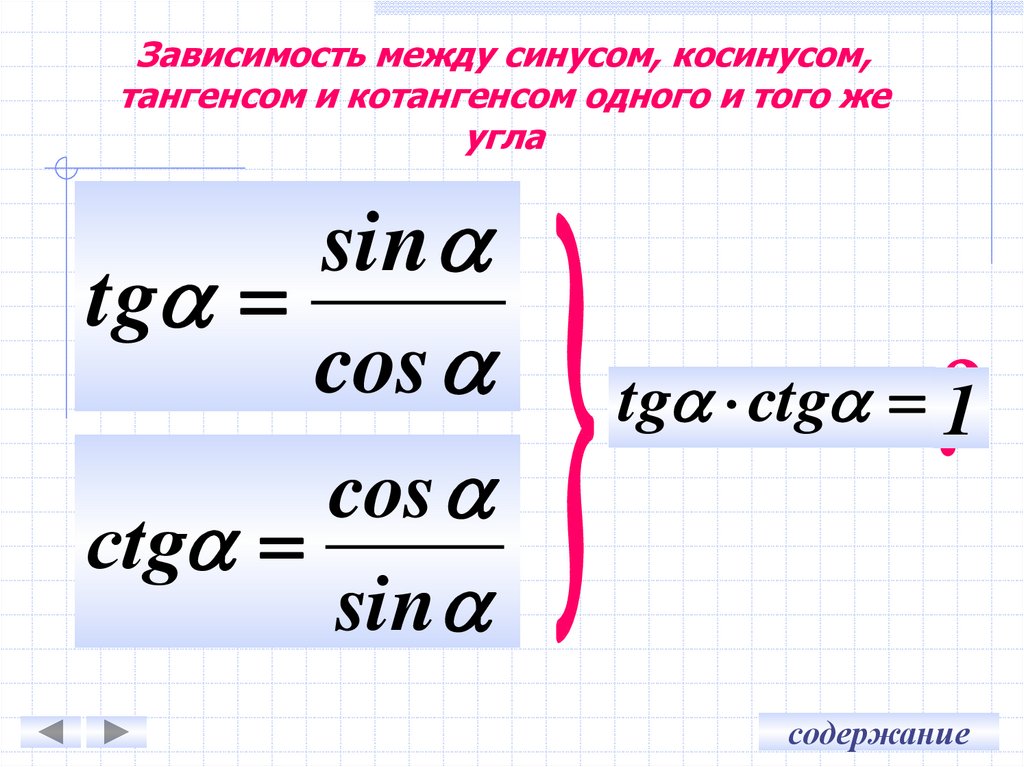
4. Зависимость между синусом, косинусом, тангенсом и котангенсом одного и того же угла

sin
tg
cos
cos
сtg
sin
tg ctg 1
?
содержание

5. Пример 1

sin t
3
и 0 t . Найти cost, tgt, ctgt.
5
2
sin 2 t cos 2 t 1
2
16
3
2
2
cos t 1 sin t 1
25
5
4
4
cos t
или cos t
5
5
4
т.к. 0 t (I четверть, cost 0), то cost
2
5
sin t
tgt
cos t
3 4 3
tgt :
5 5 4
ctgt
4
ctgt
3
содержание
1
tgt

6. Пример 2

5
tgt
и
t . Найти sint, cost, ctgt.
Пример 2
12
2
1
tg t 1
cos 2 t
2
2
1
169
5
1
2
cos t
144
12
12
12
cos t
или cos t
13
13
12
т.к. t (II четверть, cost 0), то cost
2
sin t
tgt
cos t
1
ctgt
tgt
13
5 12 5
sin t tgt cos t
12 13 13
12
ctgt
5
содержание

7. Синус и косинус суммы и разности аргументов

sin x y sin x cos y cos xsin y
sin x y sin x cos y cos xsin y
cos x y cos xcos y
sin xsin y
cos x
y cos xcos y sin x sin y
содержание

8. Синус и косинус суммы и разности аргументов

Решить уравнение : sin x cos x 3
3
6
sin x y sin x cos y cos xsin y
cos x y cos xcos y sin x sin y
sin
cos
x
cos
sin
x
cos
cos
x
sin
sin
x
3
3
3
6
6
у
3
1
3
1
cos x sin x
cos x sin x 3
2
2
2
2
3 cos x 3
0
cos x 1
2 n
х
x 2 n , n Z
Ответ : 2 n , n Z
содержание

9. Тангенс суммы и разности аргументов

tgx tgy
tg x y
1
tgxtgy
tgx tgy
tg x y
1 tgxtgy
содержание

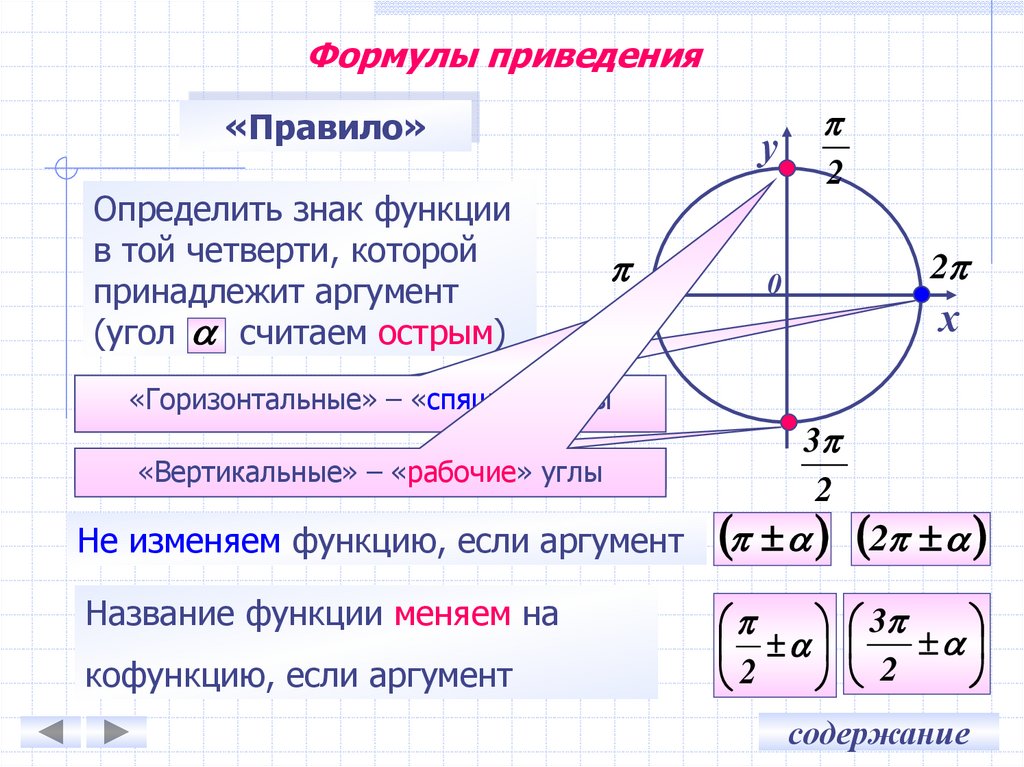
10. Формулы приведения

«Правило»
Определить знак функции
в той четверти, которой
принадлежит аргумент
(угол считаем острым)
у
«Горизонтальные» – «спящие» углы
«Вертикальные» – «рабочие» углы
Не изменяем функцию, если аргумент
Название функции меняем на
кофункцию, если аргумент
2
2
0
х
3
2
2
3
2
2
содержание

11. Формулы двойного угла

sin 2 x sin( x x ) sin x cos x cos x sin x 2 sin x cos x
sin 2 x 2 sin x cos x
cos 2 x cos( x x ) cos x cos x sin x sin x cos 2 x sin2 x
cos 2 x cos x sin x
2
2
tgx tgx
2 tgx
tg 2 x tg( x x )
1 tgxtgx 1 tg 2 x
2 tgx
tg 2 x
1 tg 2 x
содержание

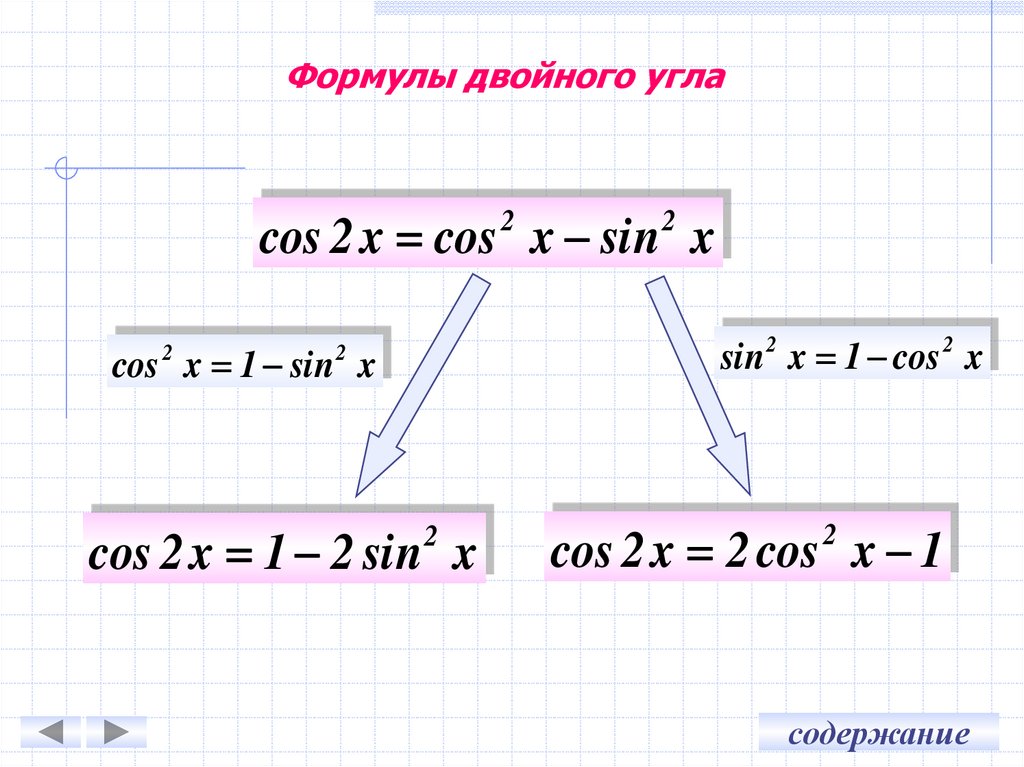
12. Формулы двойного угла

cos 2 x cos x sin x
2
sin 2 x 1 cos 2 x
cos x 1 sin x
2
2
2
cos 2 x 1 2 sin x
2
cos 2 x 2 cos x 1
2
содержание

13. Формулы понижения степени

cos 2 x 1 2 sin x
cos 2 x 2 cos x 1
Выразим
Выразим
2
sin2 x
1 cos 2 x
sin x
2
2
2
cos 2 x
1 cos 2 x
cos x
2
2
содержание

14. Преобразование сумм тригонометрических функций в произведение

x y
x y
cos
sin x sin y 2 sin
2
2
x y
x y
cos
sin x sin y 2 sin
2
2
cos x cos y 2 cos
x y
x y
cos
2
2
x y
x y
cos x cos y 2sin
sin
2
2
содержание

15. Преобразование суммы тригонометрических функций в произведение

Решите уравнение: sin17x=sin7x
sin 17 x sin7 x 0
Применим формулу
sin x sin y 2 sin
x y
x y
cos
2
2
2 sin 5 x cos 12 x 0
sin 5 x 0
5 x n , n Z
Ответ:
x
n
5
,n Z
или
cos12 x 0
12 x n , n Z
2
n
x
,n Z
24 12
содержание

16. Преобразование произведений тригонометрических функций в суммы

1
cos x cos y cos x y cos x y
2
1
sin x sin y cos x y cos x y
2
1
sin x cos x sin x y sin x y
2
содержание

17. Преобразование выражения Asinx+Bcosx

a
b
a sin x b cos x a b
sin x
cos x
2
2
a 2 b2
a b
2
2
a 2 b 2 cos t sin x sin t cos x a 2 b 2 sin( x t )
a
cos t
,
2
2
b
b
a b
tgt , t arctg
a
a
b
sin t
.
2
2
a b
b
a sin x b cos x a b sin x arctg
a
2
2
содержание

18. Преобразование выражения Asinx+Bcosx

b
a sin x b cos x a b sin x arctg
a
2
2
Найдите наибольшее и наименьшее значение функции
y 5 sin x 12 cos x
12
y 13 sin x arctg
Применим формулу:
5
y 13 sin x arctg2 ,4
т .к . - 1 sin 1, yнаим 13 , yнаиб 13.
Ответ : yнаим 13 , yнаиб 13.
содержание