Тетраэдр. Тест

1.

Тетраэдр

2.

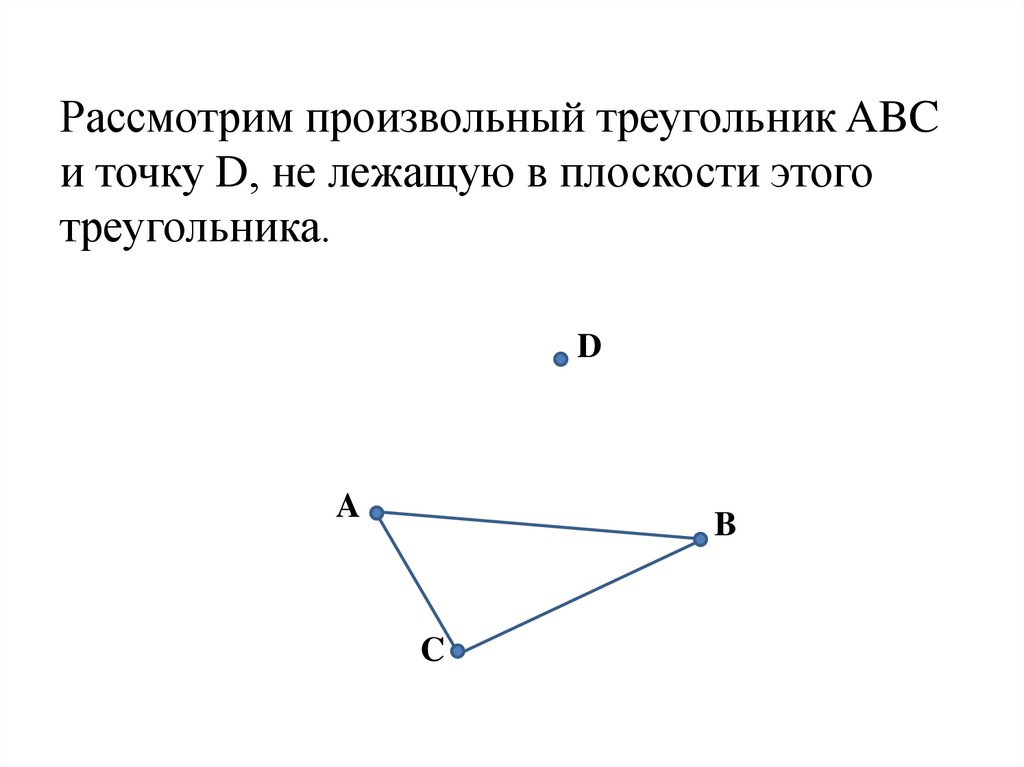
Рассмотрим произвольный треугольник ABC
и точку D, не лежащую в плоскости этого
треугольника.
D
A
B
C

3.

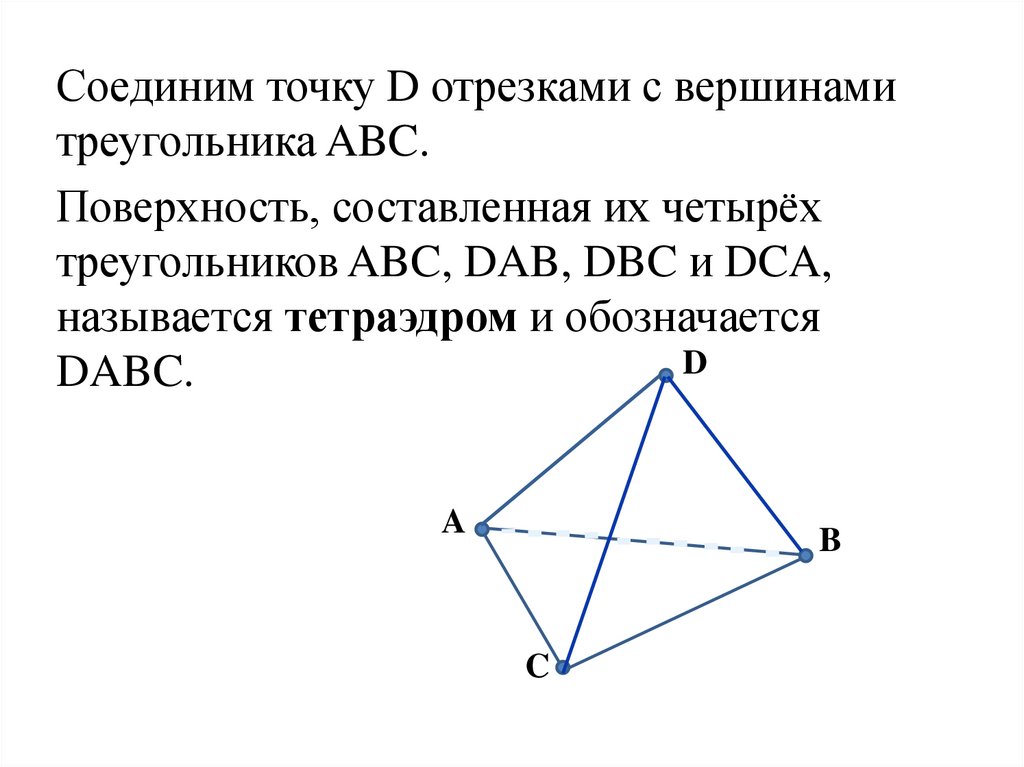
Соединим точку D отрезками с вершинами
треугольника ABC.
Поверхность, составленная их четырёх
треугольников ABC, DAB, DBC и DCA,
называется тетраэдром и обозначается
D
DABC.
A
B
C

4.

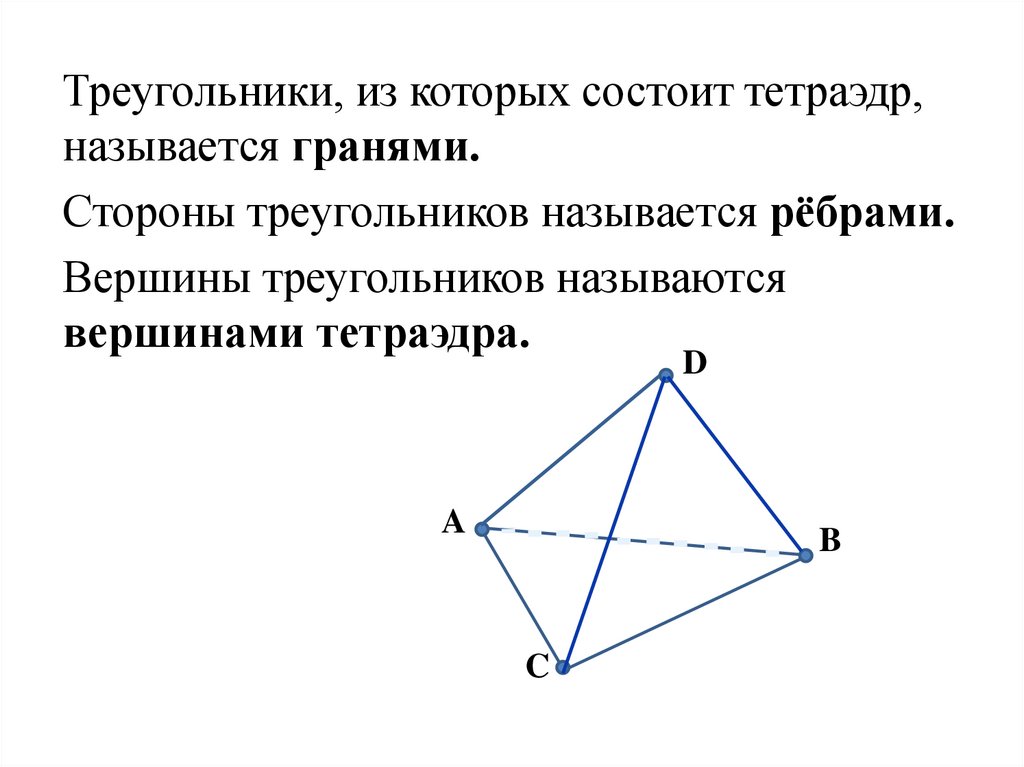
Треугольники, из которых состоит тетраэдр,
называется гранями.
Стороны треугольников называется рёбрами.
Вершины треугольников называются
вершинами тетраэдра.
D
A
B
C

5.

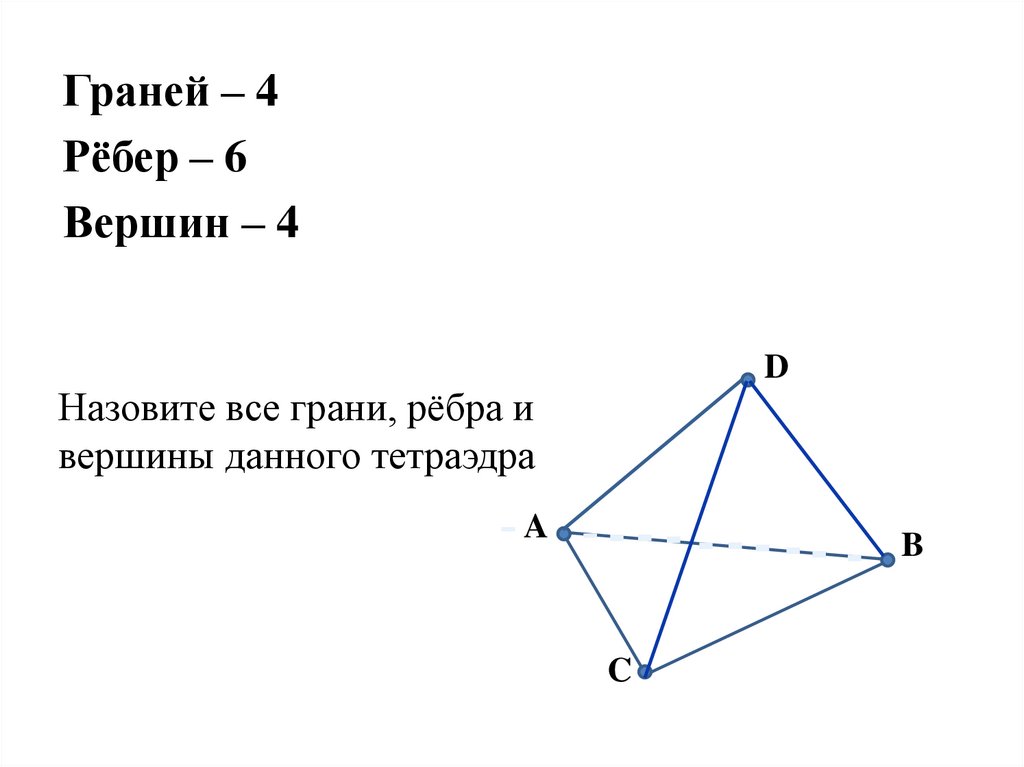
Граней – 4
Рёбер – 6
Вершин – 4
D
Назовите все грани, рёбра и
вершины данного тетраэдра
A
B
C

6.

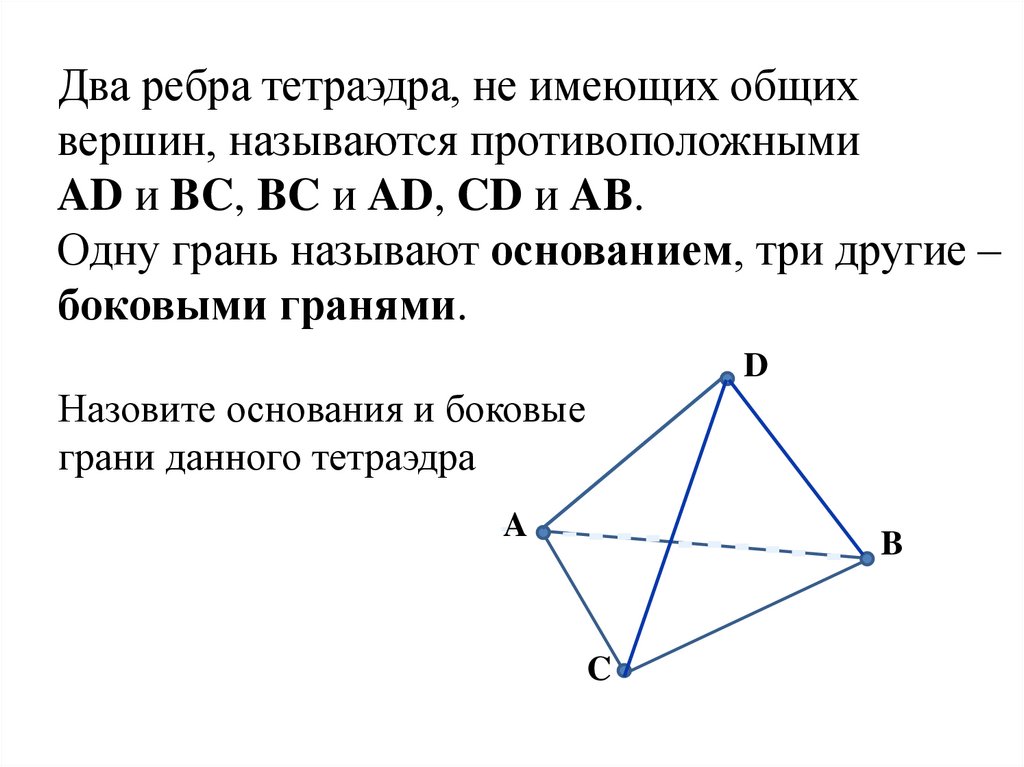
Два ребра тетраэдра, не имеющих общих
вершин, называютcя противоположными
AD и BC, BC и AD, CD и AB.
Одну грань называют основанием, три другие –
боковыми гранями.
D
Назовите основания и боковые
грани данного тетраэдра
A
B
C

7.

Решите задачу
В тетраэдре DАВС угол АDВ = 300, угол
ВDС = 600, угол СDА = 900, DА = 20 см,
ВD = 21 см, DС = 18 см. Найдите площади
всех боковых граней.

8.

Тест
Тетраэдр - поверхность, составленная из…
А) 4 треугольников
Б) 3 треугольников
В) 5 треугольников
Г) 4 четырехугольников

9.

Тест
Концы ребер многоугольника называют….
А) грани
Б) ребра
В) вершины
Г) диагонали

10.

Тест
Гранями тетраэдра являются:
А) отрезки;
Б) четырехугольники;
В) треугольники;
Г) прямые.

11.

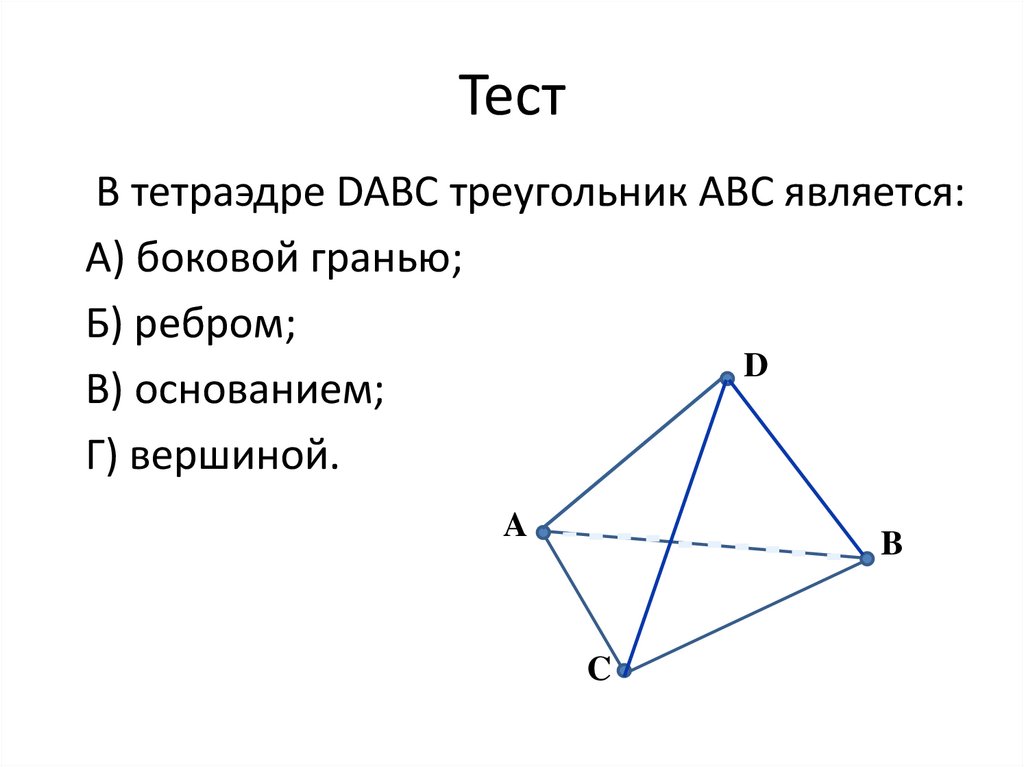
Тест
В тетраэдре DABC треугольник ABC является:
А) боковой гранью;
Б) ребром;
D
В) основанием;
Г) вершиной.
A
B
C

12.

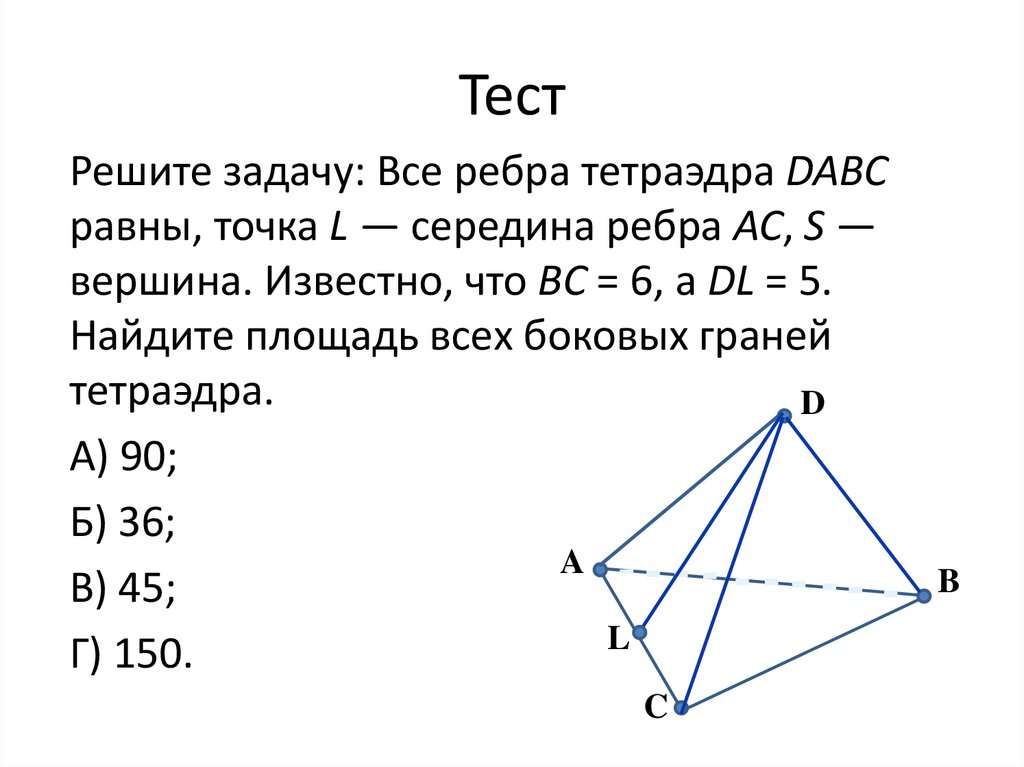
Тест
Решите задачу: Все ребра тетраэдра DABC
равны, точка L — середина ребра AC, S —
вершина. Известно, что BC = 6, а DL = 5.
Найдите площадь всех боковых граней
тетраэдра.
D
А) 90;
Б) 36;
A
В) 45;
L
Г) 150.
C
B