Похожие презентации:
Многогранники. Тетраэдр
1. ТЕТРАЭДР
2.
— тетра-пакет длямолока
3.
— горка измандаринов
4.
— четырёхсторонняяигральная кость
5.
ТЕТРА́ ЭДР [фр. tétraèdre <греч. tetra четыре + hedra
сторона, основание]. геом. –
четырёхгранник,
треугольная пирамида
Kjell André
6.
План изучениямногогранников:
— определение тетраэдра
— элементы тетраэдра
— развёртка тетраэдра
— изображение на плоскости
7.
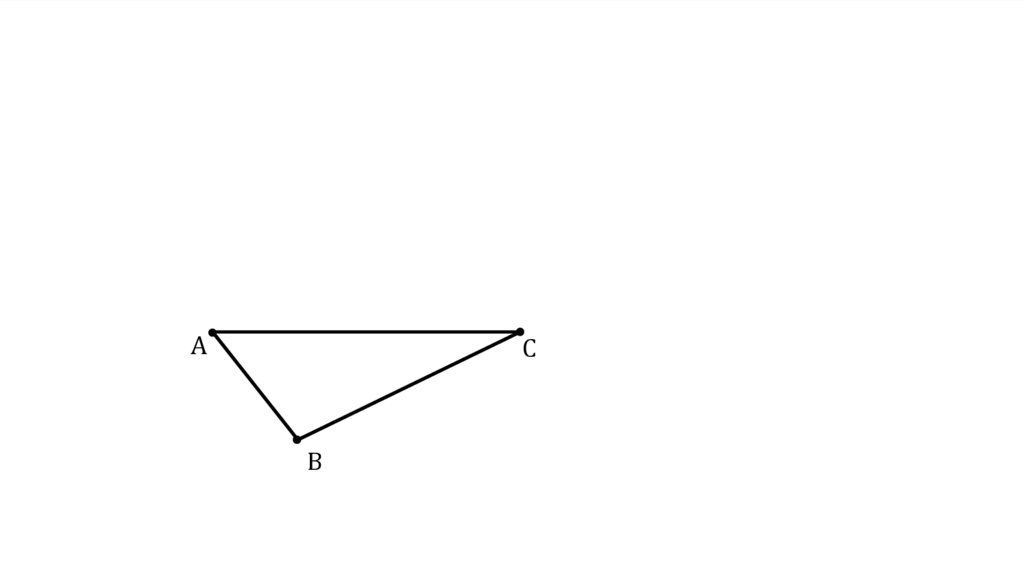
AC
B
8.
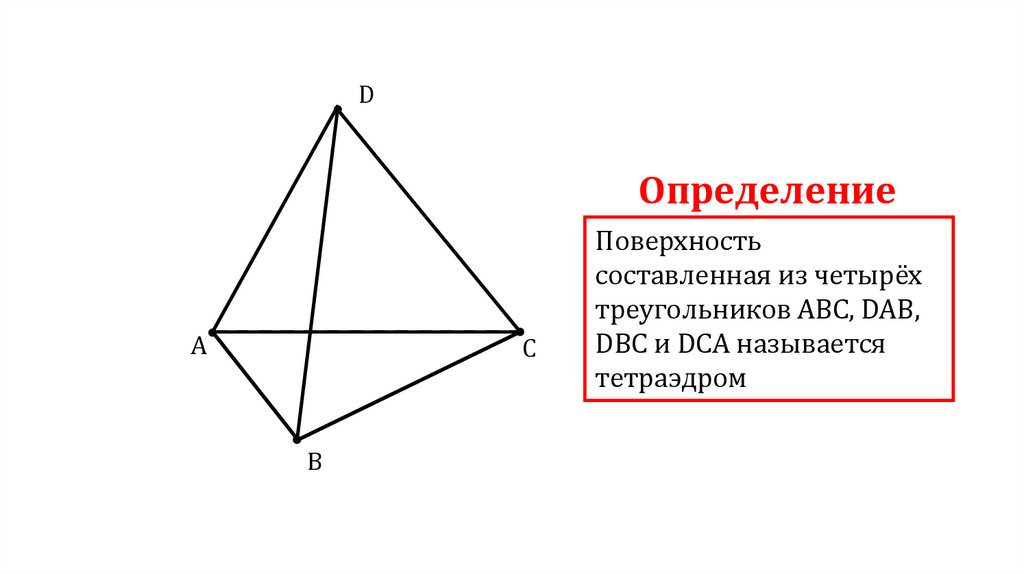
DОпределение
A
C
B
Поверхность
составленная из четырёх
треугольников АBC, DAB,
DBC и DCA называется
тетраэдром
9.
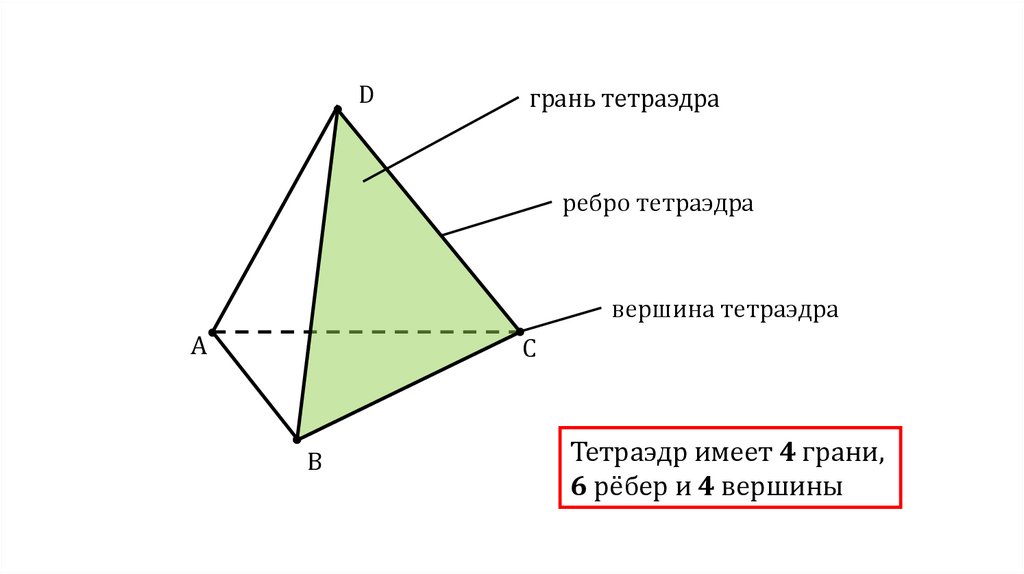
Dгрань тетраэдра
ребро тетраэдра
вершина тетраэдра
A
C
B
Тетраэдр имеет 4 грани,
6 рёбер и 4 вершины
10.
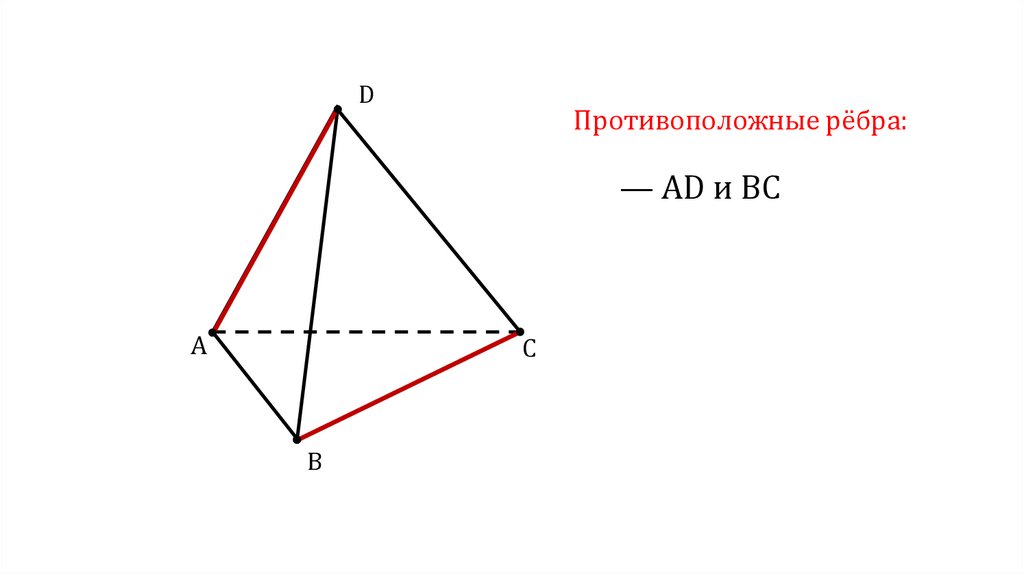
DПротивоположные рёбра:
— AD и BC
A
C
B
11.
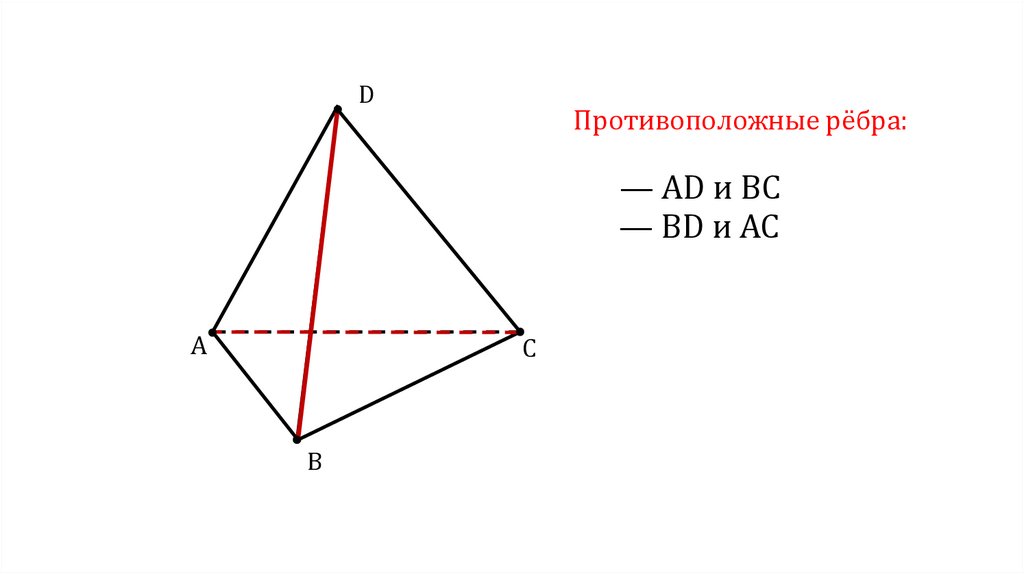
DПротивоположные рёбра:
— AD и BC
— BD и AC
A
C
B
12.
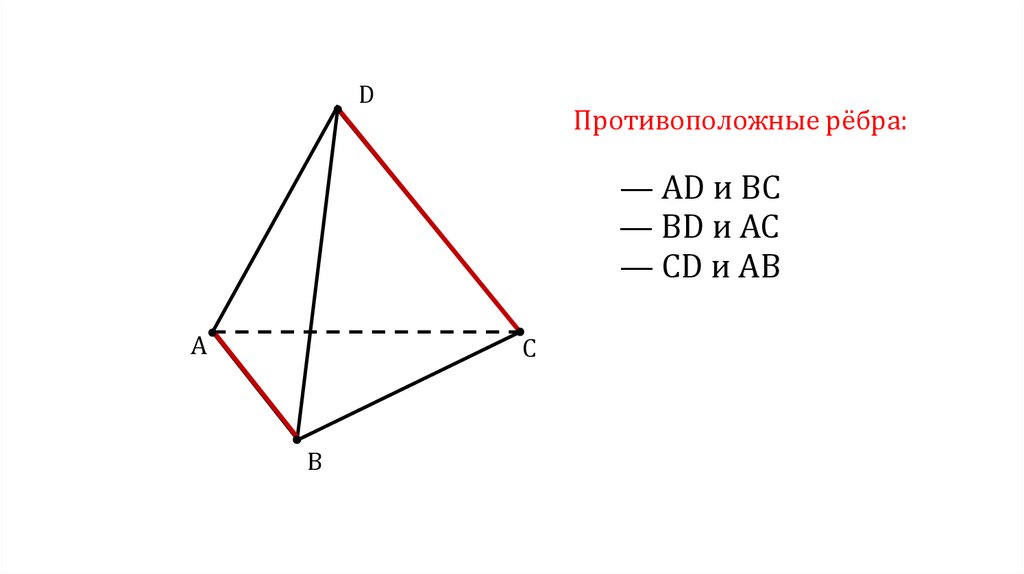
DПротивоположные рёбра:
— AD и BC
— BD и AC
— CD и AB
A
C
B
13.
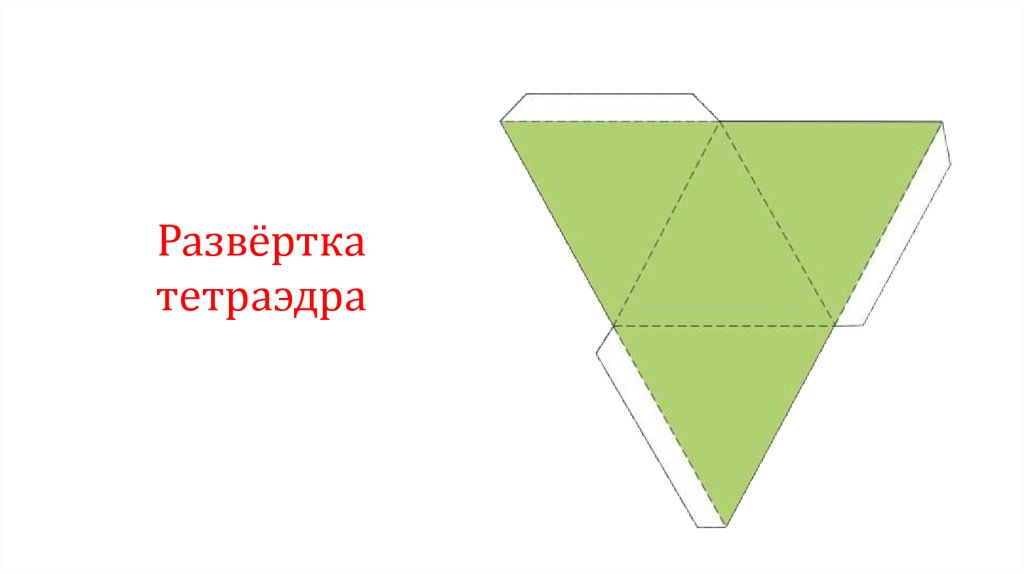
Развёрткатетраэдра
14.
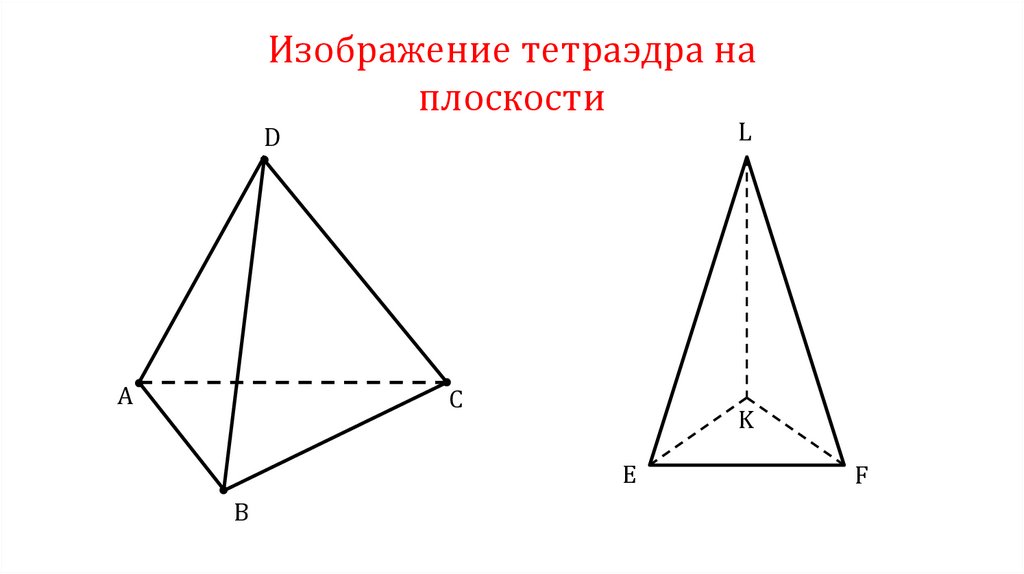
Изображение тетраэдра наплоскости
L
D
A
C
K
E
B
F
15.
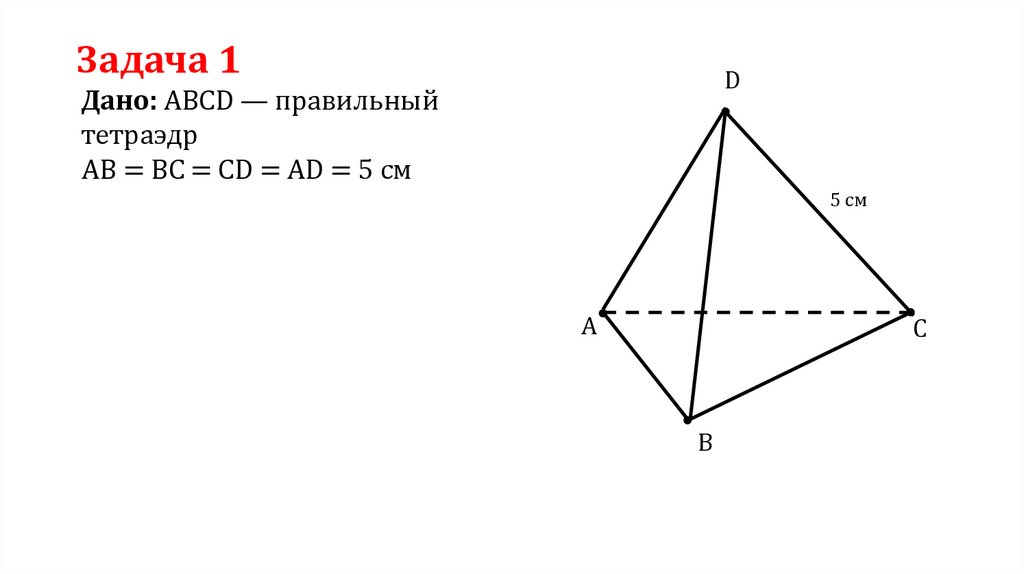
Задача 1D
Дано: ABCD — правильный
тетраэдр
AB = BC = CD = AD = 5 см
5 см
A
C
B
16.
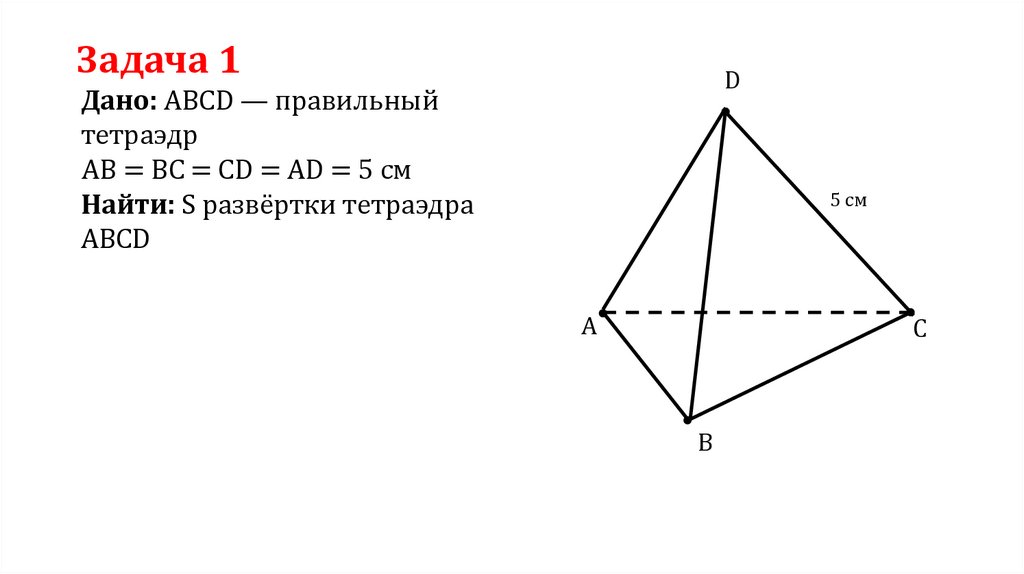
Задача 1D
Дано: ABCD — правильный
тетраэдр
AB = BC = CD = AD = 5 см
Найти: S развёртки тетраэдра
ABCD
5 см
A
C
B
17.
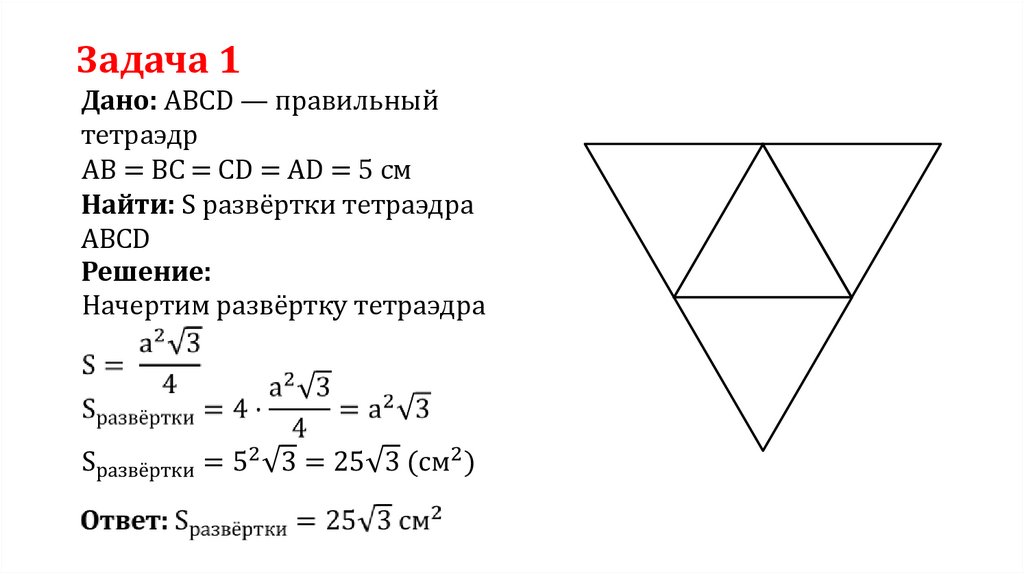
Задача 1Дано: ABCD — правильный
тетраэдр
AB = BC = CD = AD = 5 см
Найти: S развёртки тетраэдра
ABCD
Решение:
Начертим развёртку тетраэдра
18.
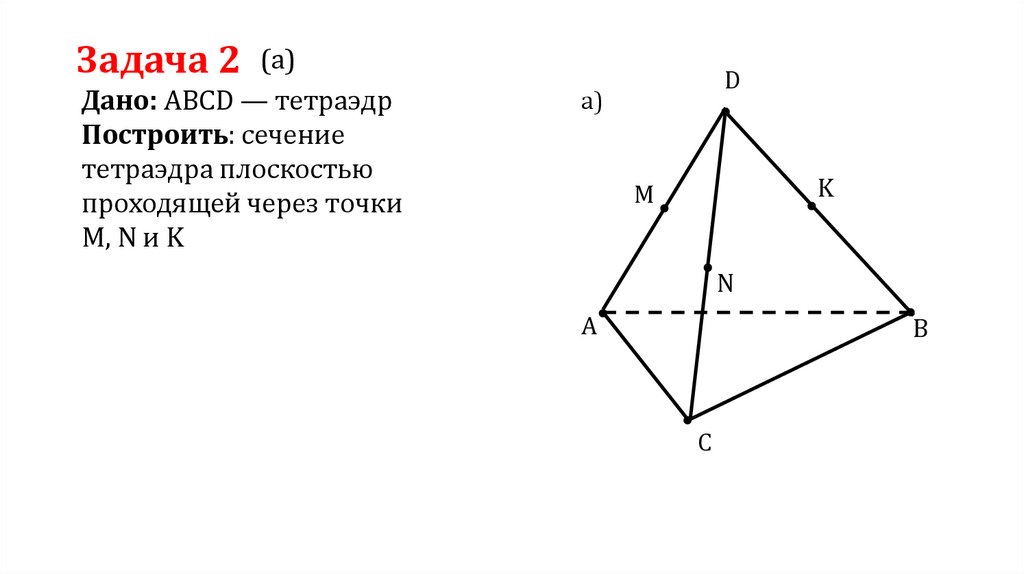
Задача 2(а)
Дано: ABCD — тетраэдр
Построить: сечение
тетраэдра плоскостью
проходящей через точки
M, N и K
D
а)
K
M
N
A
B
C
19.
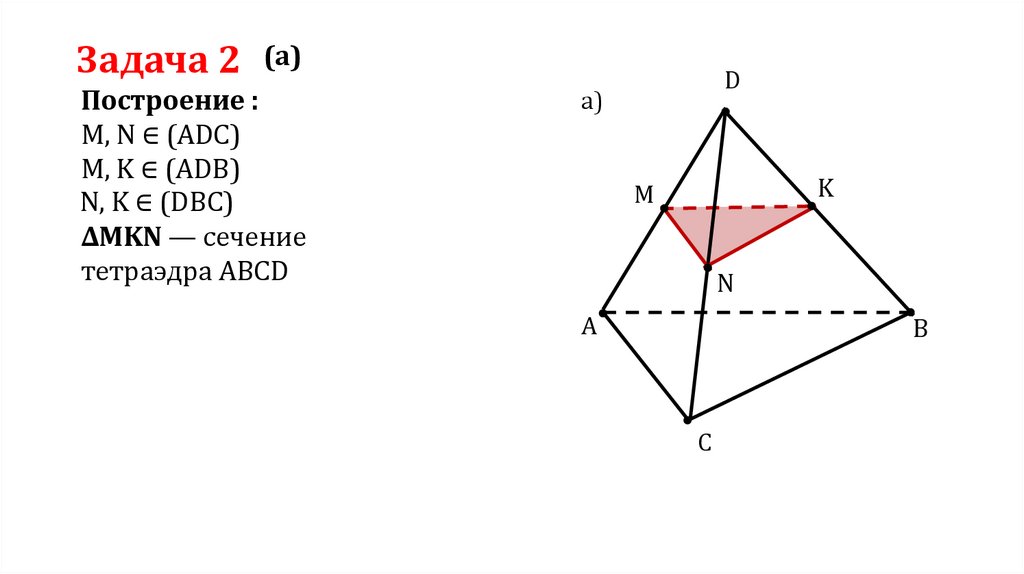
Задача 2(а)
Построение :
M, N ∈ (ADC)
M, K ∈ (ADB)
N, K ∈ (DBC)
∆MKN — сечение
тетраэдра ABCD
D
а)
K
M
N
A
B
C
20.
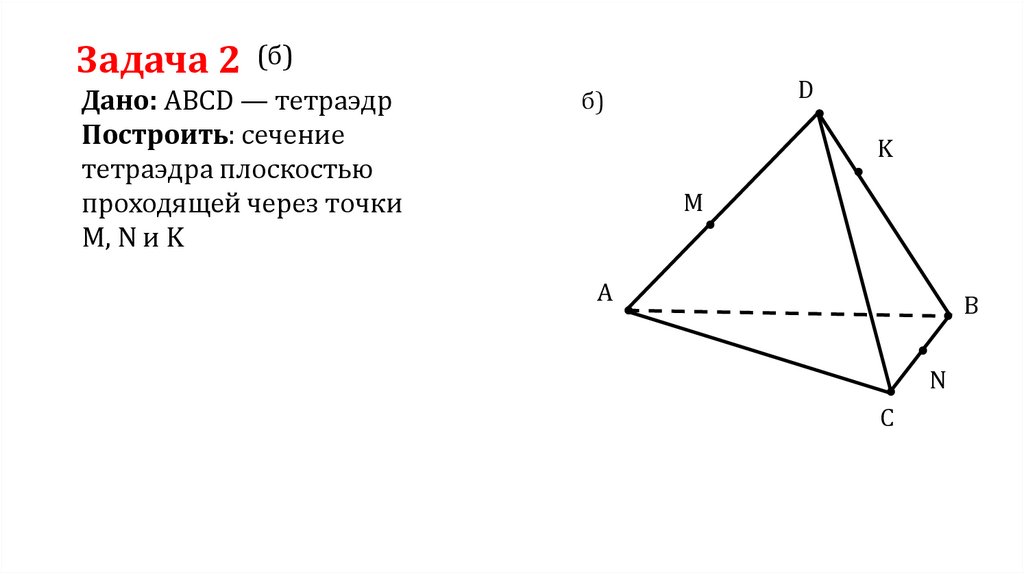
Задача 2(б)
Дано: ABCD — тетраэдр
Построить: сечение
тетраэдра плоскостью
проходящей через точки
M, N и K
D
б)
K
M
A
B
N
C
21.
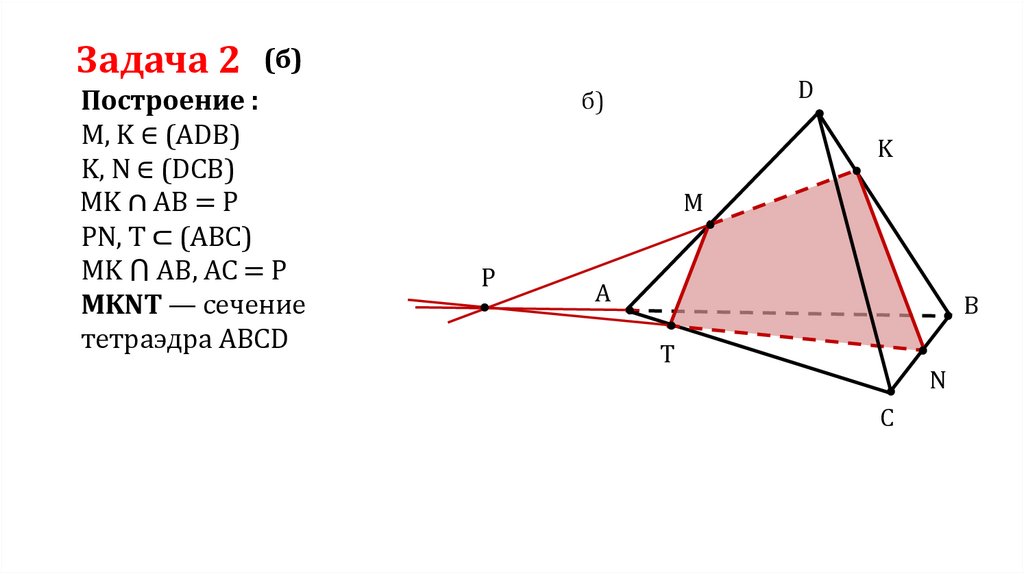
Задача 2(б)
Построение :
M, K ∈ (ADB)
K, N ∈ (DCB)
MK ∩ AB = P
PN, T ⊂ (ABC)
MK ⋂ AB, AC = P
MKNT — сечение
тетраэдра ABCD
D
б)
K
M
P
A
B
T
N
C






 Математика
Математика