Похожие презентации:
Логарифмические уравнения. Способы решения логарифмических уравнений
1.
Тема: «Логарифмическиеуравнения. Способы решения
логарифмических уравнений»
2.
Тема: «Логарифмические уравнения. Способырешения логарифмических уравнений»
• Цель урока: формирование умения решать логарифмические
уравнения разных типов на основе применения определения
логарифма, свойств логарифмов и общих методов решения
уравнений.
Задачи:
а) общенаучная: выбирать рациональные способы решения
уравнений, применять полученные теоретические знания для
решения уравнений;
• б) воспитательная: воспитывать сознательное отношение к
учению, познавательную активность и интерес к предмету,
культуру умственного труда;
в) развивающая: развивать навыки сравнительного анализа,
логического мышления, умение делать обобщения и выводы;
• Тип урока: комбинированный
3.
Оборудование и материалы:1. Тест для первичного закрепления.
2. Раздаточный материал.
3. Оценочный лист.
4. Компьютер.
5. Презентация.
Методы обучения: наглядный, проблемный
Формы организации урока: индивидуальная,
фронтальная, групповая.
Технологии, используемые на уроке: групповая
технология, обучение в сотрудничестве, информационнокоммуникативная.
4.
5.
6.
7.
8.
Способы решения простейшихлогарифмических уравнений
1.
2.
Решение уравнений на основании
определения логарифма, например,
уравнение loga х = б (а > 0, а≠ 1, б>0 ) имеет решение
х = аb.
Метод потенцирования. Под потенцированием
понимается переход от равенства,
содержащего логарифмы, к равенству, не
содержащему их:
если , loga f(х) = loga g(х), то f(х) = g(х), f(х)>0, g(х)>0 , а
> 0, а≠ 1.
9.
Уравнение, содержащее неизвестное под знаком логарифма или (и) вего основании, называется логарифмическим уравнением.
log a f ( x) b
log f ( x ) b a
1. Решение логарифмических уравнений на основании определения
логарифма.
Определение логарифма:
log a b c : a c b, a 0, b 0, a 1.
log a f ( x ) c f ( x ) a c ,
Пример 1:
f ( x ) 0, a 0, a 1.
log 4 x 2,
ОДЗ : х 0,
x 42 ,
x 16.
Ответ: 16.
10.
11.
Ответ: х=212.
13.
2. Метод потенцирования.Под потенцированием понимается переход от равенства, содержащего
логарифмы, к равенству, не содержащему их.
log a f ( x ) log a g ( x ) f ( x ) g ( x ), где a 0, a 1, f ( x ) 0, g ( x ) 0.
Пример :
log 2 ( x 2 7 x 5) log 2 (4 x 1),
x 2 7 x 5 4 x 1,
x 2 3x 4 0,
x1 1, x2 4.
Проверка:
x 1 log 2 (12 7 1 5) log 2 (4 1 1) log 2 3 log 2 3 - верно
2
x 4 log 2 (( 4) 7 ( 4) 5) log 2 (4 ( 4) 1) log 2 ( 17) log 2 ( 17)
- не верно
Ответ: 1.
В таких уравнениях обязательна проверка или нахождение ОДЗ.
14.
15.
Решите логарифмическиеуравнения:









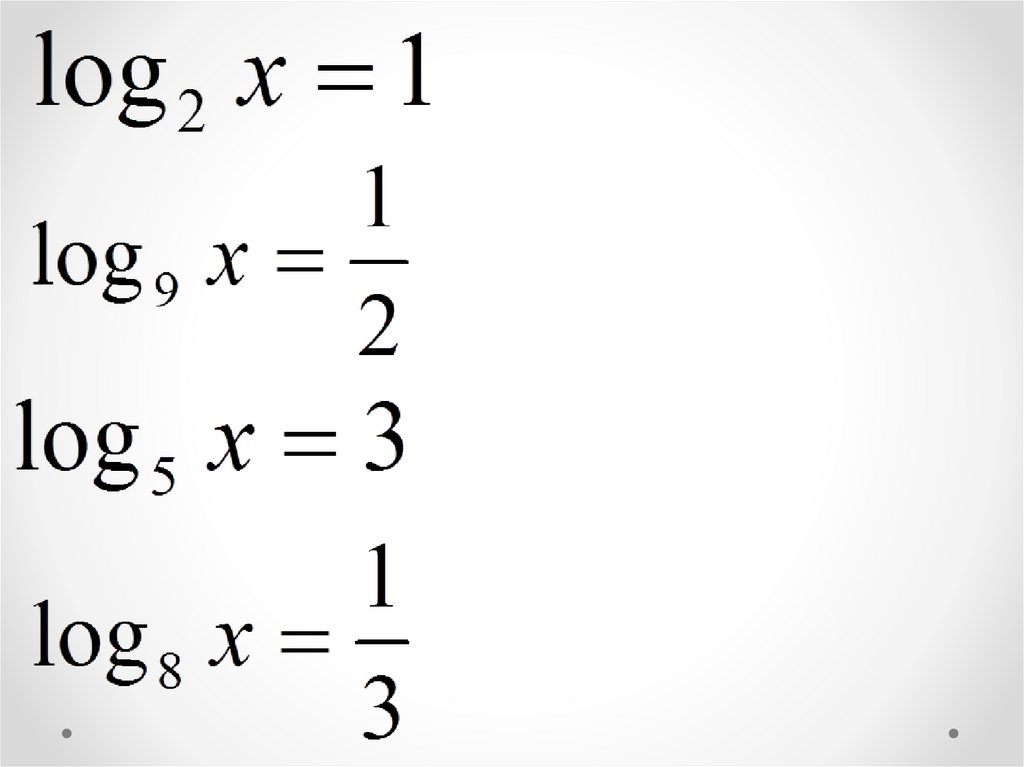






 Математика
Математика








