Похожие презентации:
Квадратичная функция и её график
1. Квадратичная функция и её график.
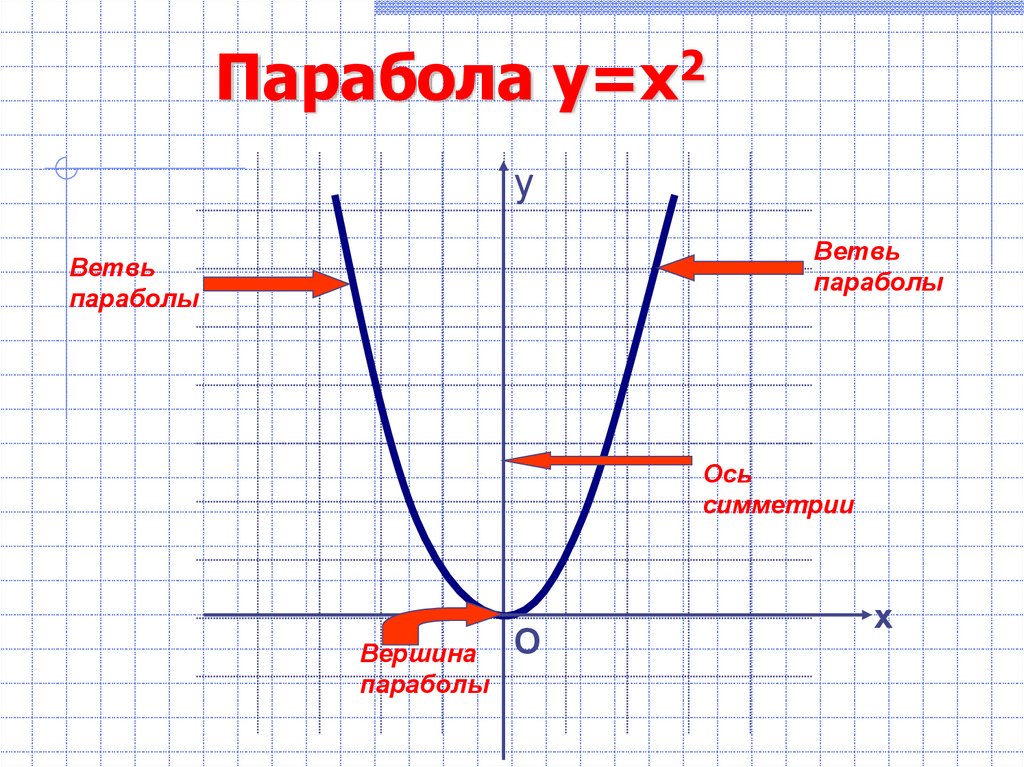
2. Парабола y=х2
уВетвь
параболы
Ветвь
параболы
Ось
симметрии
Вершина
параболы
О
х
3.
2x
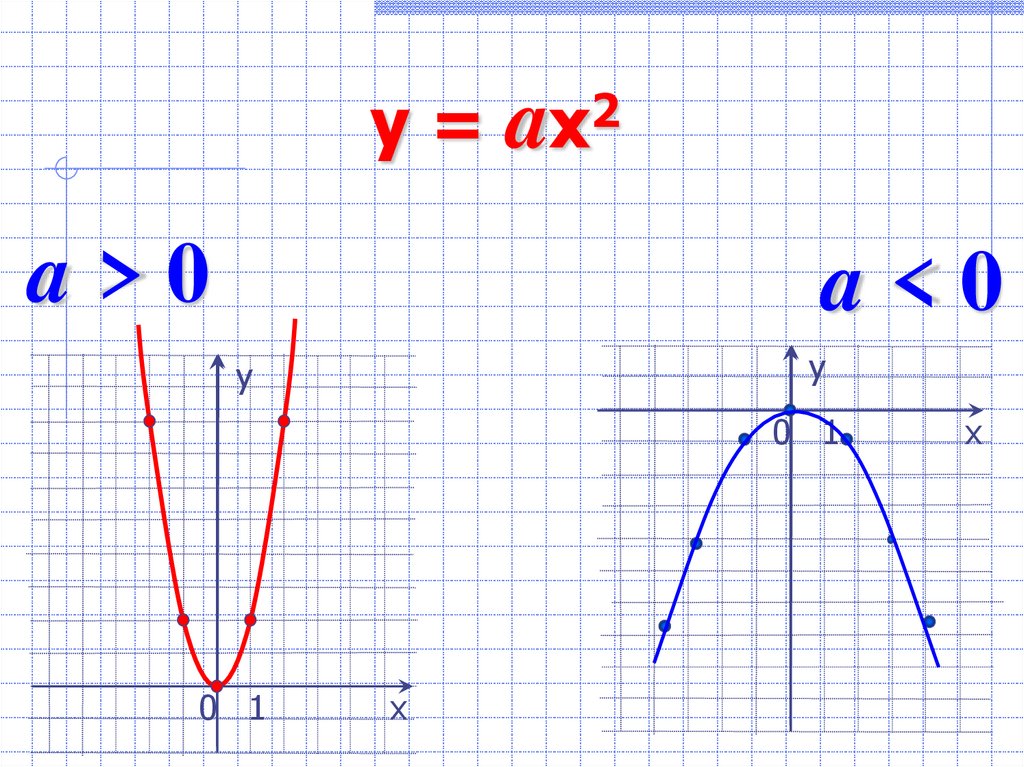
y=a
a>0
a<0
у
у
0 1
0 1
х
х
4.
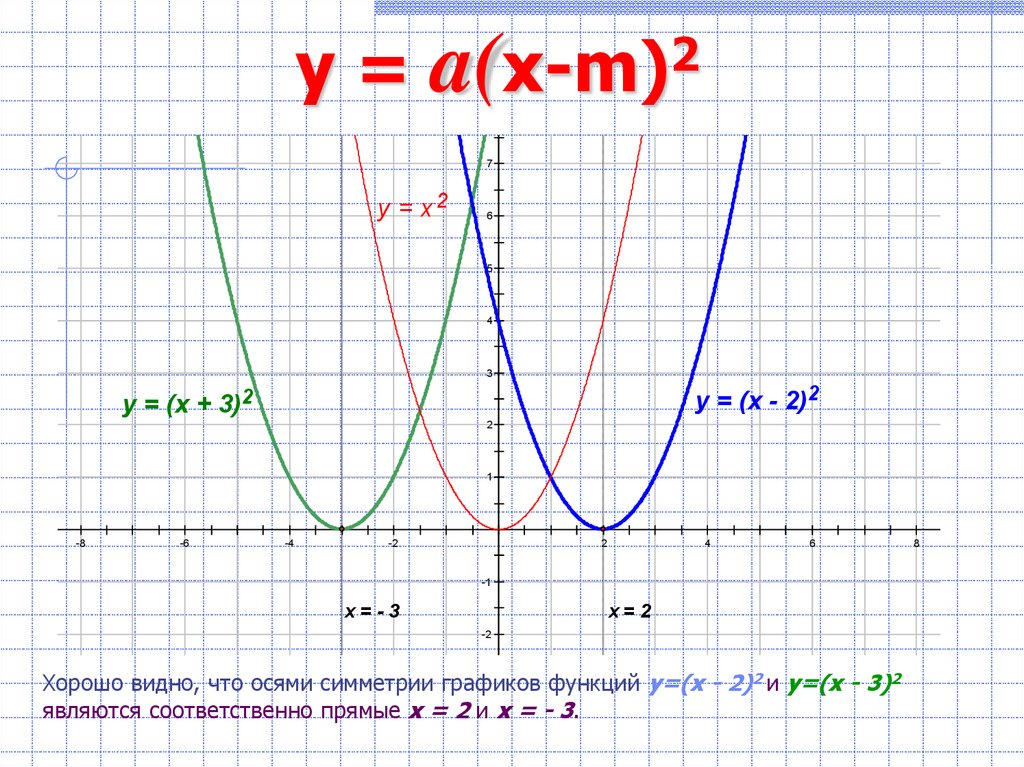
y = a(2
x-m)
8
7
у = х2
6
5
4
3
у = (х - 2)2
у = (х + 3)2
2
1
-8
-6
-4
-2
2
4
6
-1
х= -3
х= 2
-2
-3
Хорошо видно, что осями симметрии графиков
функций y=(x - 2)2 и y=(x - 3)2
являются соответственно прямые х = 2 и х = - 3.
-4
8
5.
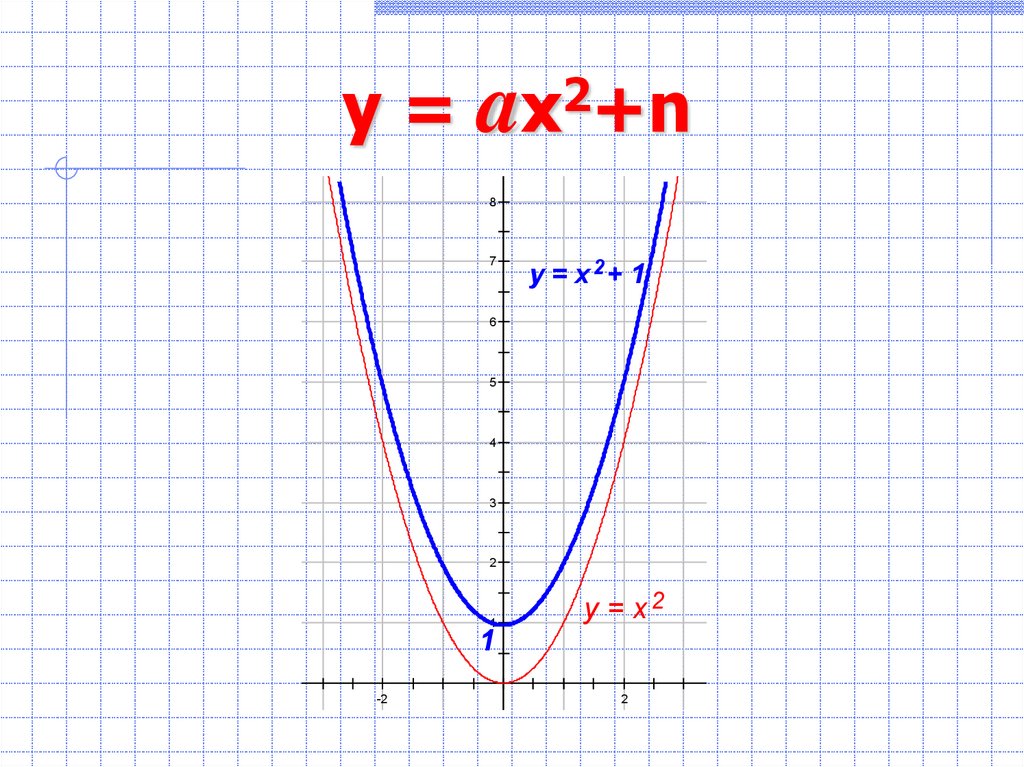
2x +n
y=a
8
7
у = х 2+ 1
6
5
4
3
2
1
у = х2
1
-8
-6
-4
-2
2
-1
4
6
8
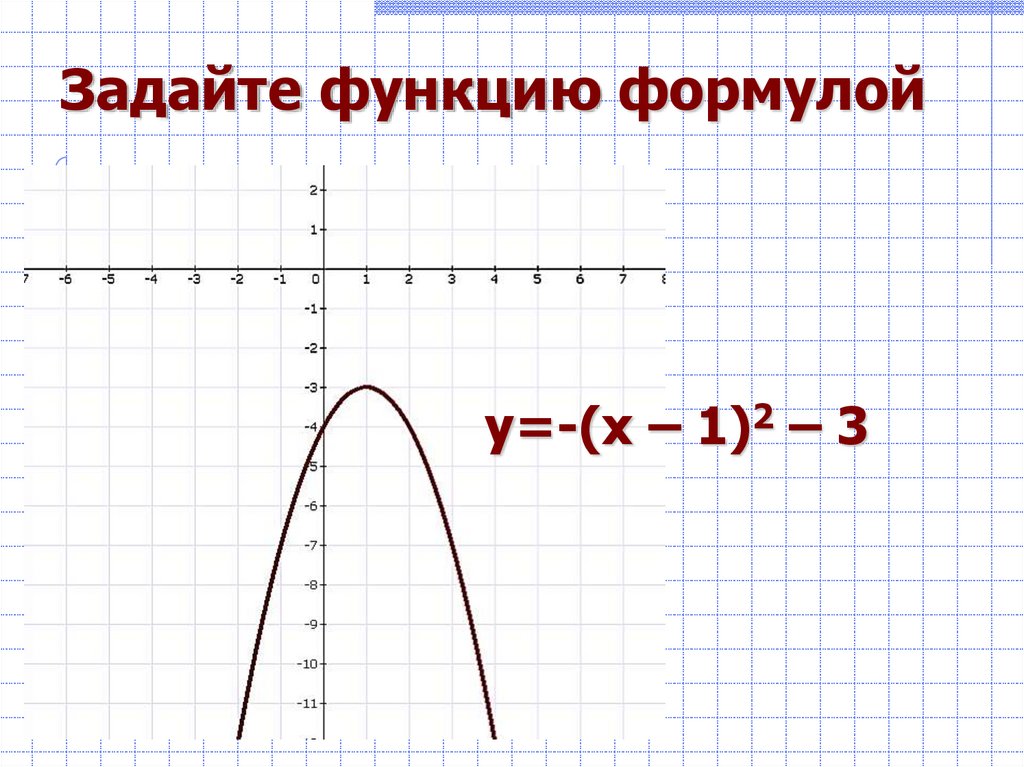
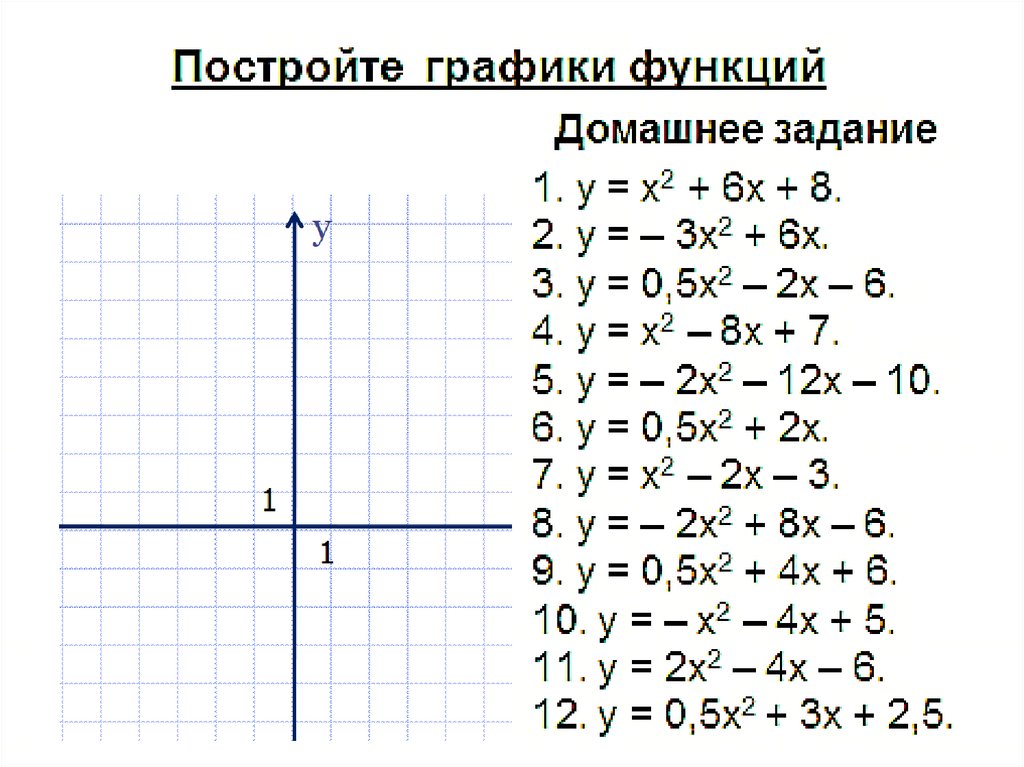
6. Задайте функцию формулой
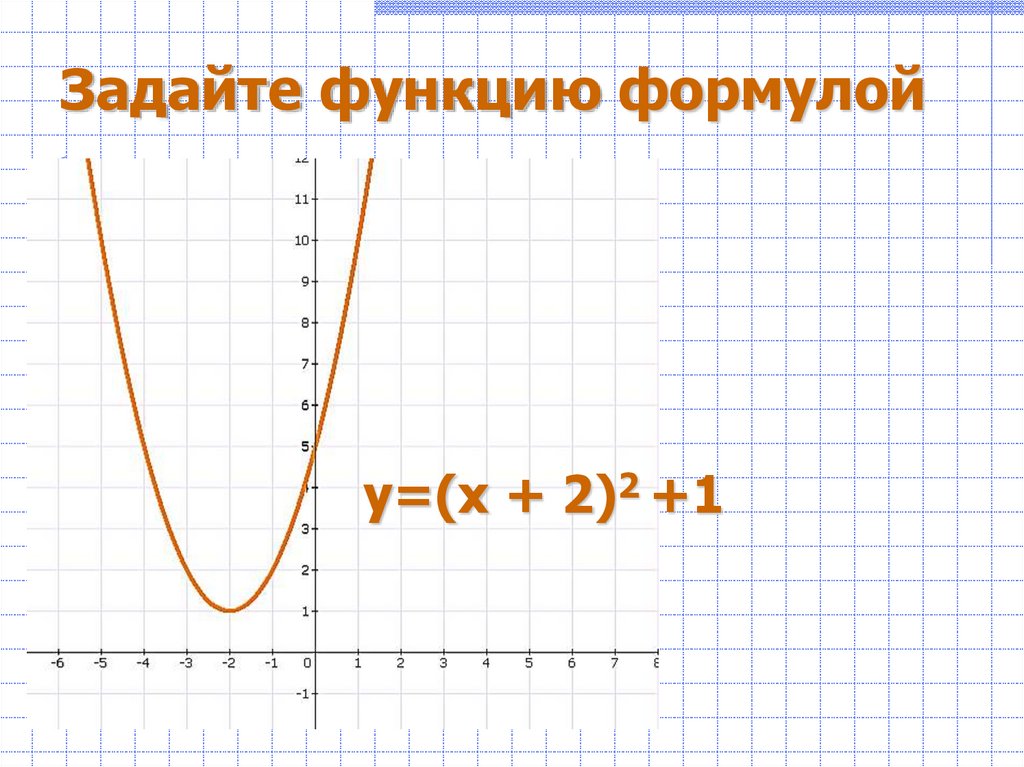
у=-(х – 1)2 – 37. Задайте функцию формулой
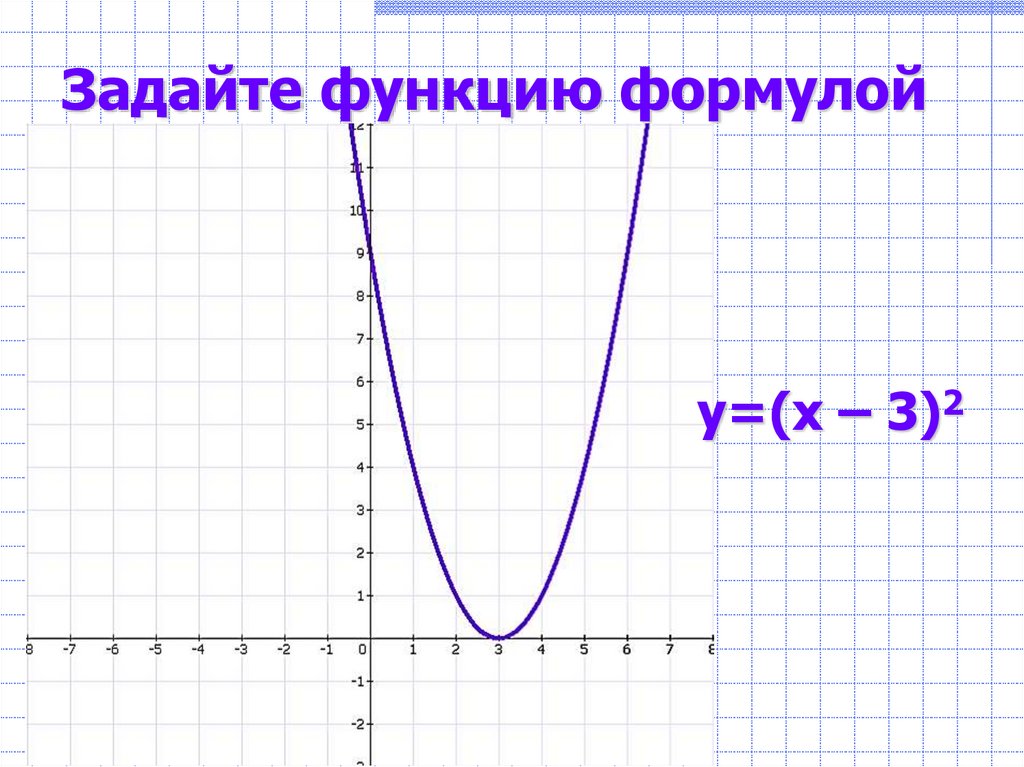
у=(х + 2)2 +18. Задайте функцию формулой
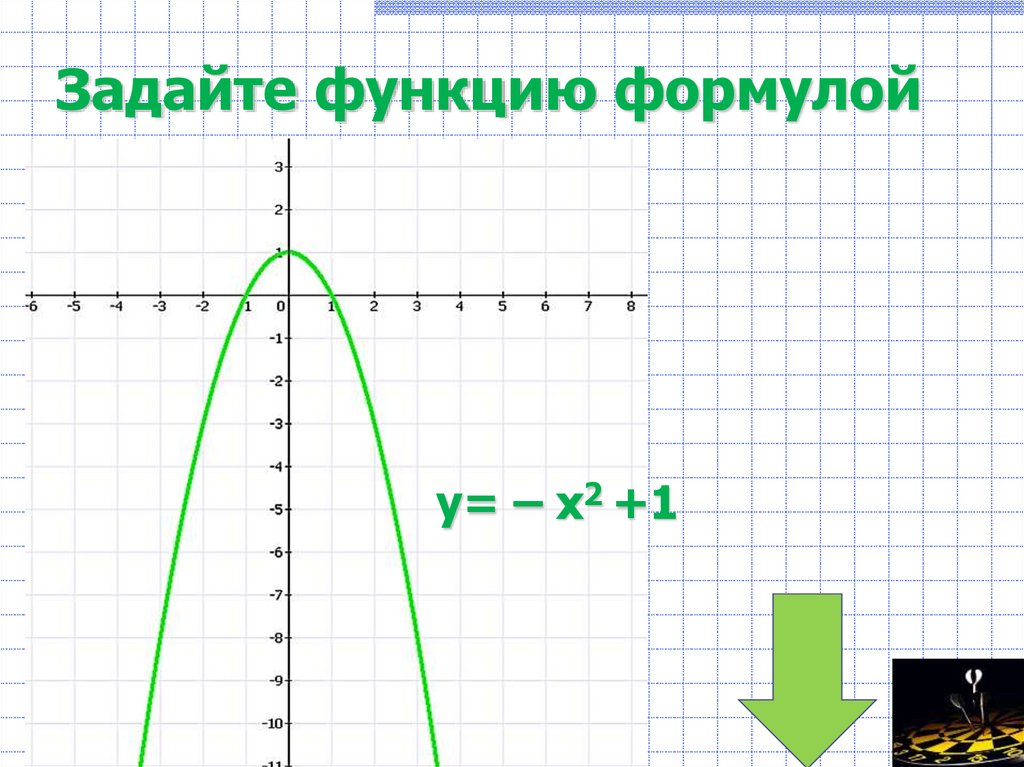
у=(х – 3)29. Задайте функцию формулой
у= – х2 +110.
Определение квадратичнойфункции
Квадратичной функцией
называется функция , которая задается
формулой вида:
y=
2
ax +bx
+c
где: a,b,c –
числа
х – независимая переменная
а 0
11.
Мы уже строили графики функций видау = ах2 + bх + с , выделяя квадрат двучлена.
Используем этот прием в общем виде:
ах2
+ bx + с
=
2
b
b2
= а x 2
x 2
2a
4a
а
(х2
b
+
x)+с =
a
b2
2 + с =
4a
2
2
2
2
b
4
ac
b
b
b
= а x
+ с = а x
2
2a
4a
2a
4a
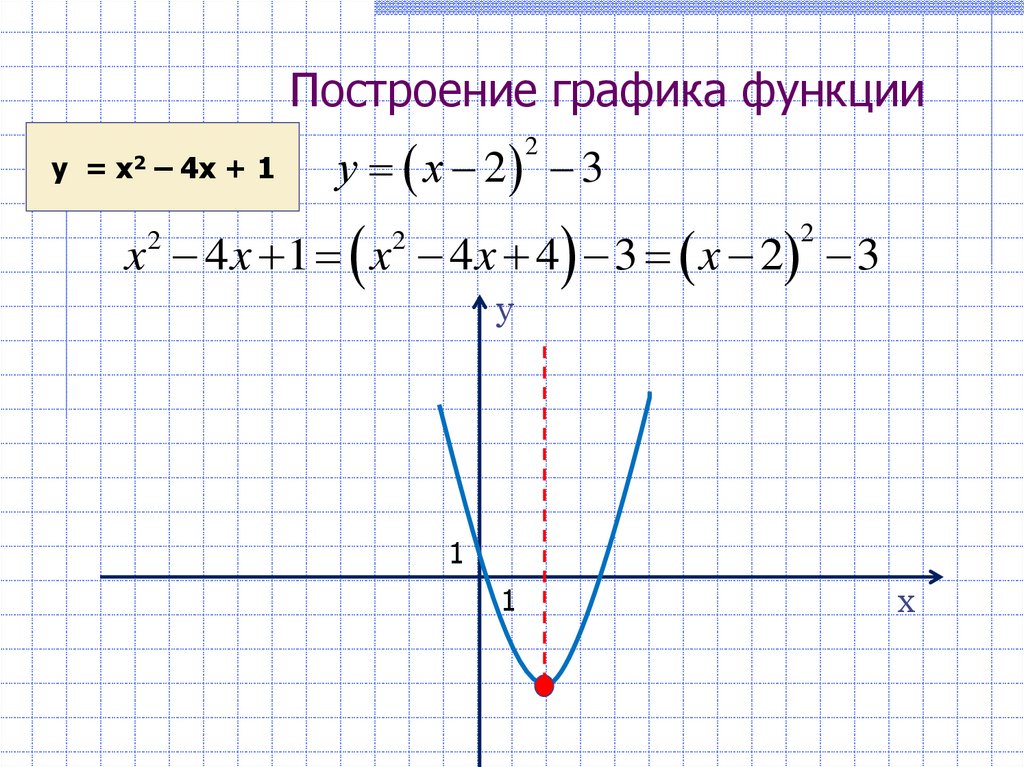
12. Построение графика функции
у =х2
– 4х + 1
у x 2 3
2
x 4 x 1 x 4 x 4 3 x 2 3
2
2
2
у
1
1
х
13.
Нам удалось преобразовать квадратный трехчлен кприведенному виду у = а ( х – x0)2 + y0,
Теперь если
b
x 0 , y 0 у х0
2a
, то получаем ,
чтобы построить график функции у = ах2 + bx + с,
надо выполнить параллельный перенос параболы
у = ах2, чтобы вершина оказалась в точке ( x0 ; y0 )
14.
-Таким образом, мы доказали теорему:
.
Графиком квадратичной функции
у = ах2 + bх + с является парабола,
которая получается из параболы
у = ах2 параллельным переносом.
Вершина параболы -
b
где : хо =
2a
( х0; уо) ,
у0 = у х0
b
Осью параболы будет прямая х
2a
15. Алгоритм построения параболы у = ах2 + bх + с :
График любой квадратичной функции –парабола.
Алгоритм построения
параболы у = ах2 + bх + с :
1.Найти координаты вершины параболы,
построить на координатной плоскости
соответствующую точку, провести ось
симметрии.
2.Определить направление ветвей параболы.
3.Найти координаты еще нескольких точек ,
принадлежащих искомому графику ( в
частности, координаты точки пересечения
параболы с осью у).
4.Отметить на координатной плоскости
найденные точки и соединить их плавной
линией.
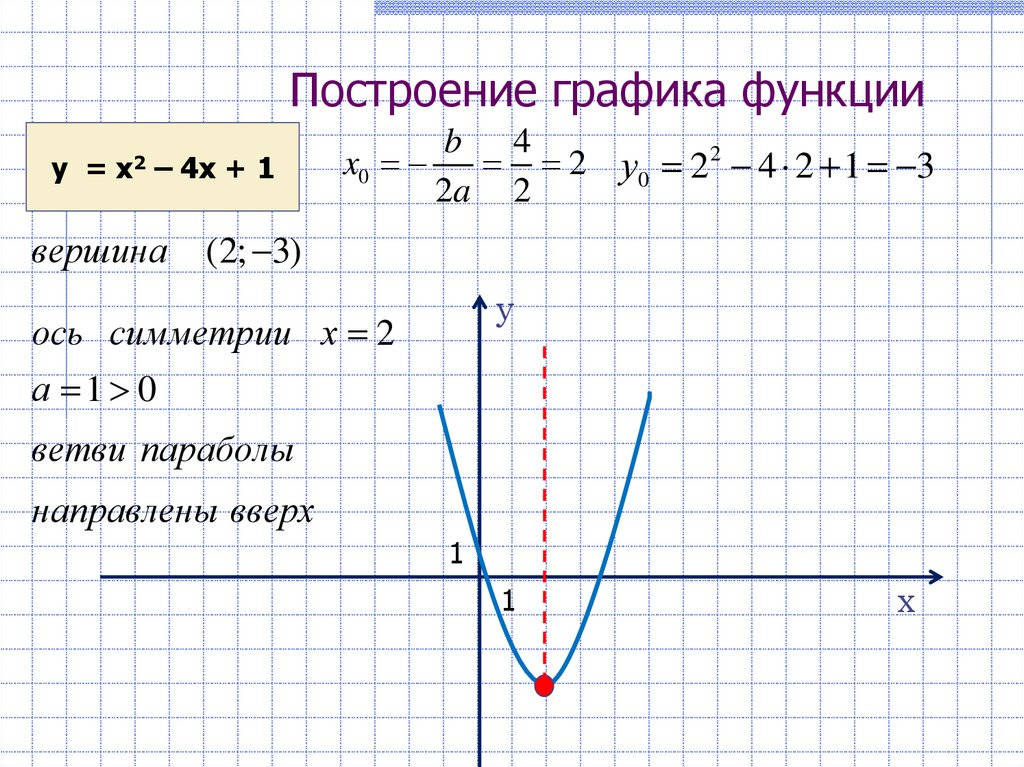
16. Построение графика функции
у = х2 – 4х + 1вершина
b 4
x0
2 у0 22 4 2 1 3
2a 2
(2; 3)
у
ось симметрии х 2
а 1 0
ветви параболы
направлены вверх
1
1
х
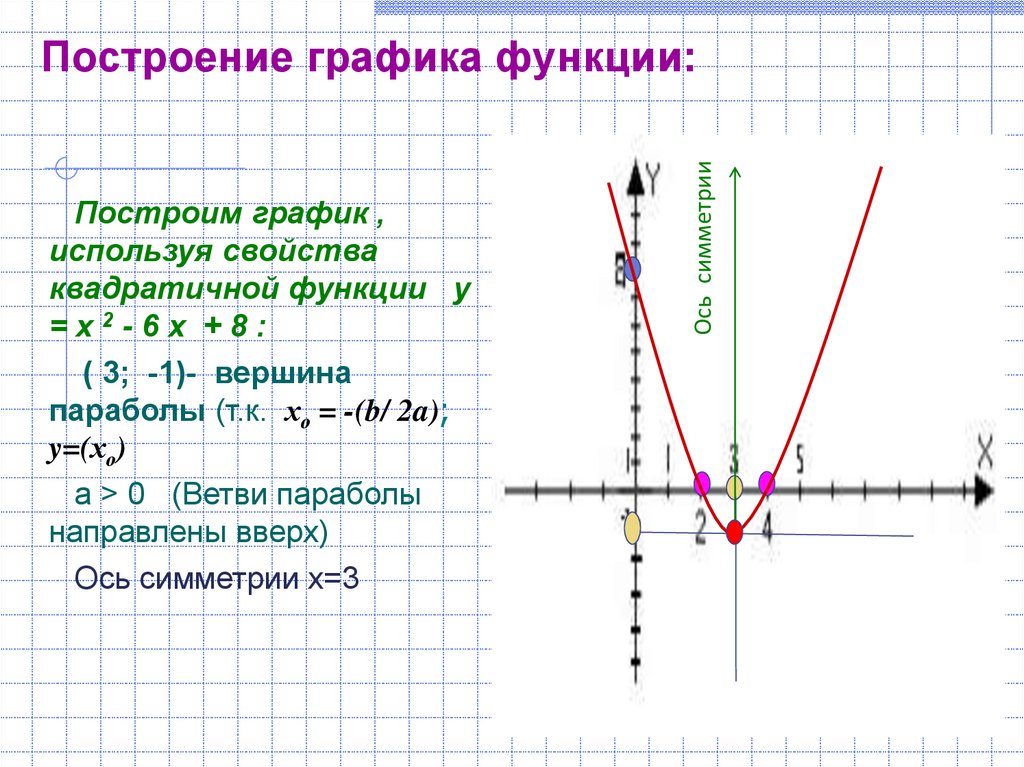
17. Построение графика функции:
Построим график ,используя свойства
квадратичной функции у
=х2-6х +8:
( 3; -1)- вершина
параболы (т.к. хо = -(b/ 2a);
y=(хо)
а > 0 (Ветви параболы
направлены вверх)
Ось симметрии х=3
Ось симметрии
Построение графика функции:








 Математика
Математика








