Пирамида. Правильные многоугольники

1.

2.

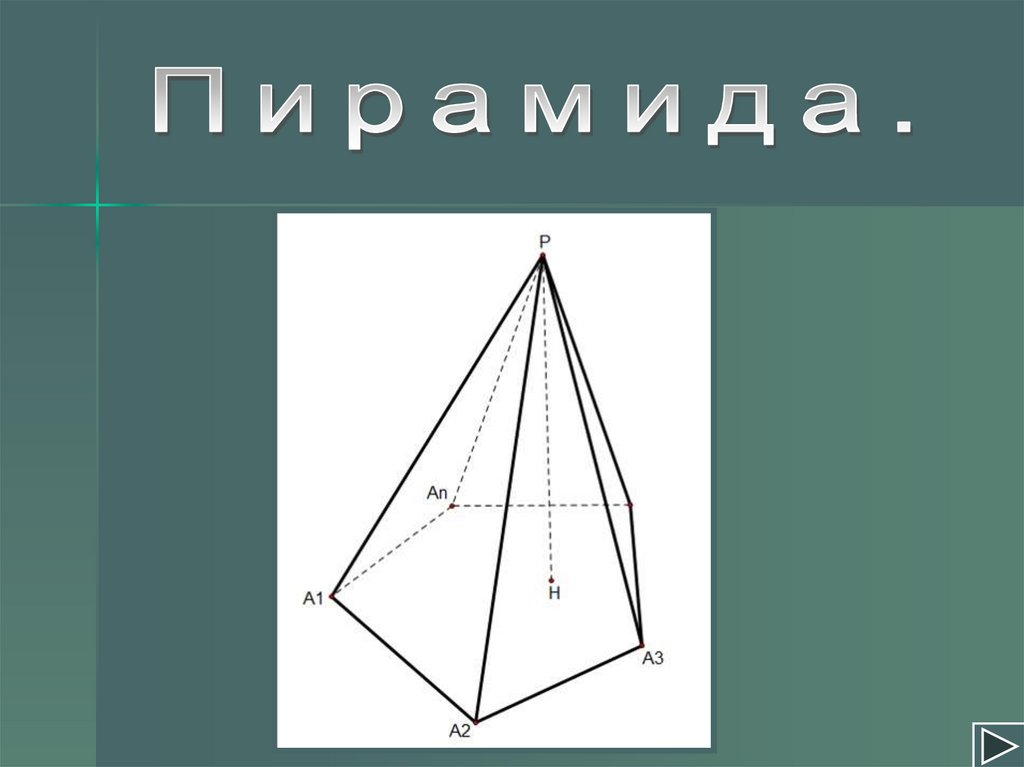
Р
Аn
О
А1
Н
А2
Н1
А3

3.

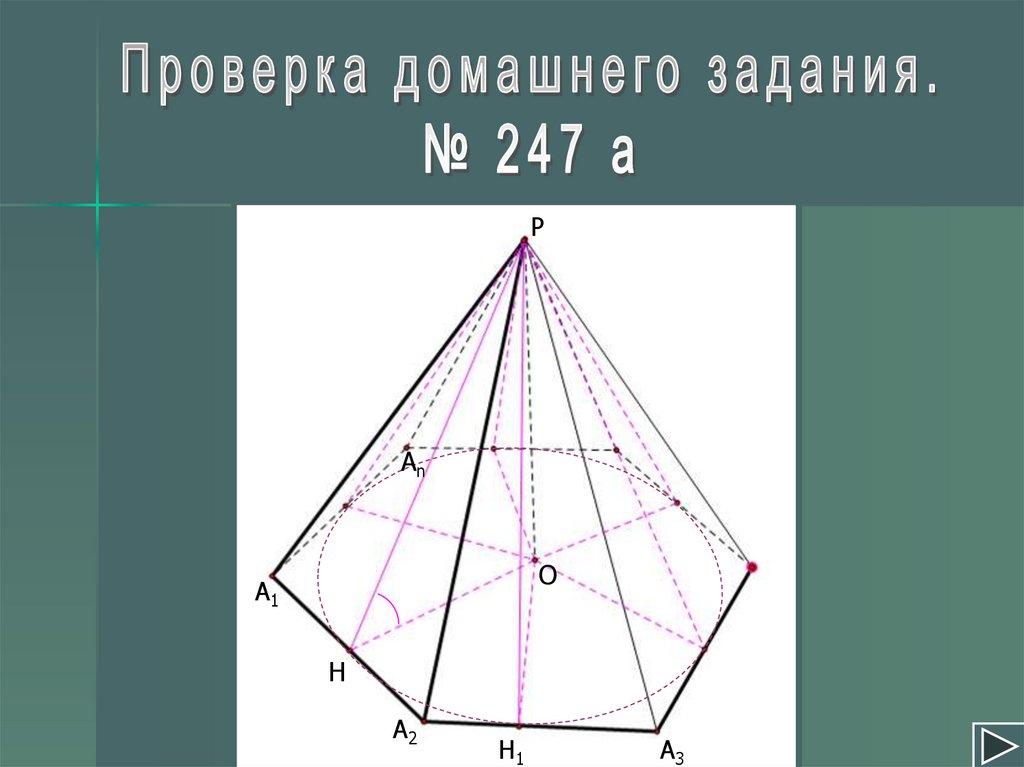
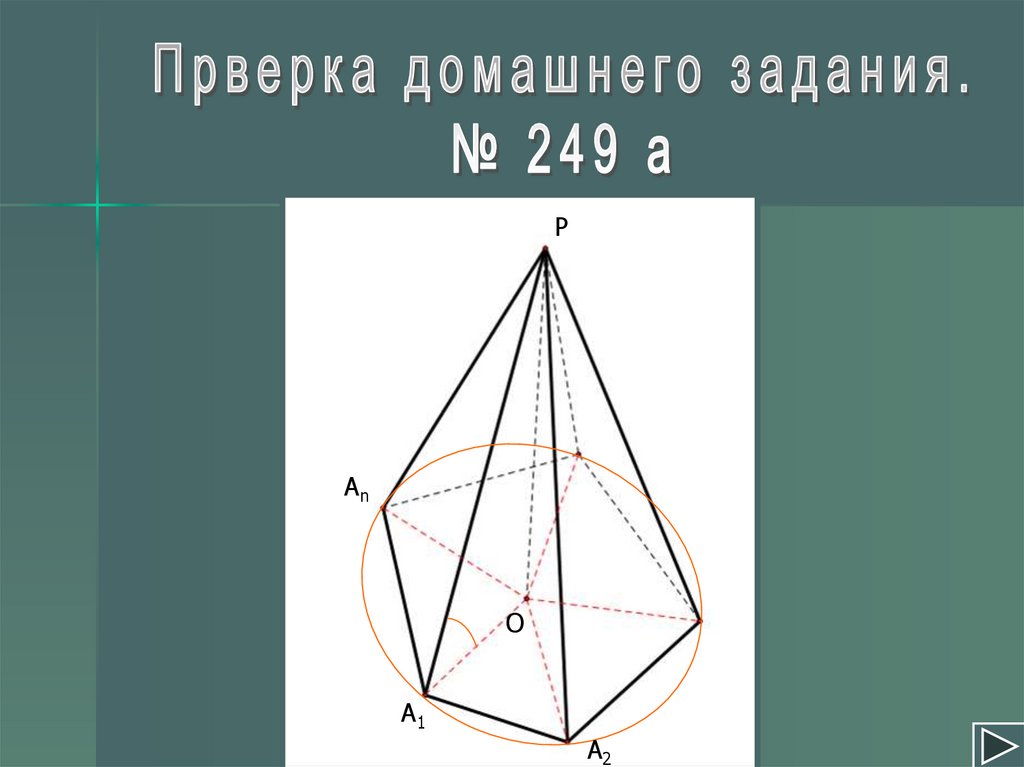
Р
Аn
О
А1
А2

4.

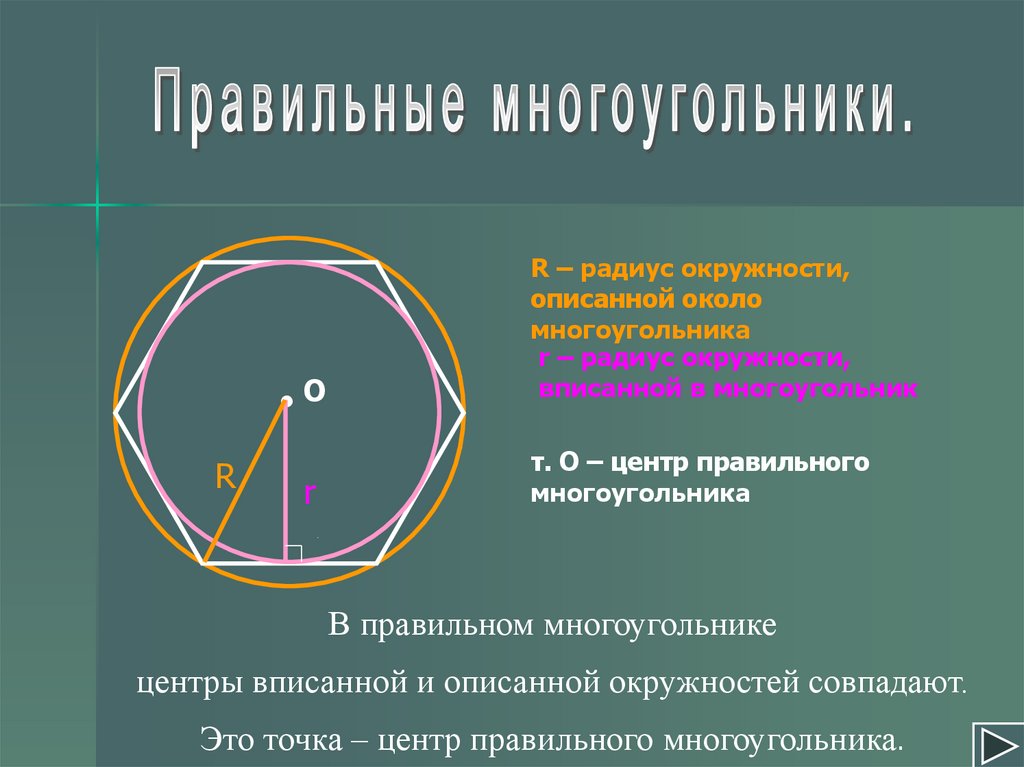
R
О
R – радиус окружности,
описанной около
многоугольника
r – радиус окружности,
вписанной в многоугольник
r
т. О – центр правильного
многоугольника
В правильном многоугольнике
центры вписанной и описанной окружностей совпадают.
Это точка – центр правильного многоугольника.

5.

Формулы для вычисления элементов
правильного многоугольника:
180
an 2 R sin
, r R cos 180 ,
180
n
an 2rtg
.
n
n
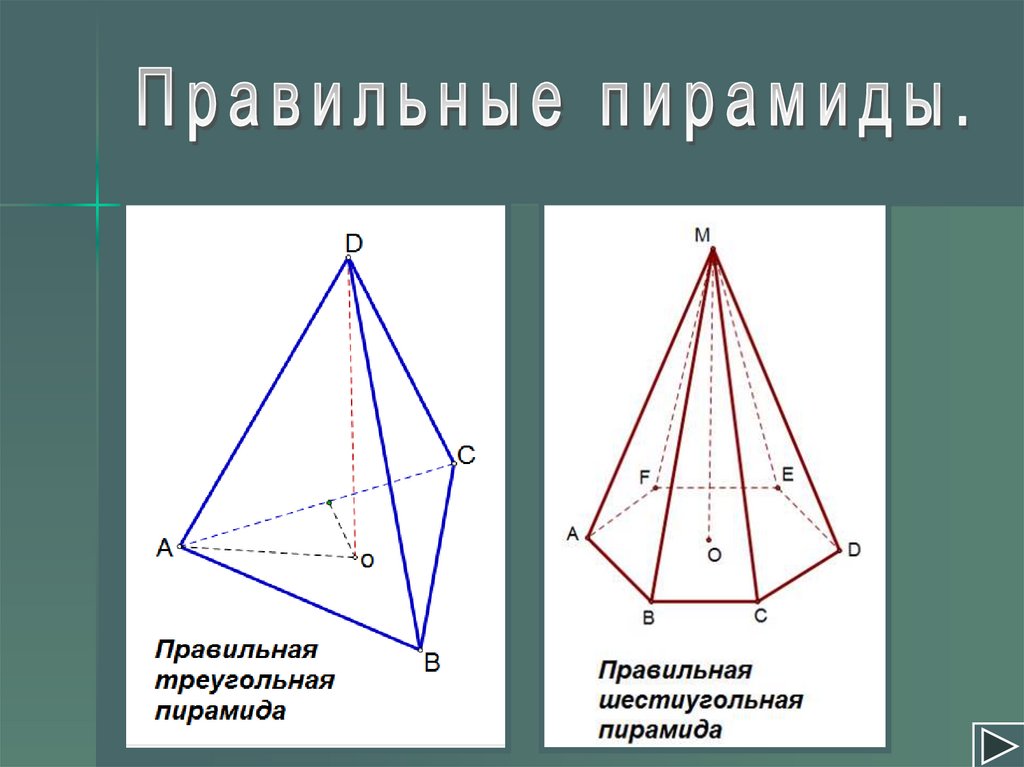
квадрат
равносторонний
треугольник
правильный
шестиугольник
правильный
восьмиугольник

6.

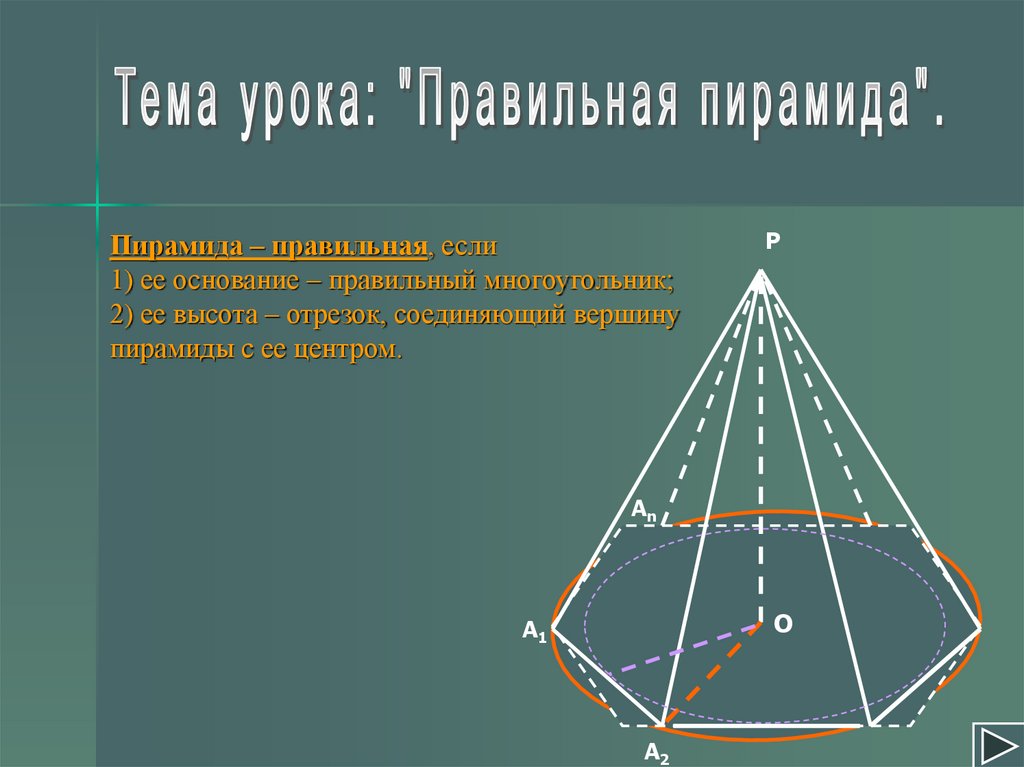
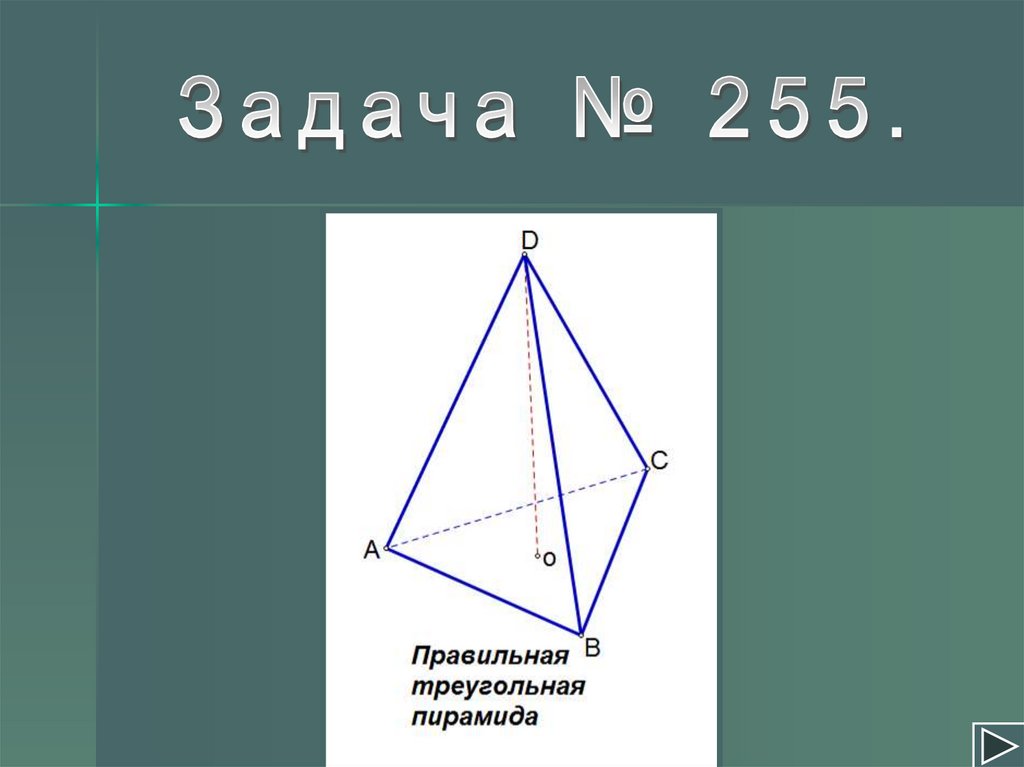
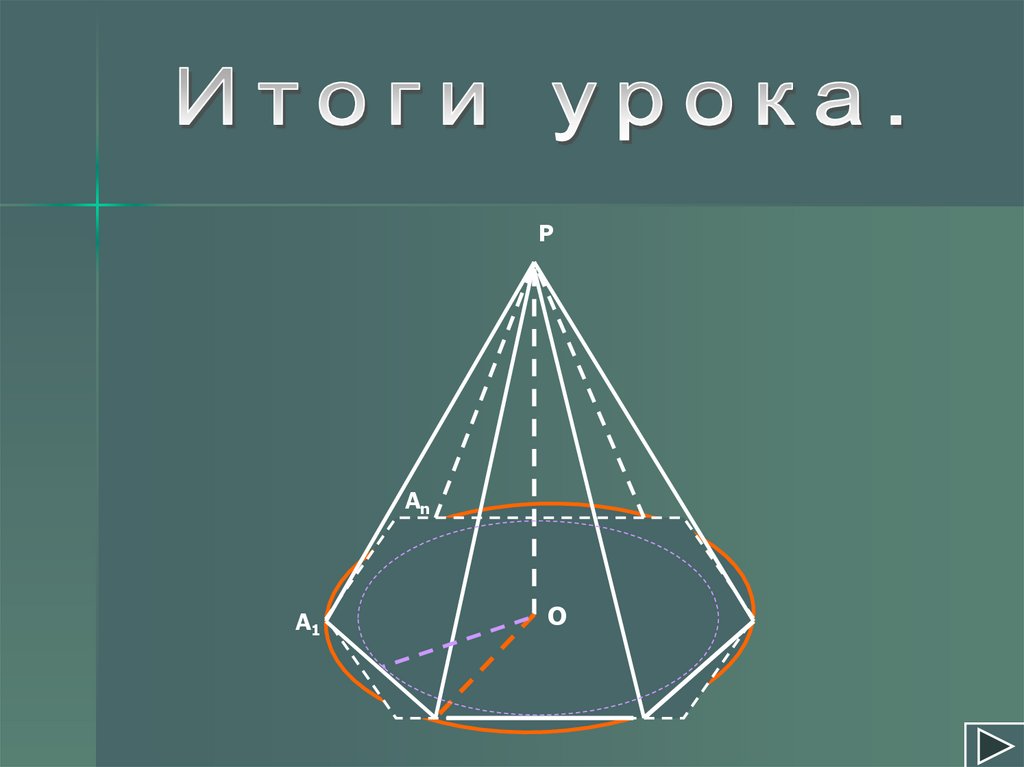
Пирамида – правильная, если
1) ее основание – правильный многоугольник;
2) ее высота – отрезок, соединяющий вершину
пирамиды с ее центром.
Р
Аn
О
А1
А2

7.

8.

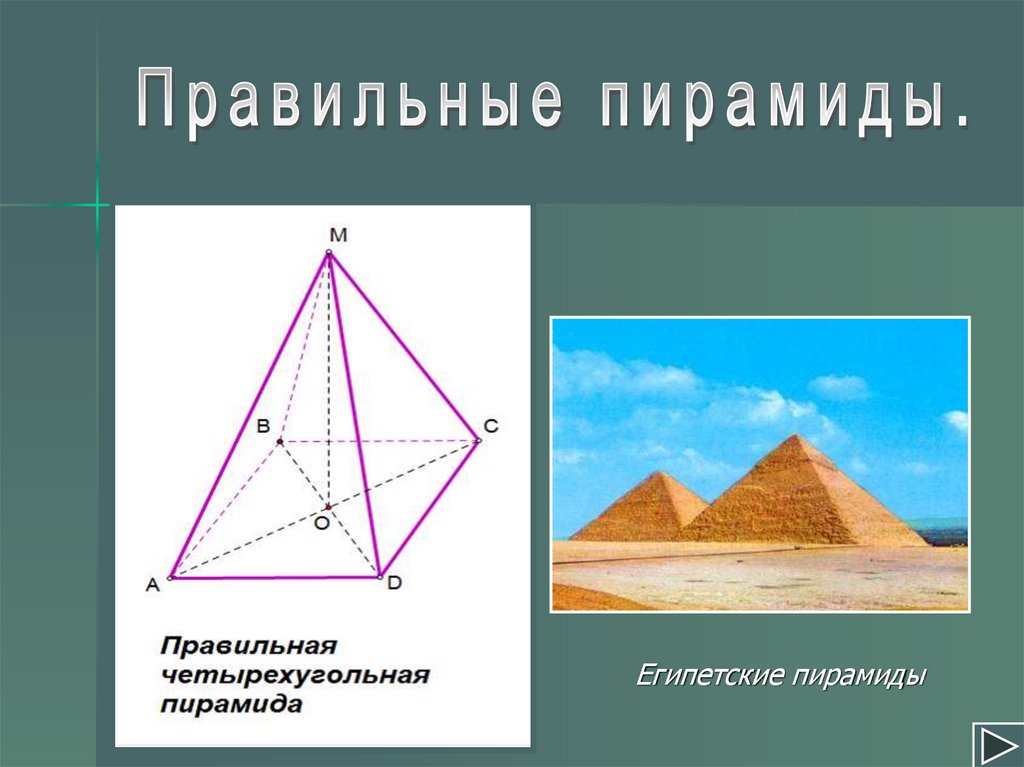
Египетские пирамиды

9.

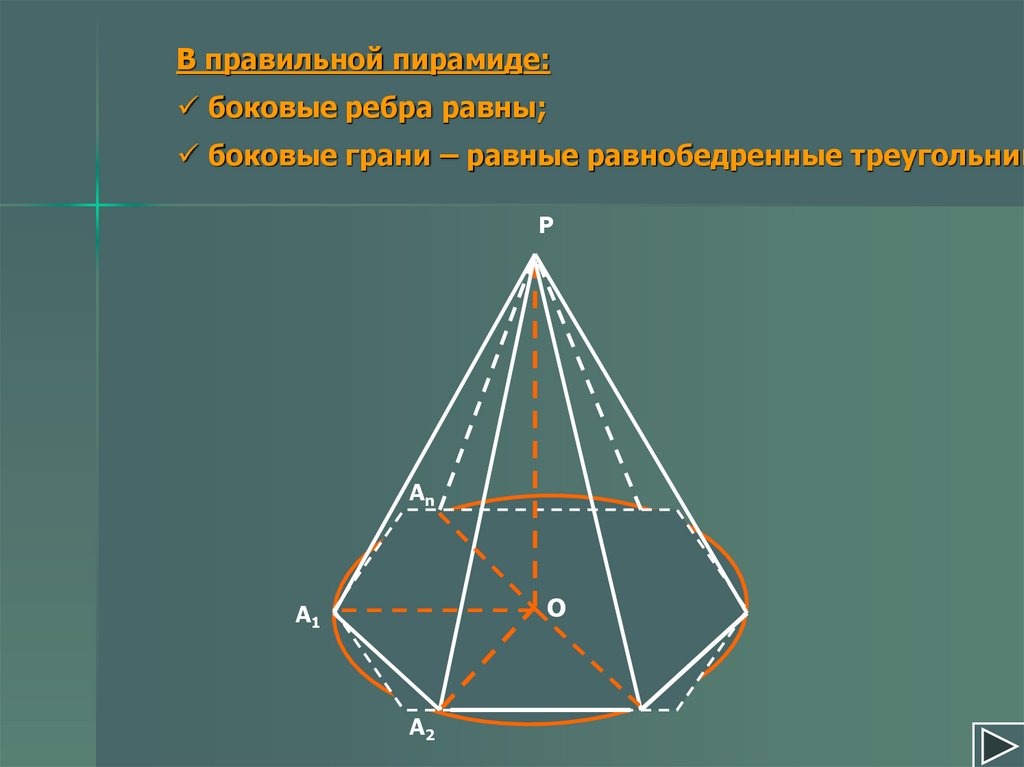
В правильной пирамиде:
боковые ребра равны;
боковые грани – равные равнобедренные треугольник
Р
Аn
О
А1
А2

10.

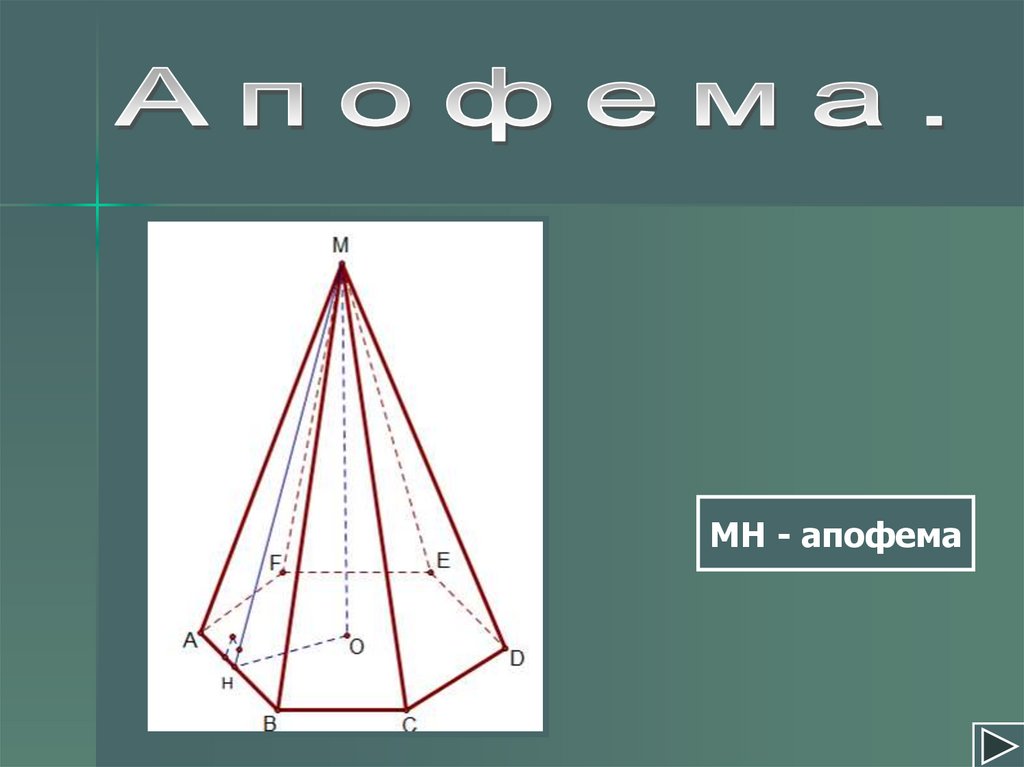
МН - апофема

11.

В правильной четырехугольной
пирамиде построить:
а) угол между боковым ребром и
плоскостью основания;
б) линейный угол двугранного угла при
основании;
в) линейный угол двугранного угла
между боковыми гранями.

12.

13.

Р
Аn
А1
О

14.

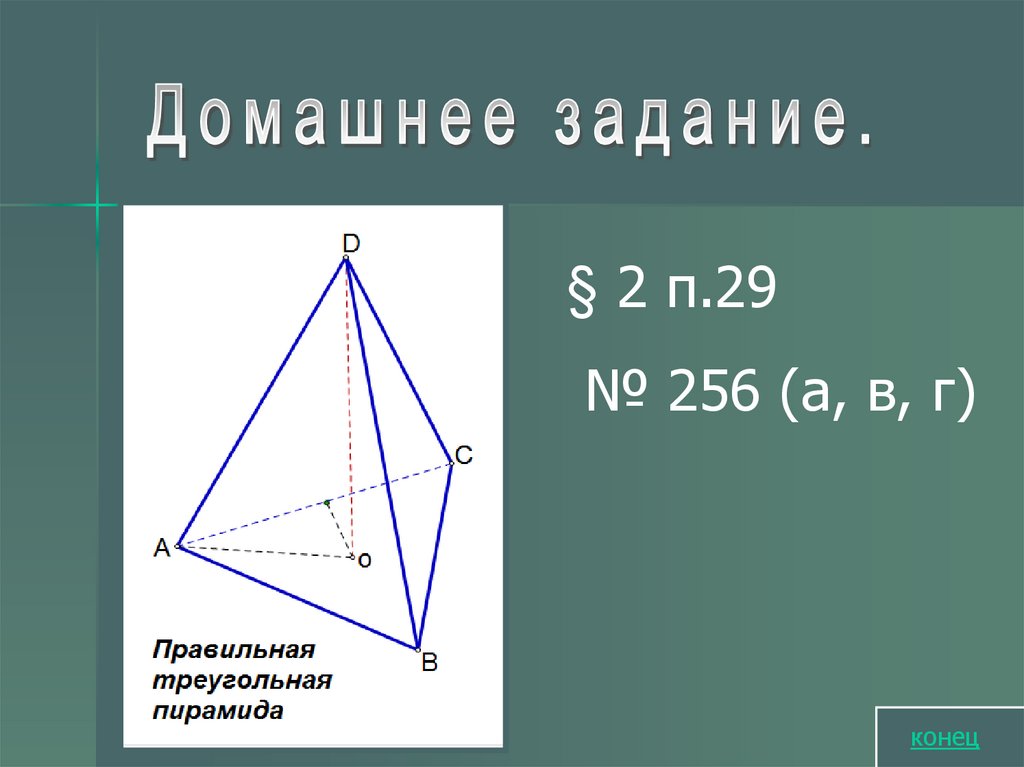
§ 2 п.29
№ 256 (а, в, г)
конец

15.

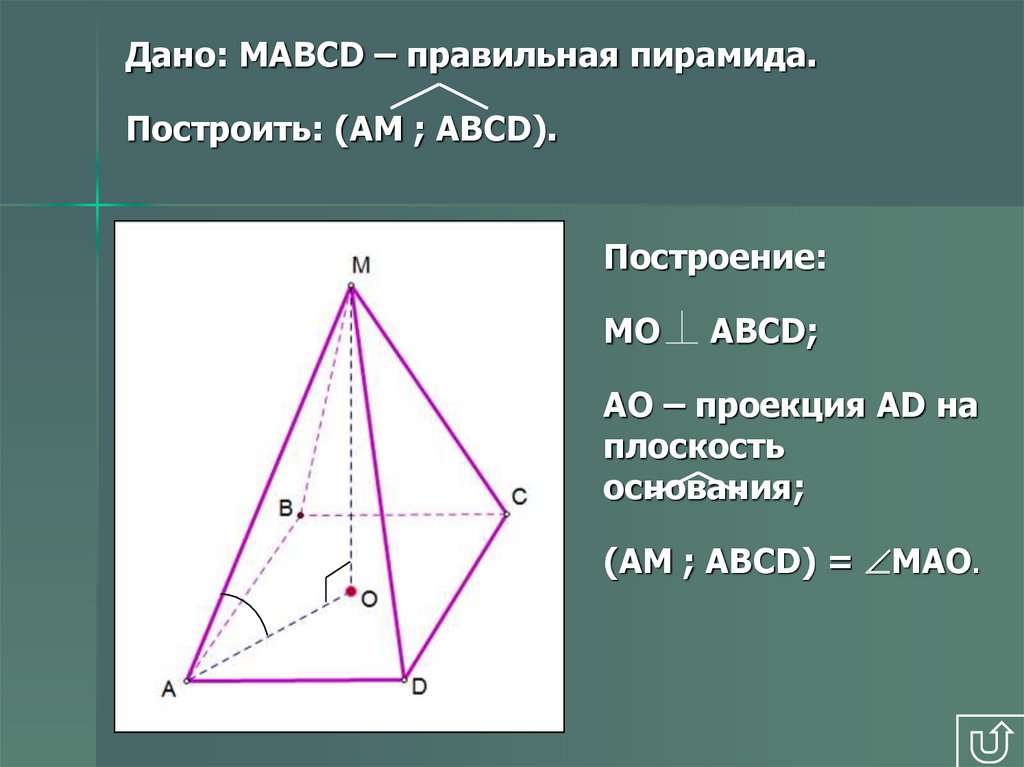
Дано: MAВCD – правильная пирамида.
Построить: (AM ; ABCD).
Построение:
МО
ABCD;
AO – проекция AD на
плоскость
основания;
(AM ; ABCD) = МAO.

16.

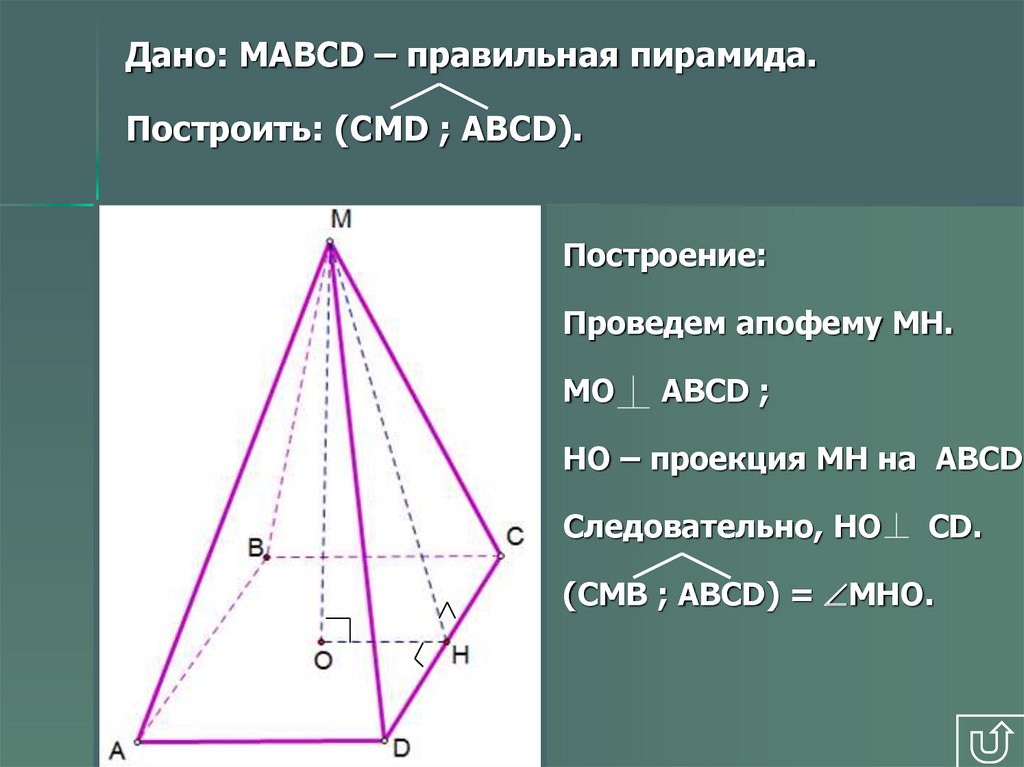
Дано: MAВCD – правильная пирамида.
Построить: (CMD ; ABCD).
Построение:
Проведем апофему МН.
МO
AВСD ;
НО – проекция МН на ABCD.
Следовательно, НО
CD.
(СMВ ; ABCD) = МНО.

17.

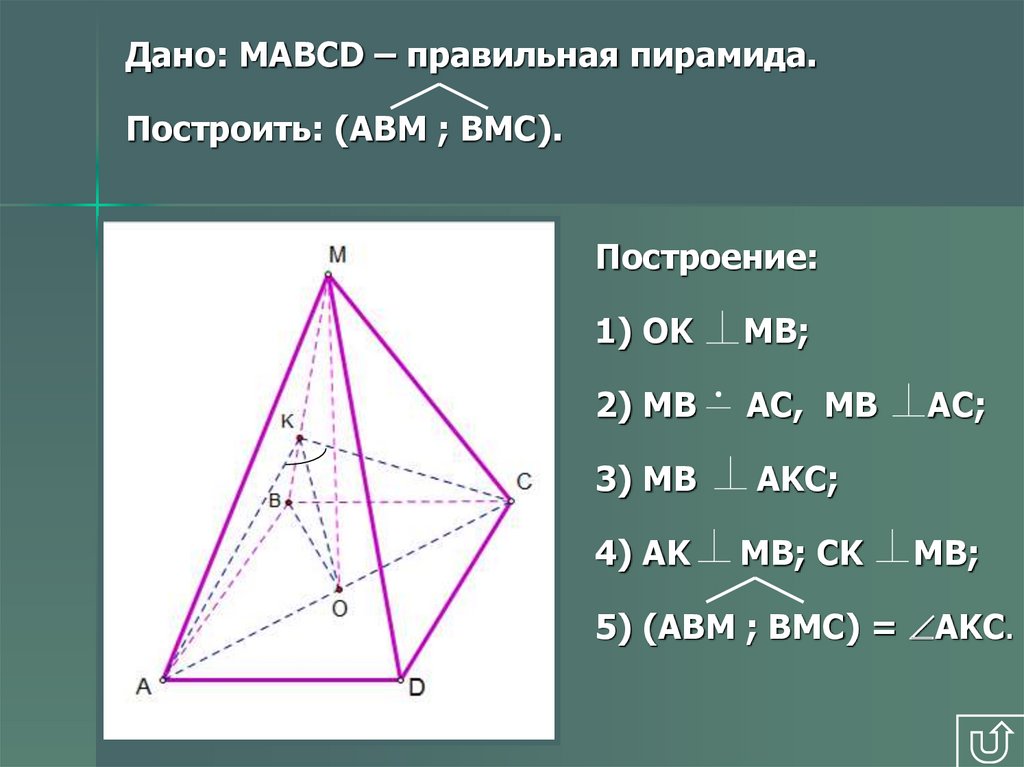
Дано: MAВCD – правильная пирамида.
Построить: (AВM ; BМC).
Построение:
1) OK
MB;
2) MB
AC, MB
3) MB
AKC;
4) AK
MB; CK
AC;
MB;
5) (ABM ; BMC) = AKC.