Похожие презентации:
Решение неравенств методом интервалов. Урок алгебры в 9 классе
1.
МБОУ г.о.Балашиха «Гимназия № 19»Решение неравенств
методом интервалов
урок алгебры в 9 классе
Губарева Регина Николаевна, учитель математики
2.
План применения метода интерваловРазложить многочлен на простые множители;
найти корни многочлена;
изобразить их на числовой прямой;
разбить числовую прямую на интервалы;
определить знаки множителей на интервалах
знакопостоянства;
• выбрать промежутки нужного знака;
• записать ответ (с помощью скобок или знаков
неравенства).
3.
Самостоятельная работаВариант 1.
Вариант 2.
№1. Решите методом интервалов неравенства:
(2 x 5)( x 3) 0;
а) (5 x 2)( x 4) 0;
4 x 2 4 x 3 0.
б) 9 x 2 3x 2 0.
№2. Найдите область определения функции:
y 6 x x 2 3 3 2 x 5.
y 2 7 x x 2 5 5 3x 4.
4.
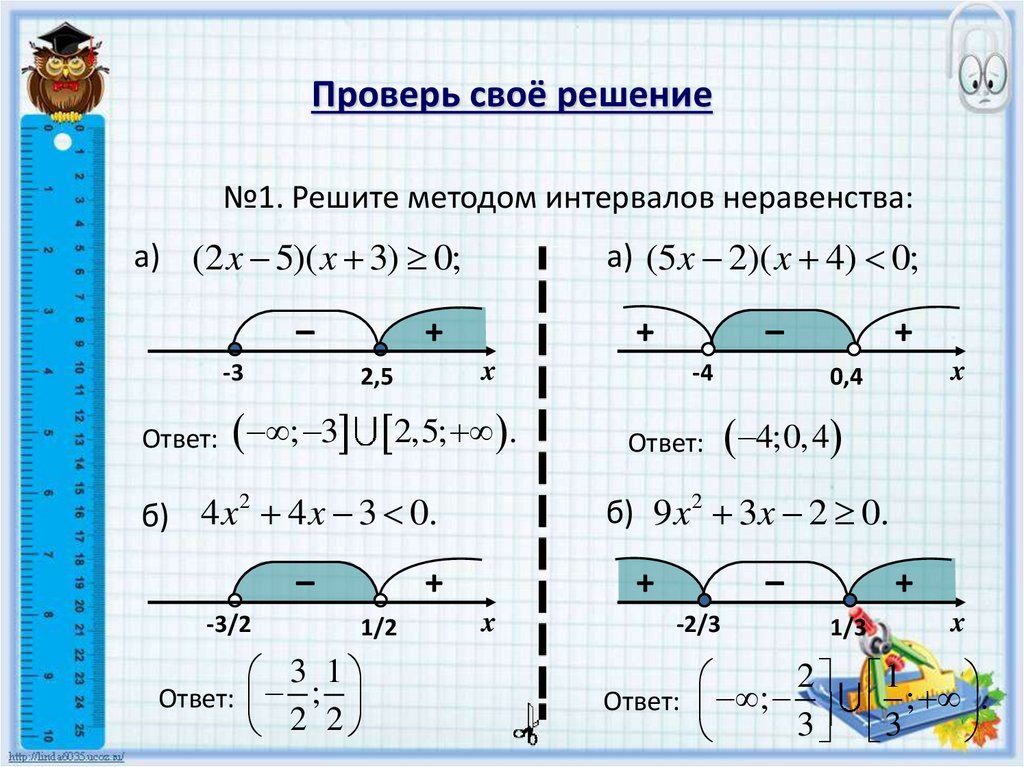
Проверь своё решение№1. Решите методом интервалов неравенства:
а) (2 x 5)( x 3) 0;
–
-3
Ответ:
а) (5 x 2)( x 4) 0;
+
+
x
2,5
; 3 2,5; .
2
б) 4 x 4 x 3 0.
–
-3/2
3 1
Ответ: ;
2 2
-4
Ответ:
+
x
0,4
4;0,4
б) 9 x 2 3x 2 0.
+
1/2
–
+
x
–
-2/3
+
1/3
2
Ответ: ;
3
x
1
;
.
3
5.
Проверь своё решениеВариант 1.
Вариант 2.
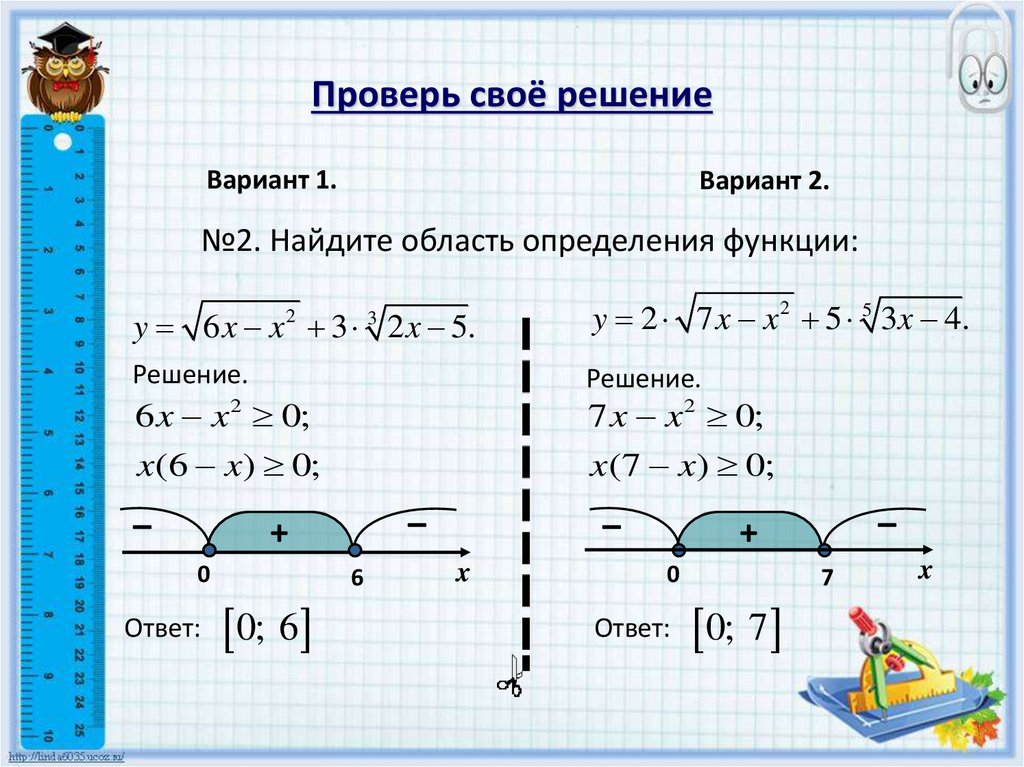
№2. Найдите область определения функции:
y 6 x x 3 2 x 5.
y 2 7 x x 2 5 5 3x 4.
Решение.
Решение.
2
3
6 x x 2 0;
7 x x 2 0;
x(6 x) 0;
–
x(7 x) 0;
–
+
0
Ответ:
0; 6
6
–
x
–
+
0
Ответ:
0; 7
7
x
6.
Оценка самостоятельной работыЗа каждый верно выполненный
пример – поставьте 1 балл.
0 баллов – плохо, «2».
1 балл – удовлетворительно, «3».
2 балла – хорошо, «4».
3 балла – отлично, «5».
7.
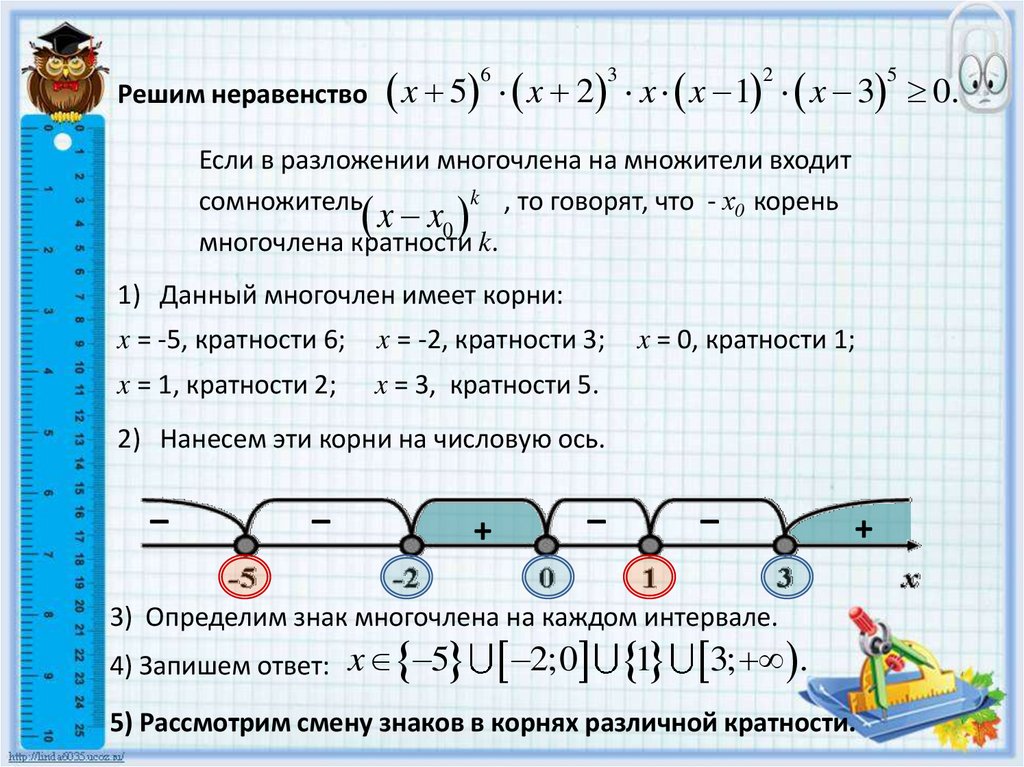
Решим неравенствоx 5 x 2
6
3
x x 1 x 3 0.
2
5
Если в разложении многочлена на множители входит
k , то говорят, что - х корень
сомножитель
0
x x0
многочлена кратности k.
1) Данный многочлен имеет корни:
x = -5, кратности 6;
x = -2, кратности 3;
x = 1, кратности 2;
x = 3, кратности 5.
x = 0, кратности 1;
2) Нанесем эти корни на числовую ось.
–
–
+
–
–
+
3) Определим знак многочлена на каждом интервале.
4) Запишем ответ:
x 5
2;0 1 3; .
5) Рассмотрим смену знаков в корнях различной кратности.
8.
Решите неравенство1 вариант:
x 3 x 2 x 7 x 10 0.
4
5
2
2 вариант:
x 9 x 2 x 6 x 1 0.
2
5
3
Сделайте выводы о смене знака на
интервалах, в зависимости от степени
кратности корня.
9.
Обобщая ваши наблюдения, делаем выводы:1.
Для решения неравенства важно знать, является ли k четным
или нечетным числом.
2. При четном k многочлен справа и слева от х0 имеет один и тот
же знак (знак многочлена не меняется).
3. При нечетном k многочлен справа и слева от х0 имеет
противоположные знаки (знак многочлена изменяется).
10.
Вы можете использоватьданное оформление
для создания своих презентаций,
но в своей презентации вы должны указать
источник шаблона:
Фокина Лидия Петровна
учитель начальных классов
МКОУ «СОШ ст. Евсино»
Искитимского района
Новосибирской области
Сайт http://linda6035.ucoz.ru/
11.
Интернет-ресурсы:Скрепка http://img-fotki.yandex.ru/get/6610/134091466.1c/0_8f975_cc74afe5_S
Линейка http://s1.pic4you.ru/allimage/y2012/08-20/12216/2356155.png
Циркуль http://img-fotki.yandex.ru/get/6619/108950446.113/0_cd1e9_394b9c86_S
Сова http://img-fotki.yandex.ru/get/6419/108950446.114/0_cd212_c7ac5fee_S
Листья http://img-fotki.yandex.ru/get/6623/108950446.115/0_cd23c_44b148c7_S








 Математика
Математика








