Показатели качества устойчивых ЛСС и методы их определения. Точность ЛСС в установившемся режиме

1.

Автоматика и управление
Тема 6. Качество ЛСС
Лекция 7. Показатели качества устойчивых ЛСС и методы их
определения. Точность ЛСС в установившемся режиме при
действии медленноменяющихся входных сигналов.

2.

Качество - обобщенное понятие, определяющее степень
работоспособности устойчивых ЛСС.
степень устойчивости; быстродействие; точность.
6.1. Показатели качества устойчивых ЛСС и методы их
определения
Показатели качества определяются по динамическим
характеристикам АС.
Прямые показатели качества : величина перерегулирования
hm ( ), время регулирования tр (время переходного процесса),
ошибка в установившемся режиме e(t).
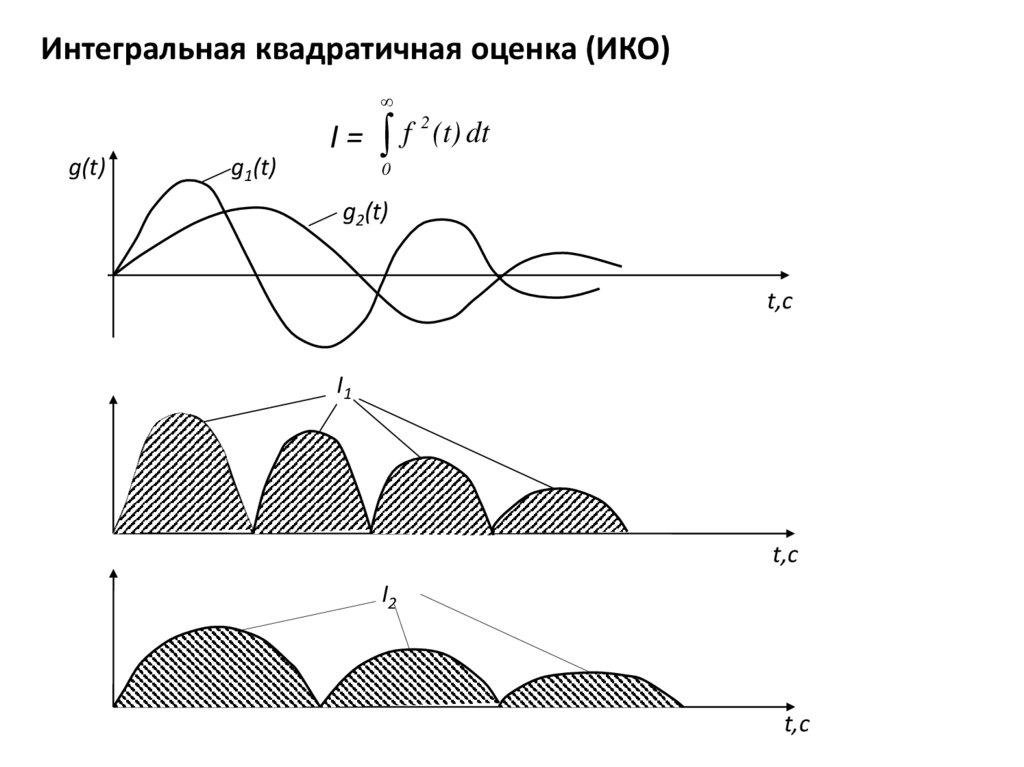
Косвенные: запасы устойчивости 3, L3, интегральные оценки
качества и др.
Различают точные и приближенные методы определения
показателей качества.
Точные методы основаны на анализе переходных процессов
или аналитических выражений передаточных функций АС.

3.

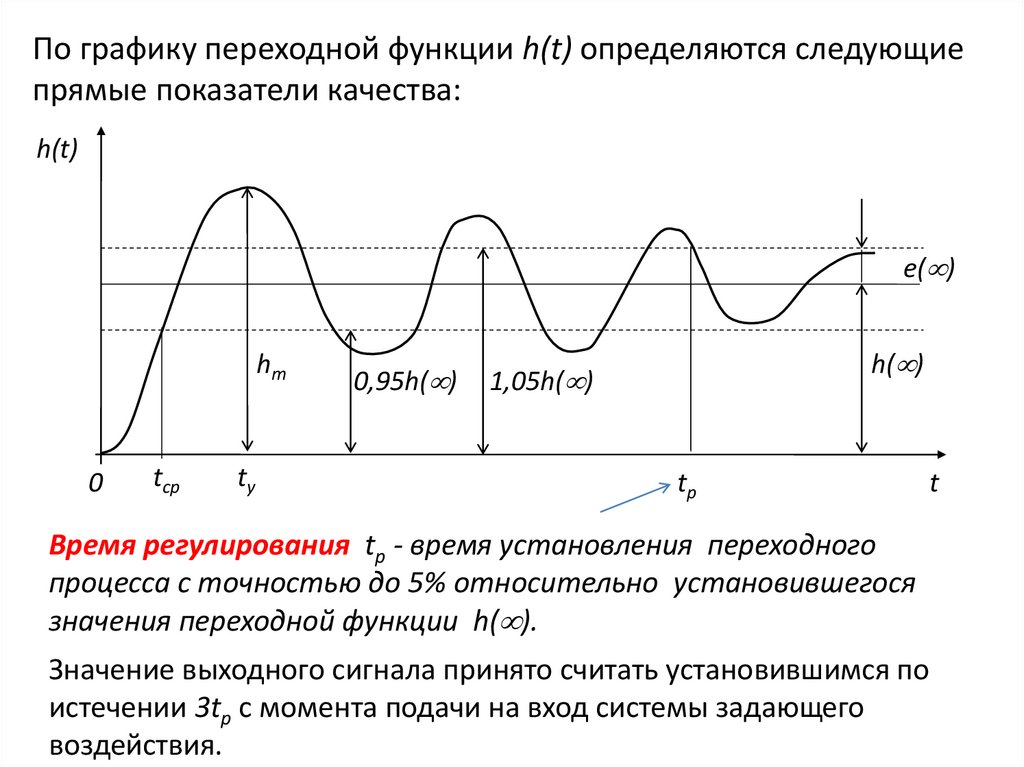
По графику переходной функции h(t) определяются следующие
прямые показатели качества:
h(t)
e( )
hm
0
tcp
ty
0,95h( )
h( )
1,05h( )
tp
t
Время регулирования tр - время установления переходного
процесса с точностью до 5% относительно установившегося
значения переходной функции h( ).
Значение выходного сигнала принято считать установившимся по
истечении 3tр с момента подачи на вход системы задающего
воздействия.

4.

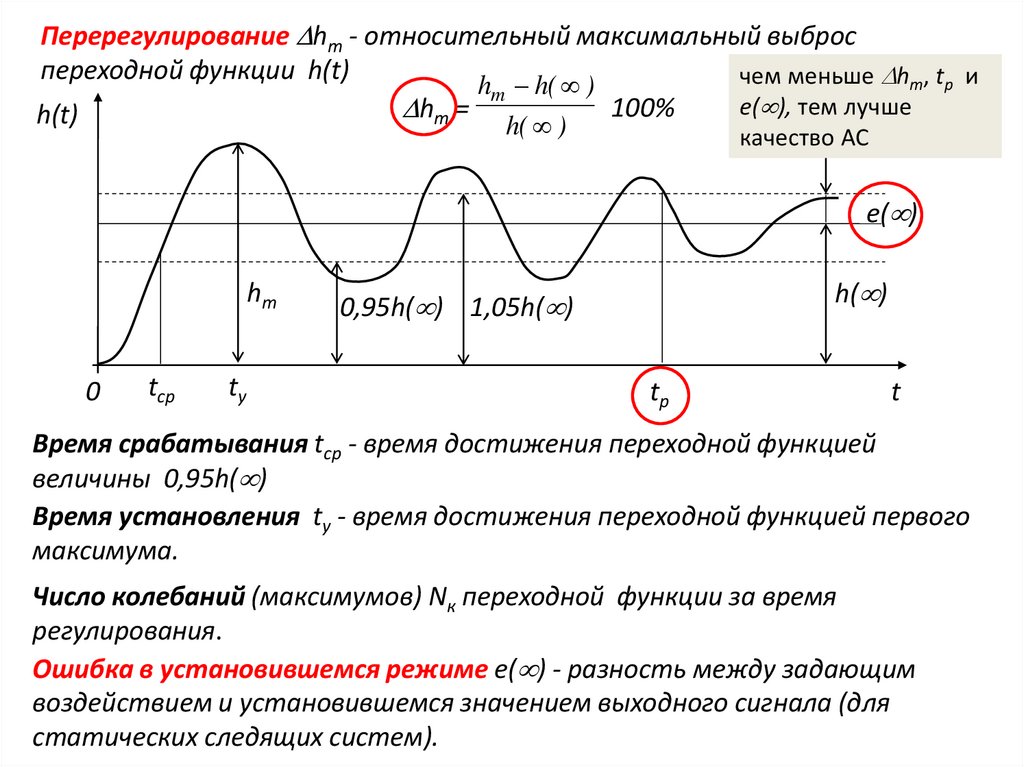
Перерегулирование hm - относительный максимальный выброс
переходной функции h(t)
чем меньше hm, tр и
hm h( )
e( ), тем лучше
100%
hm =
h(t)
h( )
качество АС
e( )
hm
0
tcp
ty
h( )
0,95h( ) 1,05h( )
tp
t
Время срабатывания tср - время достижения переходной функцией
величины 0,95h( )
Время установления tу - время достижения переходной функцией первого
максимума.
Число колебаний (максимумов) Nк переходной функции за время
регулирования.
Ошибка в установившемся режиме e( ) - разность между задающим
воздействием и установившемся значением выходного сигнала (для
статических следящих систем).

5.

Приближенные методы определения показателей качества
основаны на анализе частотных характеристик АС.
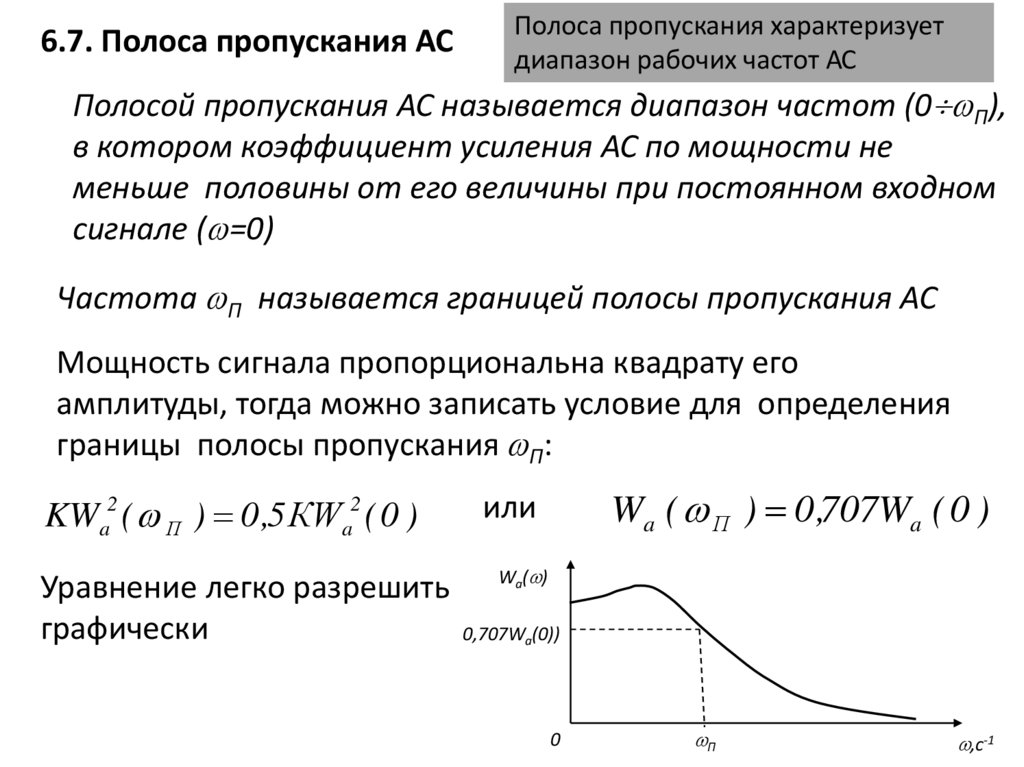
Запасы устойчивости 3 и L3, полоса пропускания п
Важным показателем качества является точность отработки АС
задающего воздействия в установившемся режиме.

6.

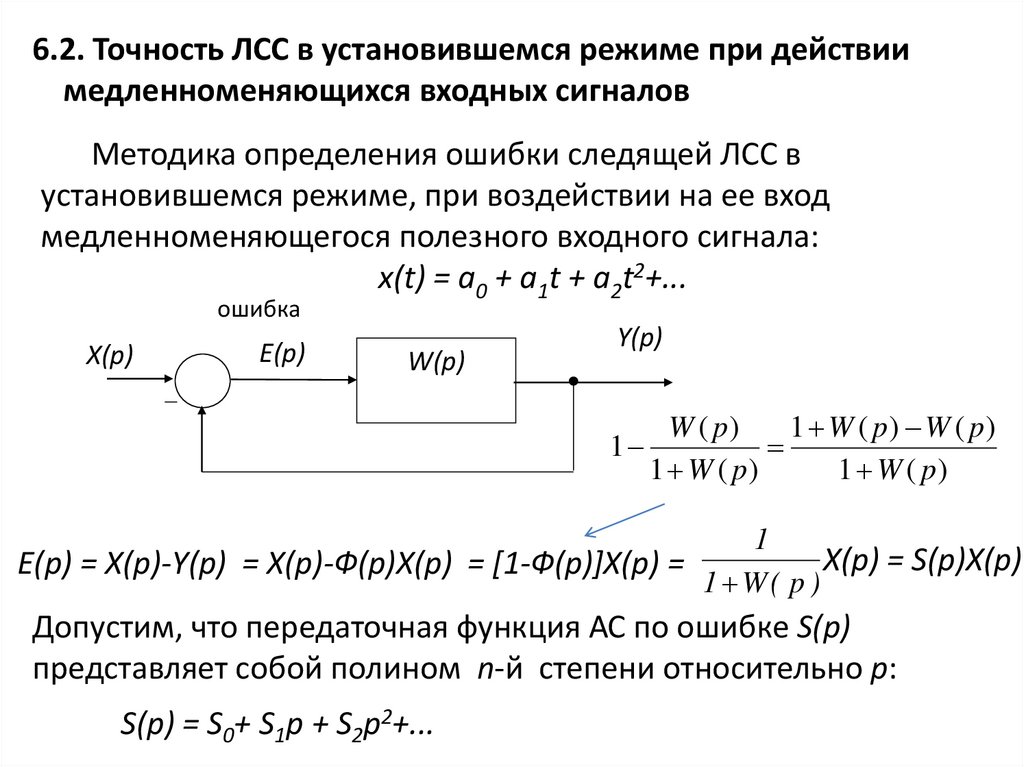
6.2. Точность ЛСС в установившемся режиме при действии
медленноменяющихся входных сигналов
Методика определения ошибки следящей ЛСС в
установившемся режиме, при воздействии на ее вход
медленноменяющегося полезного входного сигнала:
x(t) = a0 + a1t + a2t2+...
ошибка
X(p)
Е(p)
W(p)
Y(p)
W ( p)
1 W ( p) W ( p)
1
1 W ( p)
1 W ( p)
1
X(p) = S(p)X(p)
E(p) = X(p)-Y(p) = X(p)-Ф(p)X(p) = [1-Ф(p)]X(p) =
1 W( p )
Допустим, что передаточная функция АС по ошибке S(p)
представляет собой полином n-й степени относительно p:
S(p) = S0+ S1p + S2p2+...

7.

Ряд Тейлора -
S(p) можно разложить в ряд Тейлора в точке p=0, поскольку S(p)
рациональная функция и точка p=0 не является ее полюсом
2
(а0 0) т.к. АС устойчива:
p
p
S(p) = S(0)+ S(1)(0) +
S(2)(0) +...
2!
1!
(2)
S ( 1 )( 0 )
S
(0 )
Обозначив S(0) = S0;
= S1
=S2, ...
1!
2!
получим S(p) = S + S p + S p2+...
0
1
2
Тогда изображение ошибки системы определится равенством:
E(p) = S(p)X(p) = (S0+S1p+S2p2 +...)X(p) = S0X(p)+S1pX(p)+S2p2X(p)+...
Применив операцию L-1[E(p)]
e(t) = S0x(t)+S1x(1)(t)+S2x(2)(t)+...
Коэффициенты Si , разложения передаточной функции S(p) в
степенной ряд относительно переменной p называются
коэффициентами ошибок.

8.

Как вычислить Si?
S( p )
в m p m в m-1 p m 1 в1 p в0
a n p n a n 1 p n 1 a1 p a0
в m p m в m-1 p m 1 в1 p в0
a n p n a n 1 p n 1 a1 p a0
S0 S1 p S 2 p 2
в m p m в m-1 p m 1 в1 p в0 ( S 0 S 1 p S 2 p 2 )( a n p n a0 );
в m p m в m-1 p m 1 в1 p в0 S 0 a0 ( S 0 a1 S 1 a0 ) p ;
два полинома равны тогда и только тогда, когда равны
коэффициенты при одинаковых степенях аргумента р левой и
правой частей равенства.
Количество коэффициентов
обусловлено минимальным
порядком производной входного
сигнала x(t), равной нулю.
p0
в 0 S 0 a0 S 0
в0
а0
1
p 1 в1 S 0 a1 S 1 a0 S 1 ( в1 а1 S 0 );
а0

9.

Пример: x(t) = t+2t2,
x(1)(t) = 1+4t, x(2)(t) = 4, x(3)(t) = x(4)(t) =...= 0,
следовательно,
число
коэффициентов
ошибок,
подлежащих определению, равно 3: S0, S1, S2,
т.к. ошибка АС в установившемся режиме для такого
сигнала будет определяться равенством:
e(t) = S0x(t)+S1 x(1)(t)+S2 x(2)(t).
Методику можно применить для нахождения выходного
~
сигнала системы y(t), при этом коэффициенты S i
вычисляются из передаточной функции Ф(p).

10.

Пример:
x(t) = 5-6t+7t2;
Ф(p) =
K
T 2 p 2 2T p 1
где T = 1, K = 1, = 0,5
Определим y(t):
~
~ (1)
~ ( 2)
y (t ) S0 x(t ) S1 x (t ) S 2 x (t )
x(1)(t) =-6+14t, x(2)(t) =14,
x(3)(t) =0.
~ ~ ~
необходимо вычислить 3 коэффициента: S 0 , S 1 и S 2
~
~
~
K/( T p 2T p 1 )= S 0 S 1 p S 2 p ;
~ ~
~
K=( T 2 p 2 2T p 1 )( S 0 S 1 p S 2 p 2 );
~
p0
K S 0 Ф(0) 1,
~ ~
~
y(t) = (5-6t+7t2)-(-6+14t) =
p1
0 S 1 S 0 2T S 1 2T K 1,
~
~
~
~
=11-20t+7t2
2 0 S T 2 S 2T S S KT 2 ( 4 2 1 ) 0.
p
0
1
2
2
2
2
2

11.

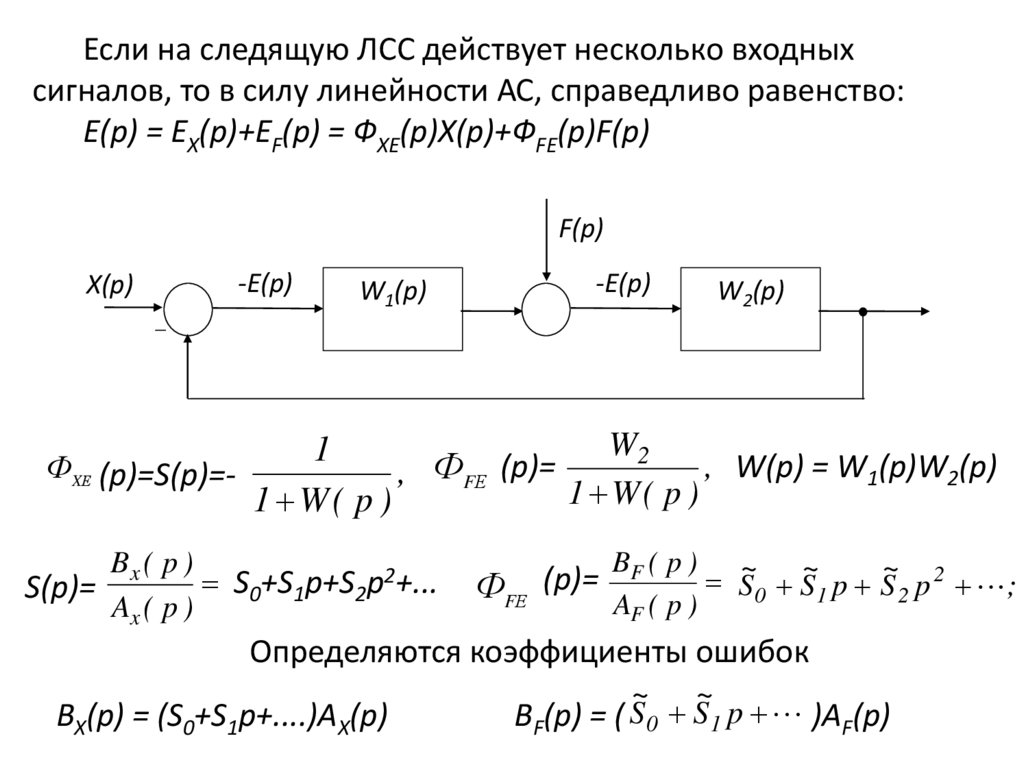
Если на следящую ЛСС действует несколько входных
сигналов, то в силу линейности АС, справедливо равенство:
E(p) = EX(p)+EF(p) = ФXE(p)X(p)+ФFE(p)F(p)
F(p)
X(p)
-Е(p)
-Е(p)
W1(p)
W2(p)
W2
1
, W(p) = W1(p)W2(p)
(p)=
ФXЕ (p)=S(p)=, ФFЕ
1 W( p )
1 W( p )
Bx ( p )
S0+S1p+S2p2+...
S(p)=
Ax ( p )
ФFЕ
(p)=
BF ( p ) ~
S 0 S~1 p S~2 p 2 ;
AF ( p )
Определяются коэффициенты ошибок
BX(p) = (S0+S1p+....)AX(p)
~ ~
S
BF(p) = ( 0 S 1 p )AF(p)

12.

Ошибка системы в установившемся режиме:
e(t) = ex(t)+ef(t)
eх(t)=S0x(t)+S1x(1)(t)+S2x(2)(t)+...-составляющая
задающего сигнала
ошибки
~
~ (1)
~ (2) 2
ef(t) = S 0 f S 1 f p S 2 f
p
- составляющая ошибки от сигнала помехи.
Полученный результат можно обобщить для любого
количества входных сигналов, действующих на ЛСС.
от

13.

6.3. Статические и астатические системы
ЛСС по отношению к входному сигналу x(t) называется
статической, если начальный коэффициент ошибки S0
отличен от нуля:
S0 0
Статическая, по отношению к полезному входному
сигналу, АС - это такая, ошибка которой в установившемся
режиме не равна нулю при постоянном входном сигнале,
т.е., если
x(t) = a = const, то e(t) = S0x(t) 0.
ЛСС по отношению к входному сигналу x(t) называется
астатической -го порядка, если первые
коэффициентов ошибки подряд равны 0, то есть:
S0= 0, S1= 0,...,S -1= 0, S 0.

14.

Например:
S 0 0 ЛСС второго
S 1 0 порядка ас S 2 0 татизма 2;
S 0 0 ЛСС первого поряд
S 1 0 ка астатизма 1;
S 0 0 ЛСС первого
S 1 0 порядка ас S 2 0 татизма 1.
1. Ошибка системы e(t) в установившемся режиме равна 0,
если > k, т.е. e(t) = 0, если > k и описывается полиномом
k
порядка (k- ), если k,
e( t ) ai t i если k
i 0
где k - порядок полинома, описывающего входной сигнал.
2. Чем выше порядок астатизма АС, тем она принципиально
точнее.
3. Ошибка АС тем меньше, чем меньше коэффициенты ошибки.

15.

Основное (необходимое и достаточное)
условие астатизма
ЛСС по отношению к входному сигналу x(t) является
астатической -го порядка тогда и только тогда, когда в
передаточной функции АС по ошибке от этого входного
сигнала:
m
Ф XE ( p)
bi p i
B ( p ) i 0
n
A( p) a p i
i 0
i
имеется дифференцирующих звеньев
~
p B ( p) p (bm p m-ν bν 1 p bν )
Ф XE ( p)
.
n
A( p)
аn p а1 p a0

16.

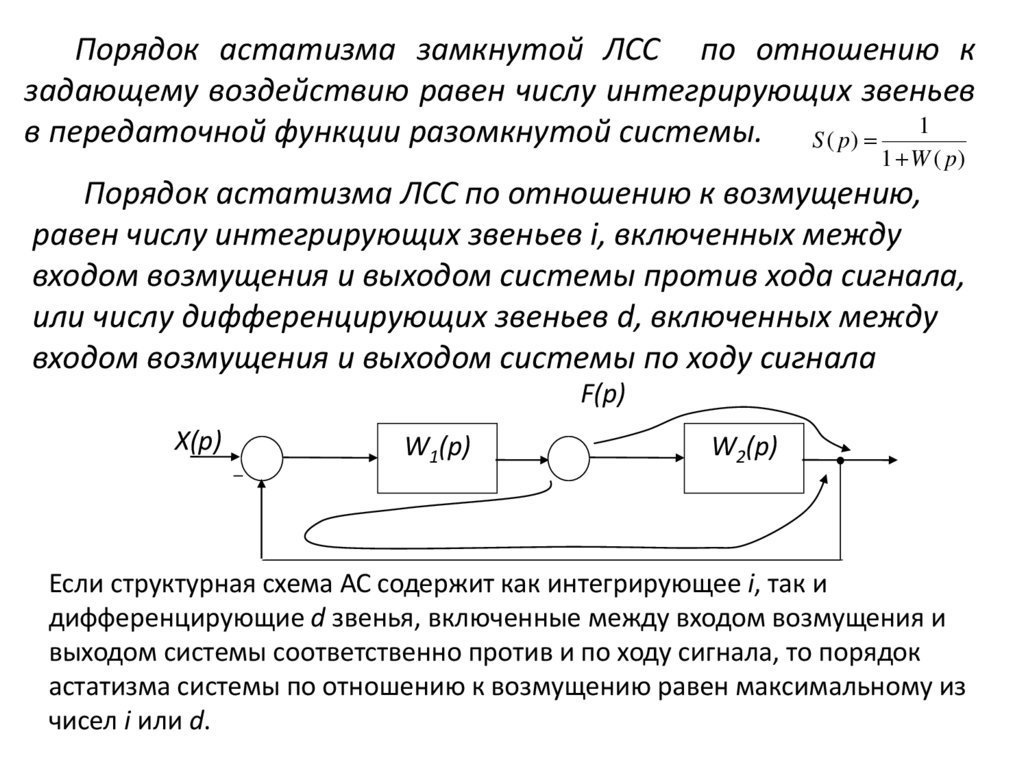
Порядок астатизма замкнутой ЛСС по отношению к
задающему воздействию равен числу интегрирующих звеньев
в передаточной функции разомкнутой системы. S ( p) 1
1 W ( p)
Порядок астатизма ЛСС по отношению к возмущению,
равен числу интегрирующих звеньев i, включенных между
входом возмущения и выходом системы против хода сигнала,
или числу дифференцирующих звеньев d, включенных между
входом возмущения и выходом системы по ходу сигнала
F(p)
X(p)
W1(p)
W2(p)
Если структурная схема АС содержит как интегрирующее i, так и
дифференцирующие d звенья, включенные между входом возмущения и
выходом системы соответственно против и по ходу сигнала, то порядок
астатизма системы по отношению к возмущению равен максимальному из
чисел i или d.

17.

Влияние коэффициента усиления разомкнутой
системы на ошибку ЛСС
Если передаточная функция разомкнутой следящей системы
Е(p)
X(p)
d 0 d1 p d m 1 p m 1 d m p m
W( p )
,
n 1
n
C0 C1 p Cn 1 p Cn p
W(p)
Y(p)
то, передаточная функция по ошибке от задающего воздействия
1
C0 C1 p Cn 1 p n 1 Cn p n
ФXE ( p )
1 W ( p ) (C0 d 0 ) (C1 d1 ) p (Cm d m ) p m Cn p n
с другой стороны
Ф XE ( p) S0+S1p+S2p2+...
Тогда
(C0+C1p+...+Cnpn) = (S0+S1p+...)[(C0+d0)+(C1+d1)p+...+Cnpn],
C0 S0 (d 0 C0 )
p1 C1 S0 (C1 d1 ) S1 (C0 d 0 ) и т.д.
p0
Если АС статическая, то C0 0
1
S0
K 1 e(t ) a
a
K 1
e(t) = S0a =
Пусть C0=1, тогда W(0) = d0=K - коэффициент
усиления разомкнутой системы.
Допустим, что x(t) = a = const.
K 1

18.

Ошибка статической АС в отработке постоянного
входного сигнала уменьшается при увеличении
коэффициента усиления разомкнутой системы.
вывод справедлив не только для статических АС, но и для всех
астатических систем
АС астатичная 1 порядка ( =1). Тогда, согласно основному условию
астатизма, коэффициенты C0=0, а C1 0.
C0 S0 (d 0 C0 )
p0
p1 C1 S0 (C1 d1 ) S1 (C0 d 0 ) и т.д.
Пусть C1 =1, а d0=K. Тогда
Допустим, что x(t) = a0+a1t, тогда
x(1)(t)=a1= const
S0 = 0, S1= 1/K
(1)
x
(t ) a1
(1)
e(t) = S0x(t)+S1x (t) =
K
K
Ошибка астатической системы I порядка в отработке
линейно изменяющегося задающего воздействия равна
отношению скорости изменения входного сигнала к
коэффициенту усиления разомкнутой системы.

19.

Связь коэффициентов ai, вi передаточной функции
замкнутой системы с порядком ее астатизма
Пусть передаточная функция разомкнутой системы:
Тогда передаточная функция
замкнутой системы
d 0 d1 p d m 1 p m 1 d m p m
W( p )
,
n 1
n
C0 C1 p Cn 1 p Cn p
в0 в1 р вm 1 р m 1 вm р m
W(p)
Ф( р )
1 W(p) a0 a1 p an 1 p n 1 an p n
где в0= d0, в1 = d1,..., вm= dm; a0= C0+d0, a1= C1+d1 , ..., am=(Cm+dm ),
..., an= Cn.
Пусть =1, тогдаC0= 0, а C1 0.
Сравнивая коэффициенты ai и вi - a0=в0, а a1 в1 и Ф(р)р=0=1.
Пусть =2, тогда C0=0, C1=0, C2 0. В этом случае очевидно, что в0=а0, в1=а1,
в2 а2.
Порядок астатизма замкнутой АС по отношению к
задающему воздействию определяется числом равных друг
другу первых (с младшими индексами) коэффициентов ai и
вi ее передаточной функции.

20.

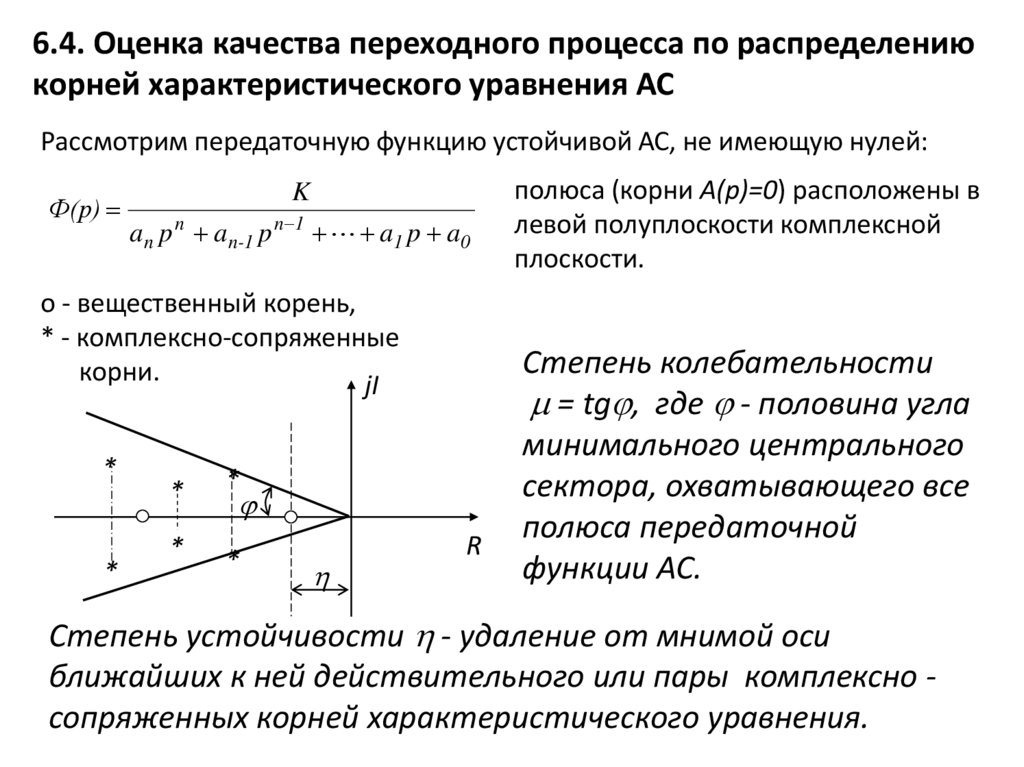
6.4. Оценка качества переходного процесса по распределению
корней характеристического уравнения АС
Рассмотрим передаточную функцию устойчивой АС, не имеющую нулей:
Ф(p)
K
a n p n a n-1 p n 1 a1 p a0
о - вещественный корень,
* - комплексно-сопряженные
корни.
jI
*
*
*
*
*
*
R
полюса (корни A(p)=0) расположены в
левой полуплоскости комплексной
плоскости.
Степень колебательности
= tg , где - половина угла
минимального центрального
сектора, охватывающего все
полюса передаточной
функции АС.
Степень устойчивости - удаление от мнимой оси
ближайших к ней действительного или пары комплексно сопряженных корней характеристического уравнения.

21.

jI
*
*
*
*
*
*
R
Ближайшему к мнимой оси полюсу
соответствует медленно
изменяющаяся составляющая
переходной функции, следовательно,
величина определяет время
регулирования АС. Очень грубо
можно принимать
tp
3
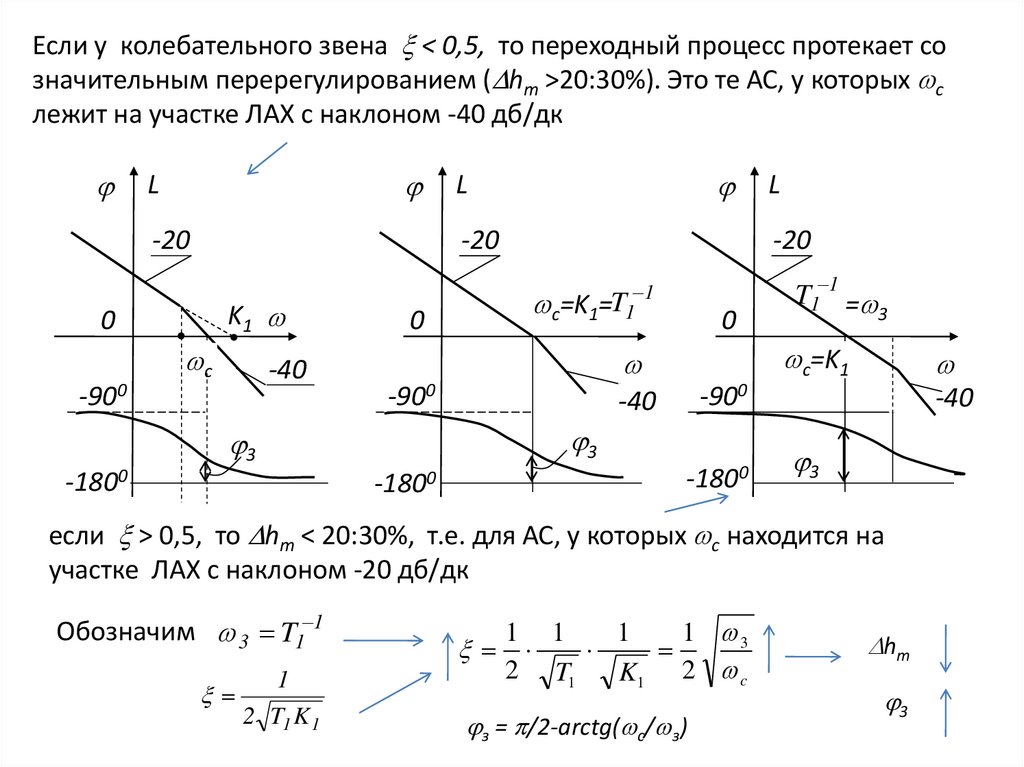
Степень колебательности = tg тесно связана с перерегулированием
АС hm . Если два полюса системы комплексно-сопряженные, а остальные
действительные, то
hm e- / 100% - формула Фельдбаума А.А.
В общем случае данная зависимость позволяет оценить верхнюю
границу перерегулирования. Из нее следует, что для уменьшения hm
необходимо уменьшить (т.е. угол ).
При наличии нулей в передаточной функции АС их расположение на
комплексной плоскости необходимо также учитывать при оценке качества
переходного процесса. В частности, чем ближе они расположены к мнимой
оси, тем больше hm

22.

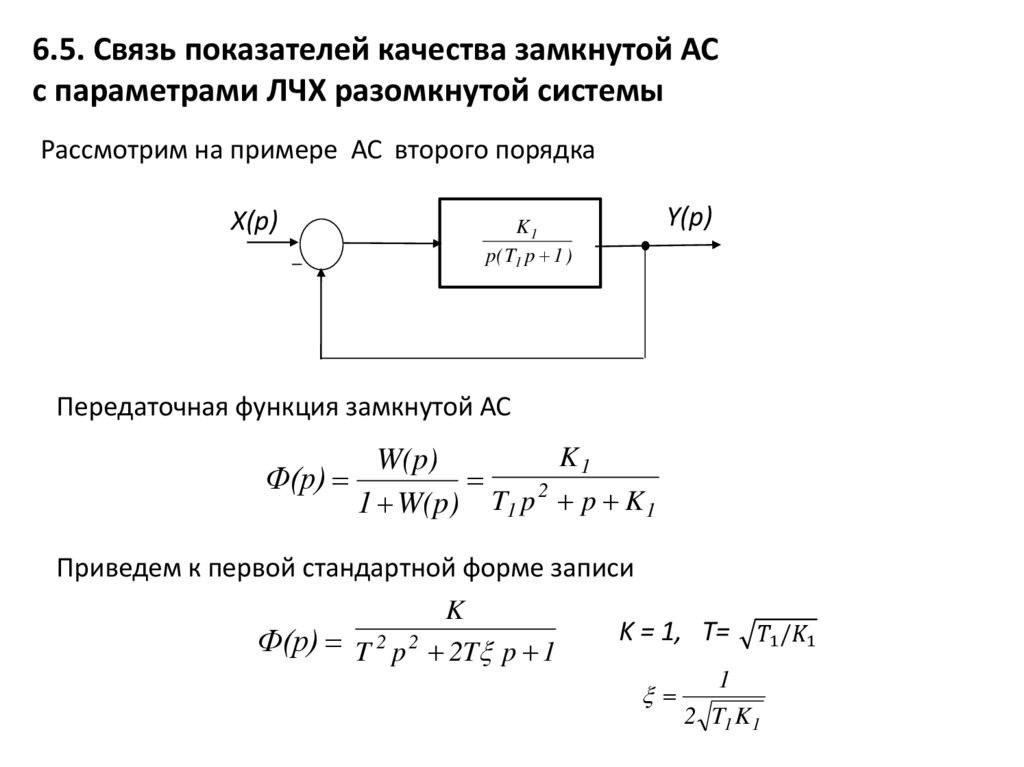
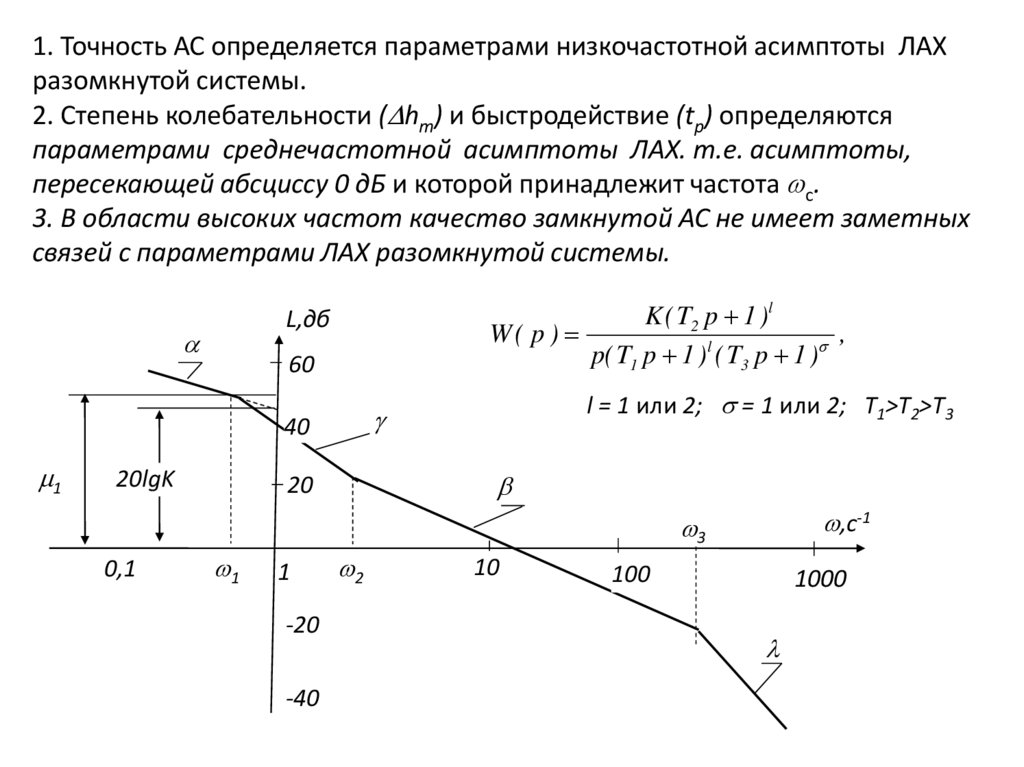
6.5. Связь показателей качества замкнутой АС
с параметрами ЛЧХ разомкнутой системы
Рассмотрим на примере АС второго порядка
X(p)
Y(p)
K1
p( T1 p 1 )
Передаточная функция замкнутой АС
K1
W(p)
Ф(p)
2
1 W(p) T1 p p K 1
Приведем к первой стандартной форме записи
K
K = 1, T=