Числовые функции

1.

ЧИСЛОВЫЕ ФУНКЦИИ
Учитель математики :
Горожанкина С.Я.
Автор проекта: Михирева Е.С.
9 класс

2.

Впервые функция вошла в математику под именем
«переменная величина» в знаменитом труде
французского математика и философа Рене
Декарта «Геометрия» (1637 г.)

3.

Термин «функция»
впервые встречается у
немецкого математика
Лейбница в 1694 г.
В употребление термин
был введен в начале XVIII
века Иоганном Бернулли

4.

УСТНАЯ
РАБОТА

5.

ОПРЕДЕЛЕНИЕ.
ЕСЛИ ДАНЫ ЧИСЛОВОЕ МНОЖЕСТВО Х
И ПРАВИЛО F, ПОЗВОЛЯЮЩЕЕ
ПОСТАВИТЬ В СООТВЕТСТВИЕ КАЖДОМУ
ЭЛЕМЕНТУ Х ИЗ МНОЖЕСТВА Х
ОПРЕДЕЛЕННОЕ ЧИСЛО У, ТО ГОВОРЯТ
ЗАДАНА ФУНКЦИЯ
У
=
F
(
X
)
С
ОБЛАСТЬЮ ОПРЕДЕЛЕНИЯ
ПИШУТ У = F (X) , Х Х
Х;
Переменную х называют независимой
переменной или аргументом, а переменную
у – зависимой переменной или функцией

6.

Определение 2.
Множество всех значений х
называют областью
определения
функции и обозначают D(f)
ОПРЕДЕЛЕНИЕ 3.
МНОЖЕСТВО ВСЕХ ЗНАЧЕНИЙ
ФУНКЦИИ У = F (X) , Х Х,
НАЗЫВАЮТ ОБЛАСТЬЮ
ЗНАЧЕНИЙ ФУНКЦИИ И
ОБОЗНАЧАЮТ Е(F)

7.

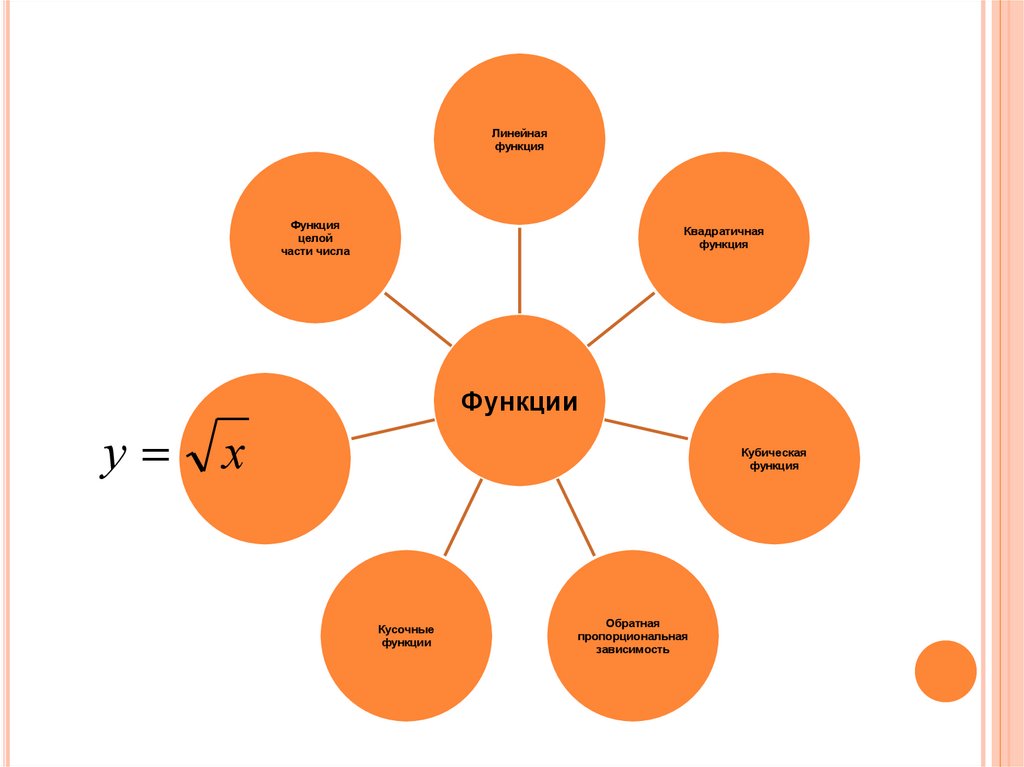
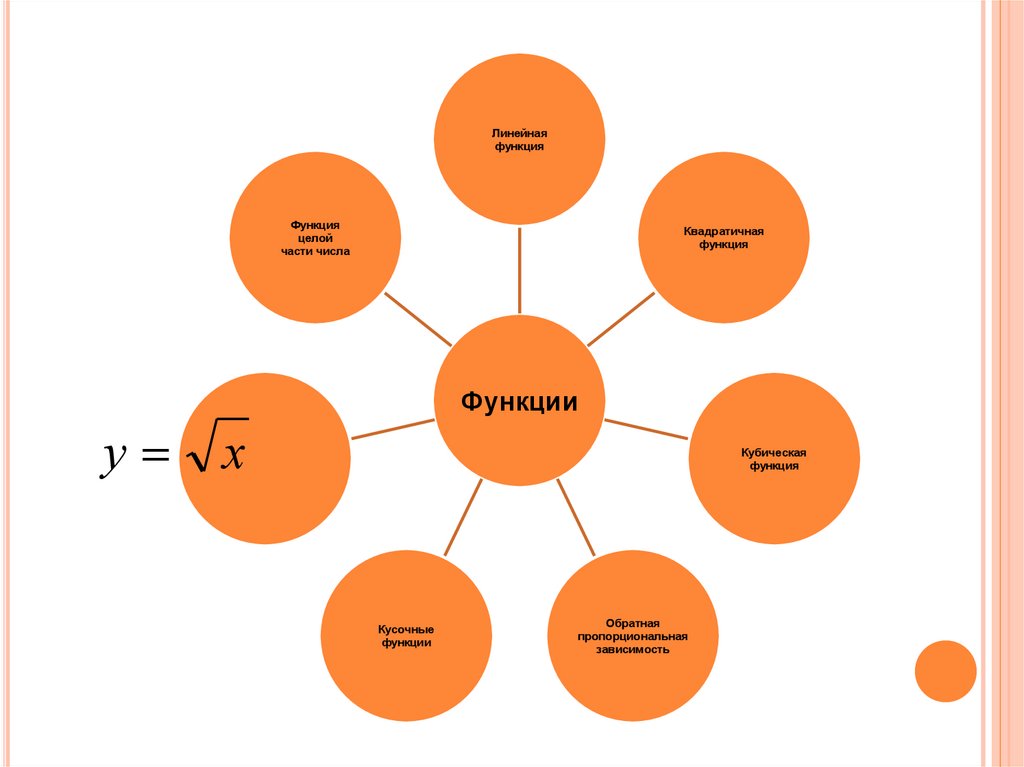
Линейная
функция
Функция
целой
части числа
Квадратичная
функция
Функции
у
х
Кубическая
функция
Кусочные
функции
Обратная
пропорциональная
зависимость

8.

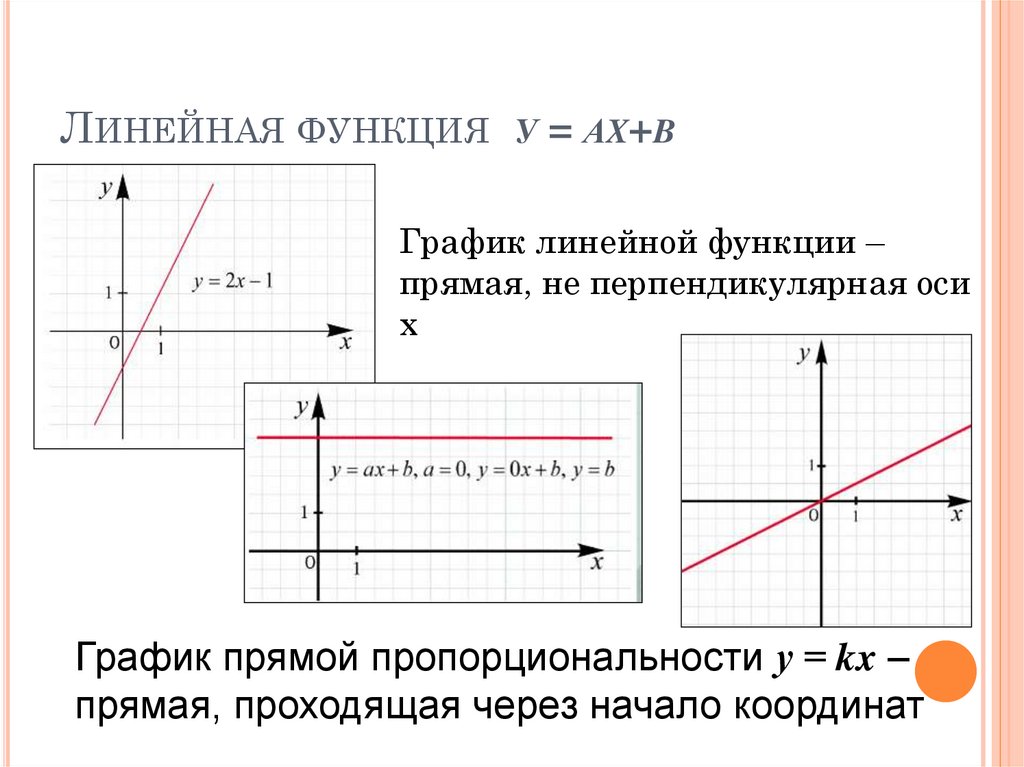
ЛИНЕЙНАЯ ФУНКЦИЯ
У
= АX+B
График линейной функции –
прямая, не перпендикулярная оси
х
График прямой пропорциональности у = kx –
прямая, проходящая через начало координат

9.

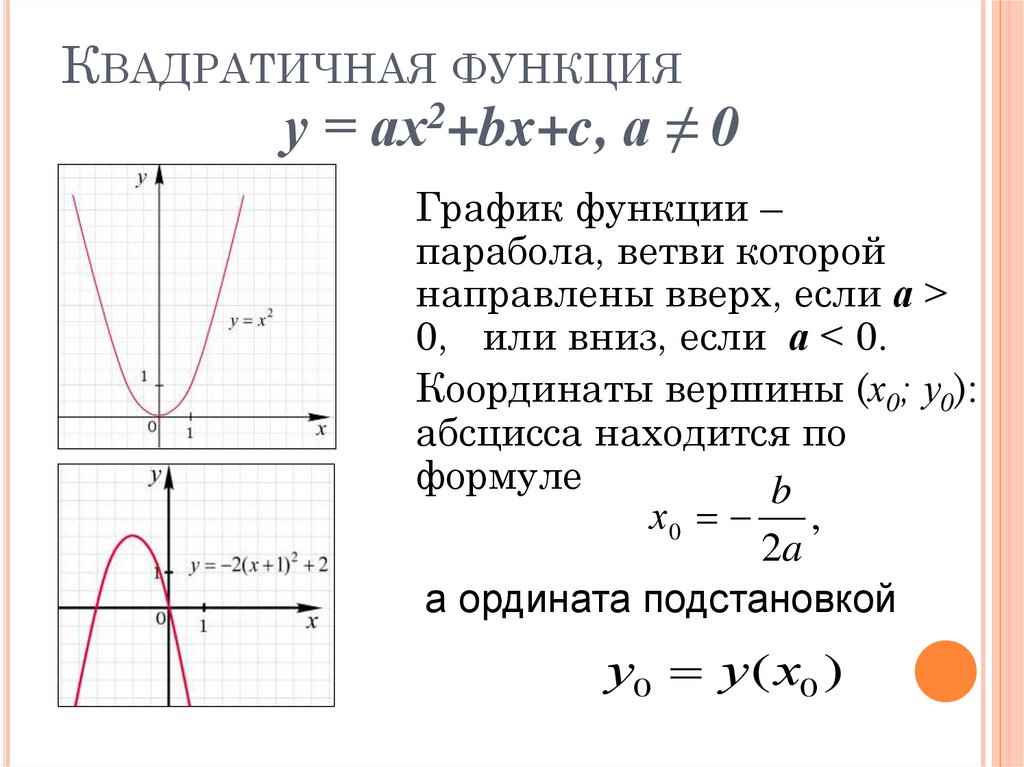
КВАДРАТИЧНАЯ ФУНКЦИЯ
у = ах2+bx+c, а ≠ 0
График функции –
парабола, ветви которой
направлены вверх, если а >
0, или вниз, если а < 0.
Координаты вершины (х0; у0):
абсцисса находится по
формуле
b
х0 ,
2a
а ордината подстановкой
у0 у( х0 )

10.

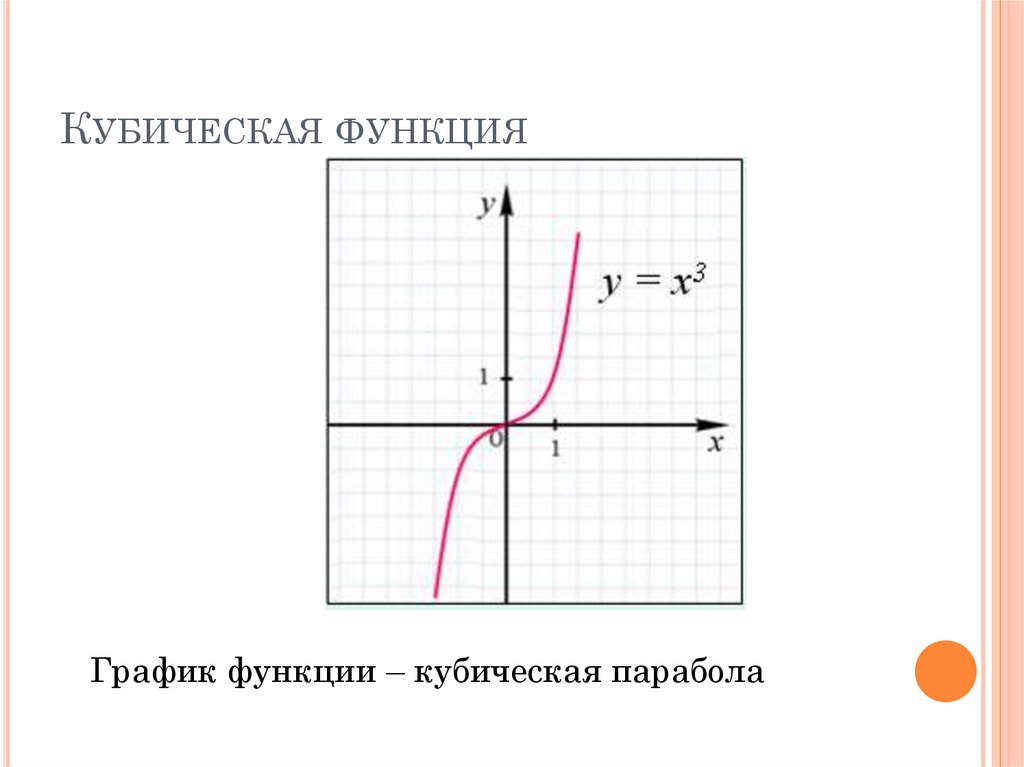
КУБИЧЕСКАЯ ФУНКЦИЯ
у = х3
График функции – кубическая парабола

11.

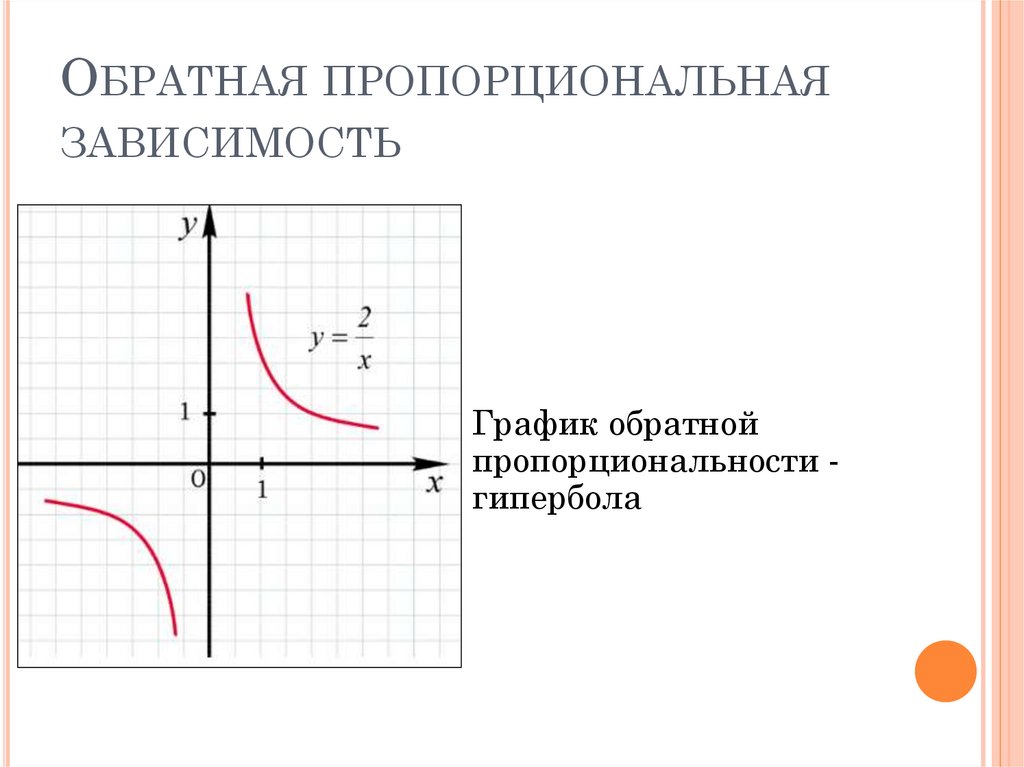
ОБРАТНАЯ ПРОПОРЦИОНАЛЬНАЯ
ЗАВИСИМОСТЬ
График обратной
пропорциональности гипербола

12.

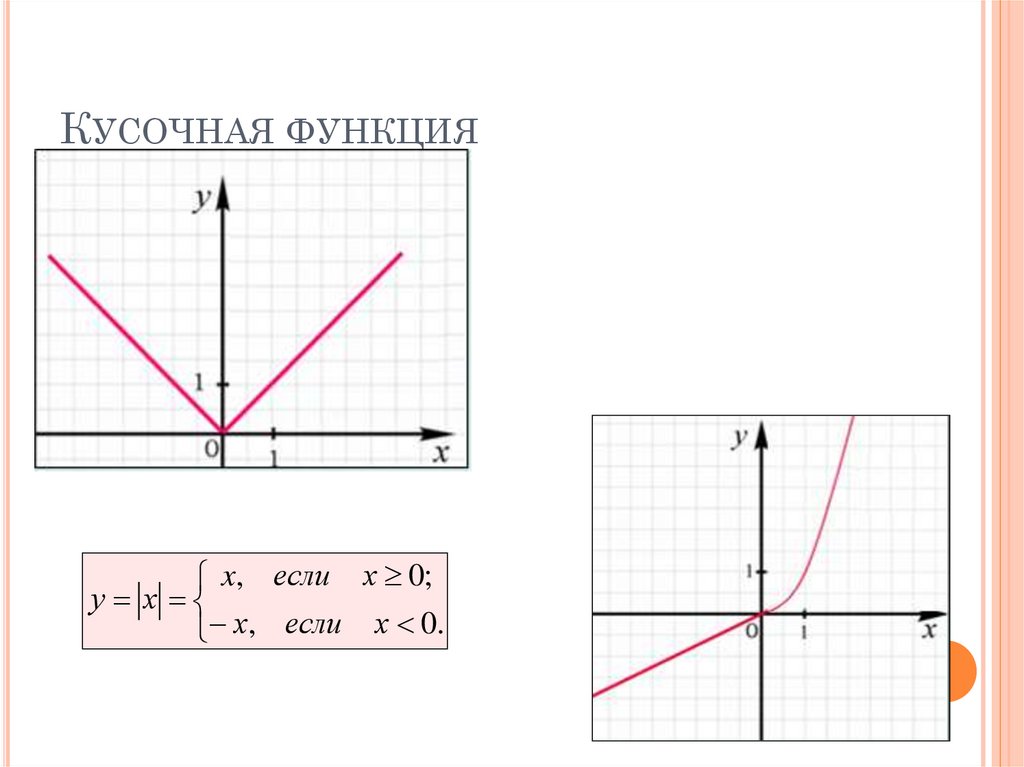
КУСОЧНАЯ ФУНКЦИЯ
x 2 , если х 0;
у
0,5 х, если х 0.
x, если х 0;
у х
х, если х 0.

13.

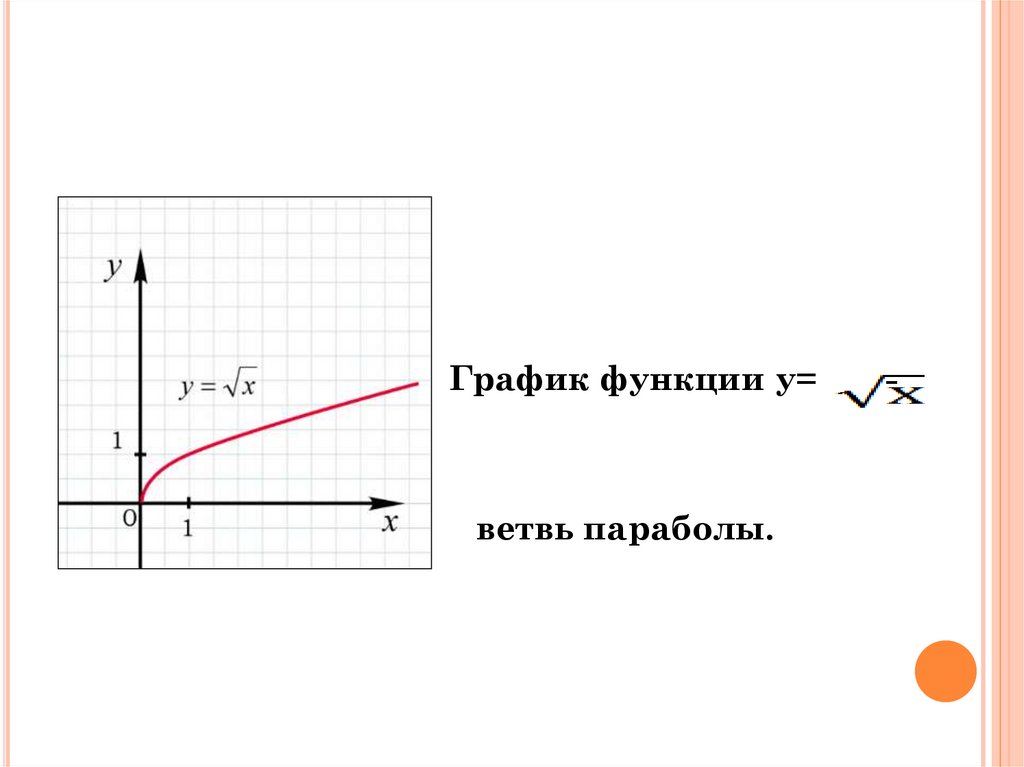
График функции у=
ветвь параболы.
-

14.

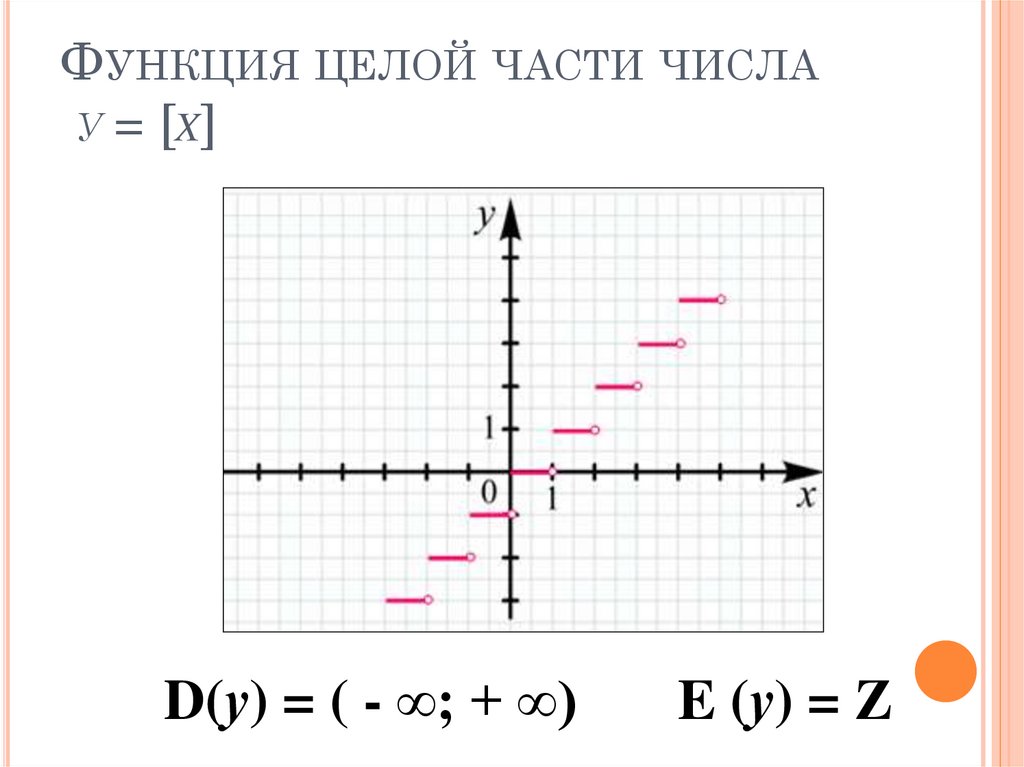
ФУНКЦИЯ ЦЕЛОЙ ЧАСТИ ЧИСЛА
У = [X ]
D(у) = ( - ∞; + ∞)
E (у) = Z

15.

Линейная
функция
Функция
целой
части числа
Квадратичная
функция
Функции
у
х
Кубическая
функция
Кусочные
функции
Обратная
пропорциональная
зависимость

16.

Аналитический
Графический

17.

у
х 2
Аналитический способ
задания функции – это значит
указать формулу или
несколько формул, которые
позволят по произвольно
выбранному значению х из
D(f) вычислить
соответствующее значение у
у 2х 3 1
x 2 , если х 0;
f ( x) х 1, если 0 х 2;
3, если 2 х 4.
g ( x) x 3

18.

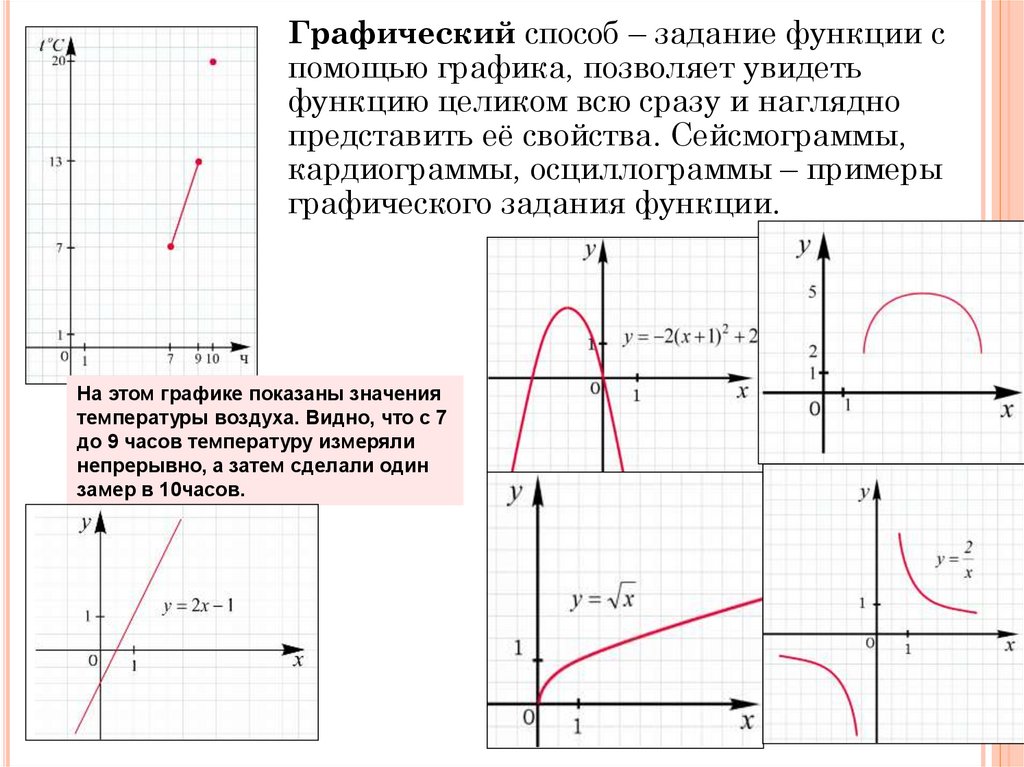
Графический способ – задание функции с
помощью графика, позволяет увидеть
функцию целиком всю сразу и наглядно
представить её свойства. Сейсмограммы,
кардиограммы, осциллограммы – примеры
графического задания функции.
у 9 ( х 5) 2 2
На этом графике показаны значения
температуры воздуха. Видно, что с 7
до 9 часов температуру измеряли
непрерывно, а затем сделали один
замер в 10часов.

19.

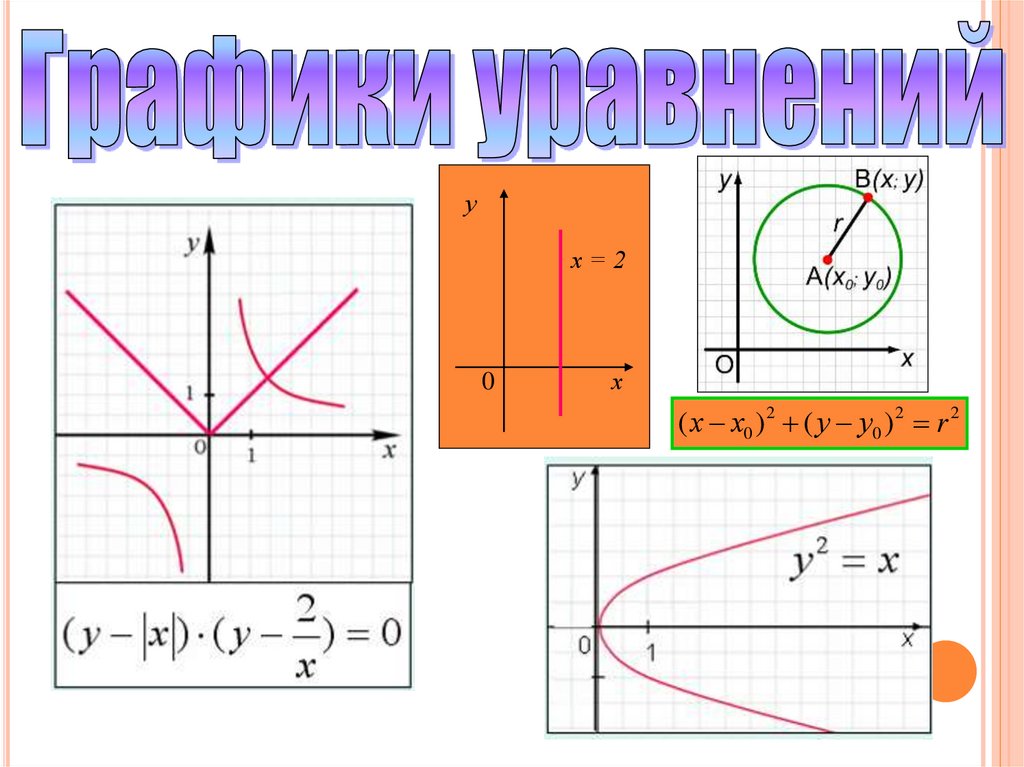
у
х=2
0
х
( х х0 ) 2 ( у у0 ) 2 r 2

20.

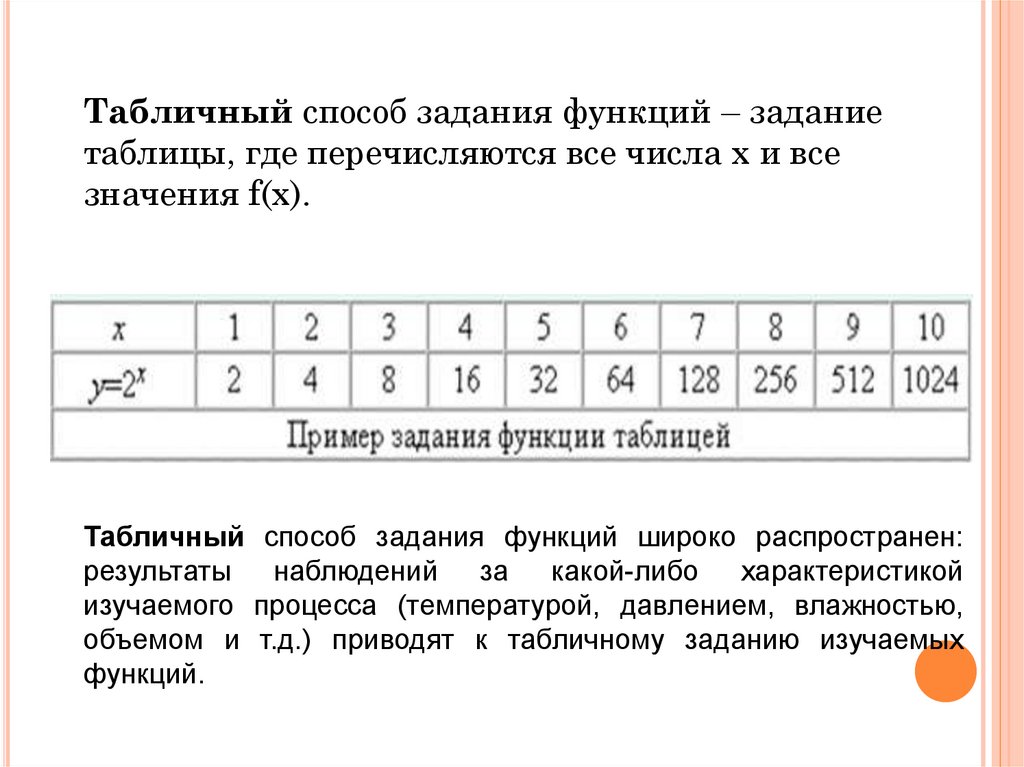
Табличный способ задания функций – задание
таблицы, где перечисляются все числа х и все
значения f(х).
Табличный способ задания функций широко распространен:
результаты наблюдений за какой-либо характеристикой
изучаемого процесса (температурой, давлением, влажностью,
объемом и т.д.) приводят к табличному заданию изучаемых
функций.

21.

Словесный способ задания функций –
правило задания функции описывается
словами
Например, так: у – это число, которое
получится, если у натурального числа х
стереть первую цифру. Чтобы получить
значение такой функции, нужно сначала
задать значение аргумента – написать число
х. Затем, в соответствии с описанием нужно
стереть первую цифру. Если после нее
окажутся нули, их тоже нужно стереть.
Получившееся число и будет значением
функции.

22.

САМОСТОЯТЕЛЬНАЯ
РАБОТА
1.
2.
Найдите область
2х
определения
у
3х 18
функции
Лежит ли точка А (3;7) на
графике функции
у = -х2 + 4х + 4?
3.
4.
5.
Проходит ли прямая,
заданная уравнением
у = 5х + 2, через четвертую
координатную четверть?
Найдите область значения
функции у = (х -2)2 - 3.
Функция задана
уравнением у = 4х – 5.
Какая линия служит
графиком этой функции?
1. Найдите область
определения
у 2х 8
функции
2. Лежит ли точка В ( 2;-5) на
линии, заданной
уравнением у = -х2+ 2х - 9?
3. Проходит ли прямая,
заданная уравнением
у = -3х – 5, через третью
координатную четверть?
4. Найдите область значения
функции у = - 2(х +1)2 + 3.
5. Функция задана
уравнением у = (- 2/7) х +5.
Какая линия служит
графиком этой функции?

23.

ОТВЕТЫ
1.
2.
Найдите область
D (y): х > 6 или 2 х
определения
у
функции
D (y)= ( 6; + ∞ ) 3х 18
Лежит ли точка А (3;7) на
Да
графике функции
у = -х2 + 4х + 4?
3.
4.
5.
Нет
Проходит
ли прямая,
заданная уравнением
у = 5х + 2, через четвертую
координатную четверть?
Е(у): у ≥область
-3 илизначения
Найдите
Е(у)= [-3;
функции
у =+(х∞)-2)2 - 3.
Функция
Прямаязадана
уравнением у = 4х – 5.
Какая линия служит
графиком этой функции?
1. Найдите область
D (y): х ≤ 4 или
определения
у 2х 8
функции
D (y)= (- ∞; 4]
2. Лежит ли точка В ( 2;-5) на
Нет
линии, заданной
уравнением у = -х2+ 2х - 9?
3. Проходит
ли прямая,
Да
заданная уравнением
у = -3х – 5, через первую
координатную четверть?
4. Найдите
область
Е(у): у ≤
3 илизначения
функции
= - 3]
2(х +1)2 + 3.
Е(у)= ( -у ∞;
5. Функция задана
Прямая
уравнением у = (- 2/7) х +5.
Какая линия служит
графиком этой функции?

24.

ТЕМА: «ЧИСЛОВЫЕ ФУНКЦИИ»
Вывод.
Недостаточно лишь понять задачу,
необходимо желание решить её. Без
сильного желания решить трудную
задачу невозможно, но при наличии
такового – возможно. Где есть
желание, найдётся путь!
Пойа Д.

25.

Спасибо
за
внимание!!
!