Похожие презентации:
Виды энергии молекул. Спектроскопия как метод регистрации изменения энергии частиц. Лекция 11
1. Лекция 11
Виды энергии молекул. Спектроскопия как методрегистрации изменения энергии частиц. Виды и
основные понятия молекулярной спектроскопии.
Вероятность переходов. Вращательная энергия и
вращательные спектры двухатомных молекул. Задача
о жестком ротаторе. Микроволновая спектроскопия
Понятие о правилах отбора
2. Введение Классификации
Спектроскопия представляет собой широкую область с многочисленными
направлениями исследований, классифицируемыми по типам
исследуемых объектов.
АТОМЫ
МОЛЕКУЛЫ
КРИСТАЛЛЫ
ЯДРА
Атомная спектроскопия
•Атомно-абсорбционная
спектроскопия (ААС)
•Атомно-эмиссионная
спектроскопия с микроволновой
плазмой (МП-АЭС)
•Оптико-эмиссионная
спектроскопия с индуктивносвязанной плазмой (ИСП-ОЭС)
•Масс-спектрометрия с индуктивносвязанной плазмой (ИСП-МС)
Молекулярная спектроскопия
•Спектроскопия в УФ- и
видимой области
•Спектроскопия в УФ-, видимой
и ближней ИК-области
•ИК-спектроскопия с Фурьепреобразованием
•Флуоресцентная
спектроскопия
• Рентгеновская
кристаллография
• Ядерный магнитный
резонанс
3. Спектроскопия охватывает совокупность методов, которые имеют общие принципы, но в тоже время обладает своей спецификой, они
применяются во многих областях науки итехники в аналитических целях и исследованиях
различного рода объектов и процессов. Круг
решаемых этими методами задач весьма широк и
включает
атомную
и
молекулярную
спектроскопию, изучение физических эффектов
и явлений, связанных с излучением
4.
• Особое место в ряду разнообразныхфизико-химических методов занимают
спектральные методы, в частности
молекулярная спектроскопия, которая
широко используется как для качественного
и количественного анализа веществ, так и
для изучения строения вещества и молекул
5. Молекулярная спектроскопия Общие положения
Объединение атомов в молекулы
создает уникальные энергетические
состояния и, как следствие,
уникальные спектры переходов
между состояниями.
Молекулярные спектры могут быть
связаны с различными:
• Спиновыми состояниями электронов
Молекулярная спектроскопия
Применение
Спектроскопия в
УФ- и видимой
области
Изучает взаимодействия между
веществом и энергией
электромагнитного излучения в
ультрафиолетовом, видимом и
ближнем ИК-диапазоне
ИК-спектроскопия с
Фурьепреобразованием
Изучает взаимодействия между
веществом и энергией
электромагнитного излучения в
инфракрасном диапазоне
Флуоресцентная
спектроскопия
Изучает излучение электромагнитной
энергии после взаимодействия между
веществом и энергией
электромагнитного излучения, как
правило, в ультрафиолетовом и
видимом диапазоне
• Вращательными состояниями молекул
• Колебательными состояниями молекул
• Электронными состояниями
Содержание
6.
Молекулярная спектроскопияОбласти электромагнитного излучения
Рентген
γ-излучение
УФ
Видимый диапазон ИК
Микроволны
Радиоволны
16
7.5x10 4.3x10
10
6
2.5x10
10
λ (нм)
-3
10
380
780
6
8
10 10
6
2
3,3
1,6
-3
-5
ν (с-1)
20
10
10
10
ω (см-1) 10
Е (эВ) 10
10
14
4
14
11
9
10 10
4
1.3x10 10 0,1
10 10
6
7. Взаимосвязь спектроскопических методов и областей электромагнитного спектра
λ, мСпектральная
область
Тип квантового перехода
10-12-10-13
γ-излучение
Возбуждение
ядерные реакции
10-8-10-12
Рентгеновское
излучение
Возбуждение
электронов
внутренних Рентгеновская
спектроскопия
10-5-10-8
УФ излучение, Возбуждение
видимое
электронов
излучение,
ближняя ИК
область
валентных Абсорбционная,
эмиссионная,
флуоресцентная
спектроскопия
10-3-10-6
ИК излучение
колебания Инфракрасная
спектроскопия
10-1-10-3
Микроволново Вращение молекул
е излучение
Более 10-1
Радиоволны
Вращение
молекул
и
Спектроскопические
методы
ядер, Ядерно-физические
Микроволновая
спектроскопия
Неспаренные электроны в Электронный
магнитном поле
парамагнитный резонанс
Ядерные
спины
магнитном поле
в Ядерный
резонанс
магнитный
8.
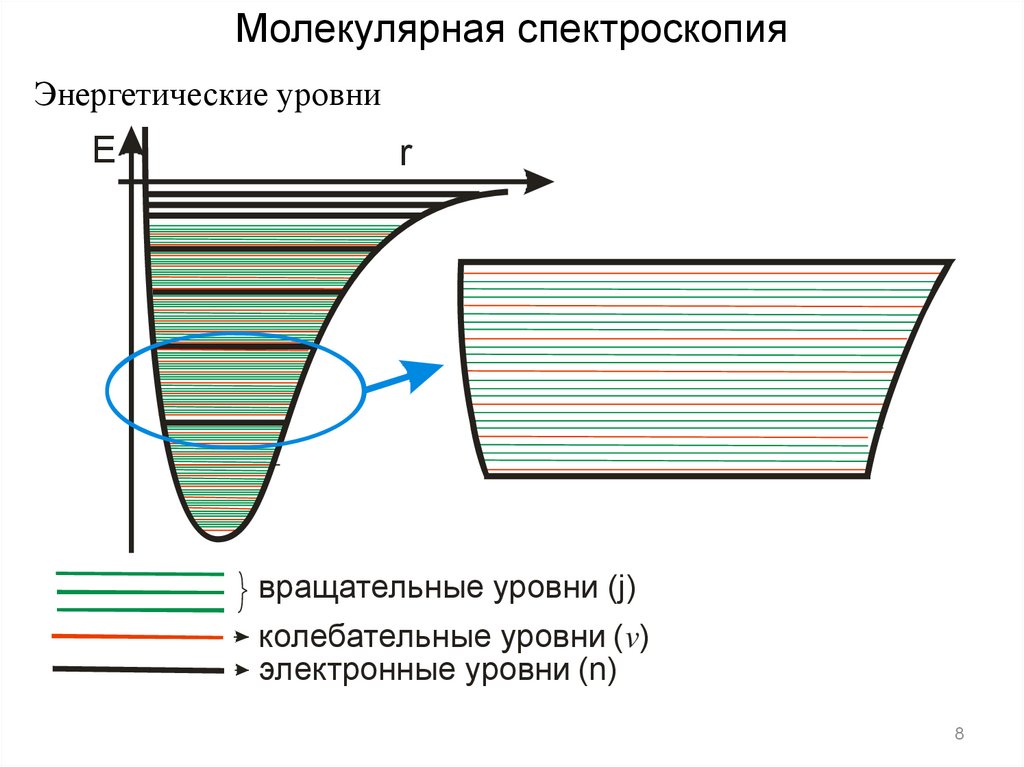
Молекулярная спектроскопияЭнергетические уровни
E
r
вращательные уровни (j)
колебательные уровни ( v)
электронные уровни (n)
8
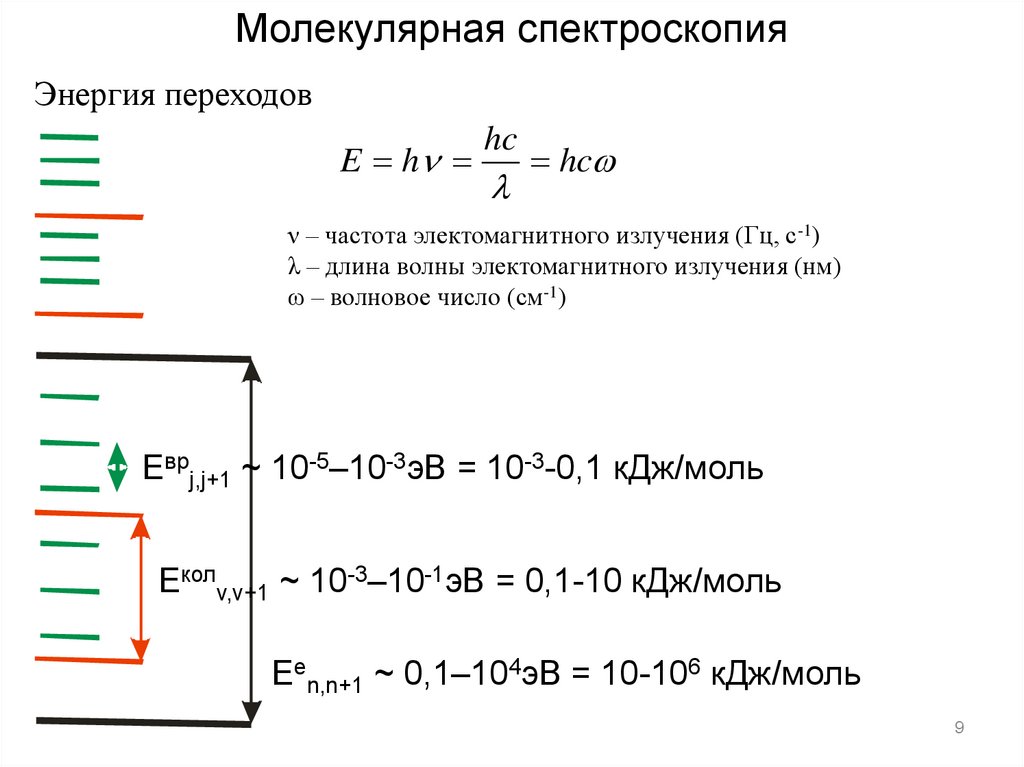
9.
Молекулярная спектроскопияЭнергия переходов
E h
hc
hc
ν – частота электомагнитного излучения (Гц, с-1)
λ – длина волны электомагнитного излучения (нм)
ω – волновое число (см-1)
Eврj,j+1 ~ 10-5–10-3эВ = 10-3-0,1 кДж/моль
Eколv,v+1 ~ 10-3–10-1эВ = 0,1-10 кДж/моль
Een,n+1 ~ 0,1–104эВ = 10-106 кДж/моль
9
10.
• Электронное движение молекулы-это движениеэлектронов, которые образуют молекулы относительно
ядра. Это движение соответствует его энергия Ее
называется электронной энергией.
• Колебательное движение молекулы-периодические
изменения взаимного расположения ядер. Энергия,
соответствующая этому движению, называется
колебательной энергией Еv.
• Вращательное движение молекулы-это периодическое
изменение положения молекулы в пространстве. Энергия
Ej, соответствующая этому движению, называется
вращательной энергией
11.
• Если при взаимодействии молекулы с квантом изменяется толькоэнергия его вращения, соответствующие спектры называются чисто
вращательными. Чистые вращающиеся спектры обычно наблюдаются
в микроволновой или дальней инфракрасной областях.
• Если при взаимодействии излучения с веществом изменяется энергия
колебаний и энергия вращения молекул газа, то спектр называется
колебательно-вращательным. Такие спектры обычно располагаются в
ближней и средней зоне ИК и представляют собой систему полос,
разделенных на отдельные линии.
• Если эффекты (линии, полосы) в спектрах вызваны перемещением
электронов между энергетическими уровнями молекул газа, то такие
спектры называются электронными, точнее электронноколебательными или электронно-колебательно-вращательными.
Электронные спектры обычно появляются в видимых и
ультрафиолетовых областях.
12.
13.
Корпускулярная природаэлектромагнитного излучения.
Для описания электромагнитного излучения как потока частиц
(фотонов, или квантов света) служит соотношение, выведенное
Эйнштейном:
ΔE=hν=hc\λ,
Классификация спектроскопических методов
1. По типу электромагнитного излучения
2. По характеру взаимодействия излучения с веществом:
спектроскопия поглощения (абсорбционная), испускания
(эмиссионная), рассеяния (комбинационного рассеяния) и
отражения (спектроскопия отражения).
3. По изучаемым объектам: на атомную и молекулярную.
4. По способу регистрации спектра: визуальные, фотографические и
фотоэлектрические.
14. Метод молекулярной спектрометрии основан на поглощении световых волн молекулами вещества.
• Свет - это электромагнитные волны с длинойволны 4*10-7 - 8*10-7 м. Электромагнитные
волны излучаются при ускоренном движении
заряженных частиц. Для того чтобы атом начал
излучать энергию, ему необходимо передать
энергию. Излучая, атом теряет полученную
энергию, и для непрерывного свечения вещества
необходим приток энергии к его атомам извне.
15.
16.
Цвета видимогоспектра
Цвет
Диапазон длин
волн, нм
Диапазон
частот, ТГц
Диапазон энергии
фотонов, эВ
Красный
625—740
480—405
1,68—1,98
Оранжевый
590—625
510—480
1,98—2,10
Жёлтый
565—590
530—510
2,10—2,19
Зелёный
500—565
600—530
2,19—2,48
Голубой
485—500
620—600
2,48—2,56
Синий
440—485
680—620
2,56—2,82
Фиолетовый
380—440
790—680
2,82—3,26
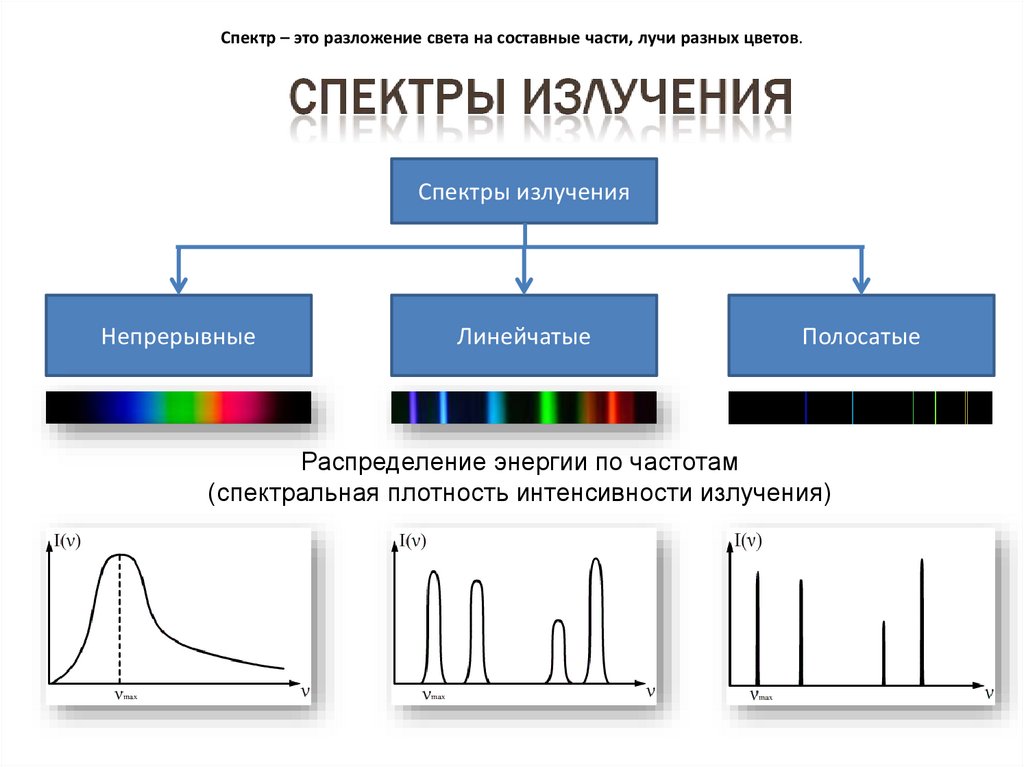
17. Спектр – это разложение света на составные части, лучи разных цветов.
Спектры излученияНепрерывные
Линейчатые
Полосатые
Распределение энергии по частотам
(спектральная плотность интенсивности излучения)
18.
• Дают тела, находящиеся в твердом,жидком состоянии, а также плотные газы.
• Чтобы получить, надо нагреть тело до
высокой температуры.
• Характер спектра зависит не только от
свойств отдельных излучающих атомов,
но и от взаимодействия атомов друг с
другом.
• В спектре представлены волны всех
длин и нет разрывов.
• Непрерывный спектр цветов можно
наблюдать на дифракционной решетке.
Хорошей демонстрацией спектра
является природное явление радуги.
19.
Линейчатые спектры играют особо важную роль, потому что ихструктура прямо связана со строением атома. Ведь эти спектры
создаются атомами, не испытывающими внешних воздействий.
Главное свойство линейчатых спектров состоит в том, что длины волн
(или частоты) линейчатого спектра какого-либо вещества зависят
только от свойств атомов этого вещества, но совершенно не зависят от
способа возбуждения свечения атомов.
Атомы любого химического элемента дают спектр, не похожий
на спектры всех других элементов: они способны излучать строгоопределенный набор длин волн.
На этом и основан спектральный анализ - метод определения
химического состава вещества по его спектру.
20.
Спектр состоит из отдельных полос, разделенных темными промежутками.Каждая полоса представляет собой совокупность большого числа очень
тесно расположенных линий.
Создаются молекулами, не связанными или слабосвязанными друг с
другом.
Для наблюдения используют свечение паров в пламени или свечение
газового разряда.
21.
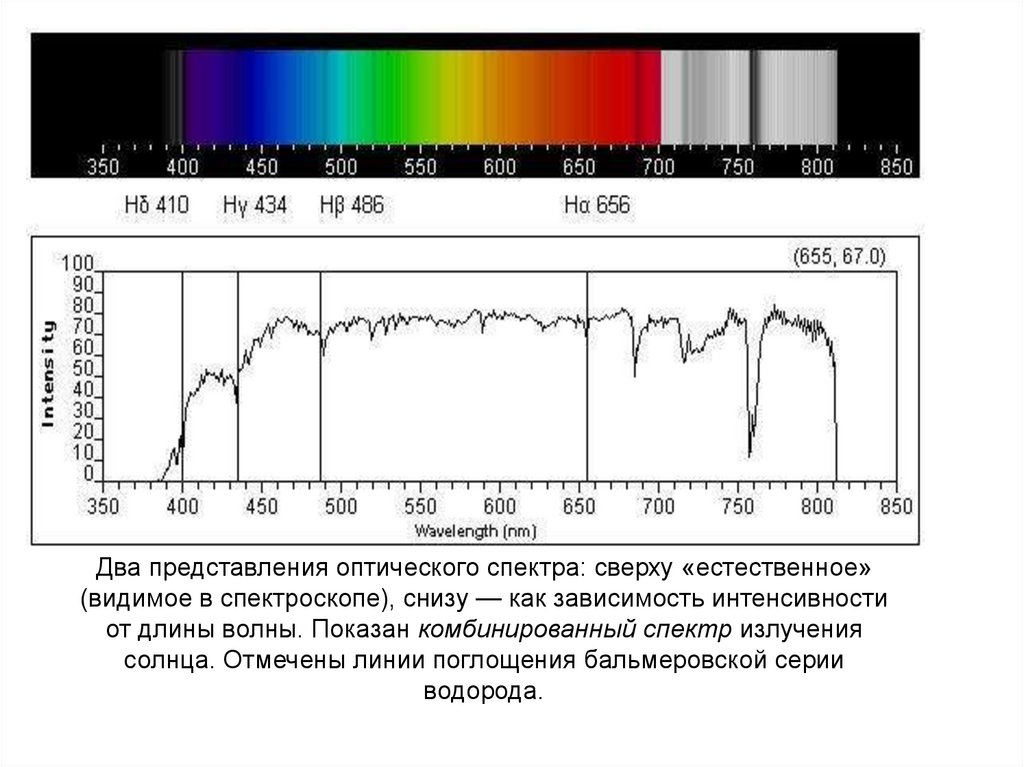
Два представления оптического спектра: сверху «естественное»(видимое в спектроскопе), снизу — как зависимость интенсивности
от длины волны. Показан комбинированный спектр излучения
солнца. Отмечены линии поглощения бальмеровской серии
водорода.
22.
• Молекулярные спектры существенноотличаются от спектров атомов, так как
движение образующих молекулу частиц
является более сложным. Наряду с
движением электронов в молекуле может
происходить периодическое изменение
относительного расположения ядер
(колебательные движения молекулы), а
также периодическое изменение ее
ориентации в пространстве как целого
(вращательное движение молекулы).
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
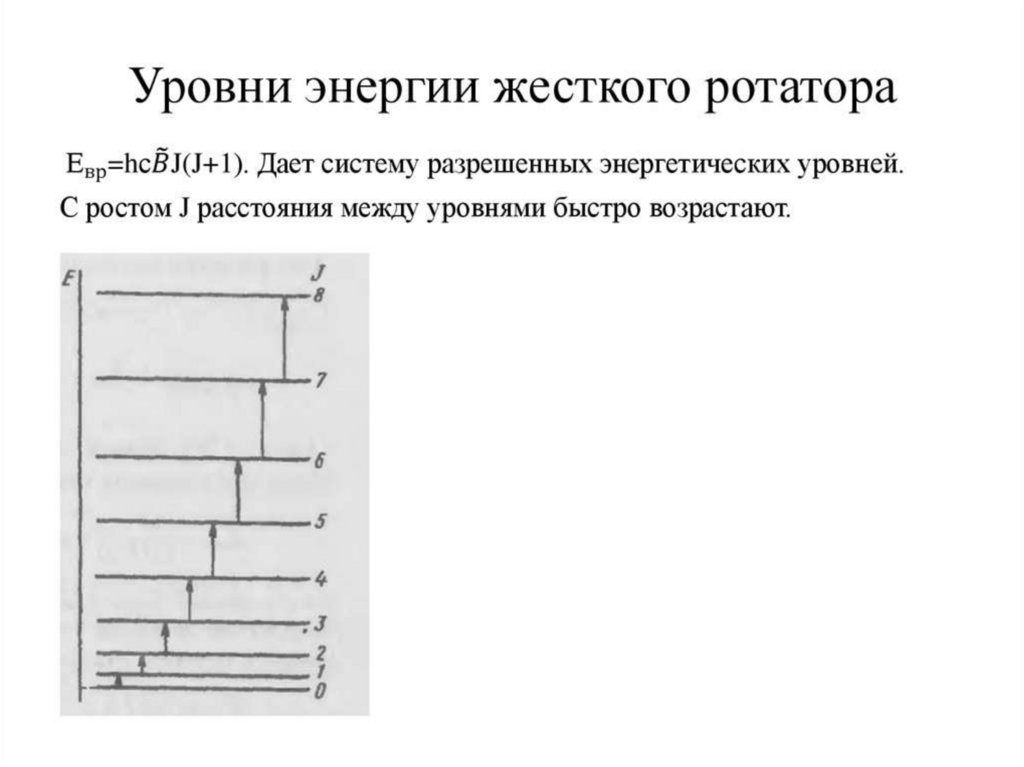
35. Вращательные спектры двух атомных молекул.
Er=h2j(j+1)/8π2J
(1)
Er=Be·j(j+1)
(2)
Be=h2/8πJ
ΔEr=Er′-Er″=h2[j′(j′+1)-j″( j″+1)]
(3)
Δj=±1 , j′- j″=1.
Отсюда уравнение (3) запишем в следующем виде:
ΔEr= h2j(j+1)/4π2J (4)
ΔEайн= hс ν
ν= ΔEайн/ hс= h (j+1)/4π2Jc
(5)
ν =B′e· (j+1) (6)
36.
B′e= h/4π2Jc-вращательная постоянная,ед.измерения м-1.
B′e=5,5981·10-44/J
J=∑miri2 (7)
J= m1r12+ m2r22 (8)
J=μ rе2 (9)
Здесь μ-приведенная масса:
μ= m1·m2/ m1+m2= а1·а2/ а1+а2· mс/12 (10)
аi-атомная массв, mс-масса атома
углерода,mс/12=1,6604·10-27кг
• Δ ν= ν2- ν1 = B′e
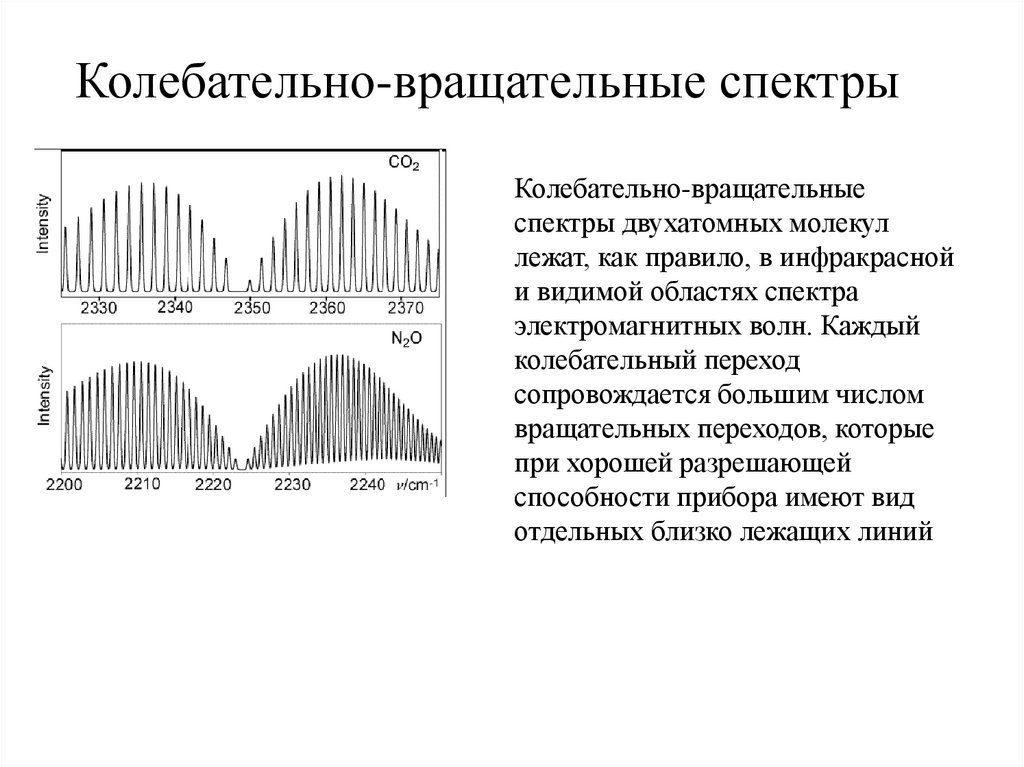
37. Колебательно-вращательные спектры
• При поглощении инфракрасного излучения происходитизменение энергии колебаний молекулы; электронное
состояние
остается
неизменным.
Переходы
между
колебательными
уровнями
всегда
сопровождаются
одновременными изменениями вращательной энергии. В
результате возникают колебательно-вращательные спектры. Эти
спектры в инфракрасной области имеют молекулы симметрии
C∞v, состоящие из неодинаковых атомов и имеющие
дипольный момент. Изменения вращательной энергии, как
правило, малы по сравнению с изменениями колебательной
энергии. Поэтому в спектрах получаются полосы (линии),
соответствующие определенному колебательному переходу,
тонкая структура которых обусловлена вращательными
переходами – колебательно-вращательные полосы.
38. Колебательно-вращательные спектры
Колебательно-вращательныеспектры двухатомных молекул
лежат, как правило, в инфракрасной
и видимой областях спектра
электромагнитных волн. Каждый
колебательный переход
сопровождается большим числом
вращательных переходов, которые
при хорошей разрешающей
способности прибора имеют вид
отдельных близко лежащих линий
39. МОДЕЛЬ ЖЕСТКИЙ РОТАТОР – ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
• Если использовать приближения о независимости различных видовдвижения молекулы (поступательного, вращательного, колебательного
и электронного); тогда полная энергия молекулы равна сумме энергий
этих видов движения. Энергия колебательно-вращательных состояний
молекулы Evr (в см–1 – обратных сантиметрах)1 в приближении
«жесткий ротатор – гармонический осциллятор» является суммой
колебательной
• Ev = ωe(v + ½) и вращательной Er = BeJ(J + 1)
• энергий и определяется выражением
• Evr = ωe(v + ½) + BeJ(J + 1) (1)
• где Be, см–1 – вращательная постоянная, J = 1, 2, 3 … вращательное
квантовое число, ωe, см–1– гармоническая колебательная v = 0, 1, 2, 3
… - колебательное квантовое число. Индекс «е» обозначает, что
соответствующие
величины
рассчитаны
для
равновесной
конфигурации молекулы.
Для того, чтобы выразить энергию в Джоулях, надо энергию в см–1 умножить на произведение
постоянной Планка h = 6,62607 × 10–34 Дж с и скорости света с = 2,99792 × 1010 см/с,
Evr (Дж) = Evr (см–1 )×h(Дж·с)×с(см/с).
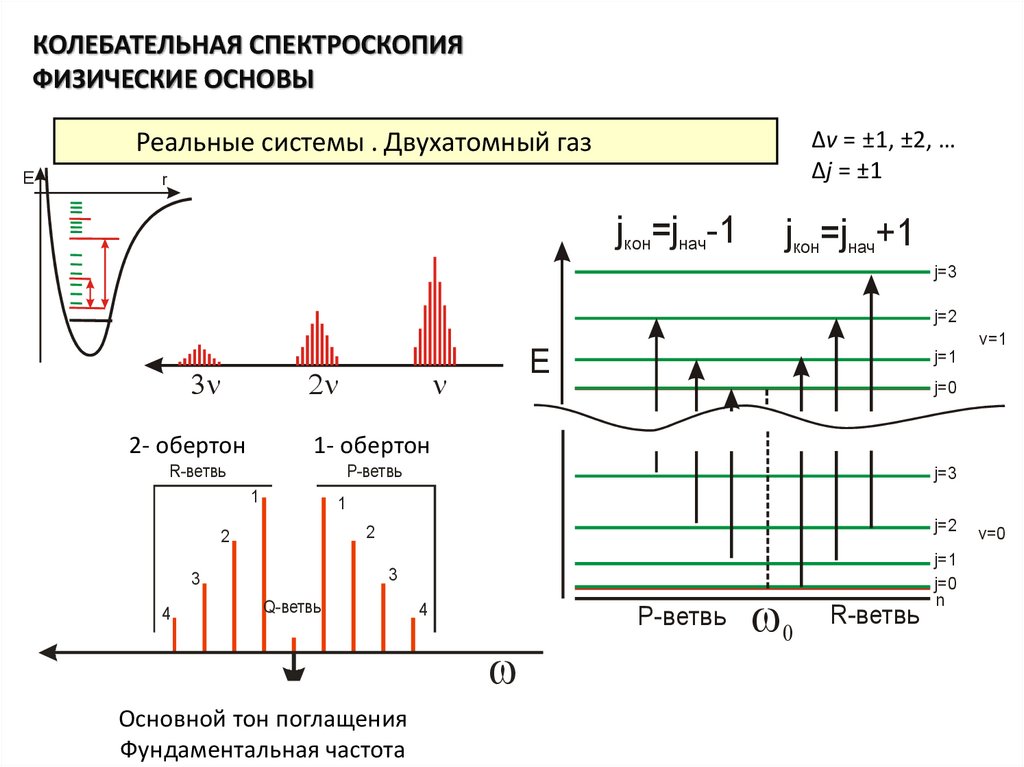
40. МОДЕЛЬ ЖЕСТКИЙ РОТАТОР – ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
• Разрешенные переходы между уровнями энергии молекулыопределяются правилами отбора. Для колебательно-вращательных
спектров двухатомных молекул, правила отбора следующие: для
вращательного квантового числа ΔJ = ±1, для колебательного
квантового числа Δv = ±1 (в гармоническом приближении). С учетом
ангармоничности колебаний, разрешены также переходы Δv = ±2, ±3
… . И действительно, линии таких переходов наблюдаются в
эксперименте (так как колебания молекул на самом деле
ангармонические). Однако их интенсивность намного меньше, чем
линии перехода Δv = ±1. Переходы с ΔJ = +1 образуют R-ветвь
колебательно-вращательной полосы, ΔJ = –1 образуют P-ветвь.
• Переходы между нулевым v’’ = 0 и первым возбужденным v’ = 1
колебательными уровнями называются основными, или
фундаментальными. Здесь и далее, для любых переходов, нижний
уровень обозначается двумя штрихами ‘’, верхний уровень – одним
штрихом ‘.
41.
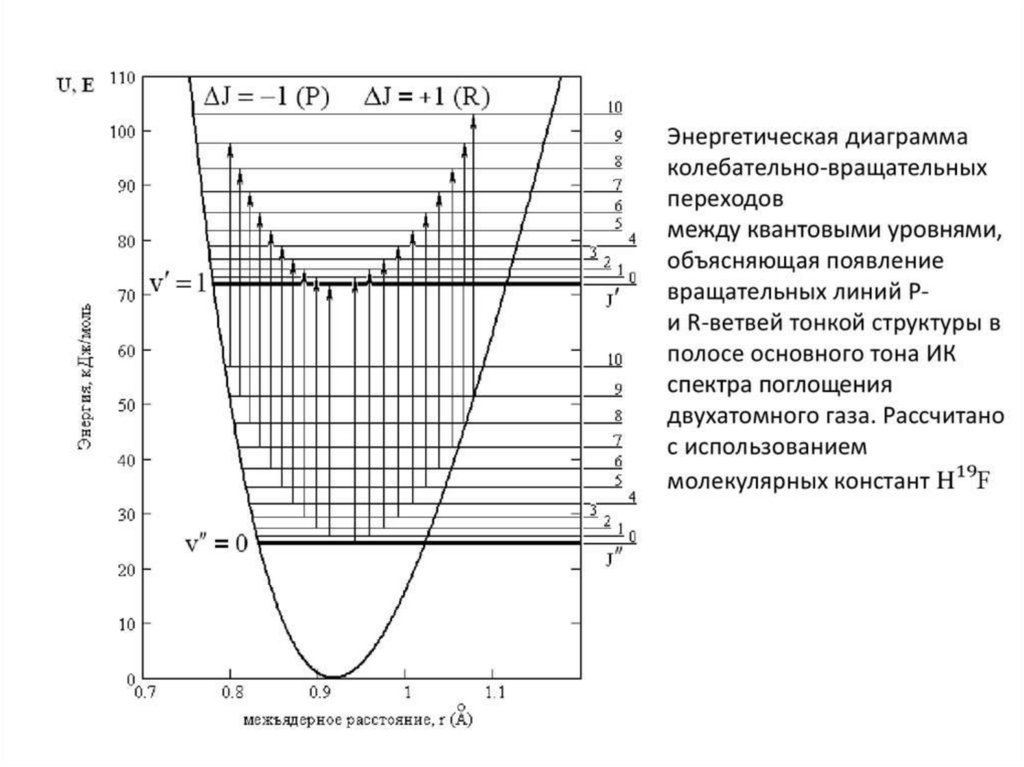
КОЛЕБАТЕЛЬНАЯ СПЕКТРОСКОПИЯФИЗИЧЕСКИЕ ОСНОВЫ
∆v = ±1, ±2, …
∆j = ±1
Реальные системы . Двухатомный газ
E
r
jкон=jнач-1
jкон=jнач+1
j=3
j=2
v=1
E
j=1
j=0
2- обертон
1- обертон
R-ветвь
P-ветвь
j=3
2
j=2
1
1
2
3
3
4
Q-ветвь
4
P-ветвь
Основной тон поглащения
Фундаментальная частота
R-ветвь
j=1
j=0
n
v=0
42.
• Согласно выражению (1), энергии нижнего E’’ и верхнего E’ уровнейравны E’’(v’’ = 0) = ωe·1/2 + BeJ’’(J’’ + 1),
• E’(v’ = 1) = ωe·3/2 + BeJ’(J’ + 1).
• Волновое число линий в полосе фундаментального перехода
• ν = E’(v’= 1) – E’’(v’’= 0) = ωe + Be[J’ (J’ + 1) – J’’ (J’’ + 1)]. (2)
• Линия с волновым числом ωe соответствует чисто колебательному
переходу, который получился бы при J’ = J’’ = 0 («нулевая линия»). В
силу невозможности переходов J’’ = 0 ↔ J’ = 0, нулевая линия не
может наблюдаться, и её положение определяют расчетом.
• Исходя из формулы (2), выпишем выражения волновых чисел линий в
R и P-ветвях фундаментальной полосы.
• R-ветвь (ΔJ = J’ – J’’ = 1): ν R =ω е (1-2х е )+2Be(j"+1)(3)
• P-ветвь (ΔJ = J’ – J’’ = –1): ν Р =ω е (1-2х е )-2Bej". (4)
• Оба выражения (3) и (4) можно записать в виде одной формулы, если
обозначить для R-ветви m = J’ = 1, 2, 3 …, для P-ветви m = –J’’ = –1, –
2, –3 … :
• ν = ωe + 2Bem. (5)
• Полученная формула (5) используется для определения молекулярных
постоянных ωe и Be двухатомной молекулы, исходя из её
колебательно-вращательного спектра.
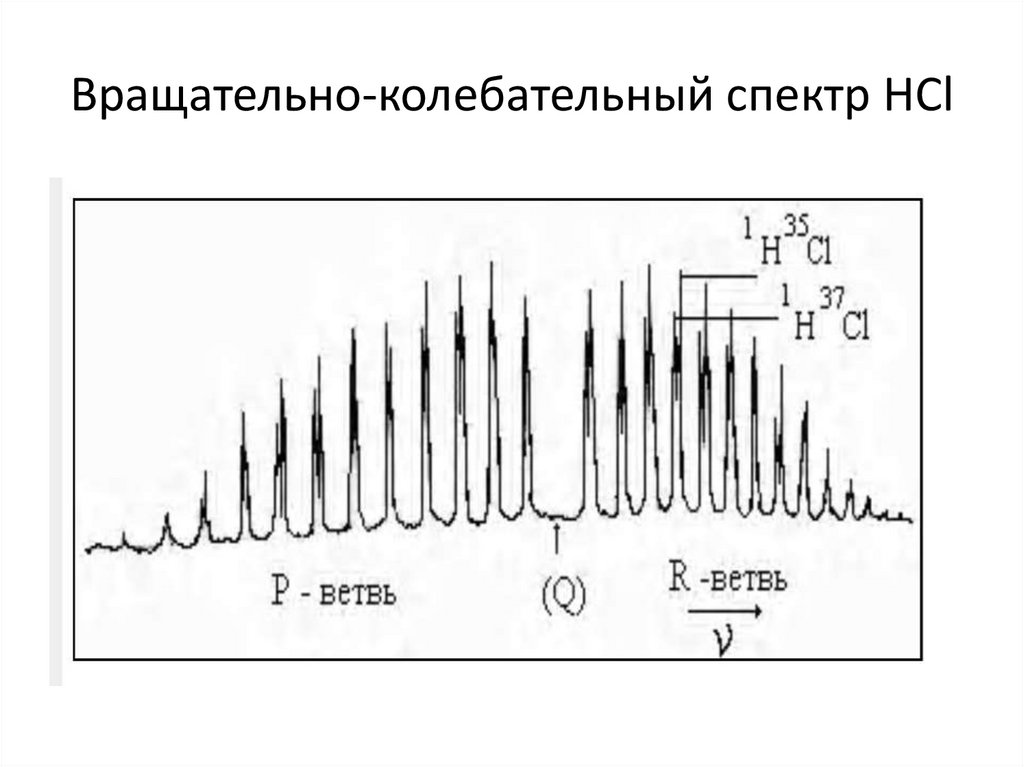
43. Вращательно-колебательный спектр НCl
44.
• Отсюда видно, что спектральная линия,соответствующая основной частоте
ω=ω е (1-2х е ), в спектре не проявляется;
между R- и Р- ветвями возникает
«нулевой промежуток» в 4Ве (рис.8), а
разность между двумя соседними линиями
для модели жесткой сферы в R- и Рветвях, равна 2 Be, т.е
• ∆ ω R,Р =2Ве=h/4π2Iс. (5)
45. МОДЕЛЬ ВРАЩАЮЩИЙСЯ АНГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
• Оказывается, что модель «жесткий ротатор – гармоническийосциллятор» не может описать все наблюдаемые в
эксперименте
особенности
колебательно-вращательных
спектров двухатомных молекул. Поэтому она нуждается в
уточнении. Для большинства практических задач, достаточно
дополнительно учесть два фактора: 1) ангармоничность
колебаний (т.е. на самом деле колебания молекул не являются
гармоническими);
• 2) зависимость вращательной постоянной от колебательного
состояния. При этом энергия ангармонических колебаний с
хорошей точностью определяется выражением
• Ev = ωe(v + ½) + ωexe(v + ½)2 (6), где ωexe – ангармоническая
поправка, xe – первая постоянная ангармоничности (xe << 1).
46. МОДЕЛЬ ВРАЩАЮЩИЙСЯ АНГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
• При выводе уравнений (3) и (4) было принято, что В'=В".Однако при переходе с v=0 на v=1 амплитуда колебаний
увеличивается. Из-за ангармоничности колебаний равновесное
расстояние и момент инерции молекулы зависят от
колебательного квантового числа. Следовательно, вращательная
характеристика молекулы В не является постоянной
• (В' ≠ В"). Это ведет к увеличению момента инерции и,
следовательно, к уменьшению величины В. Для небольших
значений v зависимость В=f(v) можно представить линейным
уравнением
• Вv=Вe-α(v+1/2) (7) выражающая зависимость вращательной
постоянной от колебательного квантового числа v .
• где
αe
–
постоянная
колебательно-вращательного
взаимодействия.
47. МОДЕЛЬ ВРАЩАЮЩИЙСЯ АНГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
• В рамках уточненной модели, которую можно назвать «вращающийсяангармонический осциллятор», энергия колебательно-вращательных
состояний двухатомной молекулы определяется выражением
• Evr = ωe(v + ½) – ωexe(v + ½)2 + [Be – αe(v + ½)] J (J + 1). (8)
• уравнения (3) (4) можно записать:
• ω R =ω е -2 ω е х е +2Be(j+1)-1,5α (j+1) (j+2) (8)
• ω p =ω е -2 ω е х е -2Bej-1,5α (j-1) (j+2) j (9)
• Опыт показывает, что при увеличении колебательного числа линии в
R- ветви сближаются, а в P-ветви – удаляются








































 Физика
Физика








