Распределения случайных величин. Статистические функции в Python: scipy.stats

1.

Распределения случайных величин.
Статистические функции в Python:
scipy.stats

2.

Распределение Бернулли
• Пол родившегося ребёнка

3.

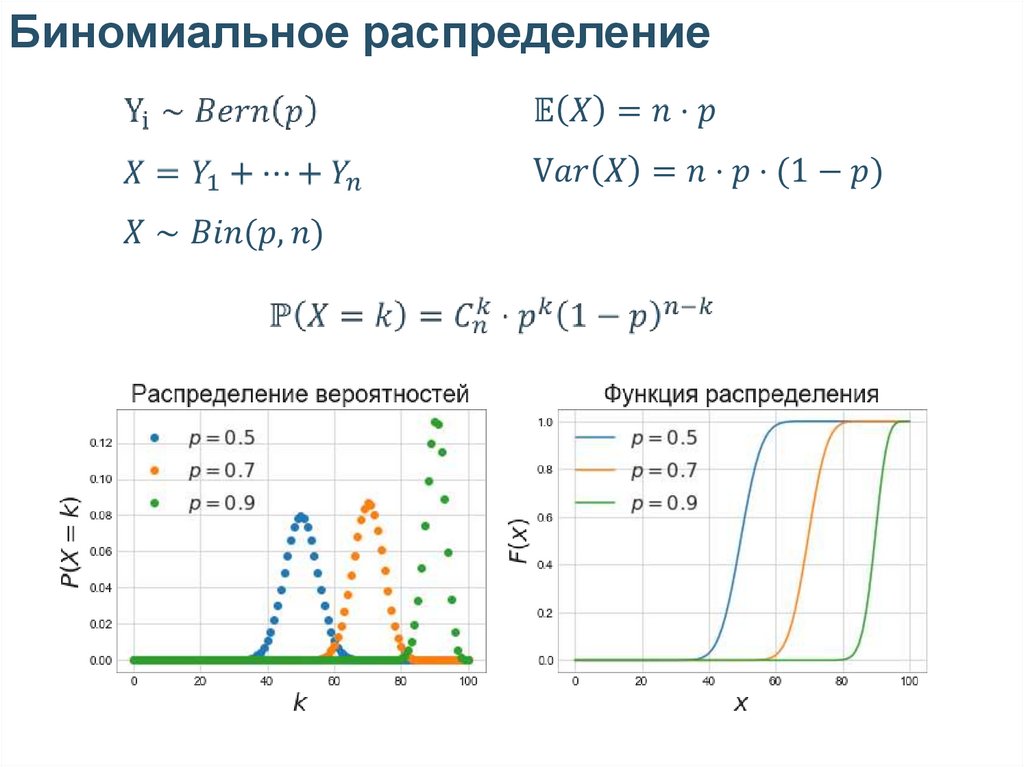
Биномиальное распределение
• Число попаданий
в баскетбольную корзину
Futurama s03 e14. Автор Мэтт Грейнинг. FOX Network.
Futurama s03 e14

4.

Биномиальное распределение

5.

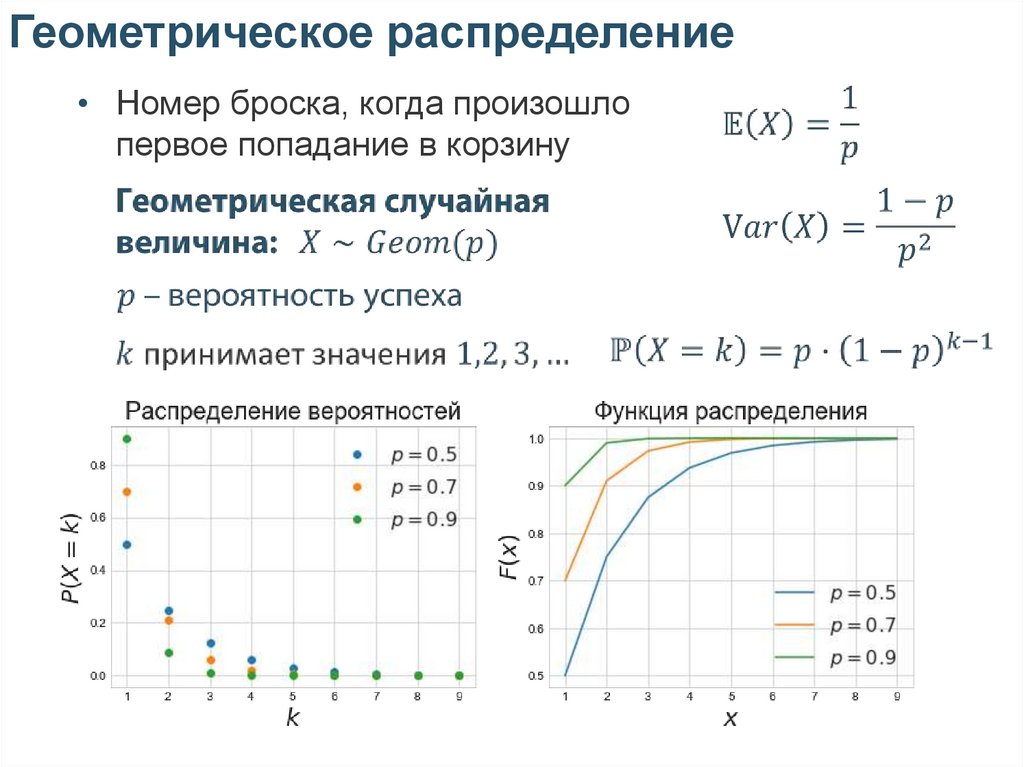
Геометрическое распределение
• Номер броска, когда произошло
первое попадание в корзину

6.

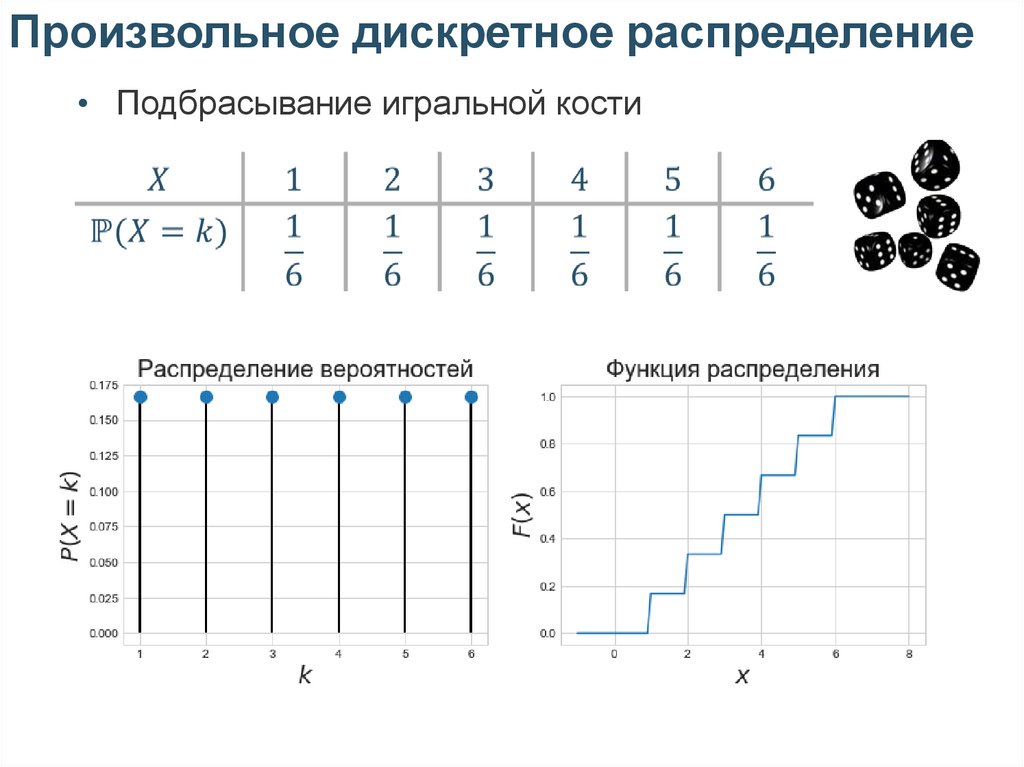
Произвольное дискретное распределение
• Подбрасывание игральной кости

7.

Счётчики
• Число людей в очереди
• Число лайков под фото
• Число автобусов, проехавших за час мимо остановки

8.

Счётчики
• Число людей в очереди
• Число лайков под фото
• Число автобусов, проехавших за час мимо остановки
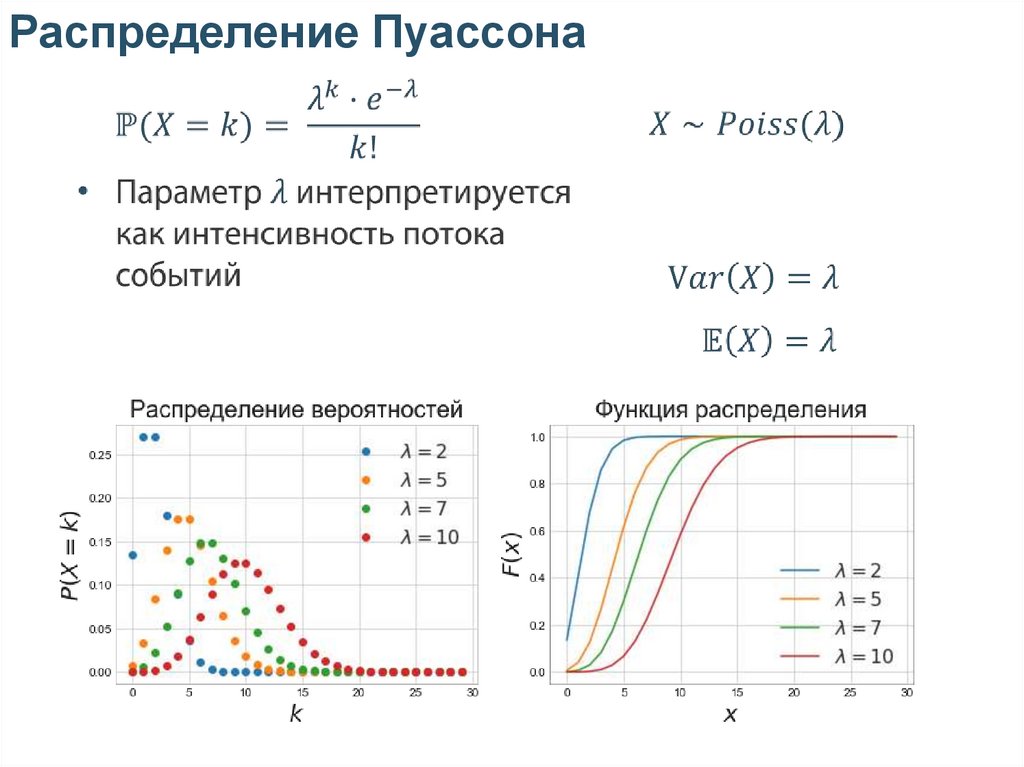
Распределение Пуассона
хорошо описывает
счётчики
w-dog.ru / vk.com

9.

Распределение Пуассона

10.

Время до …
• Время ожидания трамвая
• Время до прихода нового человека в очередь
• Время до поломки механизма
• Интервалы времени
между событиями
• Модели времени жизни
Wikipedia.org, Картина Сальвадора Дали «Постоянство памяти»

11.

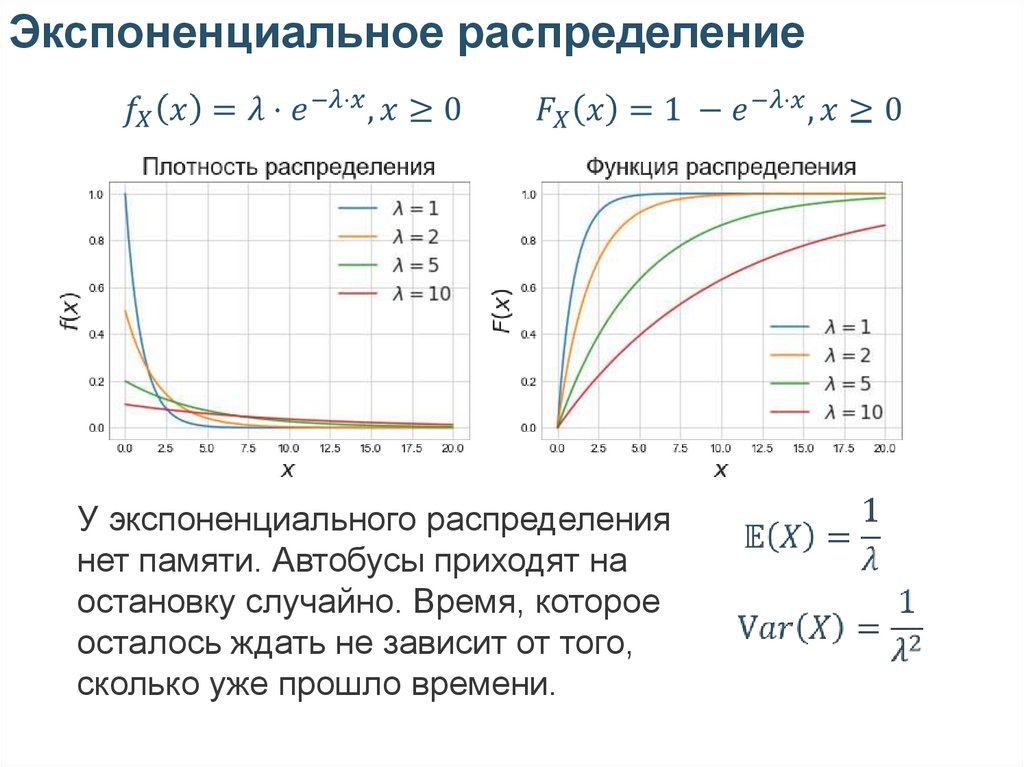
Экспоненциальное распределение
У экспоненциального распределения
нет памяти. Автобусы приходят на
остановку случайно. Время, которое
осталось ждать не зависит от того,
сколько уже прошло времени.

12.

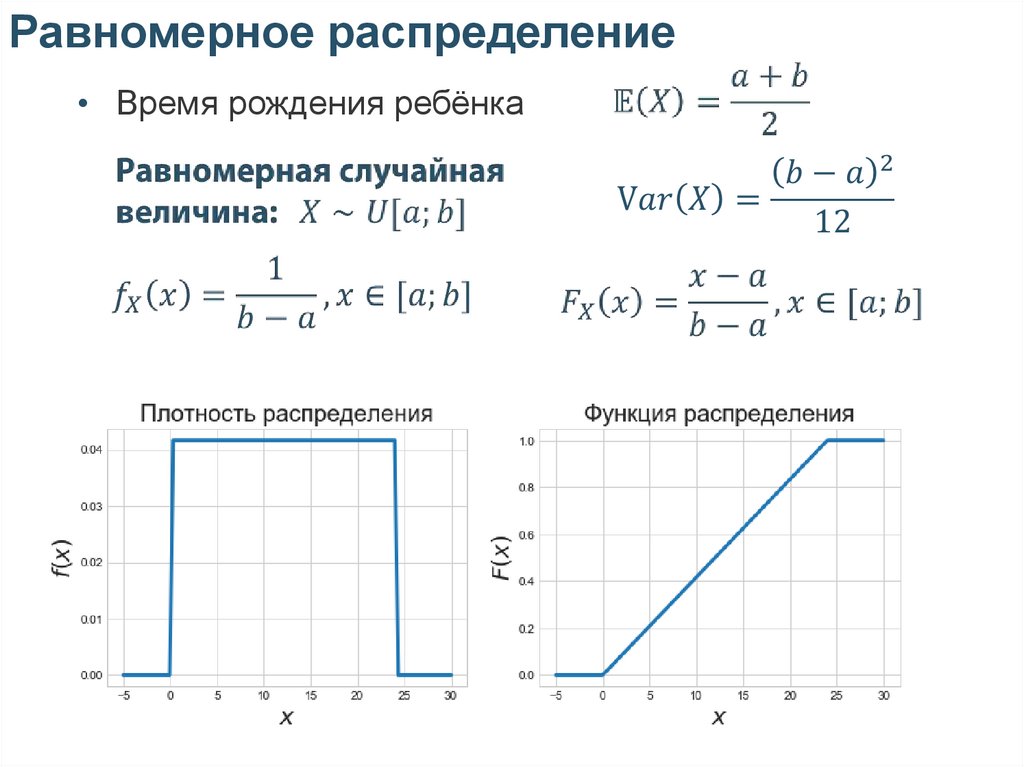
Равномерное распределение
• Время рождения ребёнка

13.

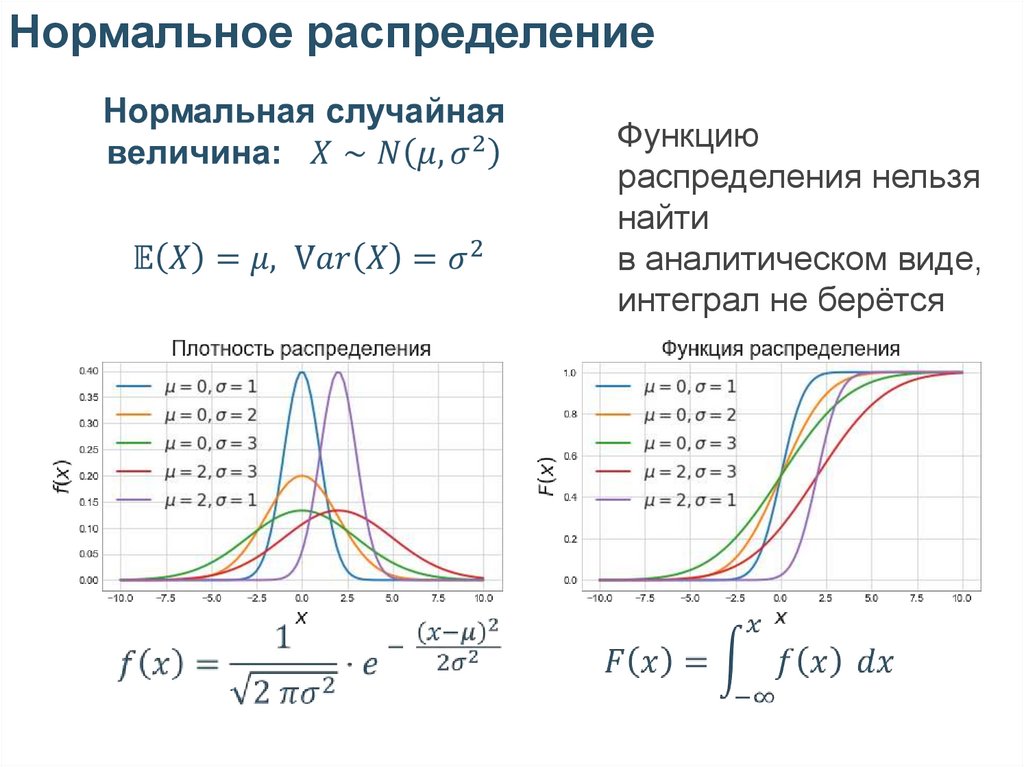
Нормальное распределение
• В статистике часто встречается нормальное
распределение
• Оно используется для проверки гипотез
и для того, чтобы понимать насколько точными
у нас получаются прогнозы и оценки
• Его обычно используют, когда у нас есть
в распоряжении большая выборка, это разрешает
делать Центральная Предельная Теорема
(о ней поговорим на будущих неделях)
• Давайте познакомиться с нормальным
распределением поближе

14.

Нормальное распределение
Функцию
распределения нельзя
найти
в аналитическом виде,
интеграл не берётся

15.

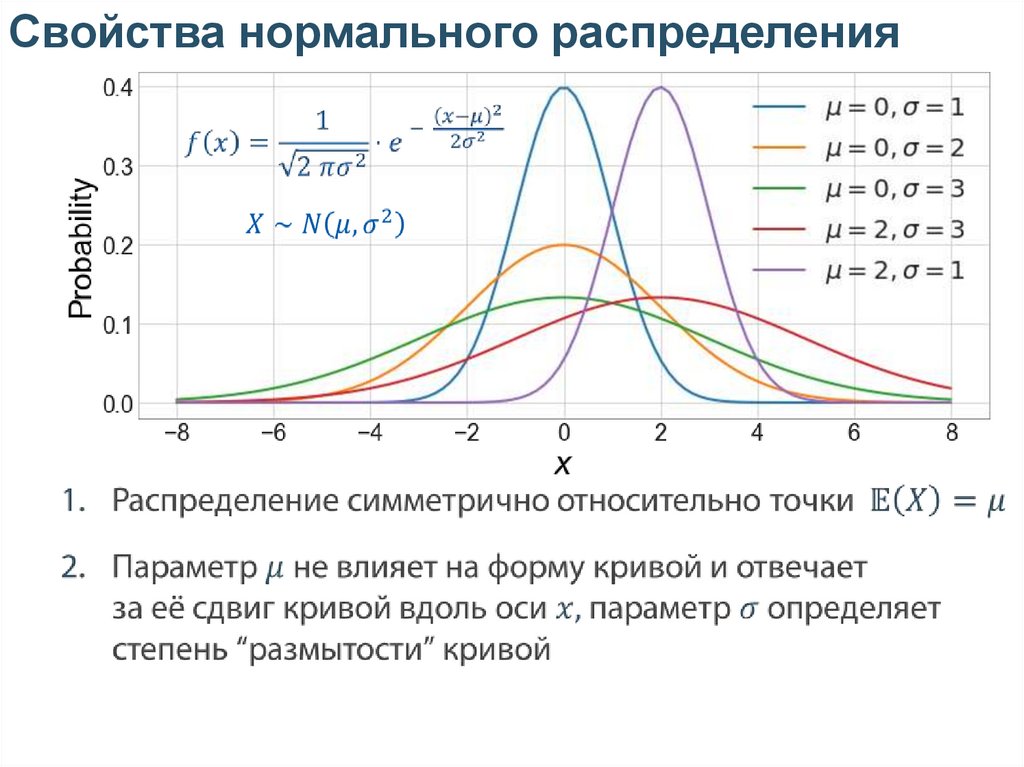
Свойства нормального распределения

16.

Свойства нормального распределения
Нормальная случайная величина устойчива
к суммированию и линейным преобразованиям

17.

Центрирование и нормирование
центрирование
нормирование

18.

Стандартное нормальное распределение

19.

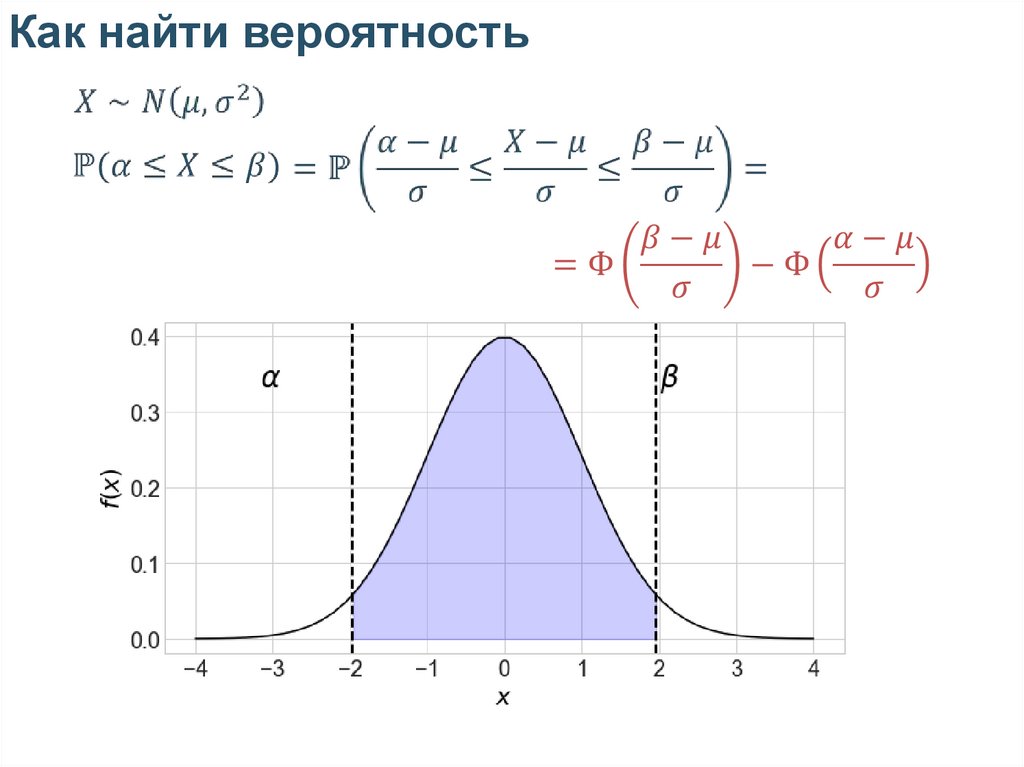
Как найти вероятность

20.

Как найти вероятность

21.

Правила сигм
Правило
сигмы:

22.

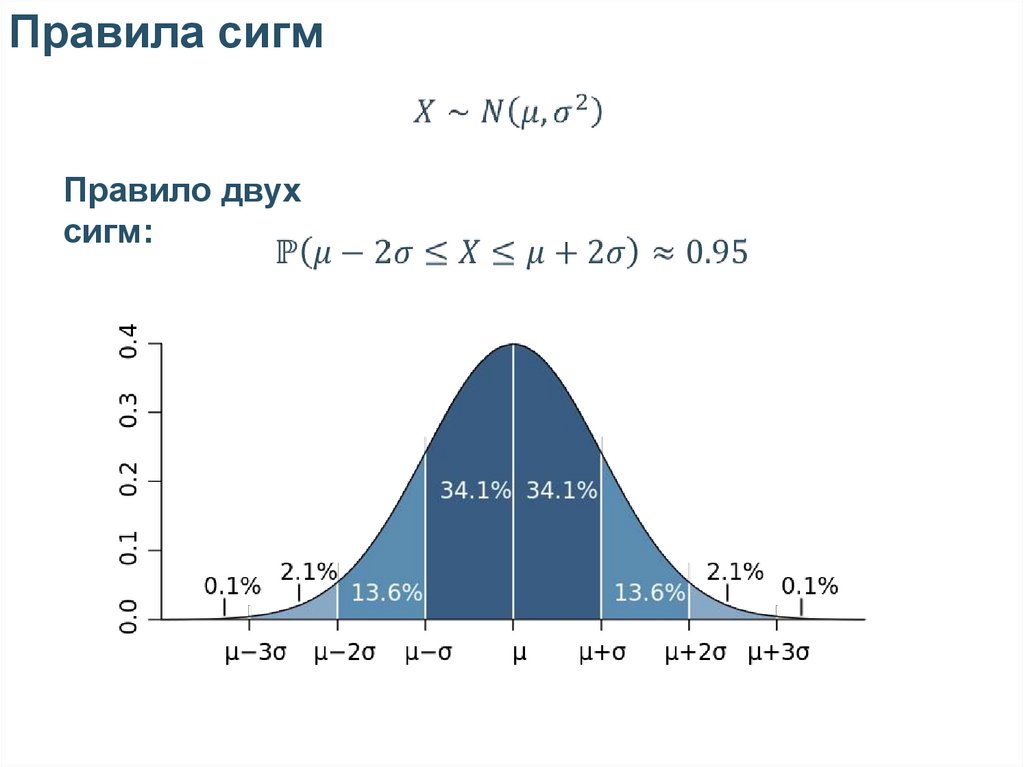
Правила сигм
Правило двух
сигм:

23.

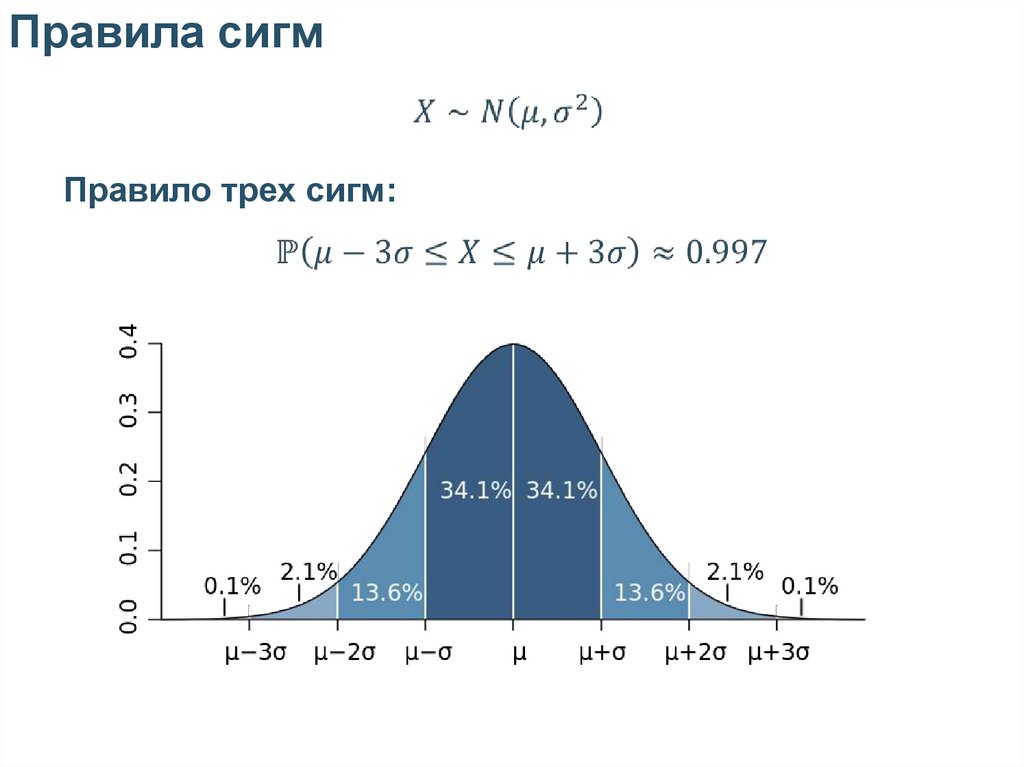
Правила сигм
Правило трех сигм:

24.

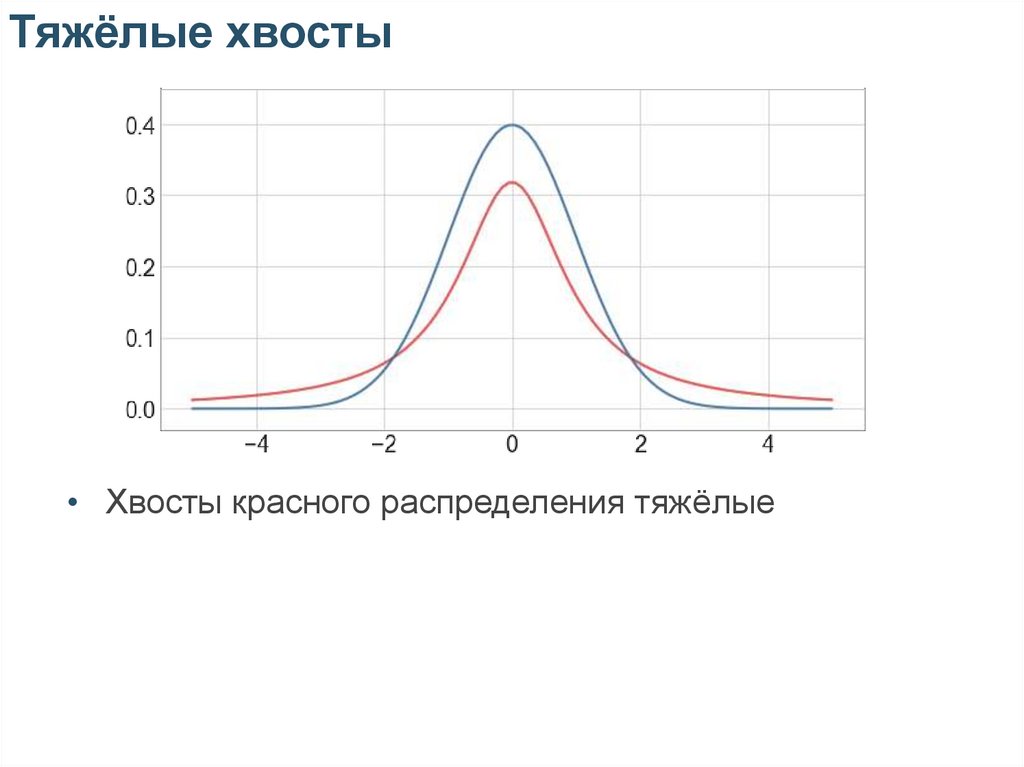
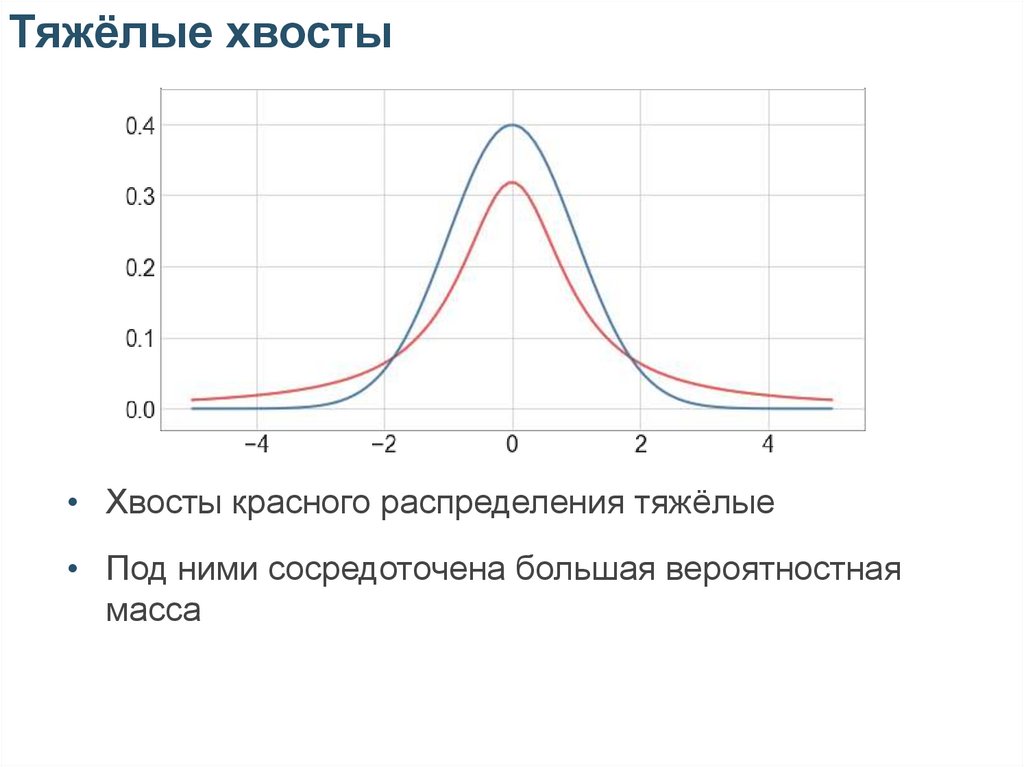
Тяжёлые хвосты
• Хвосты красного распределения тяжёлые

25.

Тяжёлые хвосты
• Хвосты красного распределения тяжёлые
• Под ними сосредоточена большая вероятностная
масса

26.

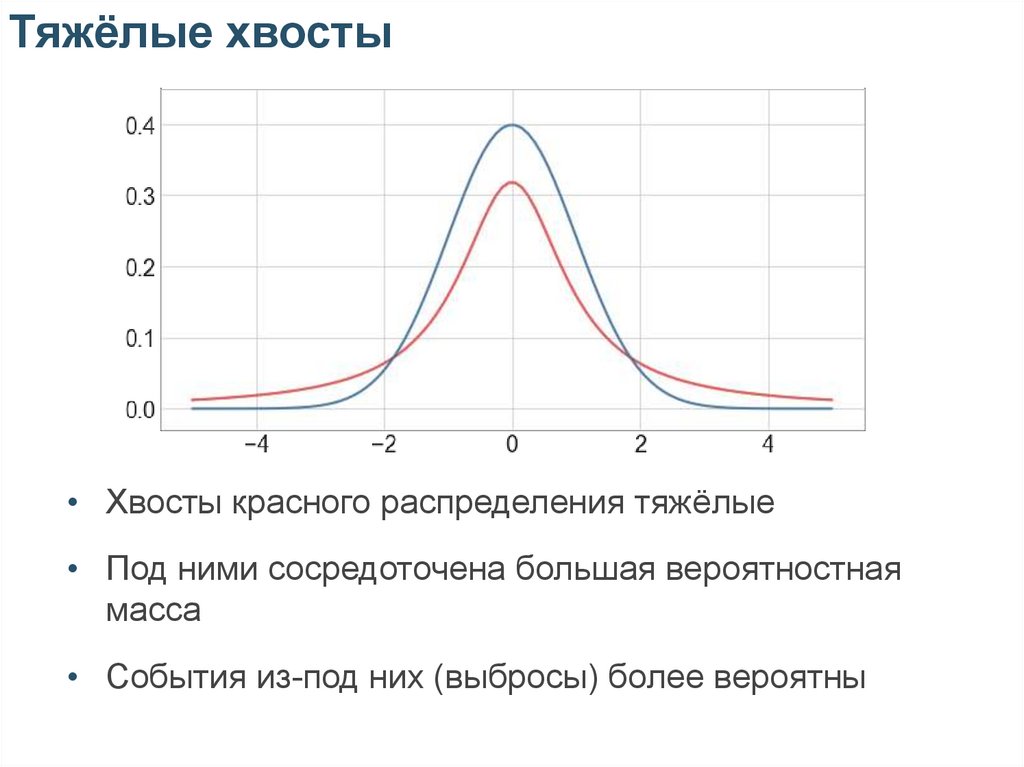
Тяжёлые хвосты
• Хвосты красного распределения тяжёлые
• Под ними сосредоточена большая вероятностная
масса
• События из-под них (выбросы) более вероятны

27.

Эксцесс и куртосис
Куртосис
Коэффициент эксцесса можно вычислить с помощью
метода kurtosis() SciPy.

28.

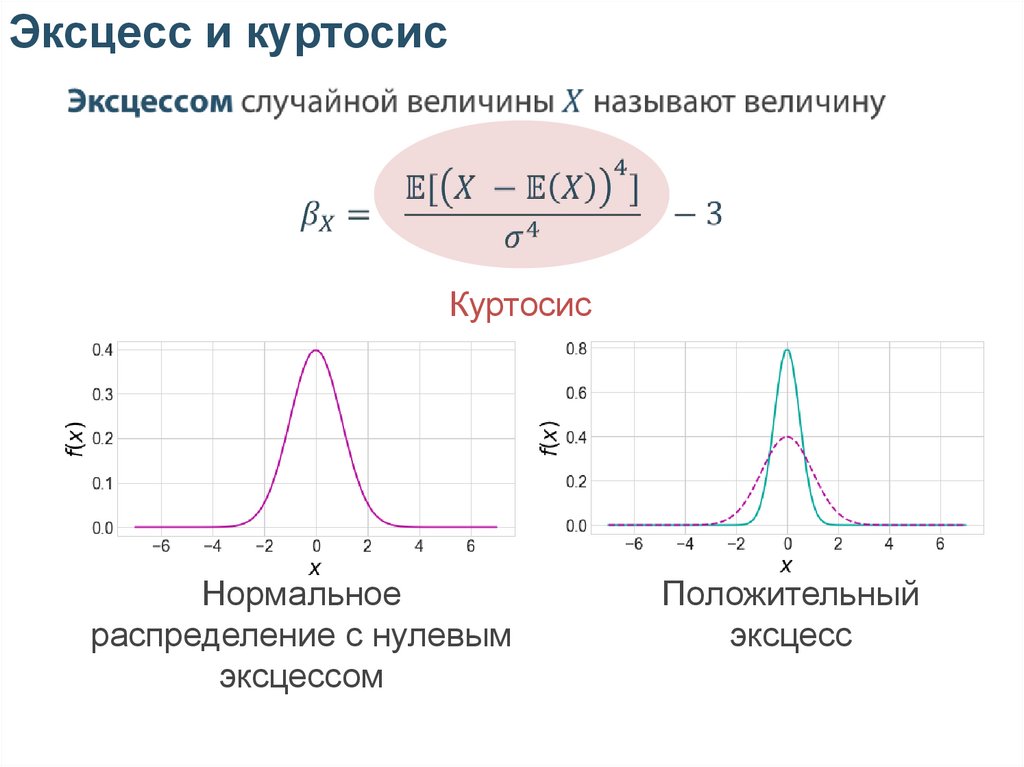
Эксцесс и куртосис
Куртосис
Нормальное
распределение с нулевым
эксцессом
Положительный
эксцесс

29.

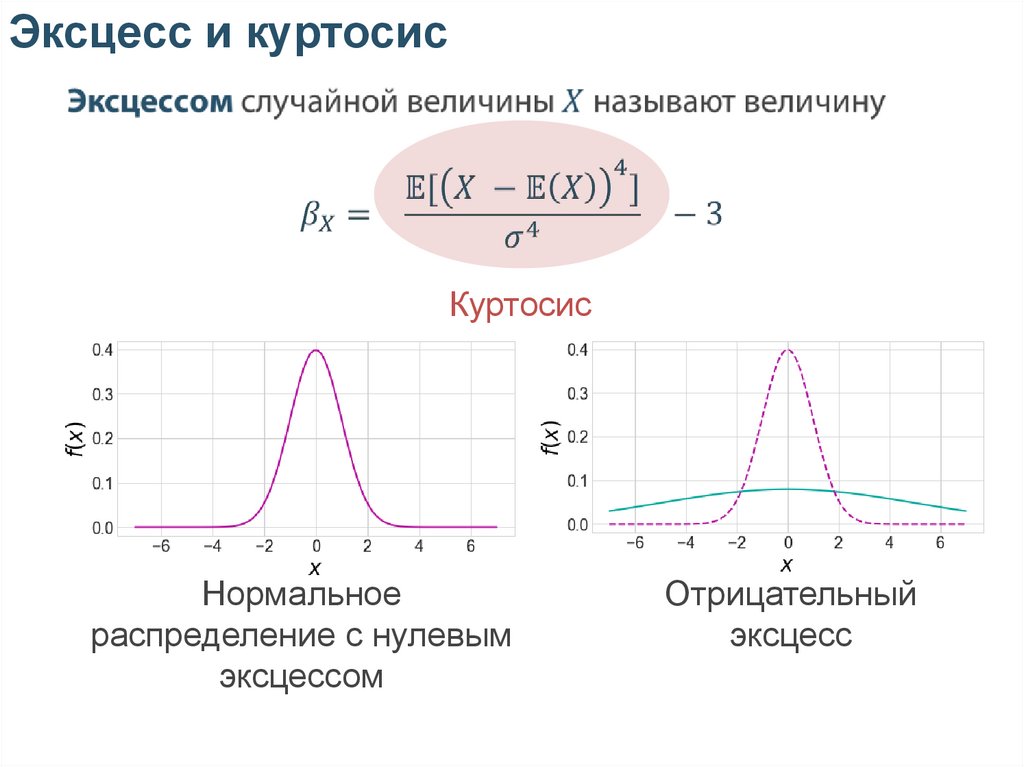
Эксцесс и куртосис
Куртосис
Нормальное
распределение с нулевым
эксцессом
Отрицательный
эксцесс

30.

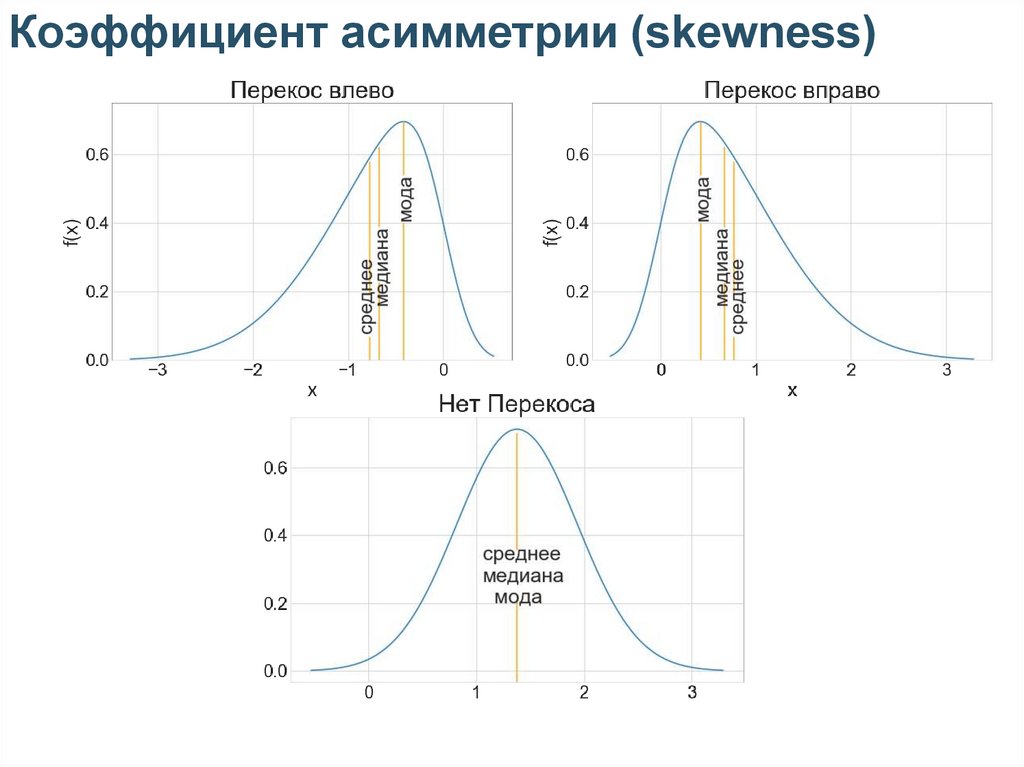
Коэффициент асимметрии (skewness)

31.

Коэффициент асимметрии (skewness)

32.

Эксцесс и асимметрия
• Эксцесс оказывается полезным при поиске тяжёлых
хвостов
• Большое значение эксцесса сигнализирует о наличии
тяжёлых хвостов и выбросов в данных
• Коэффициент асимметрии характеризует перекос
в распределении
• Если у распределения сильный перекос,
с применением стандартных статистических методов
возникают сложности

33.

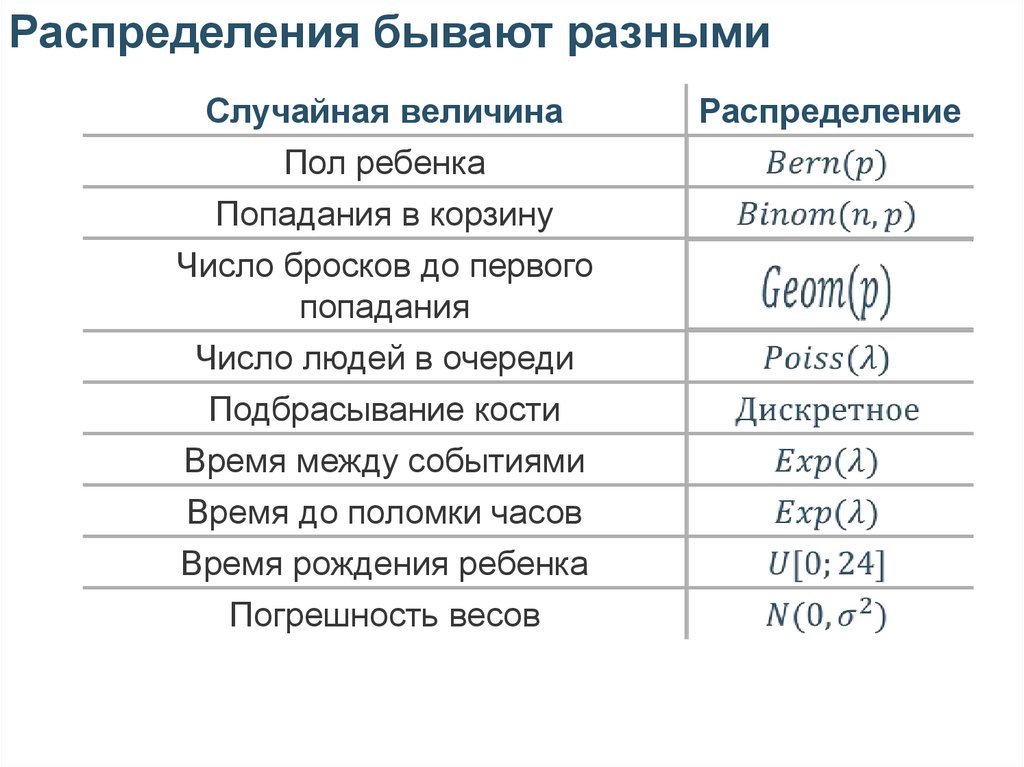
Распределения бывают разными
Случайная величина
Пол ребенка
Попадания в корзину
Число бросков до первого
попадания
Число людей в очереди
Подбрасывание кости
Время между событиями
Время до поломки часов
Время рождения ребенка
Погрешность весов
Распределение

34. Резюме

• Моделировать внутренности сундука можно с
помощью различных законов распределения
• Наиболее подходящий закон выбирается с помощью
здравого смысла
Мы перечислили лишь один из вариантов
моделировать незнание с помощью
случайной величины. Эти распределения не
истина
в последней инстанции
• Все предпосылки, связанные с выбранным законом,
должны проверяться по данным, в будущем мы
научимся это делать

35.

Распределения,
связанные с нормальным

36.

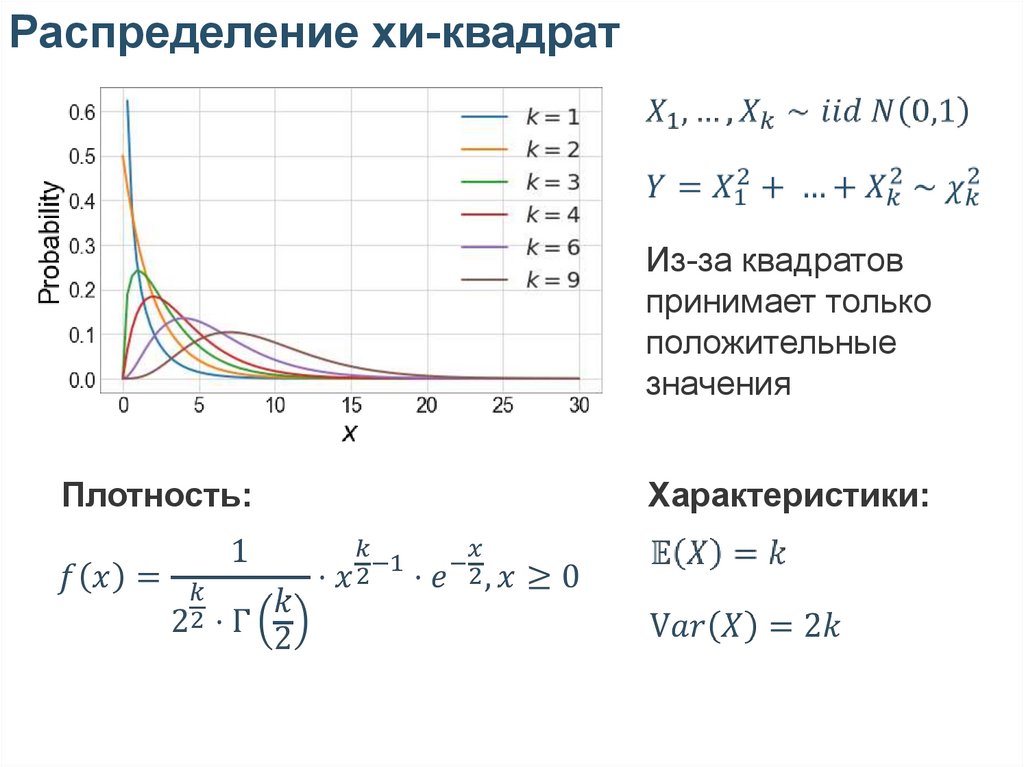
Распределение хи-квадрат
Когда возникает
на практике:

37.

Распределение хи-квадрат
Когда возникает
на практике:

38.

Распределение хи-квадрат
Из-за квадратов
принимает только
положительные
значения
Плотность:
Характеристики:

39.

Степени свободы
Число степеней свободы – количество элементов
варьирования, которые могут принимать произвольные
значения, не изменяющие заданных характеристик.

40.

Степени свободы
Число степеней свободы – количество элементов
варьирования, которые могут принимать произвольные
значения, не изменяющие заданных характеристик.

41.

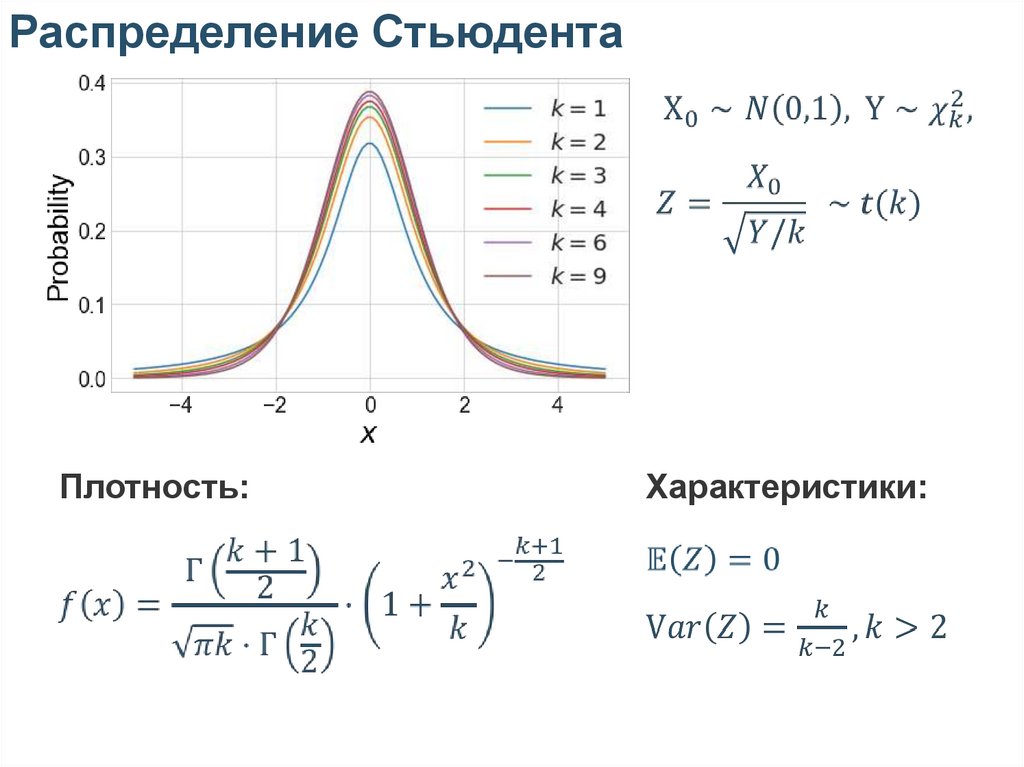
Распределение Стьюдента
Когда возникает на практике:

42.

Распределение Стьюдента
Плотность:
Характеристики:

43.

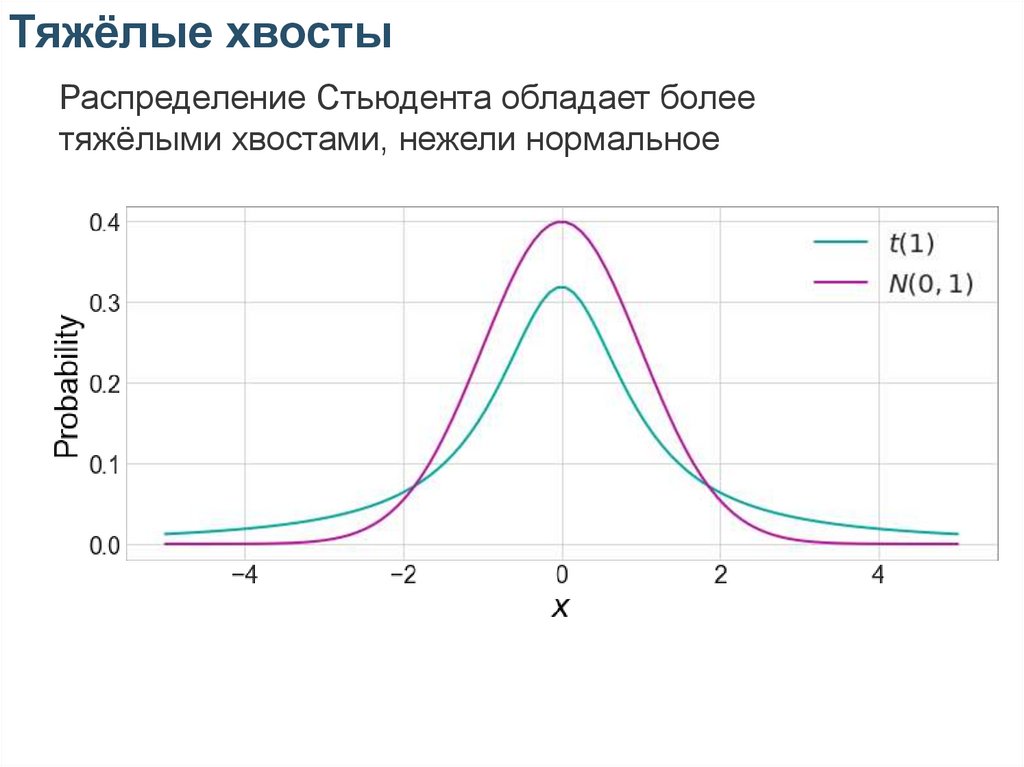
Тяжёлые хвосты
Распределение Стьюдента обладает более
тяжёлыми хвостами, нежели нормальное

44.

Распределение Фишера
Когда возникает на практике:
Встречается при сравнении дисперсий.
Чтобы сравнить их между собой, одну
дисперсию делят на вторую.

45.

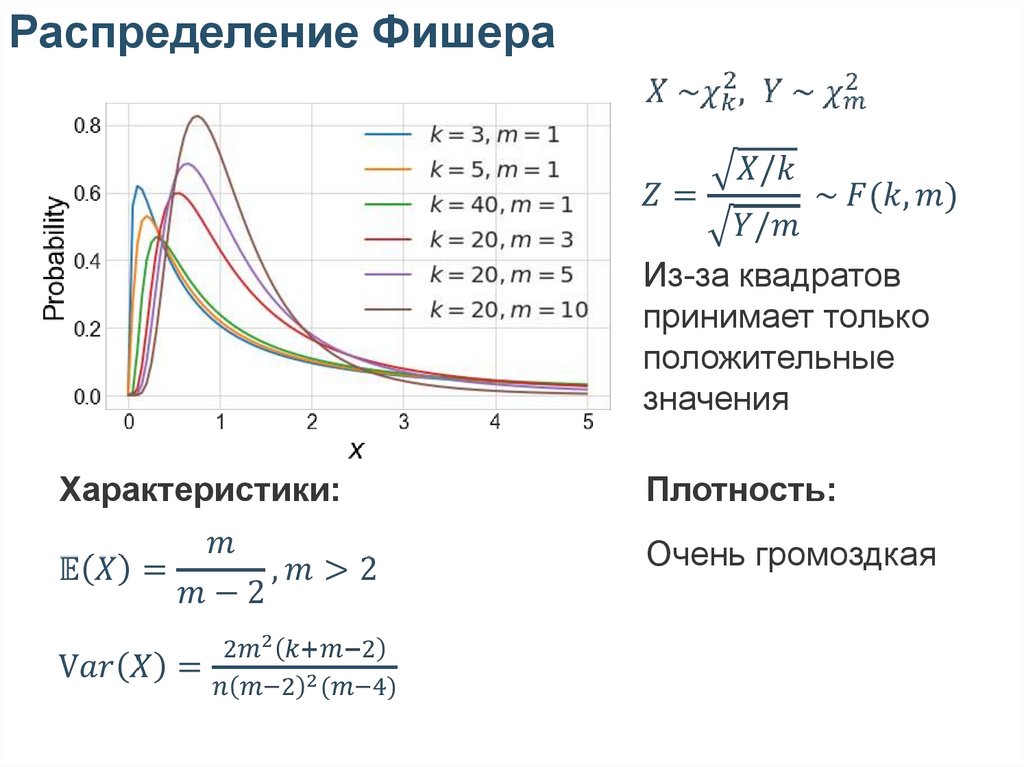
Распределение Фишера
Из-за квадратов
принимает только
положительные
значения
Характеристики:
Плотность:
Очень громоздкая

46.

Резюме
• Распределения хи-квадрат, Стьюдента, Фишера часто
встречаются на практике при анализе нормально
распределённых выборок
• В будущем мы часто будем обращаться к ним за
помощью