Похожие презентации:
Числовые характеристики случайных величин. (Тема 5)
1.
5. Числовые характеристикислучайных величин
параметр распределения
оценка параметра
меры положения (характеристики центра)
меры рассеяния (разброса, изменчивости)
характеристики формы
среднее центр группирования
математическое ожидание
2.
взвешенное среднеемода
медиана
унимодальное и бимодальное
распределения
асимметрия
(skewness)
отклонение от центра
эксцесс
дисперсия (variance)
среднеквадратическое (стандартное)
отклонение
коэффициент вариации
моменты распределения
3.
ЗР исчерпывающе описывают СВи позволяют рассчитать вероятности любых
связанных с ними событий
Однако:
1) Не всегда необходимы (кто лучше стреляет?)
2) Полное описание относительно громоздко
при естественном стремлении уйти от «много чисел»
к «всего нескольким»
Нужен небольшой набор чисел,
которые описывали бы СВ
лаконично
4.
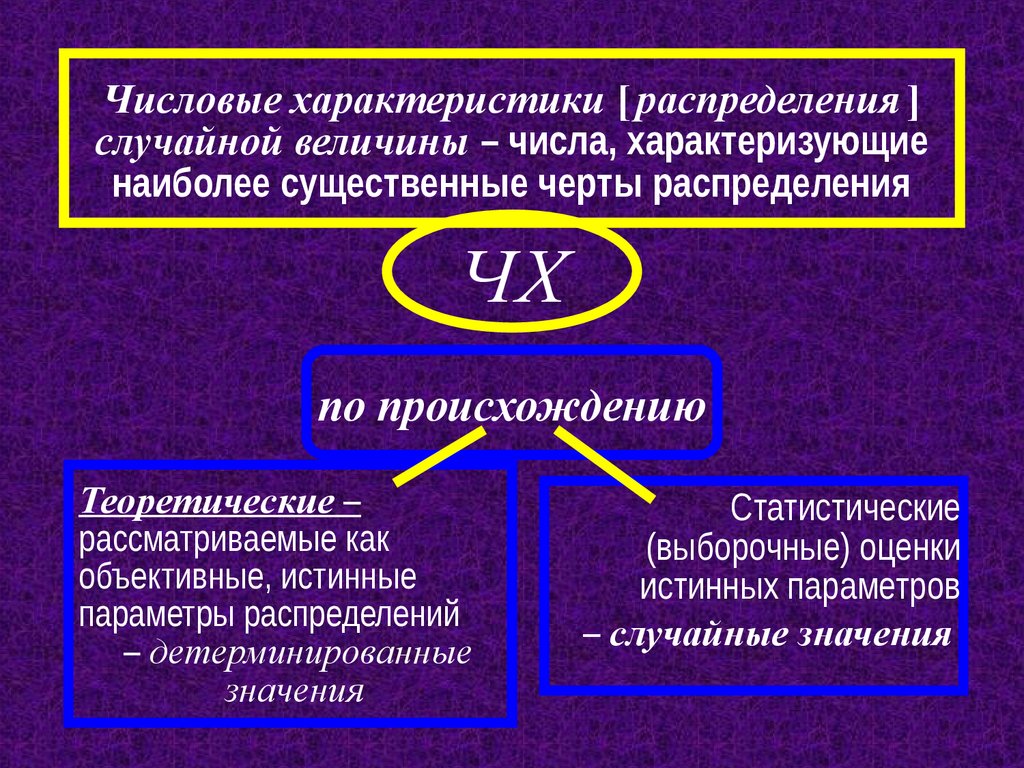
Числовые характеристики [ распределения ]случайной величины – числа, характеризующие
наиболее существенные черты распределения
ЧХ
по происхождению
Теоретические –
рассматриваемые как
объективные, истинные
параметры распределений
– детерминированные
значения
Статистические
(выборочные) оценки
истинных параметров
– случайные значения
5.
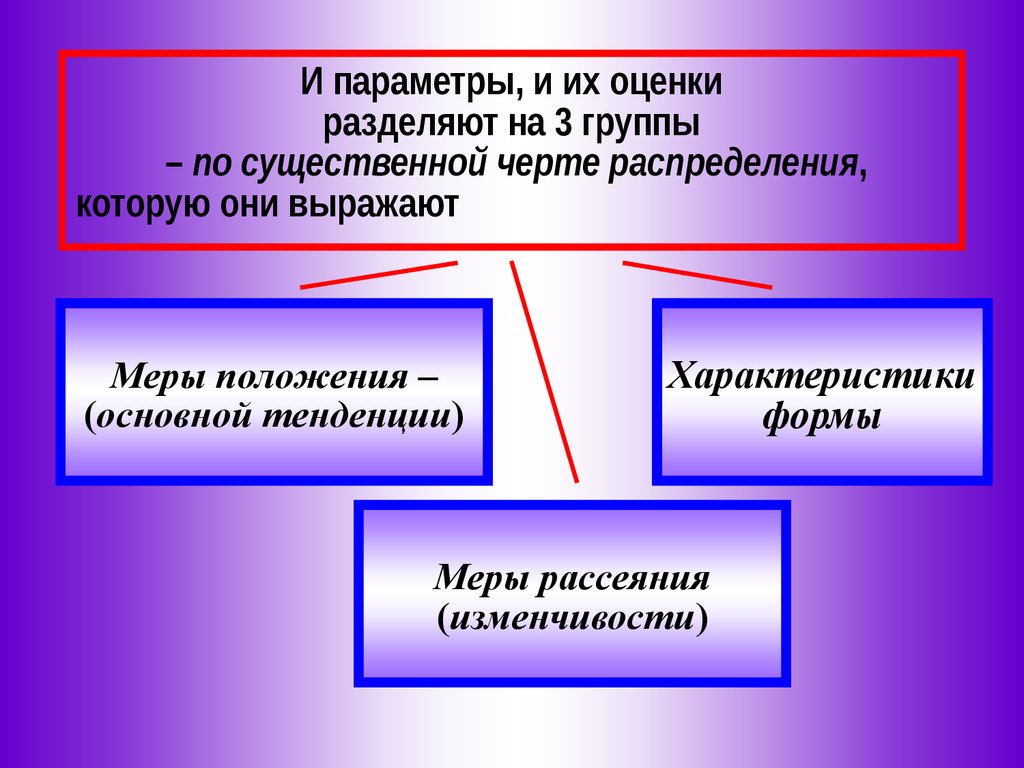
И параметры, и их оценкиразделяют на 3 группы
– по существенной черте распределения,
которую они выражают
Меры положения –
(основной тенденции)
Характеристики
формы
Меры рассеяния
(изменчивости)
6.
Характеристики положенияФиксируют место СВ на числовой оси.
Это некоторое среднее значение,
эталон, место нахождения,
вокруг которого группируются значения СВ
еще называют – «центр группирования», СРЕДНЕЕ
Используются как представители СВ в грубых,
прикидочных расчетах (например…)
Наиболее важное из средних – математическое
ожидание
7.
Математическое ожидание дискретной величиныесть сумма произведений всех ее значений
на вероятности этих значений
m
M ( X ) x1 p1 x2 p2 xm pm xi pi
i 1
Другие обозначения : MX , ,
( E, )
Примеры
8.
ПримерыМ.о. числа очков, выбиваемых 1-ым стрелком:
М(X) = 1 0.0 + 2 0.2 + 3 0.8 = 2.8
М.о. числа очков, выбиваемых 2-ым стрелком:
М(Y) = 1 0.2 + 2 0.5 + 3 0.3= 2.1
Для любой биномиальной величины M = np
3.0
М.о. числа попаданий при n = 4 выстрелах
с вероятностью попасть в каждом p = 0.75
?
9.
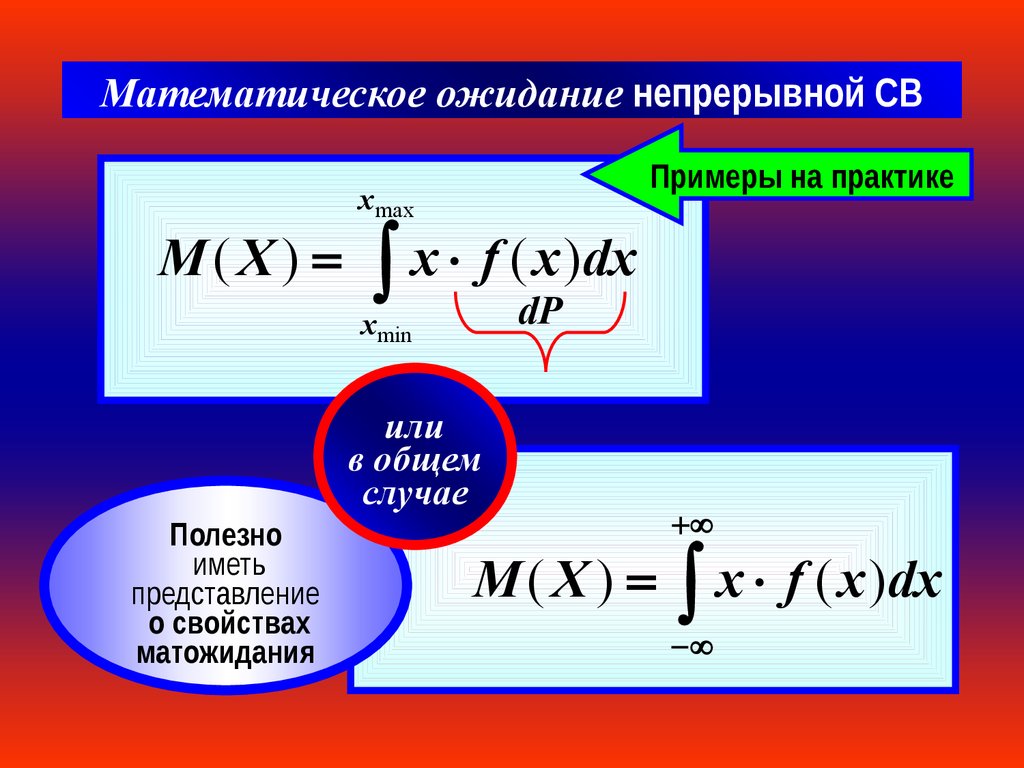
Математическое ожидание непрерывной СВM(X)
Примеры на практике
xmax
x f (dPx )dx
xmin
или
в общем
случае
Полезно
иметь
представление
о свойствах
матожидания
M(X)
x
f
(
x
)
dx
10.
Мода и МедианаДругие характеристики
центра
Mo – значение величины X, которому соответствует
максимальная плотность распределения.
Для дискретной X – наиболее вероятное значение
f(Mo) = max f(x)
Mo = x{pi max}, i = 1, …, m
Me – значение величины X, для которого
вероятность меньших значений равна вероятности больших
F(Me) = 0.5
11.
3Унимодальное распределение
2
Mo
1
Me
0
0
1.5
x
про
площади
0.5
1
Бимодальное распределение
1
0.5
0
0
0.5
x1
12.
Рассмотрели характеристики центра:матожидание М или
моду Мо
медиану Ме
Рассматриваем характеристики
рассеяния разброса, изменчивости,
вариации
13.
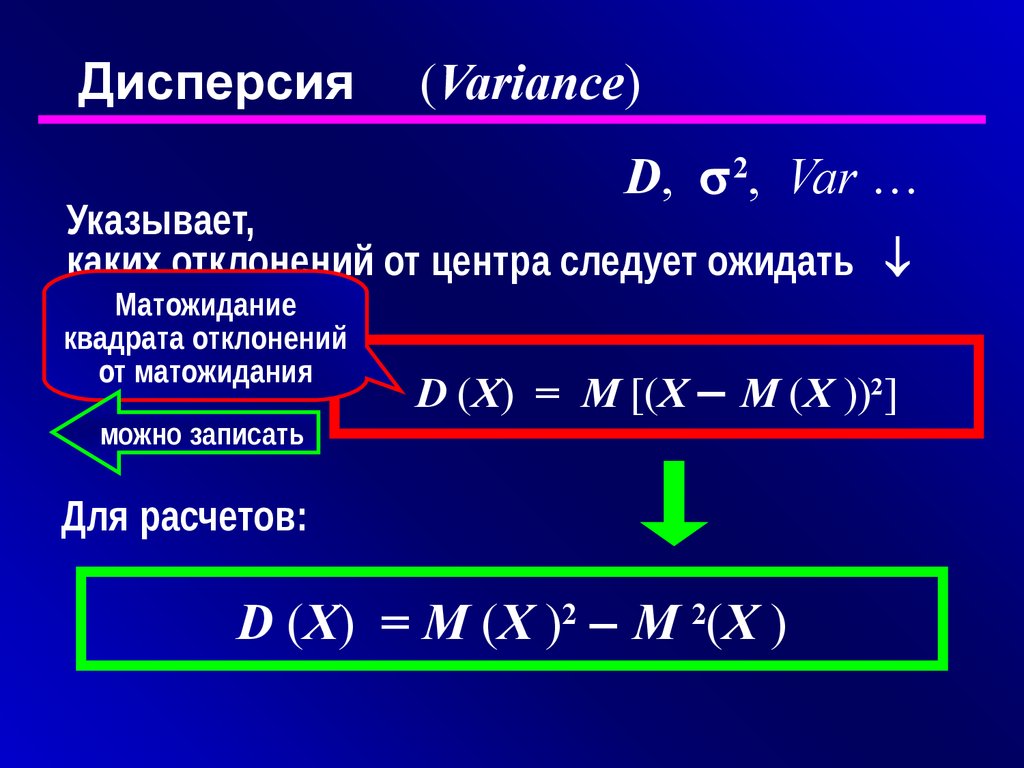
Дисперсия(Variance)
D, 2, Var …
Указывает,
каких отклонений от центра следует ожидать
Матожидание
квадрата отклонений
от матожидания
можно записать
D (X) = M [(X M (X ))2]
Для расчетов:
D (X) = M (X )2 M 2(X )
14.
Дисперсия дискретной СВ:m
D( X )
j 1
Дисперсия
непрерывной
СВ:
DX
2
xj pj
2
M (X )
2
DX x f
xmax
x
xmin
2
2
( x)dx M X
f ( x )dx M
2
X
15.
Был пример про стрелков:значения дисперсии показали 1-ый
стреляет «кучнее», у него разброс
попаданий меньше
Проверьте!
16.
Важный примерПрименение общей формулы в случае
биномиального распределения
дает:
D = n p q
Например:
дисперсия количества попаданий
при 4-х независимых выстрелах и вероятности
попасть в каждом 0.75 равна
D = 4 0.75 0.25 = 0.75
17.
Пример непрерывной величиныИзвестно, что плотность распределения f(x) = 1/4
в интервале от 40 до 44.
Тогда:
44
2
3 44
x
x
4
2
2
D
dx 42
42
4
12 40
3
40
18.
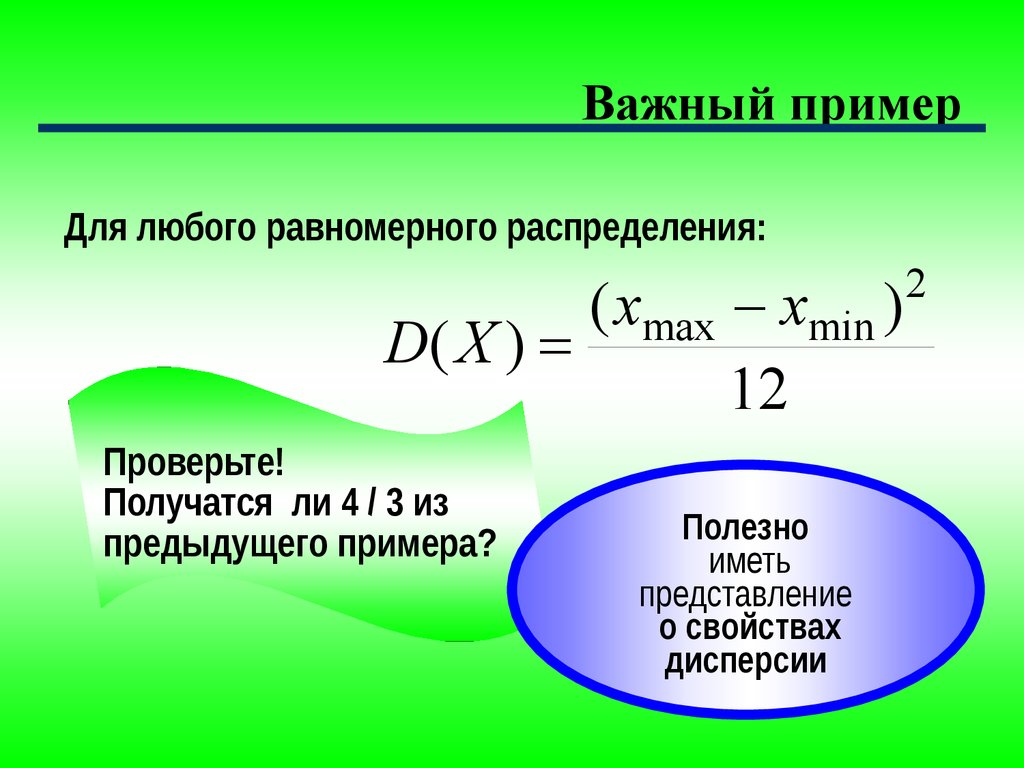
Важный примерДля любого равномерного распределения:
( xmax xmin )
D( X )
12
Проверьте!
Получатся ли 4 / 3 из
предыдущего примера?
Полезно
иметь
представление
о свойствах
дисперсии
2
19.
Более естественная мера разбросаимеет ту же размерность, что и СВ
это корень квадратный из дисперсии
D
среднеквадратическое
(стандартное)
отклонение
«Физический смысл» :
показывает, как далеко в среднем
отдельные значения отклоняются от их центра
20.
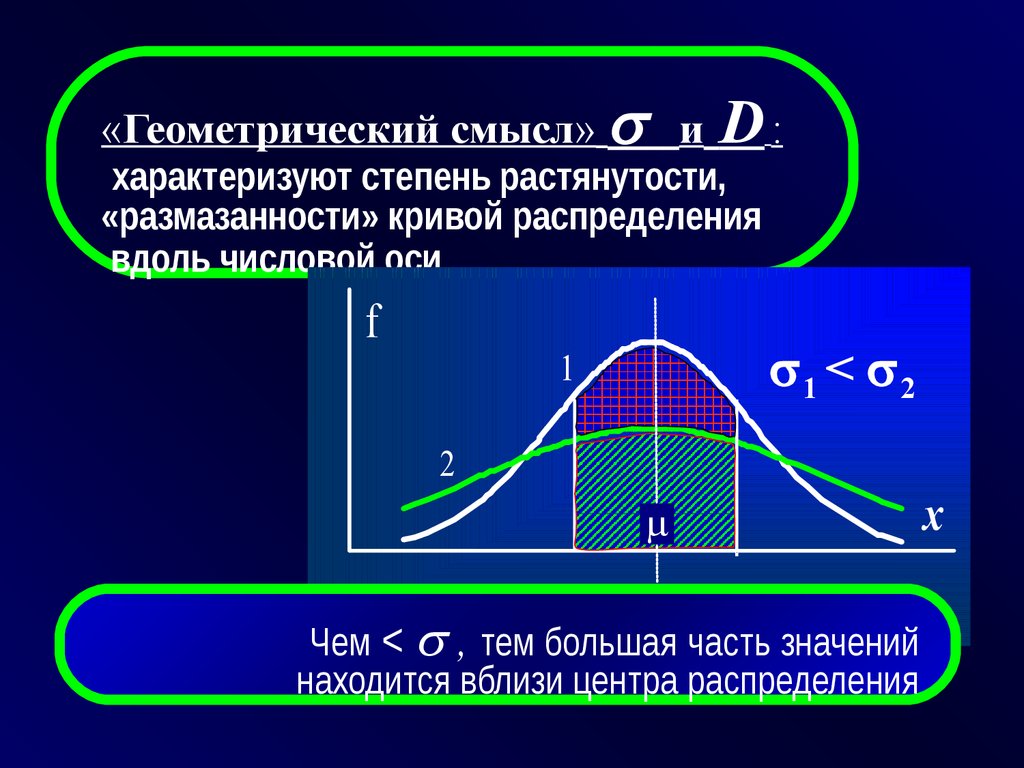
«Геометрический смысл» иD:
характеризуют степень растянутости,
«размазанности» кривой распределения
вдоль числовой оси
f
1 < 2
1
2
Чем < , тем большая часть значений
находится вблизи центра распределения
x
21.
Отклонения от центра отдельных значений38
попугаев!
иногда измеряются в «сигмах»
x
z
нормализованное (стандартизованное)
отклонение
22.
Еще одна характеристикаизменчивости
коэффициент вариации
Мера относительного рассеяния
полезна при сравнении СВ,
особенно одних и тех же
параметров но разных объектов
v
[100%]
Пример
Одно и то же стандартное отклонение веса в 0.5 кг
было бы большим для группы младенцев,
но очень небольшим для студентов.
Это видно по коэффициенту вариации
v (млад) = 0.5/3.5 > 14 % v (студ) = 0.5/65 < 0.8 %
23.
Моменты распределенияТак называют параметры
распределений по аналогии
с механикой
Математическое ожидание
начальный
момент 1-го порядка
Дисперсия D центральный
момент 2-го порядка
С моментами более высоких порядков связаны
характеристики формы распределения
24.
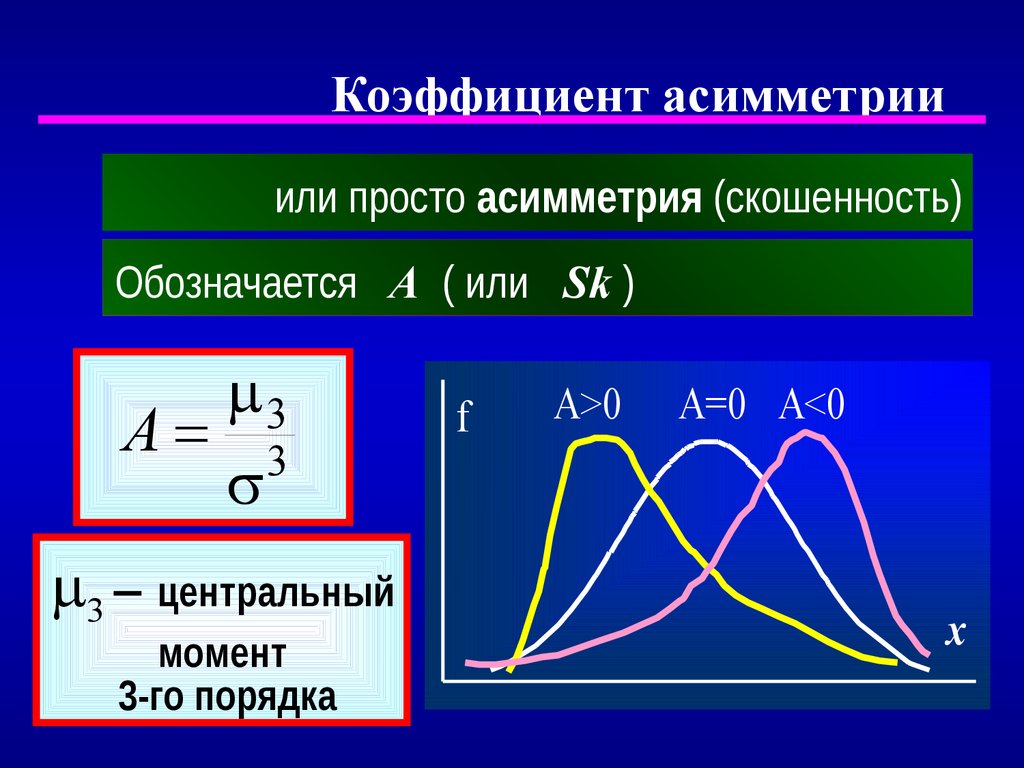
Коэффициент асимметрииили просто асимметрия (скошенность)
Обозначается А ( или Sk )
3
A 3
3 центральный
момент
3-го порядка
f
A>0
A=0 A<0
x
25.
Коэффициент эксцессаили просто эксцесс
4
E 4 3
4 центральный
момент
4-го порядка
Обозначается E
Что за «3»?
f
E>0
E=0
E<0
x
26.
А и Епозволяют судить
об отклонении распределения
от «стандарта» нормального закона
распределения
The
End
The End


















 Математика
Математика








