Похожие презентации:
Случайная величина
1. Случайная величина
• Случайная величина – это переменная,которая принимает свои значения в
зависимости от случайных обстоятельств.
• .Дискретная случайная величина
(точечная) принимает отдельные
• числовые значения (кубик: 1,2,3,4,5,6)
• Непрерывная случайная величина
принимает любые значения из
некоторого интервала
(рост студентов).
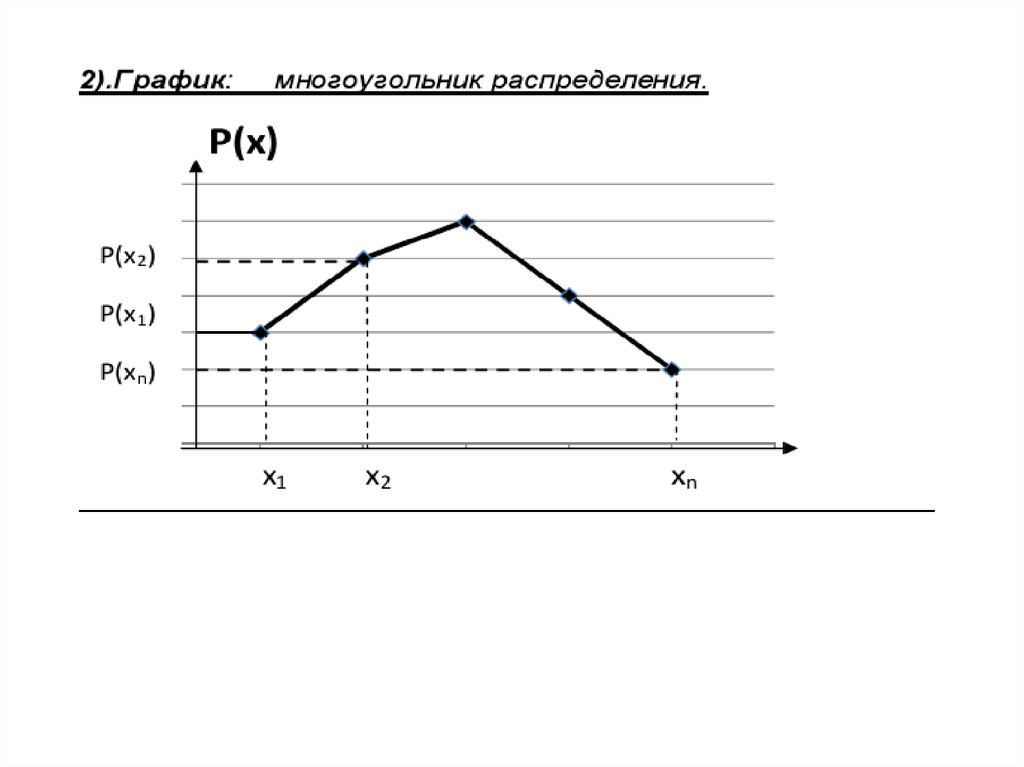
2. Закон распределения случайной величины
Это связь между возможными значениямислучайной величины и вероятностями, с
которыми она эти значения принимает,
в виде 1) таблицы 2) графика 3) функции
распределения
• Дискретная случайная величина.
• Таблица
Условие нормировки
X
x1
x2
P(x)
P(x1) P(x2)
…
xn
P(xn)
3.
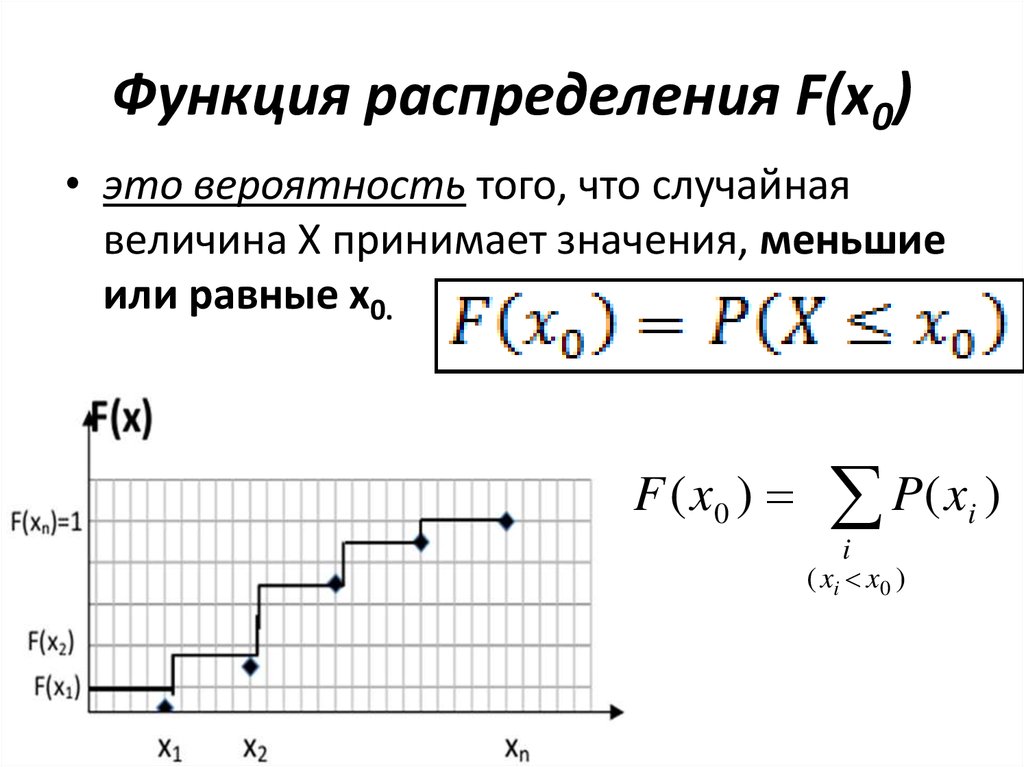
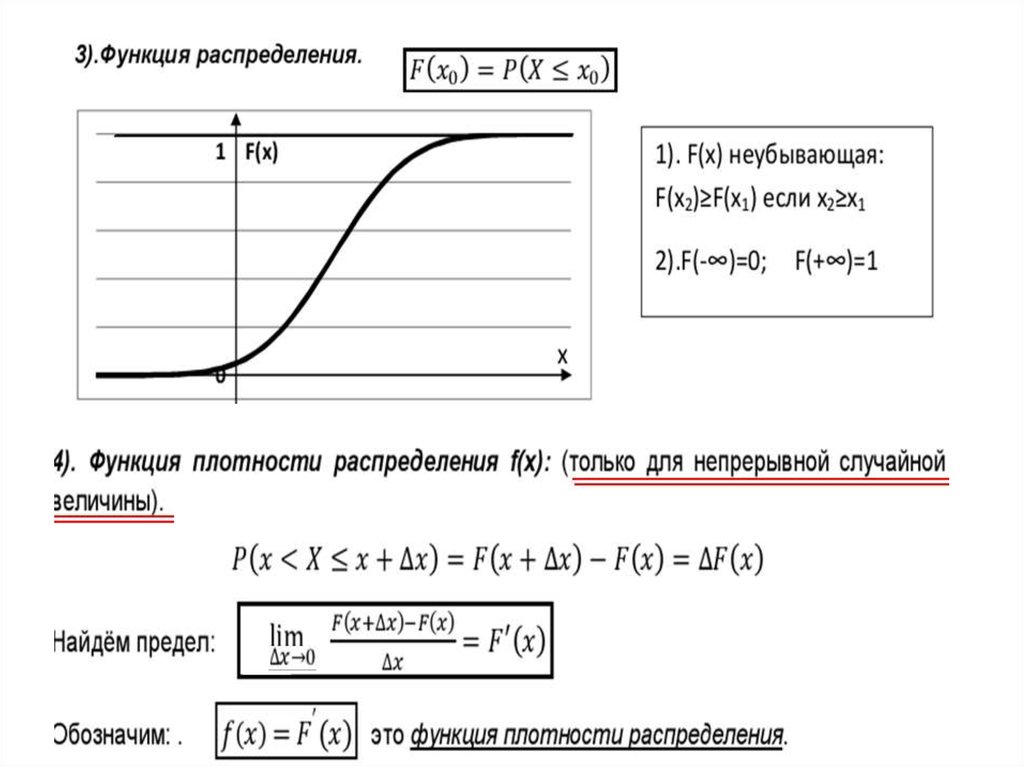
4. Функция распределения F(x0)
• это вероятность того, что случайнаявеличина X принимает значения, меньшие
или равные x0.
F ( x0 )
P( x )
i
i
( xi x0 )
5. Свойства функции распределения
1). F(x) неубывающая: F(x2)≥F(x1)если x2≥x1
2).F(-∞)=0;
F(+∞)=1
Вероятность попадания значения
случайной величины в заданный интервал
6.
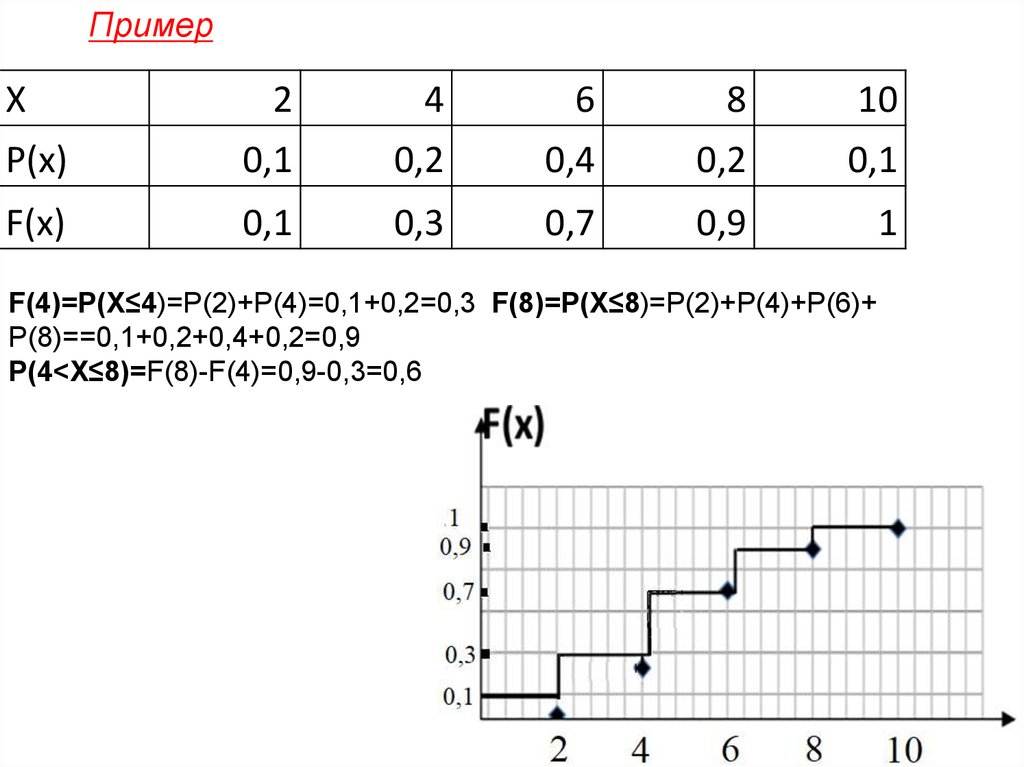
ПримерX
2
4
6
8
10
P(x)
0,1
0,2
0,4
0,2
0,1
F(x)
0,1
0,3
0,7
0,9
1
F(4)=P(X≤4)=P(2)+P(4)=0,1+0,2=0,3 F(8)=P(X≤8)=P(2)+P(4)+P(6)+
P(8)==0,1+0,2+0,4+0,2=0,9
P(4<X≤8)=F(8)-F(4)=0,9-0,3=0,6
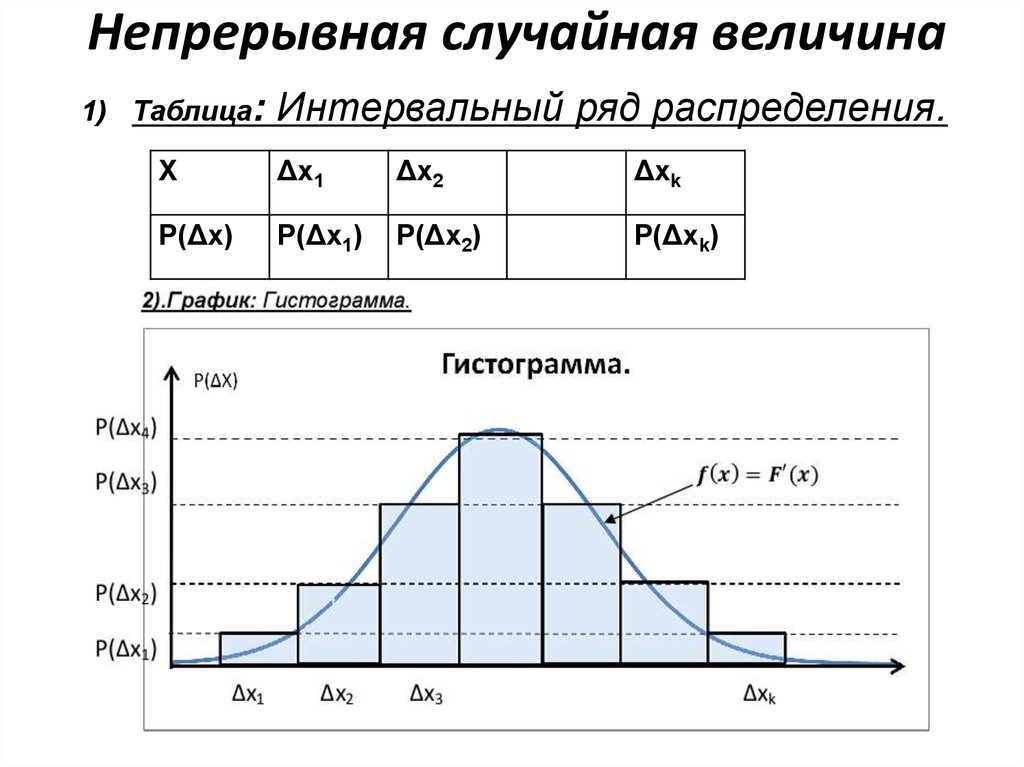
7. Непрерывная случайная величина
1) Таблица:Интервальный ряд распределения.
X
Δx1
Δx2
Δxk
P(Δx)
P(Δx1)
P(Δx2)
P(Δxk)
8.
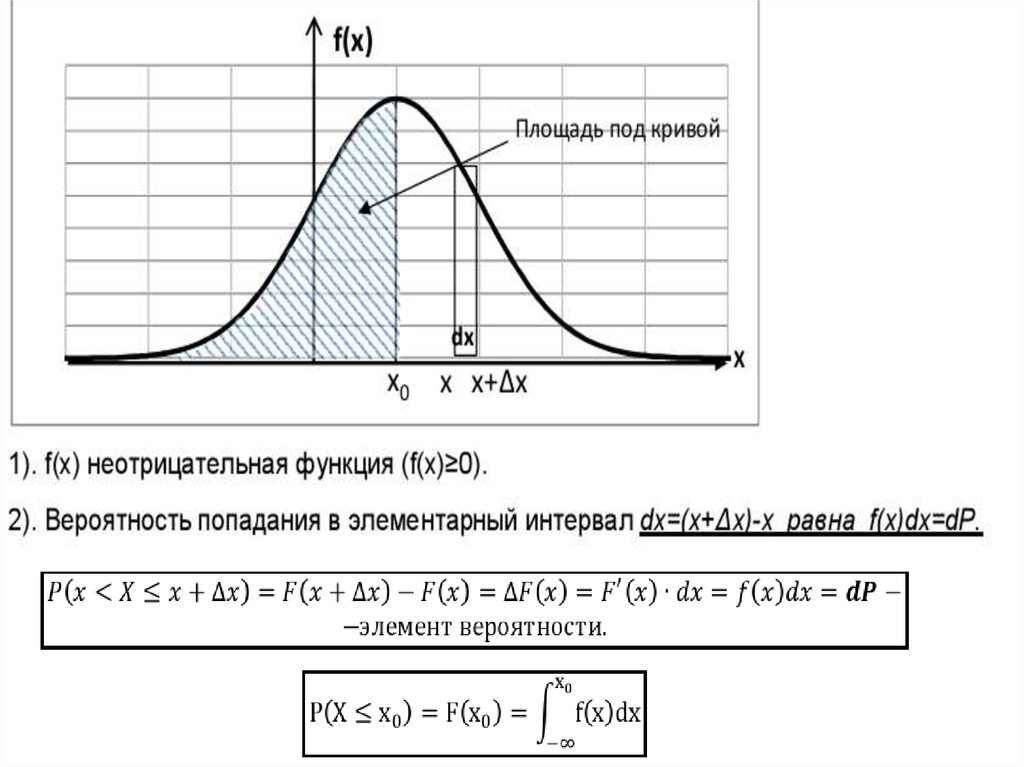
9. Функция плотности вероятности
10.
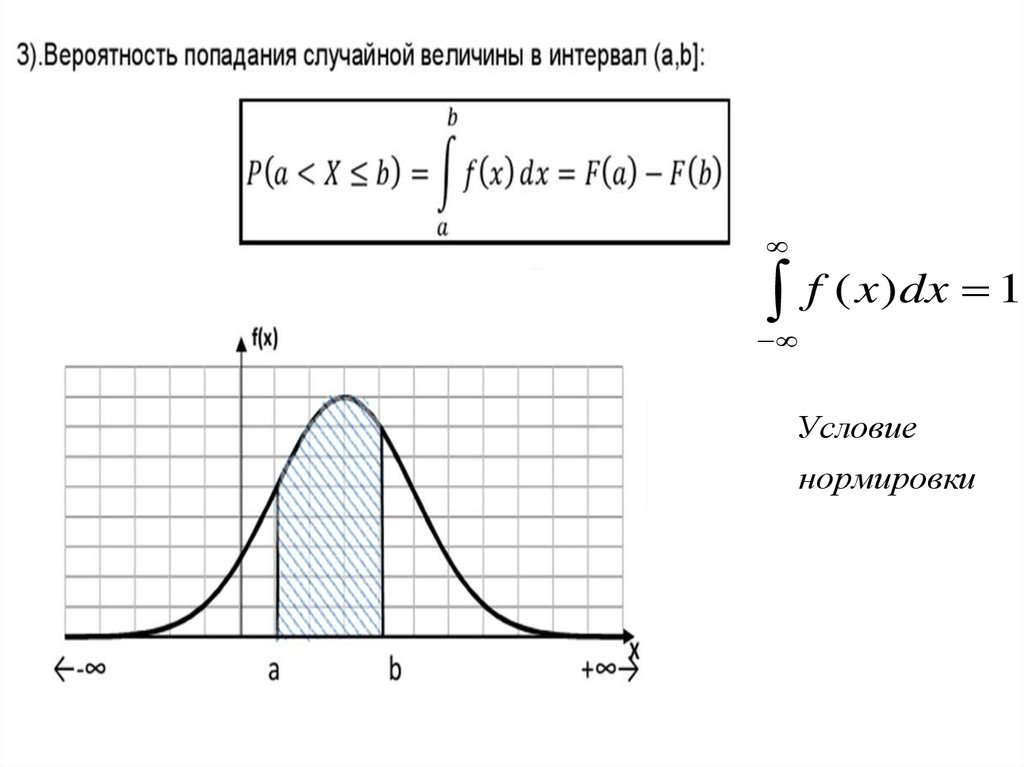
f ( x)dx 1Условие
нормировки
11. Числовые характеристики случайной величины.
1) Математическое ожидание. Это среднее значение случайной величины• Дискретная величина
• Пусть проведено n испытаний, случайная величина приняла значение
• x1 -- m1 раз, x2 -- m2 раз И так далее
x1 x2 xn x1 m1 x2 m2 k
X
xi p ( xi )
n
n
i 1
При n
X M [ x]
математическое ожидание
Непрерывная величина
12. Числовые характеристики случайной величины.
• 2) Дисперсия (рассеивание). Это математическое ожидание (среднеезначение) квадрата отклонения случайной величины X от её
математического ожидания
Дискретная величина
Для удобства
вычислений
Непрерывная величина
13. Числовые характеристики случайной величины
• Если X и Y независимые случайныевеличины,то
Так как размерность дисперсии не совпадает с размерностью
самой случайной величины (например, метры и квадратные
метры), используют
3) Среднеквадратическое или стандартное отклонение
14. Законы распределения дискретной случайной величины. Биномиальное распределение
• Пусть производится N независимыхопытов(бросаем кубик 4 раза)
• В каждом опыте с одной и той же
вероятностью р может наступить событие А
(выпадание грани 6 ; р=1/6)
• Случайная величина - это число k наступлений события A в N опытах (грань 6
выпадает в 4 опытах 2 раза)
15. Биномиальное распределение
• Вероятность такой случайной величинывычисляют по формуле P N , k C k p k q N k
N
N
!
k
где q=1-p ; C N
; к!=1•2• • •к факториал
k! N k !
Таблица биномиального распределения
k
0
1
...
N
P
P(N,0)
P(N,1)
...
P(N,N)
16.
17. Задача господина де Мере
P N , k CNk p k q N k0
4
4
4! 1 1
1 2 3 4 5
625
P(4,0)
0,482
1
0 ! 4! 6 6 1 1 2 3 4 6 1296
1
4!
1 1
P(4,1)
1
01! (4 1) ! 6 6
Сколько раз из
4 бросаний выпадет грань 6
Вероятность
этого события
0
625
1296
4 1
1
500
1296
1
1296
1 2 3 4 1 5
500
0,385
1 1 2 3 6 6 1296
1
2
150
1296
3
20
1296
3
4
1
1296
18. Распределение Пуассона Редкие события
• Если количество испытаний достаточно велико (N), авероятность появления события в отдельно взятом
испытании p весьма мала (0,05-0,1 и меньше), то
вероятность того, что в данной серии испытаний
событие появится ровно k раз, можно приближенно
вычислить по формуле Пуассона:,
k
P k e , k 0,1,2...
k!
где
параметр распределения- среднее число событий
19.
• Если в биномиальном распределении зафиксировать k , а Nувеличивать таким образом, чтобы произведение оставалось
постоянным и равным , то получим распределение Пуассона
• Пример
k
P k e , k 0,1,2...
k!
• На 1000 человек в среднем приходится 1 алкоголик. Найти
вероятность того, что в городке с населением 8000
человек окажется 7 алкоголиков.
• Биномиальное распределение
7
(0,001) 7 (0,999) 8000 7
• P(8000,7) C8000
• Распределение Пуассона
8 7 e 8
P7
0,19
7!
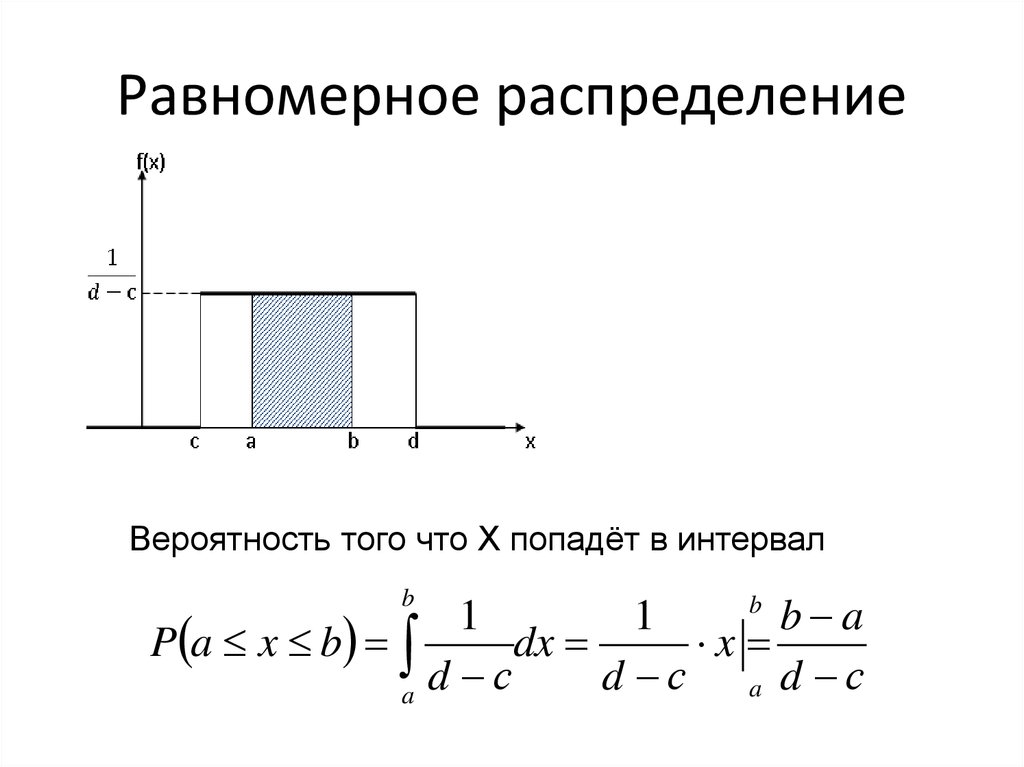
20. Основные законы распределения непрерывной случайной величины
1.Равномерное или прямоугольное распределение.Случайная величина называется равномерно распределённой
на интервале [c,d], если функция плотности распределения
её на этом интервале постоянна, а вне него равна нулю.
const , если c x d
f x
если x с, x d
0
d
d
d
d
d
f x dx f x dx const dx const dx const x const d с 1
с
с
c
const
c
1
d с
c
21. Равномерное распределение
Вероятность того что X попадёт в интервалb
1
1
b a
P a x b
dx
x
d с
d с a d с
a
b
22. Больные попадают на флюорографическое обследование строго по расписанию работы кабинета и интервалом 7 минут. Составить функцию
плотности случайной величины t – времени ожидании приглашения вкабинет больным, который наудачу подошёл к кабинету. Найти
вероятность того, что он будет ждать приглашения не более 3 –х минут.
Вычислим вероятность того, что пассажир будет ожидать приглашения
не более 3 минут:
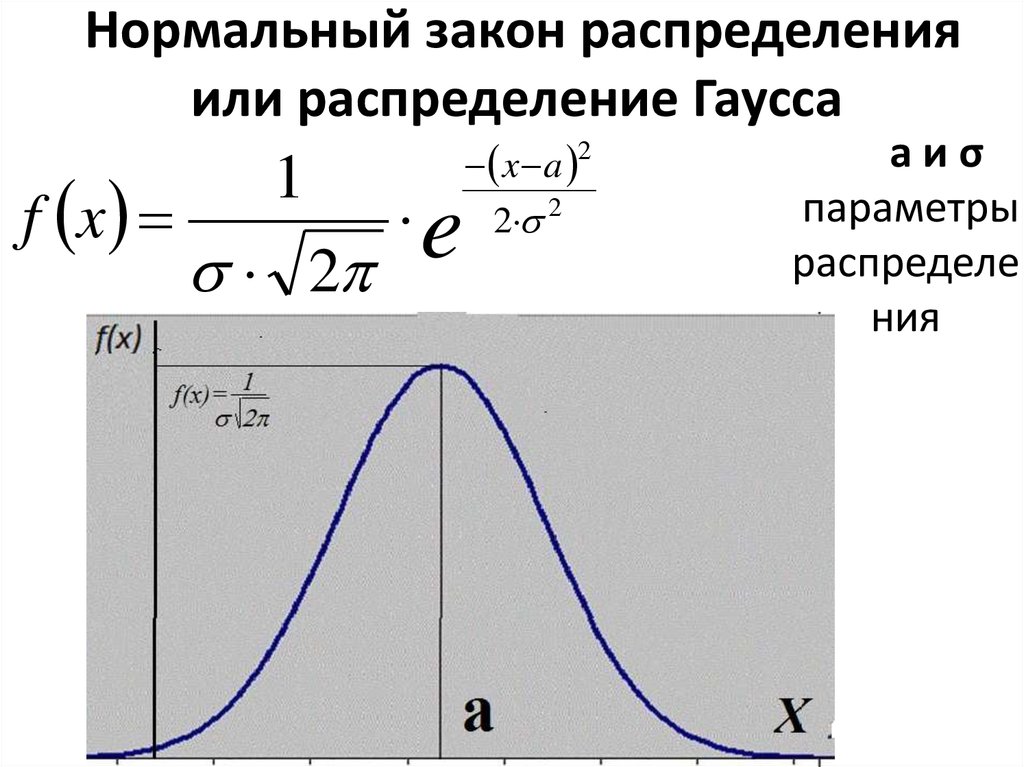
23. Нормальный закон распределения или распределение Гаусса
f x1
2
e
x a 2
2 2
aиσ
параметры
распределе
ния
24. Нормальное распределение
Условиенормировки
f x dx 1
С изменением параметра а кривая смещается по оси х:
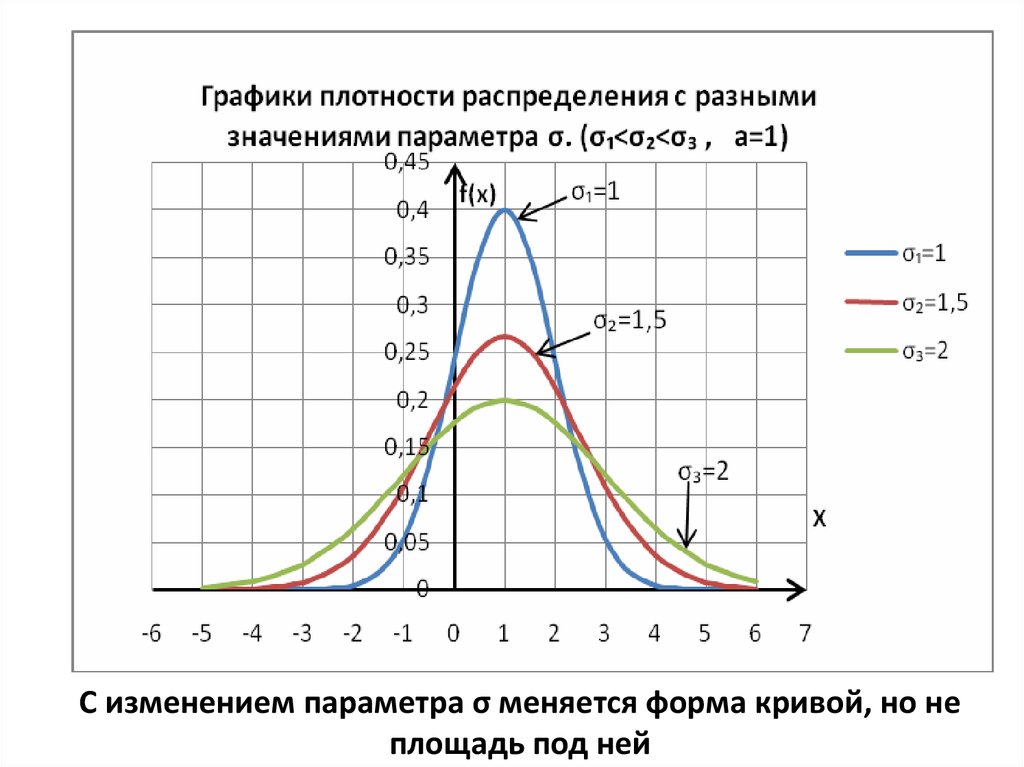
25.
С изменением параметра σ меняется форма кривой, но неплощадь под ней
26. Параметры нормального распределения
математическое ожиданиеM X x f x dx
1
2
x
e
x a 2
2
2
dx a
дисперсия.
D x
x M x
2
f x dx
1
x a 2
2
x
a
e
2
2
2
dx 2
D – среднее квадратическое отклонение.
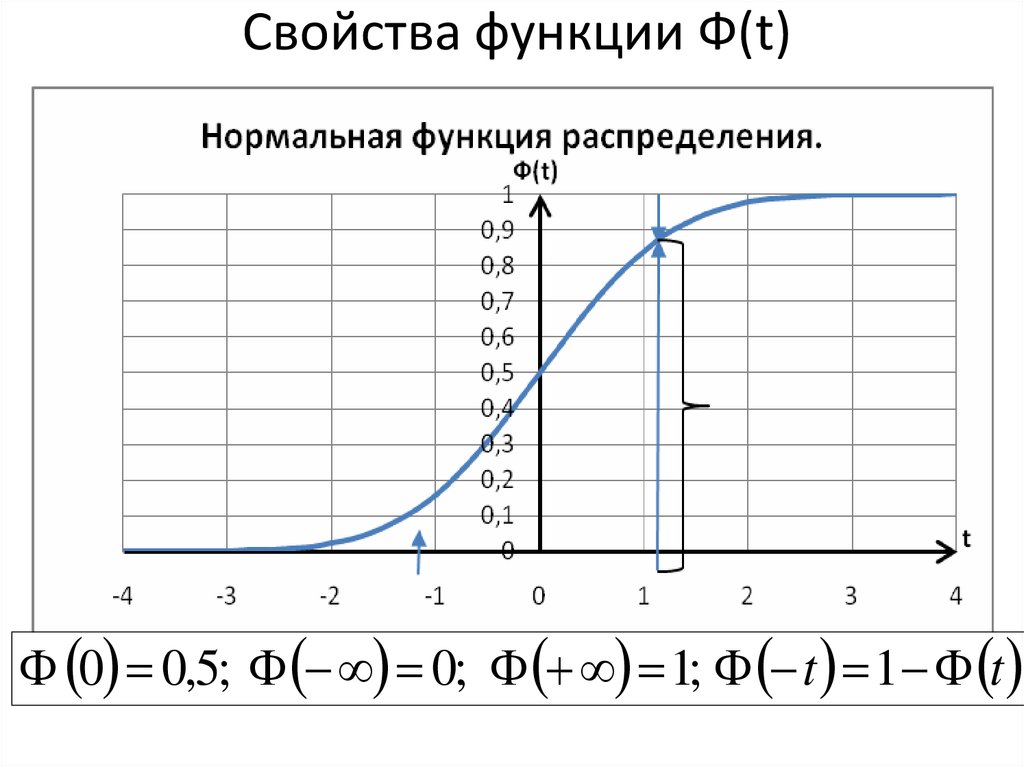
27. Нормальная функция распределения
F x P , xx
f x dx
x
1
2
e
• Введём замену переменной:
t
x a
1
2
x M X
X
t
e
t 2
2
dt
1
dx
x M X
dt t
X
x a 2
2
2
dx
28. Свойства функции Ф(t)
0 0,5; 0; 1; t 1 t29.
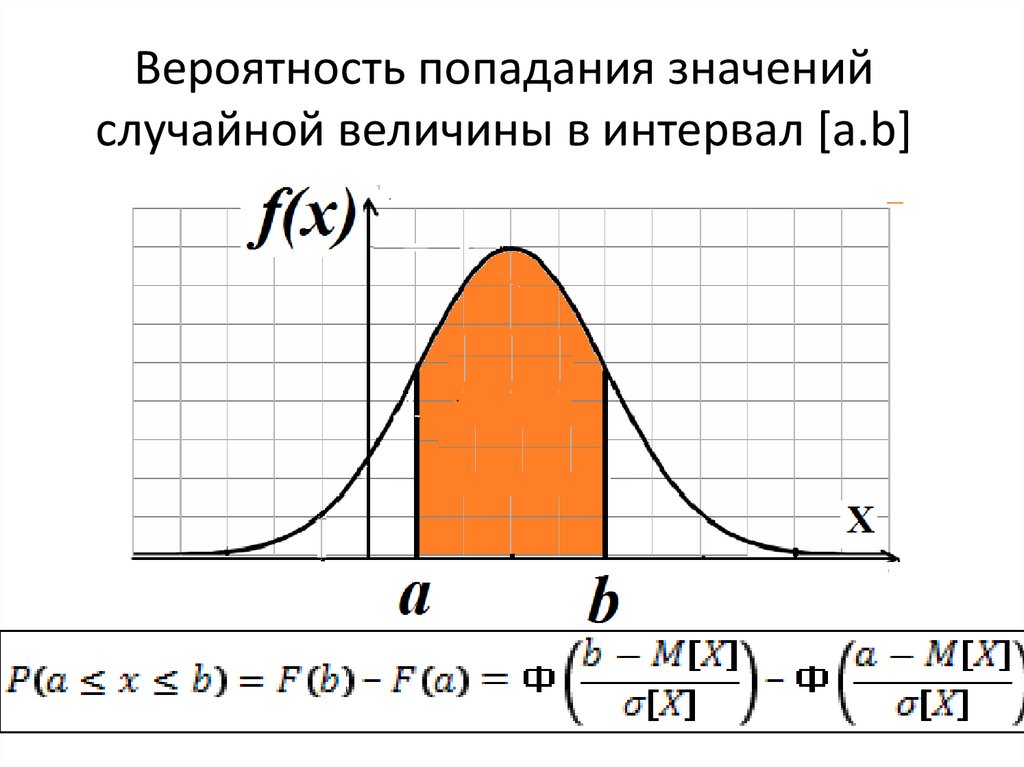
Вероятность попадания значенийслучайной величины в интервал [a.b]
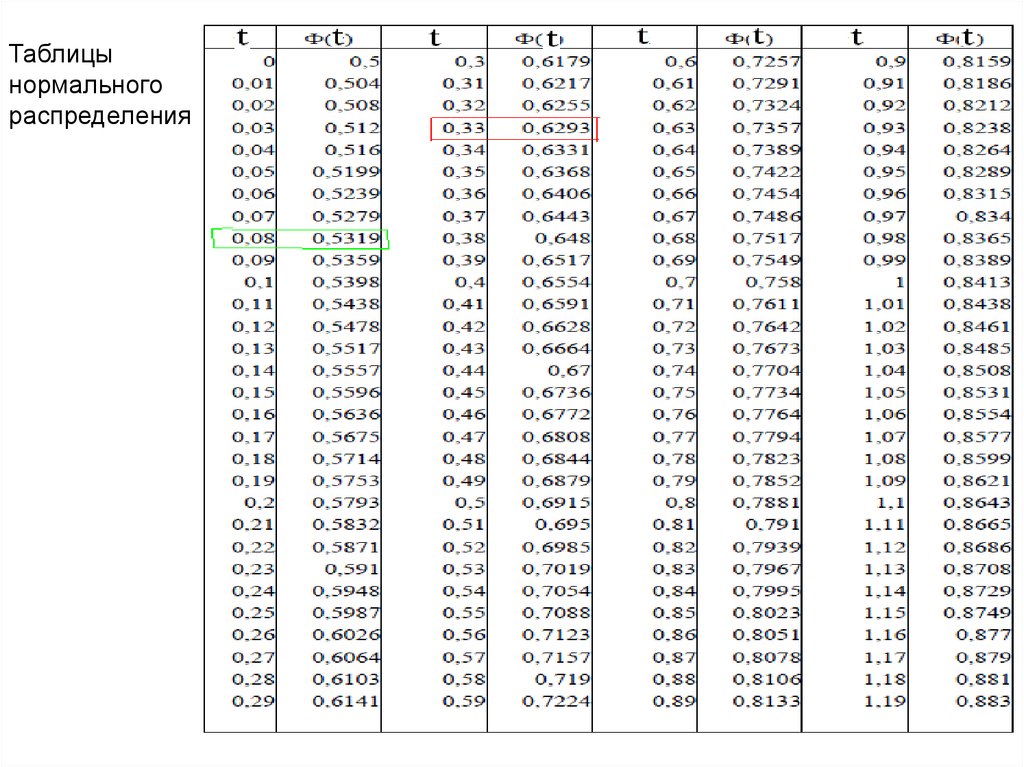
30. Таблицы нормального распределения
Таблицы нормального распределения31. Пример 1
• Случайная величина распределена по нормальномузакону. Параметры распределения:a=4, σ=3. Найти
вероятность того, что случайная величина попадёт в
интервал от (- ∞ ) до 5
x a 5 4
t2
0,33
3
4
t1
3
5 4
P( x 5) F (5) F ( )
3
0,33 0 0,62
32. Пример 2
Случайная величина распределена по нормальному закону. Параметры распределения:a=4, 3• Чему равно х, если
P( X x) 0,53
x a
x 4
P ( X x ) F ( x )
0,53
3
• По таблице находим: для
x 4
(t ) 0,53 t 0,08
0,08
3
0,24 x 4
x 4,24
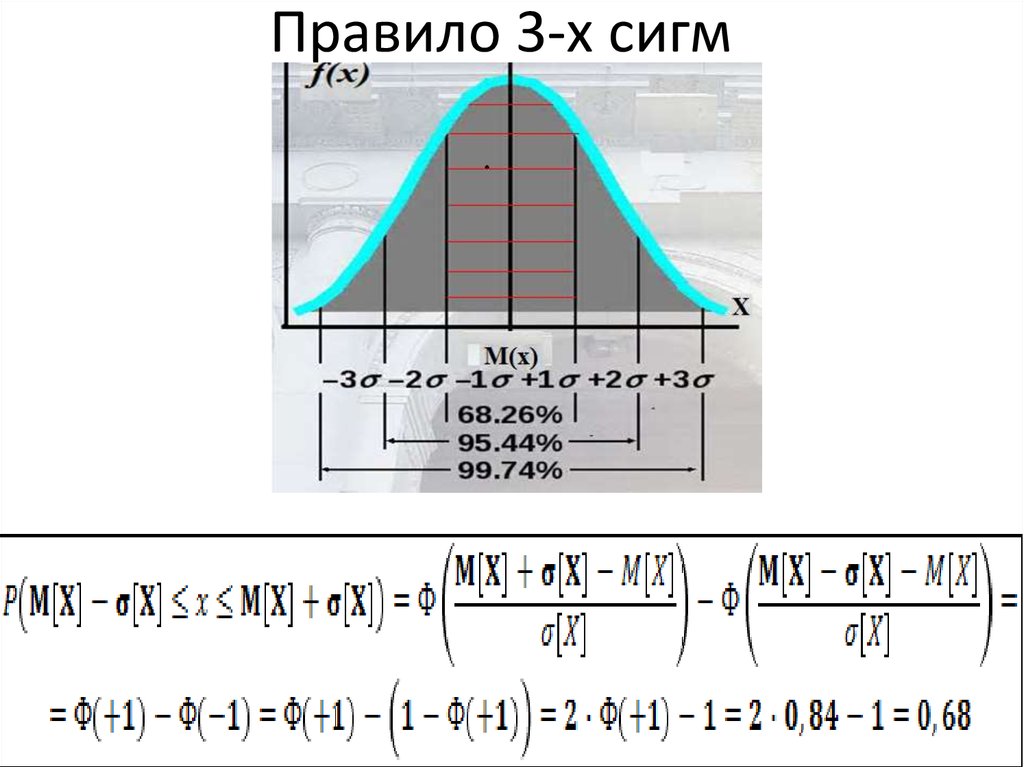
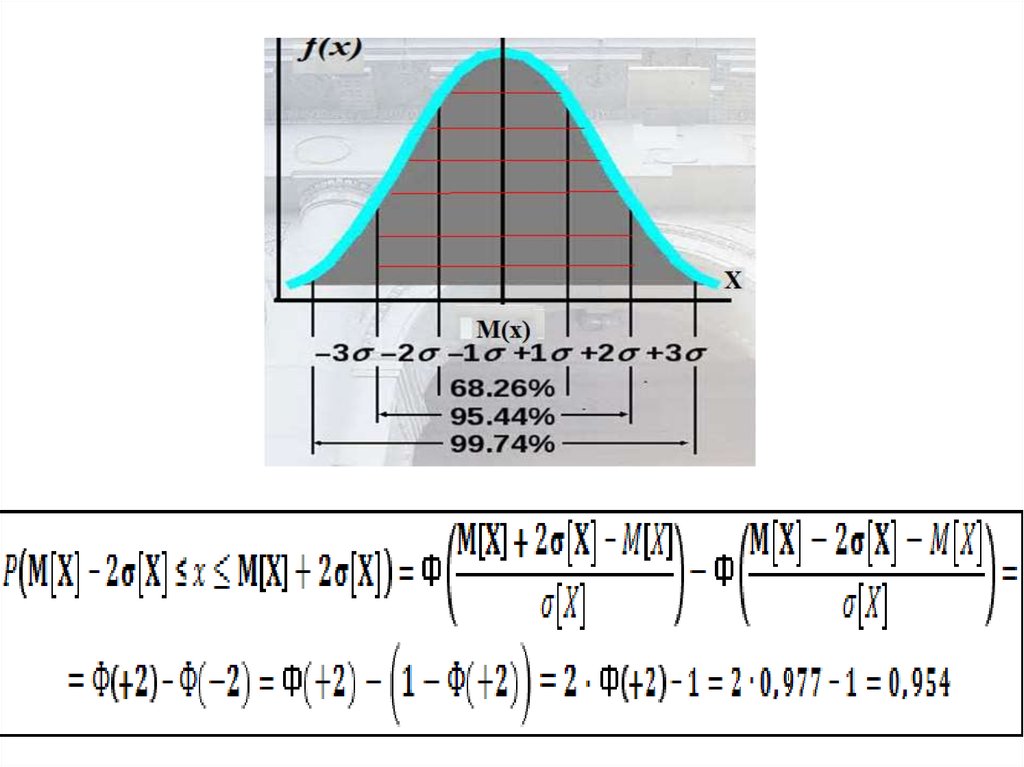
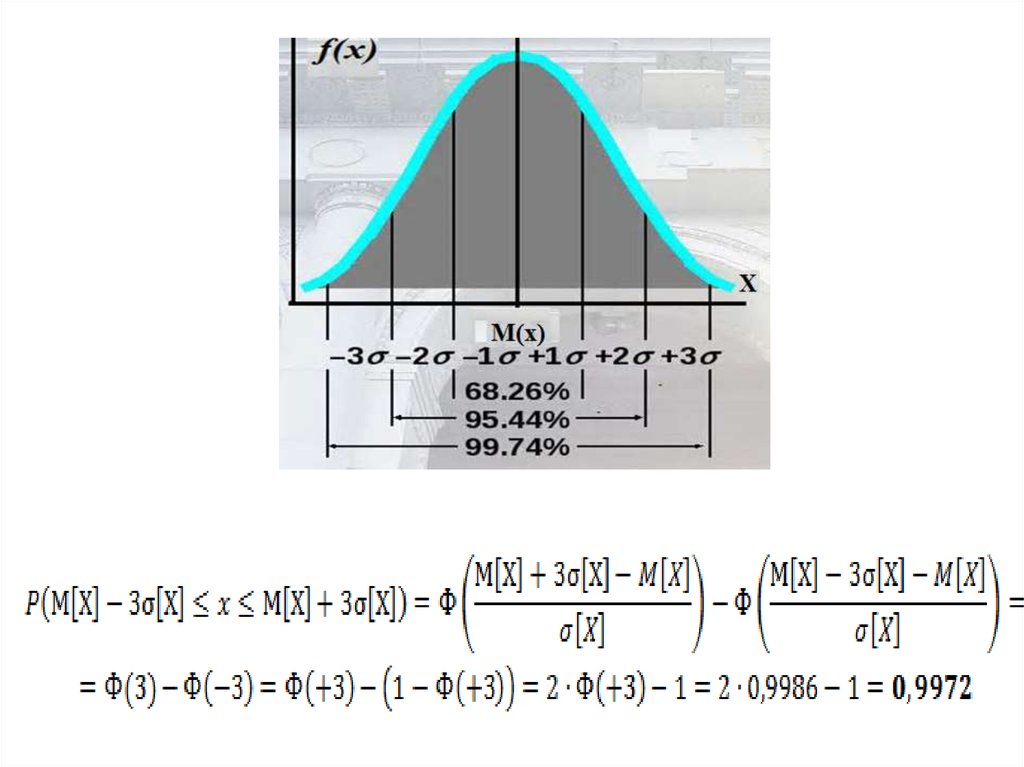
33. Правило 3-х сигм
34.
35.
36. Математическая статистика.
Статистическая совокупность – это множествообъектов, обладающих общими признаками, которые
являются наиболее важными (типичными) для
характеристики этих объектов.
Объём совокупности n –это число членов совокупности
Генеральная совокупность – это совокупность всех
объектов, которые имеют типичную характеристику или
признак. Это все возможные значения случайной величины.
Объём генеральной совокупности).
Выборочная совокупность (выборка) – это отобранная
тем или иным способом часть генеральной совокупности
Варианта – это числовое значение изучаемого признака
( отдельные значения случайной величины )
37. Основные задачи, которые стоят перед математической статистикой
•Определение закона распределения случайнойвеличины по имеющимся статистическим данным (
по выборке – закон распределения для всей
генеральной совокупности).
•Определение неизвестных параметров
распределения ( по выборке оценить параметры
генеральной совокупности).
•Задача проверки правдоподобия выдвигаемых
статистических гипотез
38. Сбор экспериментальных данных.
1) Получаем статистический ряд –совокупность числовых данных или выборку
объёмом n:
2) Производим ранжирование -- это
расположение всех имеющихся вариант
по возрастанию
Пример: при измерении частоты пульса у 10
пациентов получены следующие результаты:
90, 110, 65, 80, 90, 60, 70, 80, 70, 80
Ранжированный ряд имеет вид: 60, 65, 70, 70, 80,
80, 80, 90, 90, 110.
39.
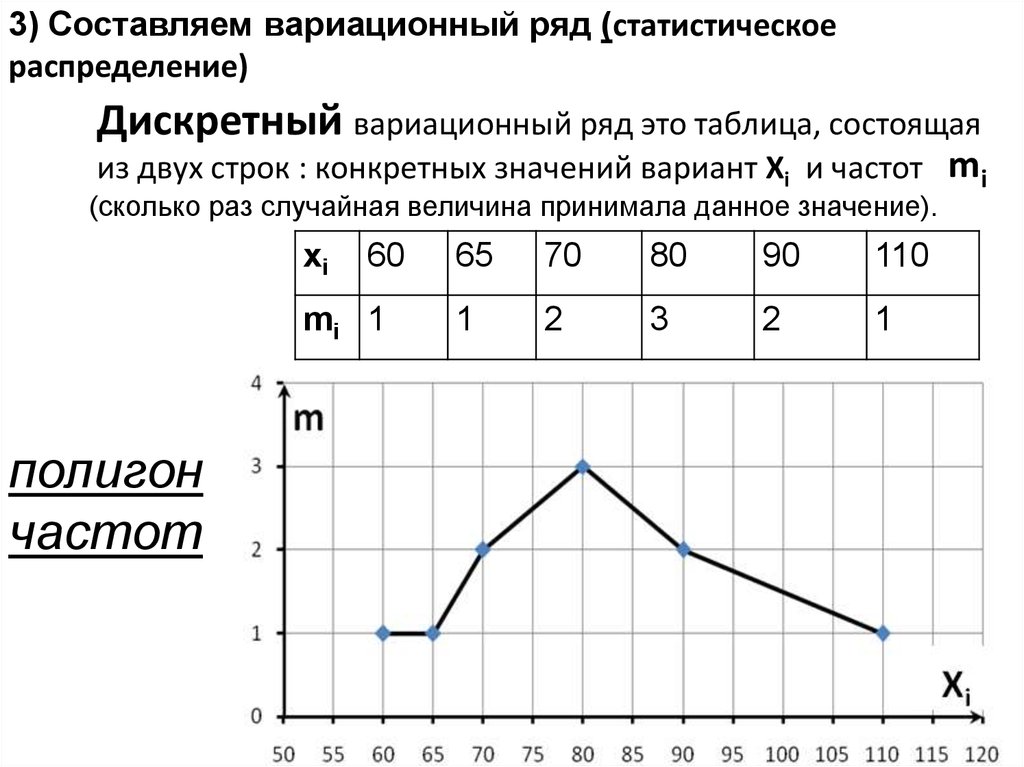
3) Составляем вариационный ряд (статистическоераспределение)
Дискретный вариационный ряд это таблица, состоящая
из двух строк : конкретных значений вариант Xi и частот mi
(сколько раз случайная величина принимала данное значение).
xi
60
mi 1
полигон
частот
65
70
80
90
110
1
2
3
2
1
40.
Для непрерывной случайной величинысоставляется интервальный вариационный ряд:
Первая строка - интервалы изменения признака,
Вторая строка- частоты, относящиеся к данным интервалам
Число интервалов можно приблизительно определить по
формулам:
.
-берётся целая часть числа.
–(формула Брукса, 1963
Длина интервала ΔX рассчитывается по формуле:
Пример. Анализ веса 60-ти новорожденных дал следующие
результаты:min вес 1,5 кг, max вес 5 кг.
к=7
41.
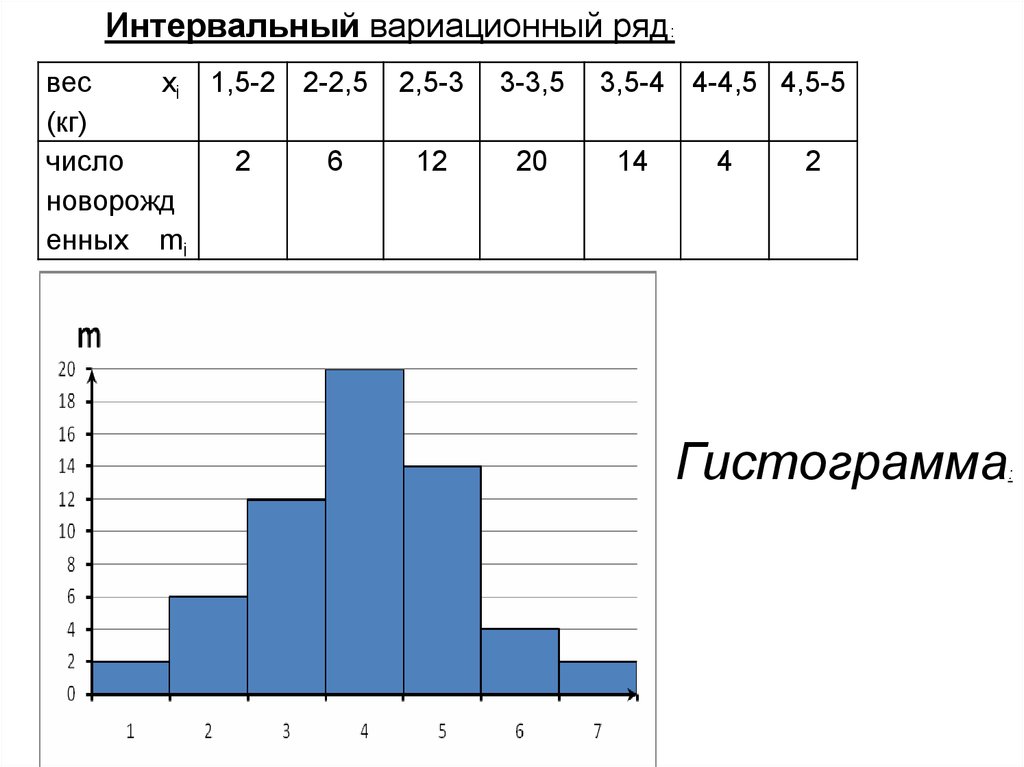
Интервальный вариационный ряд:вес
xi 1,5-2 2-2,5
(кг)
число
2
6
новорожд
енных mi
2,5-3
3-3,5
12
20
3,5-4 4-4,5 4,5-5
14
4
2
Гистограмма
:
42. Статистические характеристики совокупности
Генеральная совокупность (n→∞)Выборка (n- конечно)
Математическое ожидание Среднее арифметическое
n
n
k
x
i 1
n
M X xi P xi
i 1
i
x
n
2
D X xi M X P xi
x
i 1
i 1
Среднее квадратическое
отклонение
X D X
i 1
i
n
Оценка дисперсии
Дисперсия
k
x
i
M X
n
2
n
S n2
x
i 1
i
x
2
n 1
Оценка среднеквадратического
отклонения
S n S n2
43. Ошибка среднего арифметического
Извлечём из генеральной совокупности N выборокодинакового объёма n, тогда их средние
арифметические сами будут являться значениями
случайной величины и имеют отклонения
от
истинного значения М[X].
X x1 . x 2 , ...x N
Ошибка среднего арифметического
S x показывает
насколько близко получаемое по выборке среднее
арифметическое значение, приближается к истинному
среднему М[X] генеральной совокупности
2
n
Sn
Sx
n
x
i 1
i
x
n n 1
44. Интервальные оценки параметров Доверительный интервал
M X x x M X xM X x
f x dx F M X x F M X x
M X x
P M X x x M X x
45.
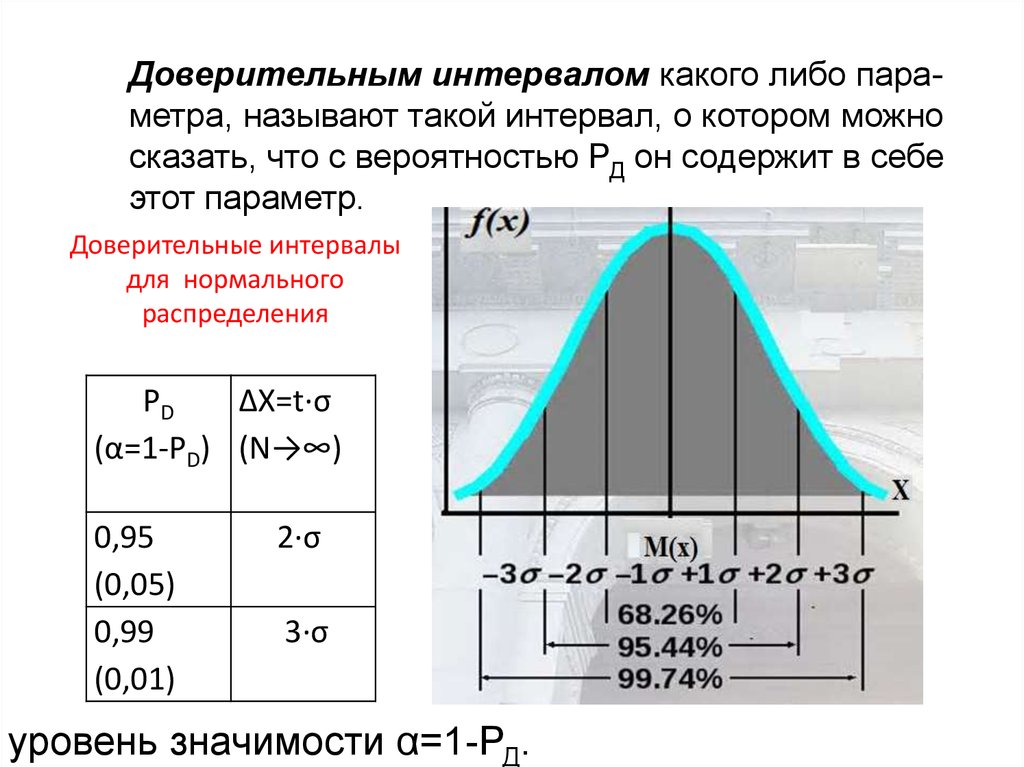
Доверительным интервалом какого либо параметра, называют такой интервал, о котором можносказать, что с вероятностью РД он содержит в себе
этот параметр.
Доверительные интервалы
для нормального
распределения
PD
ΔX=t∙σ
(α=1-PD) (N→∞)
0,95
(0,05)
0,99
(0,01)
2∙σ
3∙σ
уровень значимости α=1-РД.
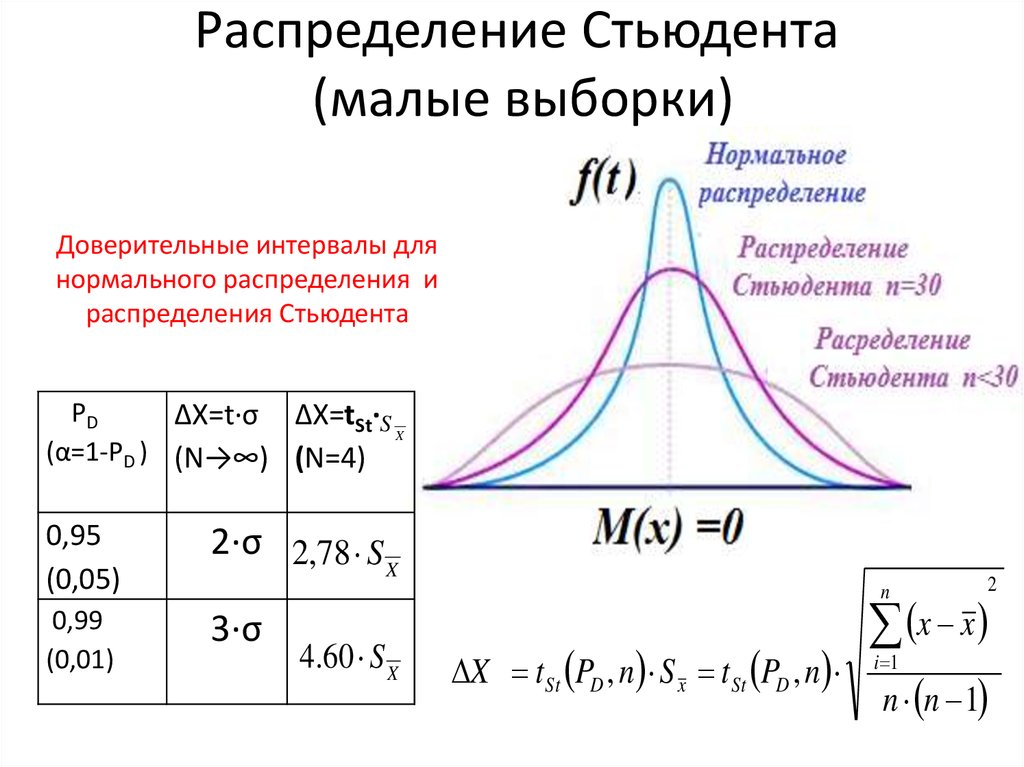
46. Распределение Стьюдента (малые выборки)
Доверительные интервалы длянормального распределения и
распределения Стьюдента
PD
ΔX=t∙σ ΔX=tSt∙S
X
(α=1-PD ) (N→∞) (N=4)
0,95
(0,05)
2∙σ 2,78 S
X
0,99
(0,01)
3∙σ
n
4.60 S X
X t St PD , n S x t St PD , n
2
x x
i 1
n n 1
47.
Пример: При определении концентрации белка в растворебыли получены следующие результаты (в мг/л):110, 112, 115,
113,114. Найти 1) среднее значение,2) стандартное
отклонение и 3)доверительный интервал для Рд=0.95.
48. Алгоритм обработки результатов прямых измерений
• 1) Провести серию измерений,x1 , x2 ,... xN , N 3.
не менее трех
• 2) Найти среднее арифметическое .
x1 x2 x3 ... x N
x
.
N
• 3) Вычислить доверительный интервал
N
xсл t St
x
i 1
i
x
2
N N 1
для заданной доверительной вероятности,
например, PD 0,95.
49. Алгоритм обработки результатов прямых измерений
• 4) Найти систематическую ошибку.• а). если указан класс точности прибора:
xсист
Кл. т.
100%
хшкалы
xсист
Кл. т. хшкалы
100%
б). если класс точности не указан ( например, линейка или
термометр)
5) Вычислить общую ошибку:
.
xобщ x
2
сл .
х
Эту ошибку называют еще абсолютной ошибкой.
2
сист.
50. Алгоритм обработки результатов прямых измерений
• 6) Записать окончательный результат: .x x xобщ , для PD 0,95
•7) Кроме абсолютной ошибки желательно также
найти коэффициент вариации (или относительную
ошибку, выраженную в процентах):
x
%
100 %.
x
51. Контрольные вопросы.
Биномиальное .распределение.
Распределение Гаусса:
а). Параметры распределения.
б). Нормированная случайная величина.
в). Правило трёх сигм.
Основные понятия математической статистики.
Схема предварительной обработки экспериментальных
данных.
Статистические характеристики совокупности.
Ошибка среднего арифметического.
Доверительный интервал и доверительная вероятность.
Распределение Стьюдента.
Обработка прямых измерений































 Математика
Математика








