Похожие презентации:
Тригонометрические формулы и приемы их запоминания
1.
2. УСТНЫЙ СЧЕТ
1.2.
3.
4.
5.
6.
7.
sin 60º
cos (-30º)
sin 405º
tg 0º
ctg 0º
cos π
tg 2 π
3.
Упростите выражение1. cos
2
2. sin (π + α)
Определите знак выражения
1. cos 100º
2. sin (- 50º)
4.
Найдите значение выражениясos 157º cos 97º + sin 157º sin 97º
1
A) 2 ;
C) 1;
B) 0;
3
D)
.
2
5.
Упростите выражение2 sin 65º cos 65º
A) cos130º;
B) cos 50º;
C) sin 50º ;
D) tg 65º
6.
Тригонометрическиеформулы и приемы их
запоминания
7. Притча о трех дамах:
Пошли три дамы гулять. Первая дама,вторая дама и третья дама.
α
sin
cos
30º
1
45º
2
60º
3
8. Притча о трех дамах:
И неожиданно пошел дождь. Все дамыоткрыли зонтики, и одели по паре
калош.
α
sin
cos
30º
45º
60º
1
2
2
2
3
2
9. Притча о трех дамах:
Прогулка была закончена. Перваядама, вторая дама и третья дама
пошли домой.
α
30º
45º
60º
3
2
2
2
1
2
sin
cos
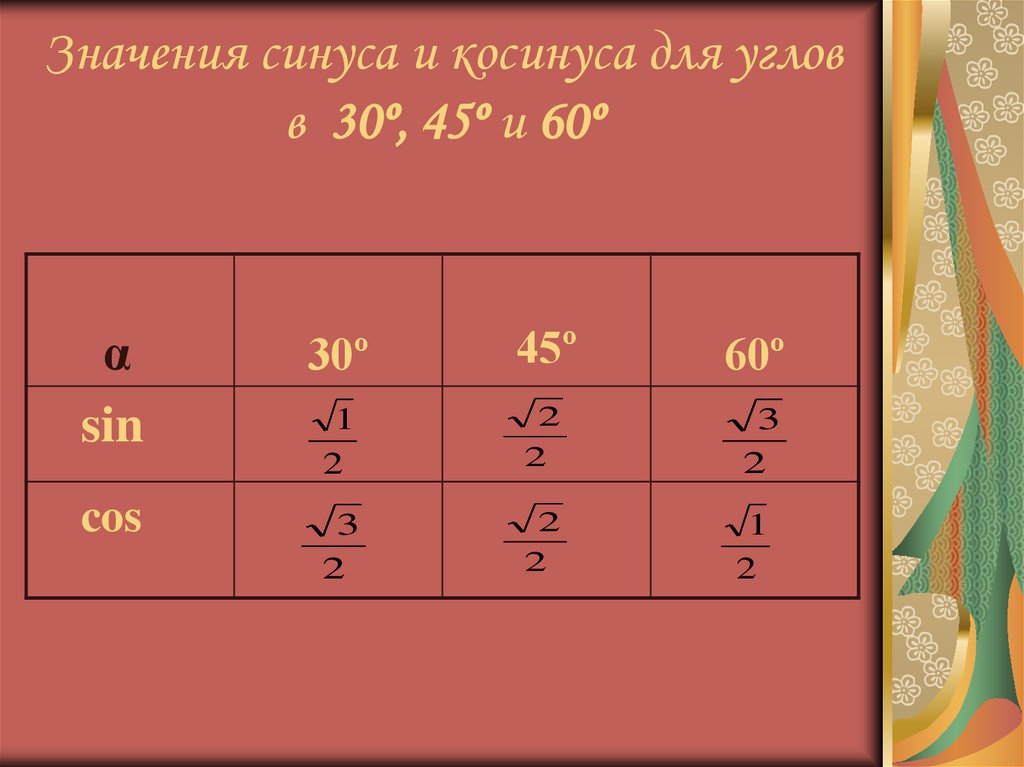
10. Значения синуса и косинуса для углов в 30º, 45º и 60º
αsin
30º
45º
60º
1
2
2
2
3
2
cos
3
2
2
2
1
2
11.
Чтобы указать значения тангенса икотангенса тех же углов достаточно
вспомнить ОТТ, т.е
sin
tg α =
,
cos
а котангенс взаимно обратная
функция для тангенса.
12. Формулы приведения:
-Жил рассеянный математик, и каждый разпреобразовывая тригонометрические
функции углов вида , , 32 , 2 ,
2
он спрашивал у своей лошади, жующей за
окном сено, надо менять функцию на
«кофункцию» или нет. А лошадь кивала
головой по той оси, которой принадлежала
точка , 3 или , 2 , соответствую 2
2
щая первому слагаемому аргумента.
у
2
3
2
2
х
13. Формулы приведения:
Математику оставалось лишь записыватьответ, указывая знак данной функции.
Например,
cos = sin α; sin = sin α;
2
3
= -tg α;
сtg
2
tg 2 = tg α.
Знаки тригонометрических функций:
cos α
у
у
+
-
+
-
х
-
+
-
+
tg α и сtg α
у
х
-
+
sin α
+
-
х
14. Формулы сложения:
Формулы сложения – это та группа формул, которуюнужно знать наизусть. Но для их запоминания можно
тоже воспользоваться ассоциативным приемом. У
косинуса функции одноименные:
cos ( α - β ) = cos α cos β + sin α sin β;
cos ( α + β ) = cos α cos β - sin α sin β;
а у синуса разноименные:
sin (α + β) = sin α cos β + cos α sin β;
sin (α - β) = sin α cos β - cos α sin β.
Не все в нашей жизни бывает «гладко»: за белой
полосой идет черная, и наоборот. Так и у наших
функций, если функции идут одноименные, то знаки
не совпадают, а если разноименные, то совпадают.
15. Формулы сложения:
Для получения формулы тангенса суммы итангенса разности достаточно применить
ОТТ и разделить числитель и знаменатель
полученной дроби на cos α cos β, где
cos α ≠ 0 и cos β ≠ 0.
tg tg
tg tg
tg (α + β) =
;
tg (α - β) =
1 tg tg
1 tg tg
Например,
сos 97º cos 67º + sin 97º sin 67º = сos (97º- 67º) =
= сos 30º =… ;
sin 25º сos 20º + cos 25º sin 20º = sin (25º + 20º)=
= sin 45º =… .
16. Формулы двойного угла:
Чтобы получить тригонометрическиеформулы двойного аргумента достаточно в
формулах сложения β заменить на α.
Например,
cos 2α = cos (α +α)= cos α cos α - sin α sinα =
= cos²α - sin²α;
sin 2α = sin (α + α) = sin α cos α + sin α cos α =
=2sin α cos α
tg tg
2tg
tg2α = tg (α + α ) =
1 tg tg 1 tg 2
Поэтому, 2 sin 65º cos 65º = sin (2∙ 65º) =
=sin130º = sin (180º - 50º) = sin 50º
17. Формулы суммы и разности тригонометрических функций
18.
19. Найдите значение выражения
20. Найдите значение выражения
21. Найдите значение выражения
22. Вычислите:
23. Вычислите:
075
1. sin
2. cos 150
3. cos 8400
24. Рефлексия
+ я могу сам применять формулы+ - затрудняюсь
- не умею применять формулы
















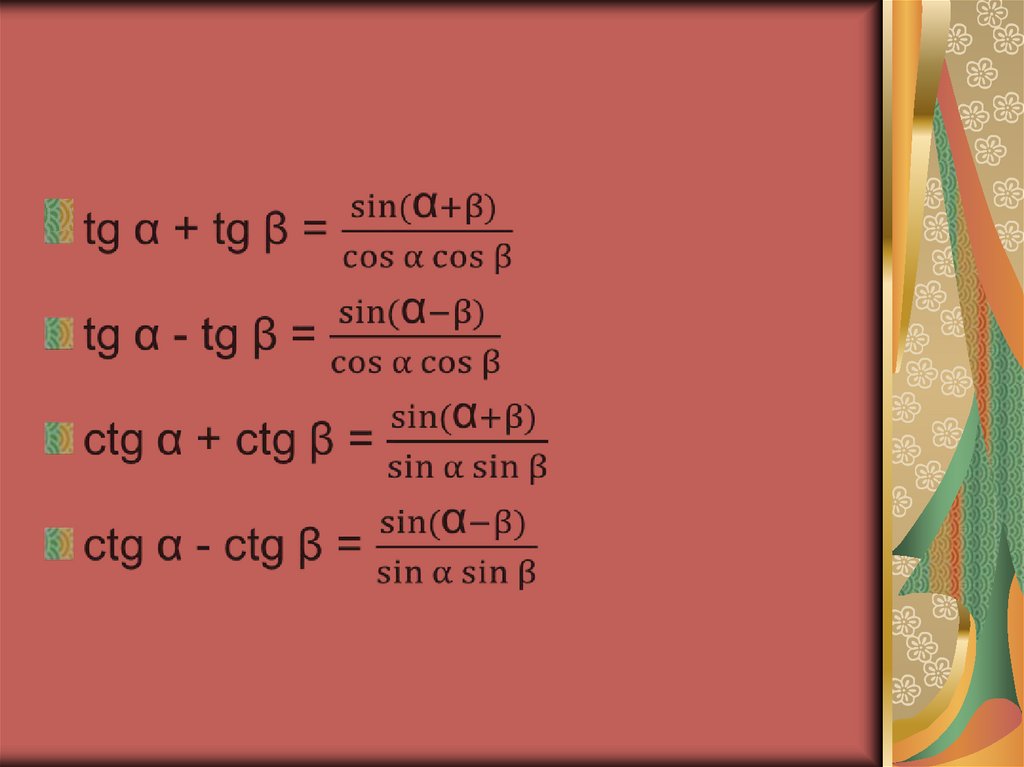






 Математика
Математика








