Похожие презентации:
Формулы тригонометрии
1.
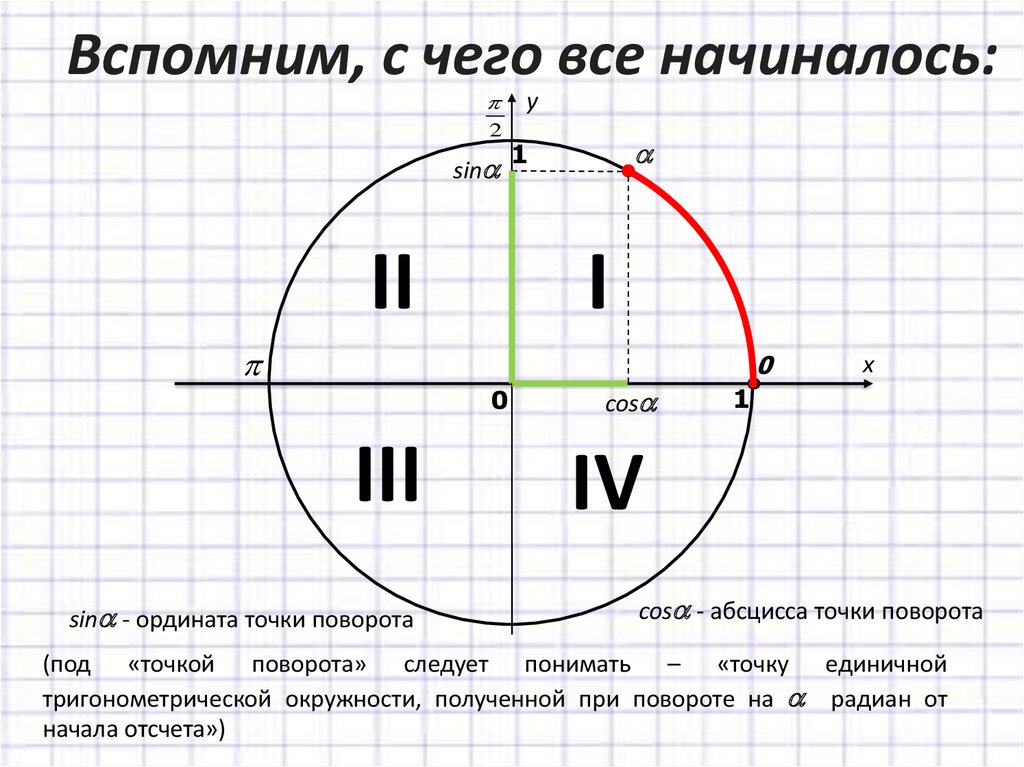
2. Вспомним, с чего все начиналось:
2sin
II
y
1
I
0
0
III
sin - ордината точки поворота
cos
x
1
IV
cos - абсцисса точки поворота
(под «точкой поворота» следует понимать – «точку единичной
тригонометрической окружности, полученной при повороте на радиан от
начала отсчета»)
3.
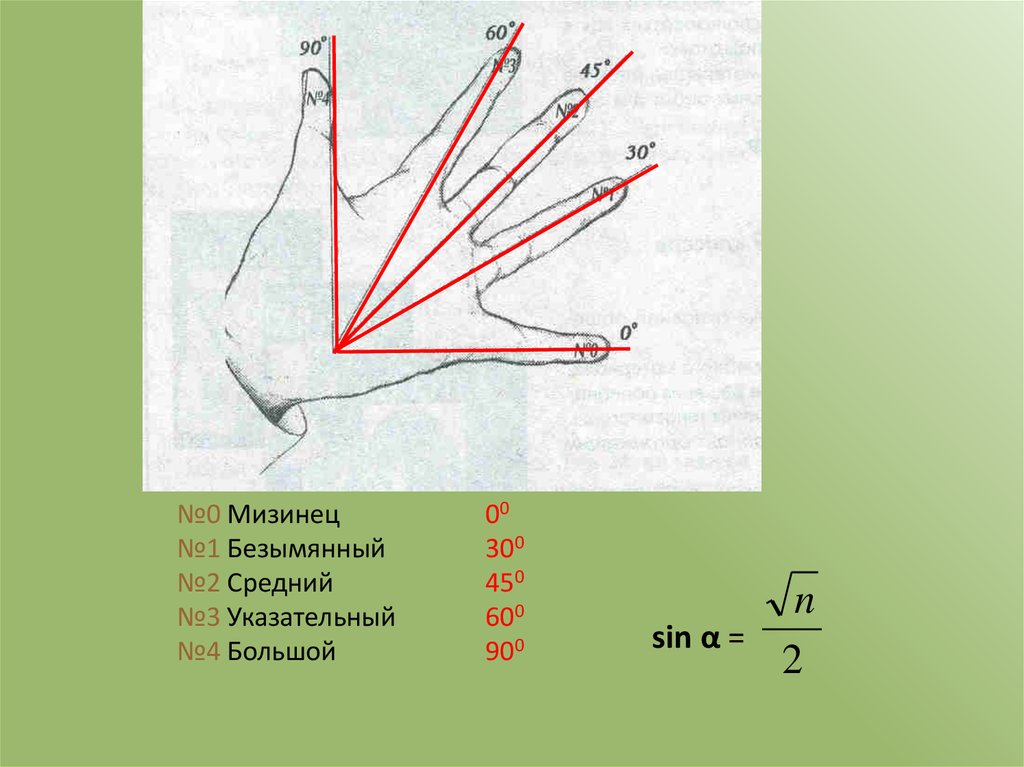
№0 Мизинец№1 Безымянный
№2 Средний
№3 Указательный
№4 Большой
00
300
450
600
900
n
sin α =
2
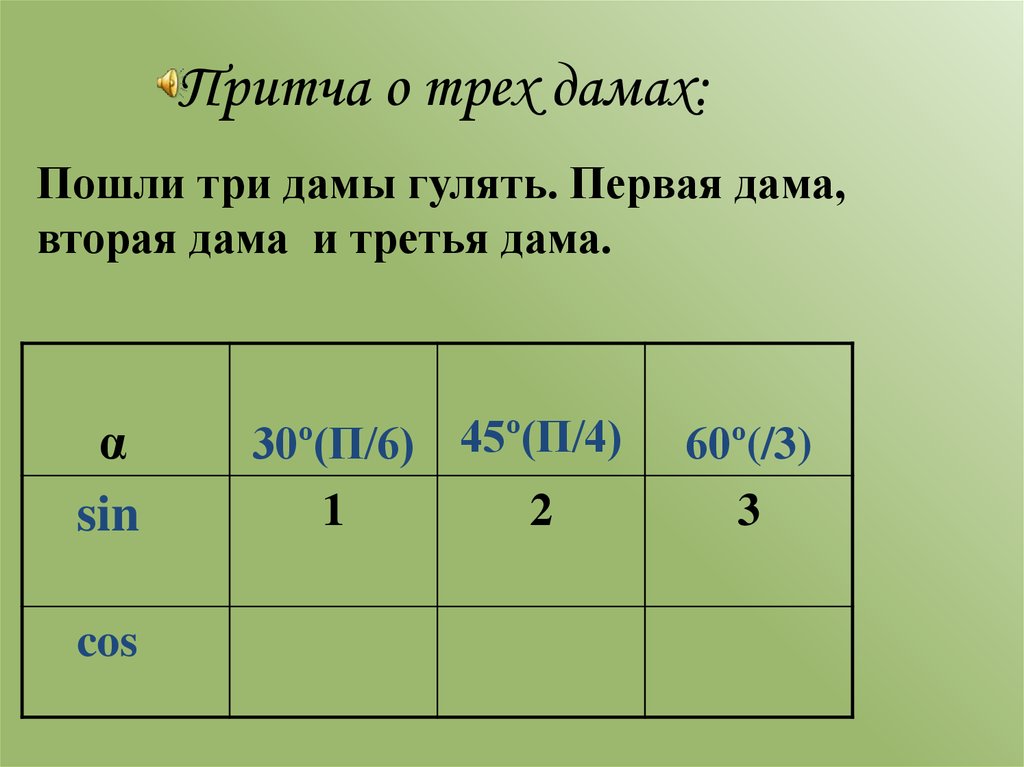
4. Притча о трех дамах:
Пошли три дамы гулять. Первая дама,вторая дама и третья дама.
α
sin
cos
30º(П/6) 45º(П/4)
1
2
60º(/3)
3
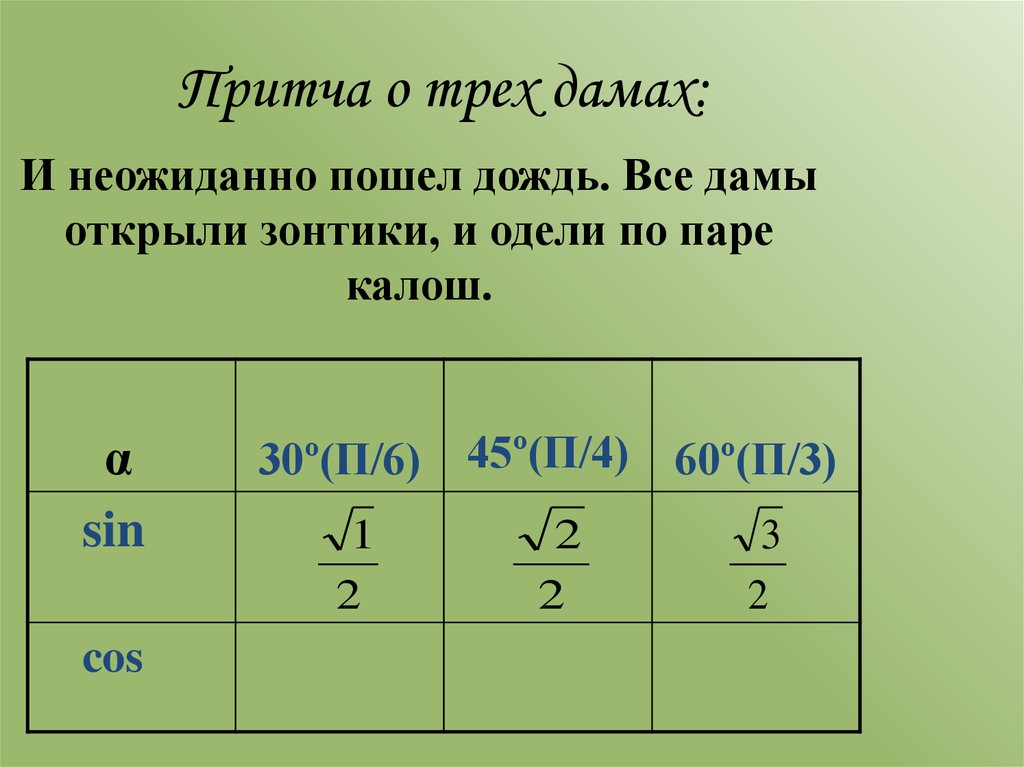
5. Притча о трех дамах:
И неожиданно пошел дождь. Все дамыоткрыли зонтики, и одели по паре
калош.
α
sin
cos
30º(П/6) 45º(П/4) 60º(П/3)
1
2
2
2
3
2
6. Притча о трех дамах:
Прогулка была закончена. Перваядама, вторая дама и третья дама
пошли домой.
α
30º(П/6) 45º(П/4) 60º(П/3)
sin
cos
3
2
2
2
1
2
7. Значения синуса и косинуса для углов в 30º, 45º и 60º (П/6; П/4; П/3)
αsin
cos
30º (П/6) 45º(П/4) 60º(П/3)
1
2
2
2
3
2
3
2
2
2
1
2
8. Знаки по четвертям: как запомнить?
Важно помнить, чтовсе тригонометрические функции в I четверти принимают положительные значения (знак
«+»);
у синуса знаки расположены горизонтально, у косинуса – вертикально, а
у тангенса и котангенса – крест-накрест.
правило: произносить слова «синус» и «косинус» нужно нараспев, выделяя ударную гласную и
фиксируя при этом, в каком направлении вытягивается рот. При произнесении слова «синус»
ударная гласная «и» вытягивает рот в направлении «↔», значит, у синуса знаки расположены
горизонтально. Аналогично, при произнесении слова «косинус», ударная гласная «о» вытягивает
рот в направлении «↕», значит, у косинуса знаки расположены вертикально.
9. Основное тригонометрическое тождество
10.
косинус квадраточень рад
К нему едет братсинус квадрат.
Когда встретятся они,
окружность удивится:
выйдет целая семья, то есть единица
11. Формулы приведения:
• В старые добрые времена жилрассеянный математик, и каждый раз
преобразовывая тригонометрические
функции углов вида 3 2
2
в поисках ответа
2
он спрашивал у своей умной лошади,
жующей за окном сено, надо менять
функцию на «кофункцию» или нет. А
лошадь кивала головой по той оси,
которой принадлежала точка , 3
или
,2 , соответствую 2 2
щая первому слагаемому аргумента.
12. Формулы приведения:
Математику оставалось лишь записыватьответ, указывая знак данной функции.
Например,
cos = sin α;
sin = sin α
2
3
= -tg α;
Сtg
2
tg 2 = tg α.
Знаки тригонометрических функций:
cos α
у
у
+
-
+
-
х
-
+
-
+
tg α и сtg α
у
х
-
+
sin α
+
-
х
13. Пример
y2
1
+
+
- α)= -cosα
x
0
0
I
1
I
sin(
14. Формулы сложения: как их лучше запомнить?
1. sin( ) sin cos cos sin2. sin( ) sin cos cos sin
3. cos( ) cos cos sin sin
4. cos( ) cos cos sin sin
tg tg
5.tg ( )
1 tg tg
tg tg
6.tg ( )
1 tg tg
чтобы не запутаться в знаках, надо запомнить простое
правило:
Синус сохраняет знак и перемешивает функции, а косинус
меняет знак и не перемешивает функции
15. Формулы двойного угла
1. sin2α=2sinαcosαsin(α+α)=sinαcosα+
2
2
sinαcosα
2.cos2α cos α sin α
2tgα
3.tg2 α
2
1 tg α
16. Продолжение следует…
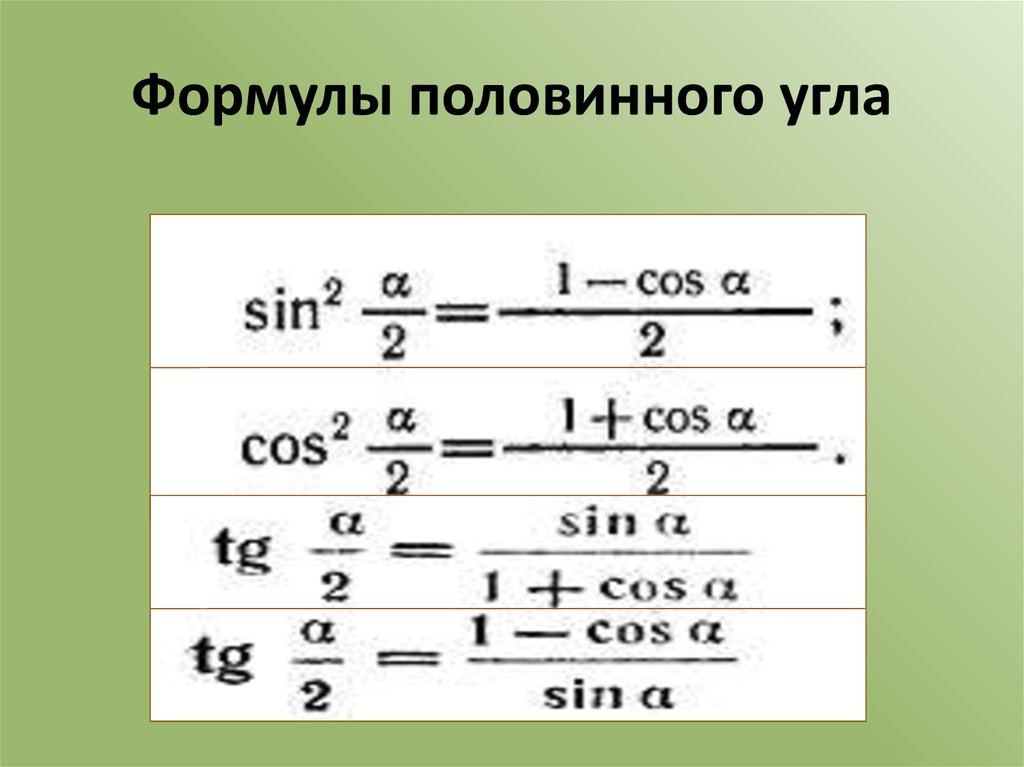
17. Формулы половинного угла
18. Очень важные следствия из этих формул…
1- cos2α=2sin²α1+cos2α=2cos²α
…и
Формулы понижения степени
cos²α = 1+cos2α/2
sin²α = 1- cos2α/2
Важно понять структуру этих формул, в частности, такой
момент – «степень понижается, а угол становится в два
раза больше». Эти формулы очень похожи друг на друга,
поэтому для лучшего их запоминания следует применять
правило: «Единица минус – дает синус, а единица плюс – дает
косину́с».
19. Формулы суммы и разности
1. sin sin 2 sincos
2
2
2. sin sin 2 sin
cos
2
2
3. cos cos 2 cos
cos
2
2
4. cos cos 2 sin
sin
2
2
sin( )
5.tg tg
cos cos
sin( )
6.ctg ctg
sin sin
20. Итоговое тестирование:
1. Укажите значение выражения cos 60ºA)
3
;
2
1
C)
;
2
B) 1;
2. Упростите выражение cos
D) 0.
А) cos α ; B) sin α ; C) - cos α ; D) - sin α .
3. Найдите значение выражения
sin 57º cos 27º + сos 57º sin 27º
3
1
A)
; B) 1;
C) 0 ;
D)
.
2
2
4. Упростите выражение 2 sin 75º cos 75º
1
3
A) 0;
B) 1;
C)
;
D)
.
2
2
5.Представьте в виде произведения sin 80º + sin 40º
A) 3 sin 20º;B) - 3 cos 20º;C) 3 cos20º; D) - sin 20º .















 Математика
Математика