Похожие презентации:
Формулы приведения. Основные тригонометрические тождества
1.
Формулы приведения. Основныетригонометрические тождества
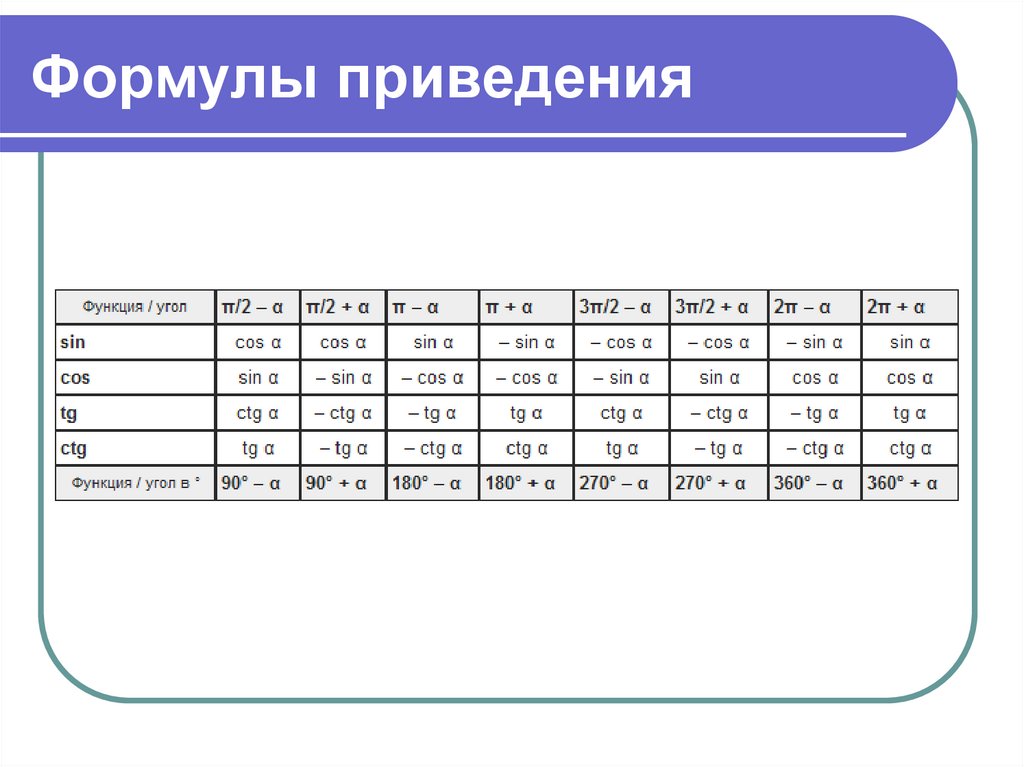
2. Формулы приведения
Формулы приведения позволяют перейти оттригонометрической функции углов
вида 90∘±α, 180∘±α, 270∘±α или 360∘±α к
тригонометрической функции элементарного
угла α.
Например, формулами приведения являются
такие распространенные формулы:
cos(90∘−α)=sinα, sin(90∘−α)=cosα.
Угол альфа лежит пределах от 0 до 90 градусов
3. Формулы приведения
4. Правило для запоминания формул приведения
1. Определите знак функции в соответствующей четверти.Напомним их:
2.Если в формуле содержатся углы 180∘ или 360∘, то наименование
функции не изменяется. Если же в формуле содержатся
углы 90∘ или 270∘, то функция изменяется на ко-функцию (т.е.,
синус на косинус, тангенс на котангенс и наоборот).
5. Пример применения формул приведения
Вычислить sin 150 , cos 120Решение :
1
sin 150 sin( 180 30 ) sin 30
2
1
cos 120 cos(90 30 ) sin 30
2
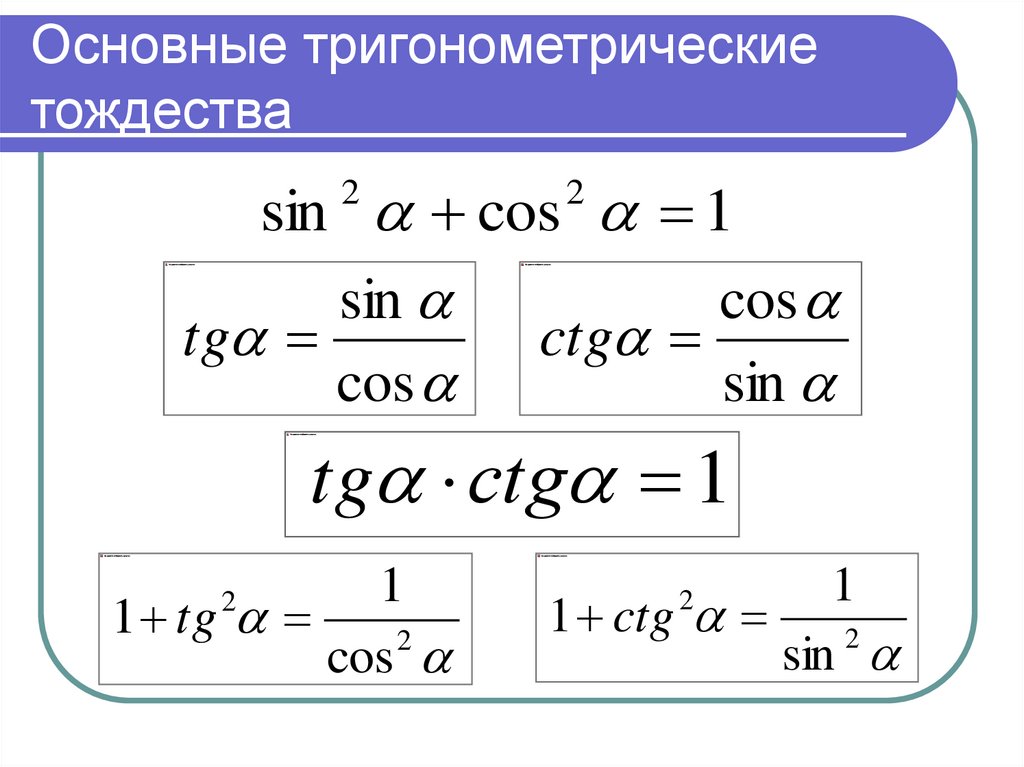
6. Основные тригонометрические тождества
Равенство, справедливое при всех допустимыхзначениях аргументов, называется тождеством.
Если в состав входят тригонометрические функции
(синус, косинус, тангенс или котангенс), то тождество
называется тригонометрическим.
7. Основные тригонометрические тождества
sin cos 1sin
cos
tg
ctg
cos
sin
2
2
tg сtg 1
1
1 tg
2
cos
2
1
1 ctg
2
sin
2
8. Основное тригонометрическое тождество
sin 2 cos 2 1Эта формула связывает синус и косинус одного угла. Теперь, зная
синус, мы легко найдем косинус — и наоборот. Достаточно извлечь
квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что
из основного тригонометрического тождества непонятно, каким
был исходный синус и косинус: положительным или
отрицательным. Ведь возведение в квадрат — четная функция,
которая «сжигает» все минусы (если они были).
Именно поэтому во всех задачах есть дополнительные условия,
которые помогают избавиться от неопределенности со знаками.
Обычно это указание на координатную четверть, по которой можно
определить знак
9. Примеры применения основного тригонометрического тождества
Пример 1.Пример 2.
10. Тригонометрические формулы двойного аргумента (двойного угла)
11. Пример применения формулы двойного аргумента
Упростите выражениеcos x sin x cos x sin x cos x sin x
cos 2 x
cos 2 x sin 2 x
2
1 sin 2 x cos x sin 2 x 2 sin x cos x
cos x sin x
cos x sin x 2
12. Тригонометрические формулы половинного угла
x 1 cos xx
1 cos x
sin
sin
2
2
2
2
2
x 1 cos x
x
1 cos x
cos
cos
2
2
2
2
2










 Математика
Математика








