Совместимые и не совместимые понятия

1.

СОВМЕСТИМЫЕ И
НЕСОВМЕСТИМЫЕ
ПОНЯТИЯ.

2.

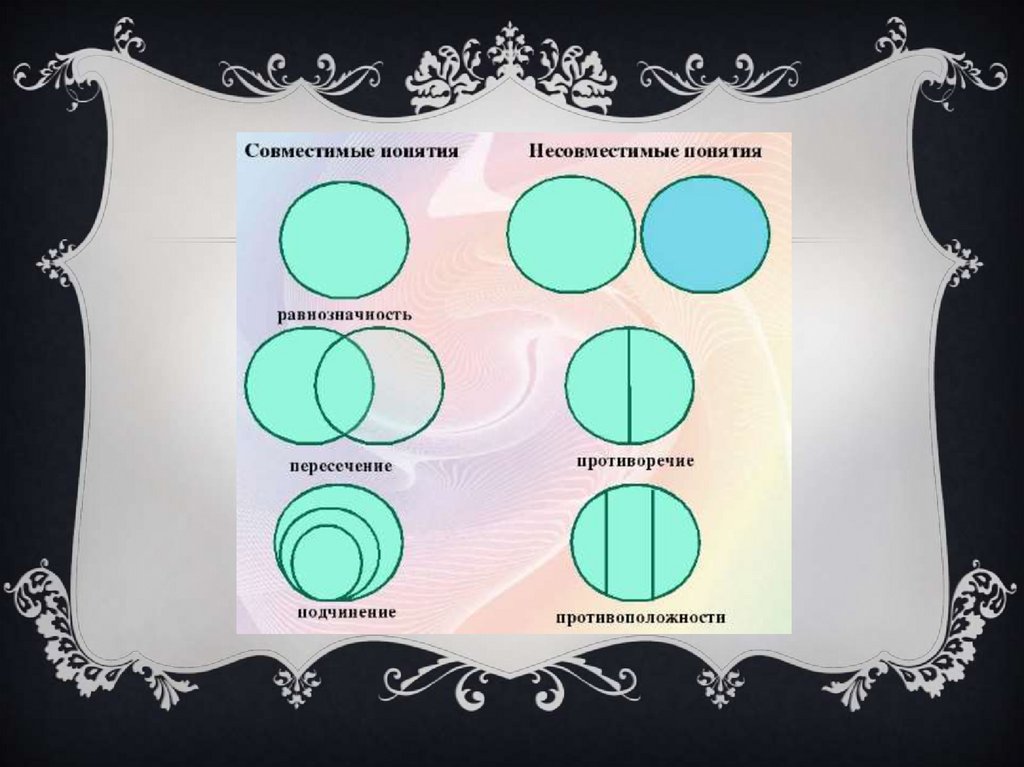
СОВМЕСТИМЫЕ ПОНЯТИЯ
1. Отношения равнозначности
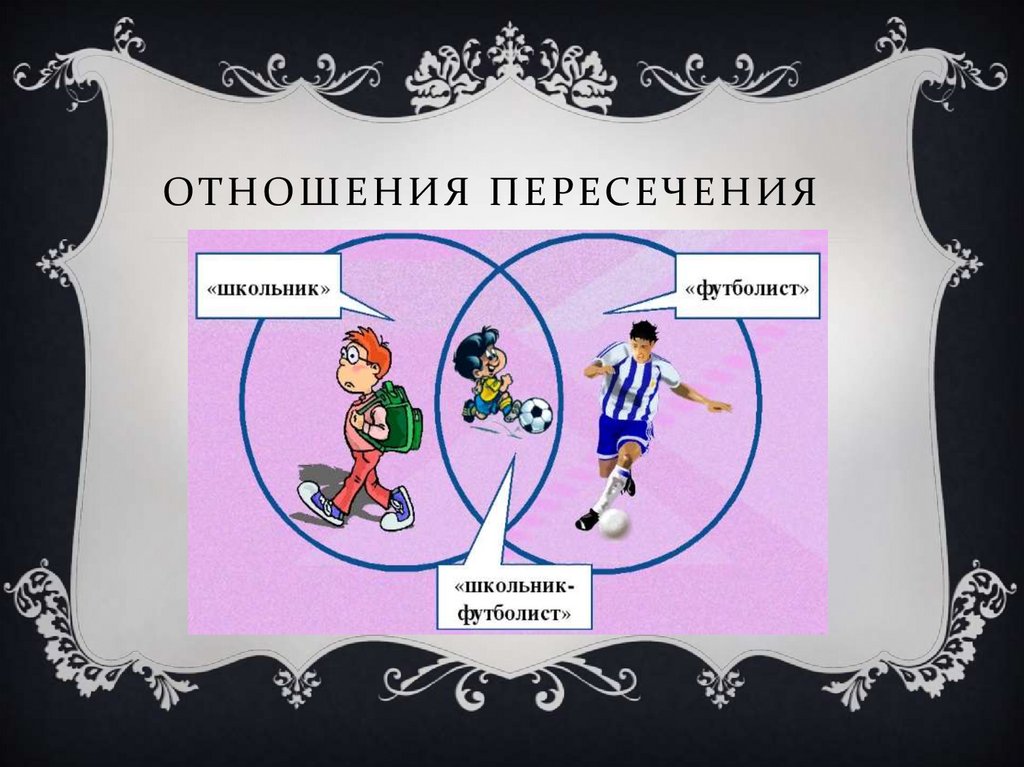
2. Отношения пересечения
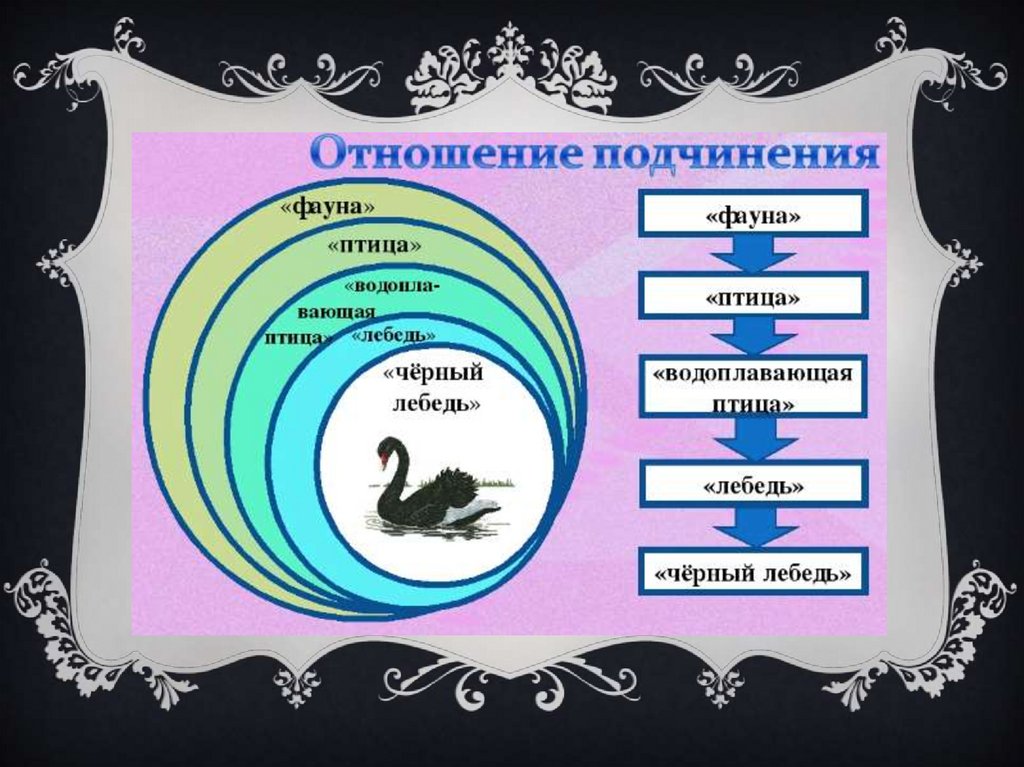
3. Отношения подчинения

3.

ОТ Н О Ш Е Н И Я
РА В Н ОЗ Н АЧ Н О С Т И

4.

Равнозначными
ин
объект.
В
равнозначные
Отношения
пересекающиеся
Рассмотрим
на
,т«футболист».
«школьник»
признак,
однозначно
помогает
множества
-э
понятия
ся
буквой
н
школьников
футболистов,
Есть
которые
о
Ф
«
футбол
–
о
то
е
бозначим
енна
»есть
впримере
ии«человек,
школе,
тот
люди,
нарисуем
круги,
«Ш»
тот
На
или
же
«футболист»:
играют
который
диаграмме
их
существенный
других,
которые
но
пересечения
выделить
понятий
и
некоторые
изображающие
нарисуем
который
на
которые
Содержание
понятия,
всоответствующий
вназывают
футбол
диаграмме
понятия
футбол,
учат
«школьник»
обозначаемый
Эйлера
«человек,
учится
были,
футболисты
совпадают,
круг,
нено
понятия,
понятия
играют.
условно
есть
вв школе
школе».
который
икруг.
иОбозначим
то
которые
будут.
учатся
объект
отражающий
не
Некоторые
есть
Содержание
учатся
играет
визображаются
отражают
из
школе
ихвшкольники
футбол».
на диаграмме
од одним
играют
кругом.
всех
в
Равнозначными называют понятия,
которые отражают один и тот же объект. На
диаграмме Эйлера –Венна круги,
изображающие равнозначные понятия,
совпадают, то есть изображаются одним
кругом.

5.

ОТ Н О Ш Е Н И Я П Е РЕС ЕЧ Е Н И Я

6.

7.

Пересекающиеся понятия на диаграмме
Эйлера-Венна изображаются
пересекающимися кругами, что означает,
что есть объекты, равно принадлежащие и
к одному, и к другому множеству объектов.

8.

9.

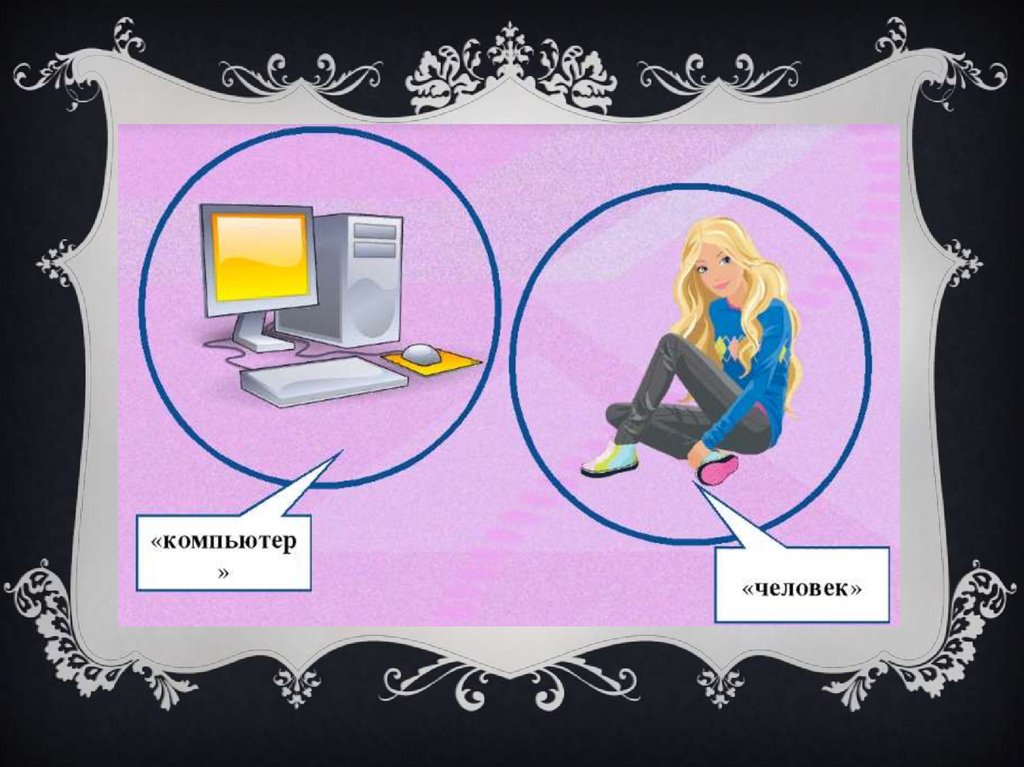
Н ЕСО В М ЕС Т И М Ы Е П О Н Я Т И Я
К несовместимым понятиям
относятся понятия, которые
отражают множества, где ни один
объект одного множества не является
элементом другого множества.

10.

11.

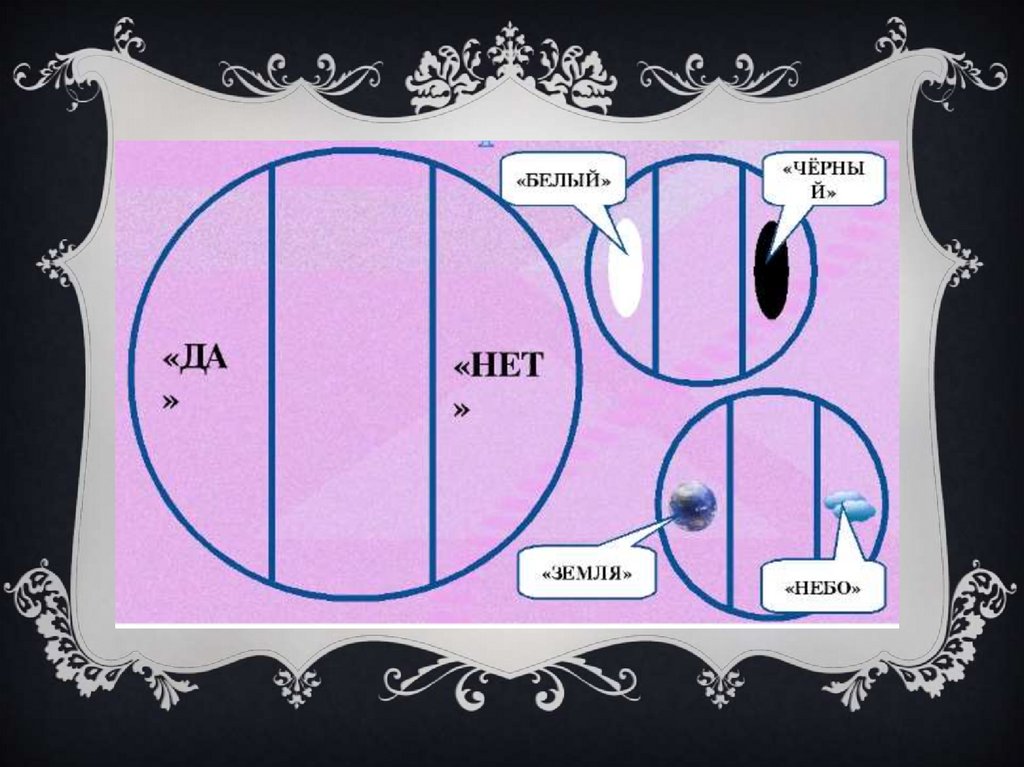
Круги Эйлера-Венна, обозначающие
несовместимые понятия, не пересекаются,
так как объекты этих понятий не имеют
общих объектов. Таким образом,
несовместимые понятия –это такие, в
объемах которых нет ни одного общего
элемента.