Теорема Пифагора

1.

Учитель математики Горкина Г.А.

2.

3.

I. Организационный момент
II. Актуализация знаний учащихся
Несколько слов о прямоугольных
треугольниках
Решение задач по готовым чертежам с целью
подготовки учащихся к восприятию нового
материала

4.

ПРЯМОУГОЛЬНЫЕ
ТРЕУГОЛЬНИКИ
Д АТ Ь О П Р Е Д Е Л Е Н И Е П РЯ М ОУ Г ОЛ Ь Н О Г О
Т Р Е У Г ОЛ Ь Н И К А
О П Р Е Д Е Л Е Н И Е К АТ Е Т О В И Г И П О Т Е Н У З Ы
П Р И З Н А К И РА В Е Н С Т ВА
П РЯ М ОУ Г ОЛ Ь Н Ы Х Т Р Е У Г ОЛ Ь Н И КО В
Ф О РМ УЛ А Н А ХОЖ Д Е Н И Я П Л О Щ А Д И
П РЯ М ОУ Г ОЛ Ь Н О Г О Т Р Е У Г ОЛ Ь Н И К А

5.

С
В
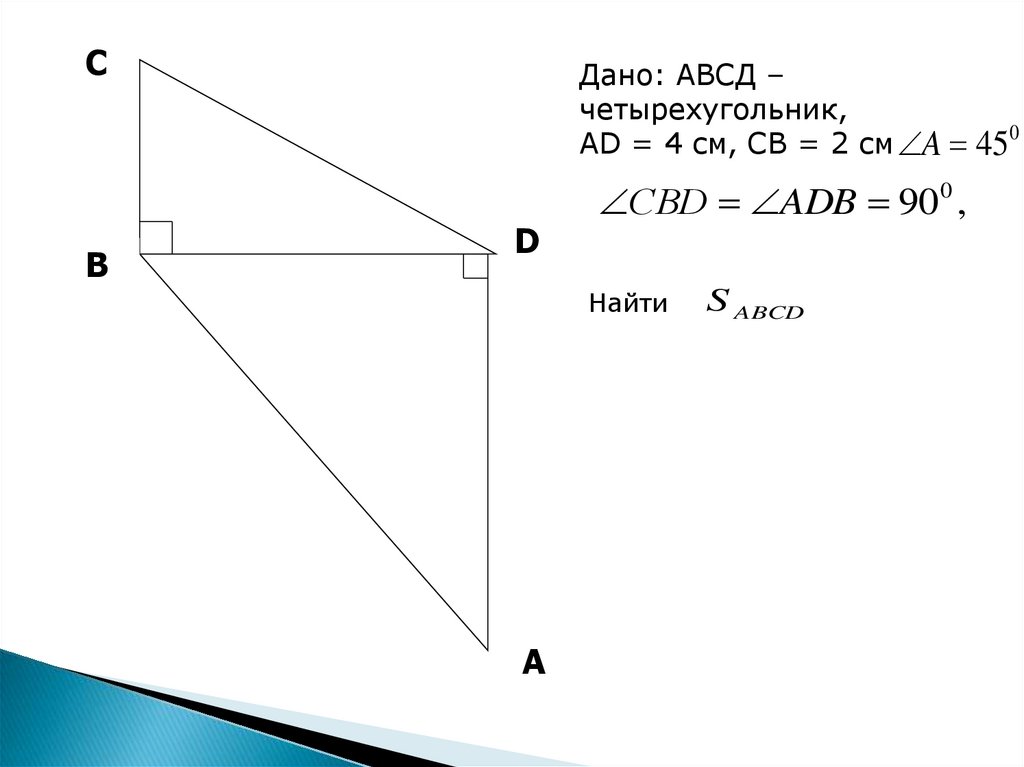
Дано: АВСД –
четырехугольник,
0
AD = 4 см, СВ = 2 см A 45
D
СВD ADB 90 0 ,
Найти
А
S ABCD

6.

С
В
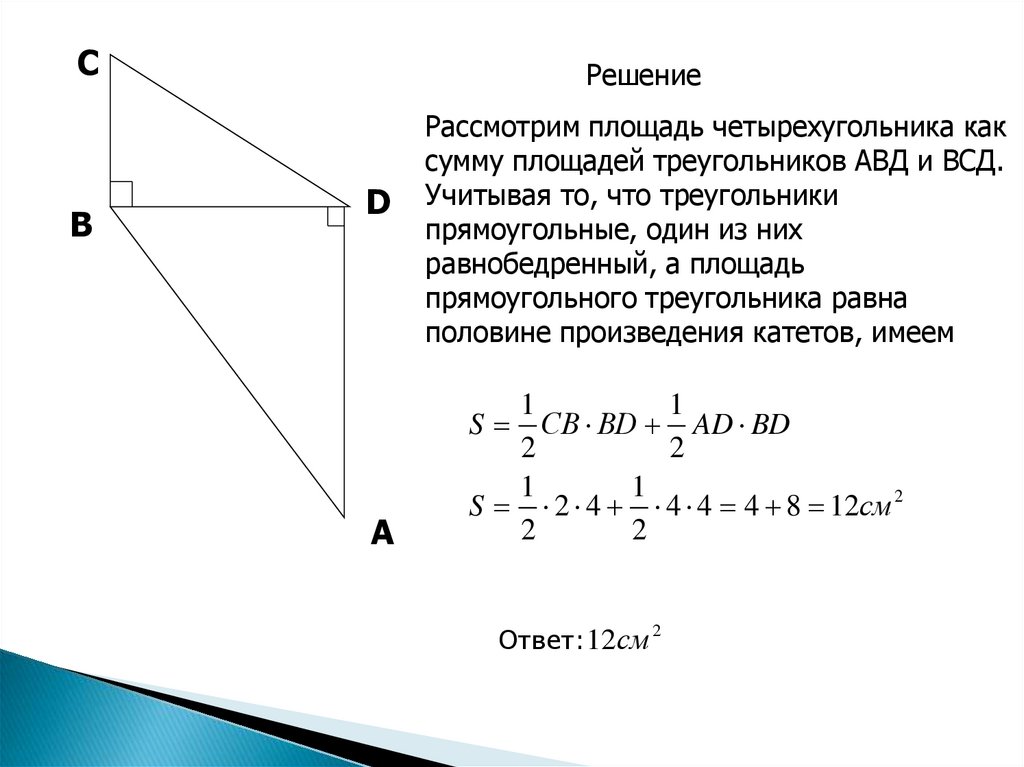
Решение
D
А
Рассмотрим площадь четырехугольника как
сумму площадей треугольников АВД и ВСД.
Учитывая то, что треугольники
прямоугольные, один из них
равнобедренный, а площадь
прямоугольного треугольника равна
половине произведения катетов, имеем
1
1
S СВ ВD AD BD
2
2
1
1
S 2 4 4 4 4 8 12см 2
2
2
Ответ:12см
2

7.

Теорема Пифагора
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов

8.

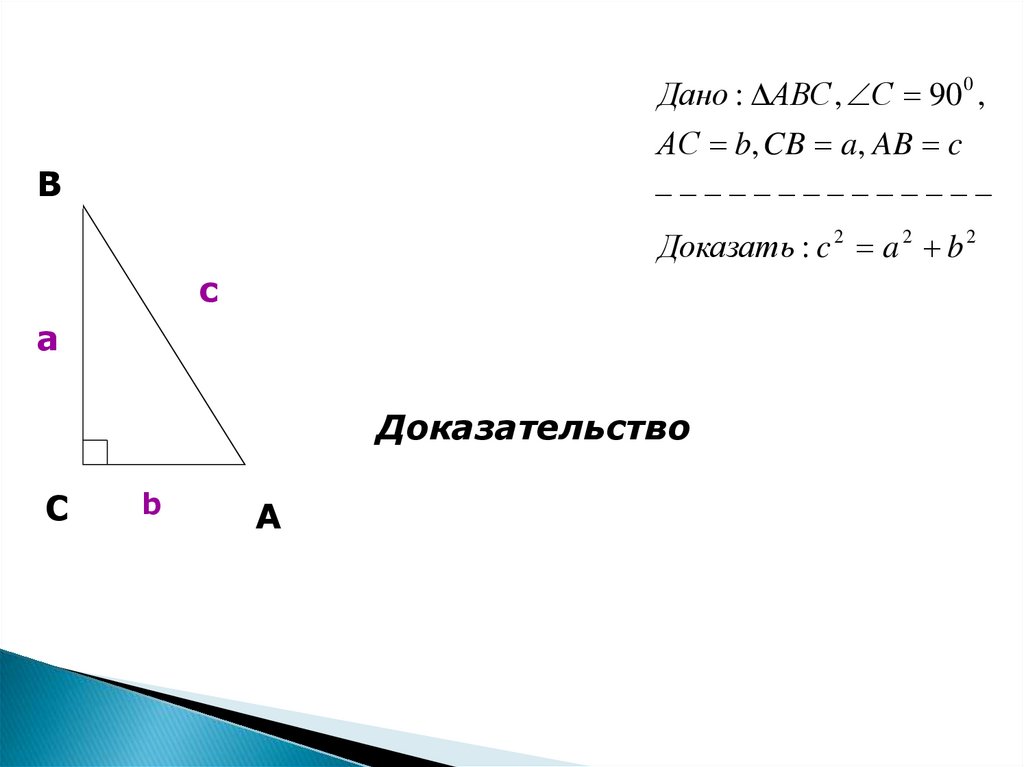
Дано : АВС , С 90 0 ,
АС b, CB a, AB c
В
Доказать : c 2 a 2 b 2
c
a
Доказательство
С
b
А

9.

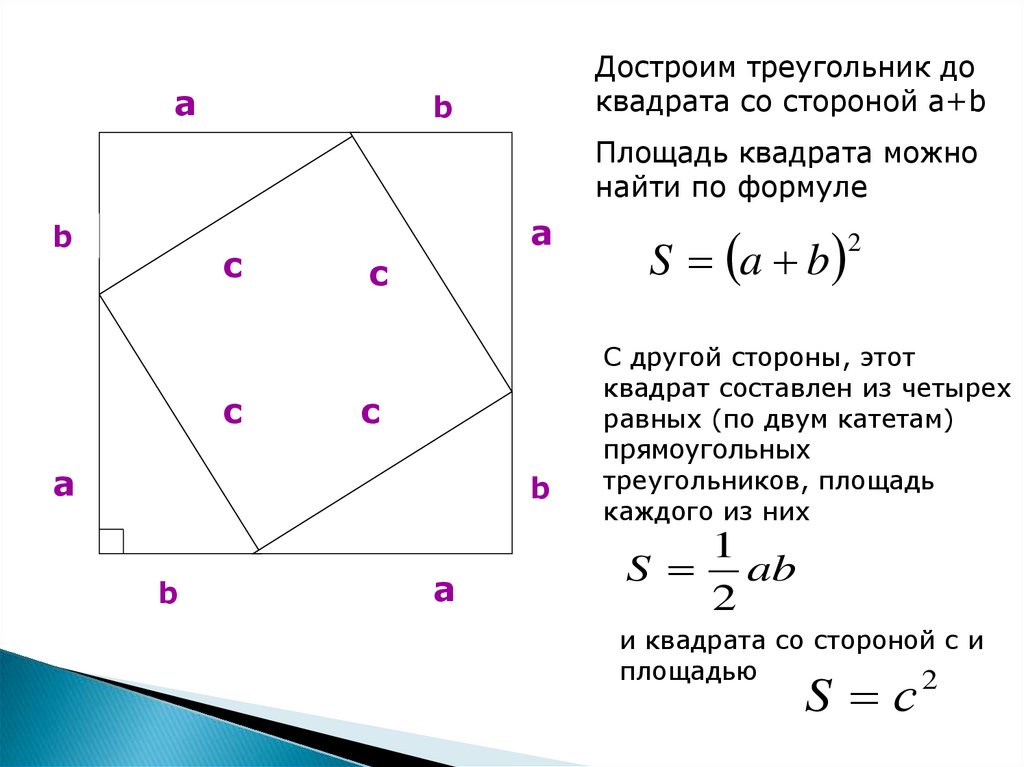
a
Достроим треугольник до
квадрата со стороной a+b
b
Площадь квадрата можно
найти по формуле
b
c
c
a
c
c
a
b
b
a
S a b
2
С другой стороны, этот
квадрат составлен из четырех
равных (по двум катетам)
прямоугольных
треугольников, площадь
каждого из них
1
S ab
2
и квадрата со стороной с и
площадью
2
S с

10.

имеем
Таким образом
a
b
1
(a b) 4( ab) c 2
2
2
a 2ab b 2ab c
2
b
c
c
2
a b c
2
c
c
2
Теорема доказана
a
b
a
2
2

11.

Найти ВС
В
6 см
С
А
8 см
ВС АС 2 АВ 2
ВС 82 62 64 36 100 10см
Ответ: ВС=10 см

12.

В
С
5 см
А
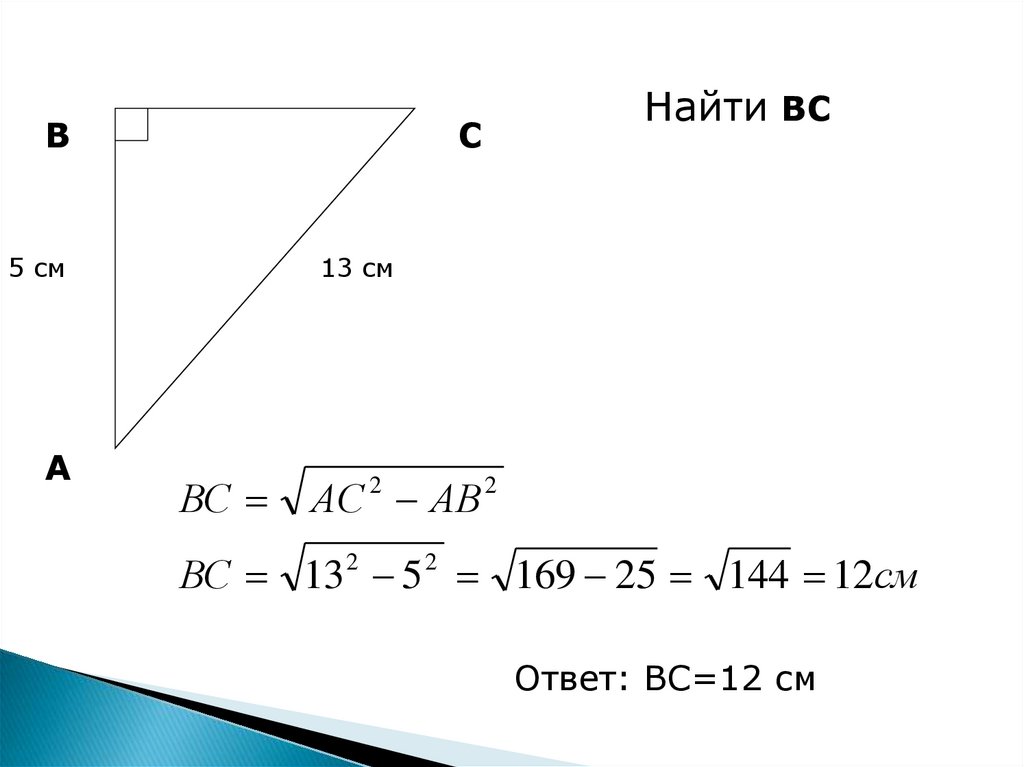
Найти ВС
13 см
ВС
АС 2 АВ 2
ВС 13 2 5 2 169 25 144 12см
Ответ: ВС=12 см

13.

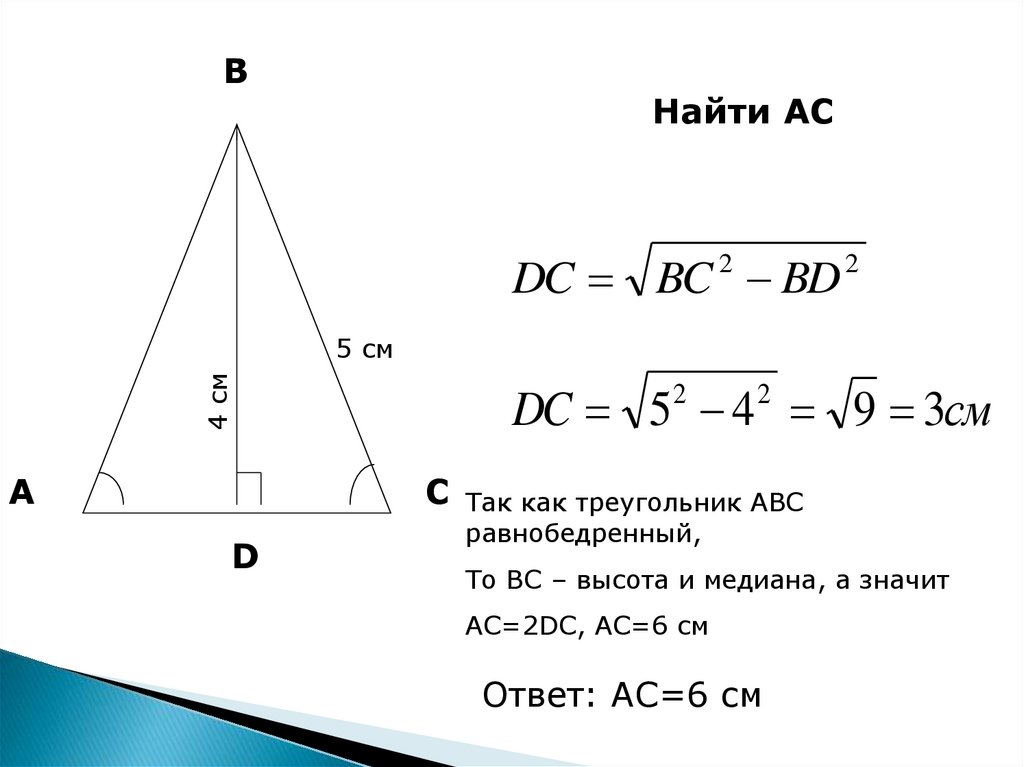
В
Найти AС
DC BC BD
2
2
4 см
5 см
А
DC 5 4 9 3см
2
С
D
2
Так как треугольник АВС
равнобедренный,
То ВС – высота и медиана, а значит
АС=2DC, АС=6 см
Ответ: АС=6 см

14.

Основания равнобедренной трапеции
равны 20 см и 30 см, боковые стороны – 13
см. Найти площадь трапеции.
Сторона квадрата равна а см. Найти длину
диагонали.
Диагонали ромба равны 14 см и 48 см.
Найдите сторону ромба.

15.

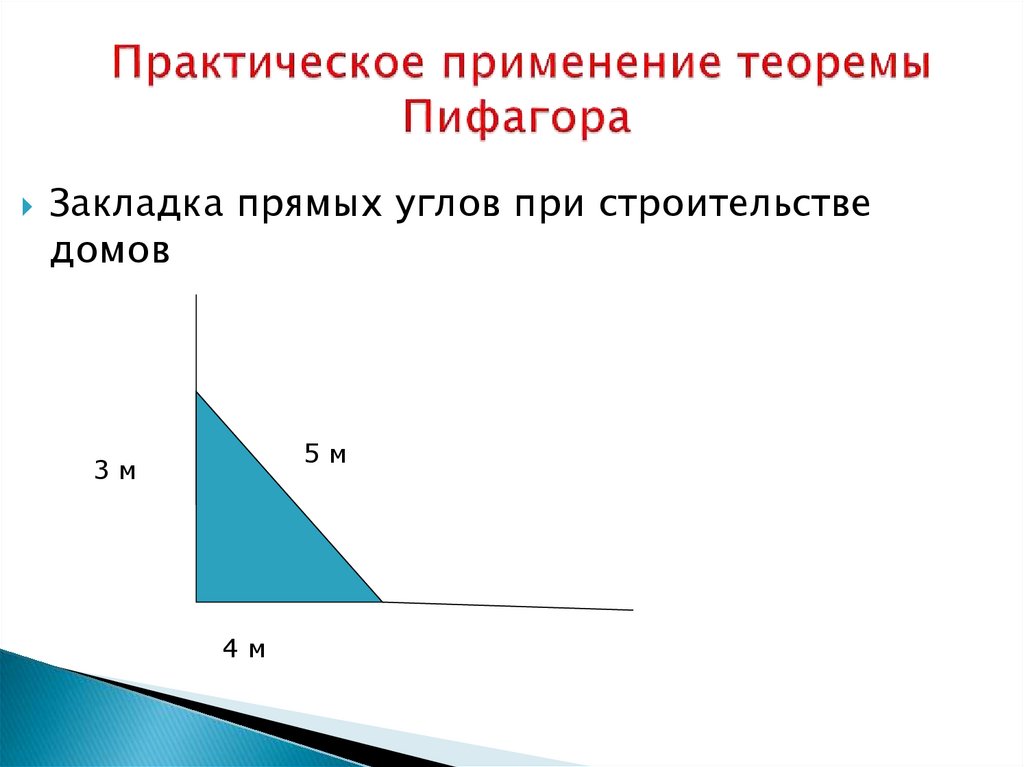
Закладка прямых углов при строительстве
домов
5м
3м
4м