Теорема обратная теореме Пифагора

1.

2.

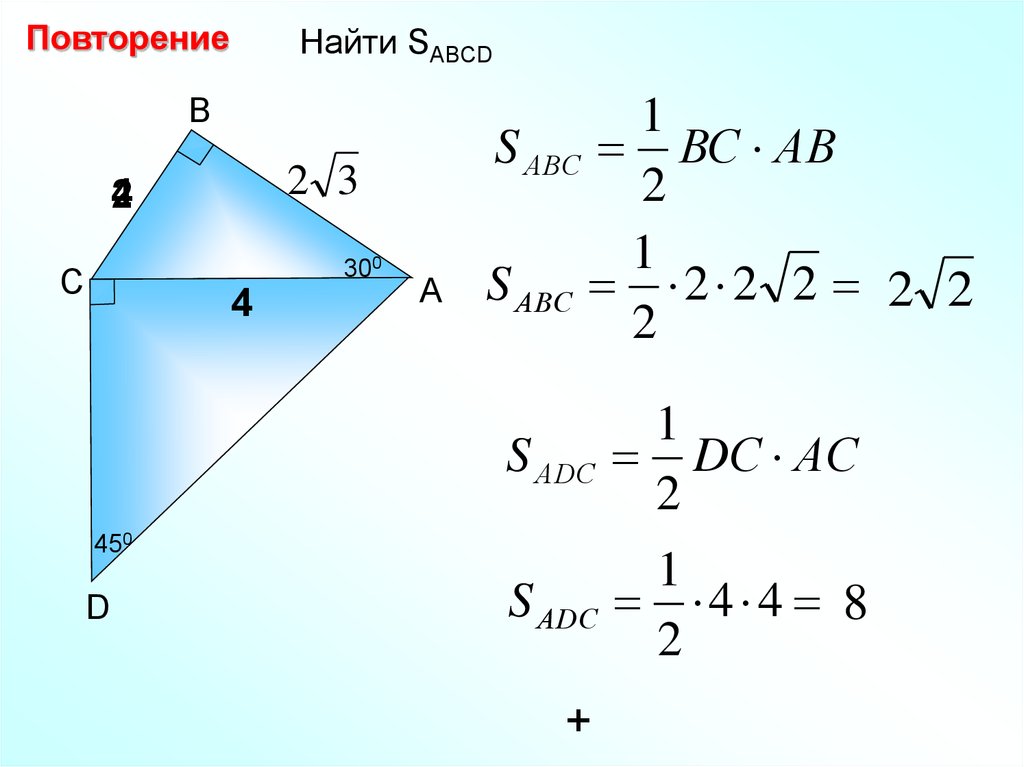
Повторение
Найти SABCD
В
2 3
4
2
300
С
4
А
1
S АВС ВС АВ
2
1
S АВС 2 2 2 2 2
2
S АDС
1
DС АC
2
S АDС
1
4 4 8
2
450
D
+

3.

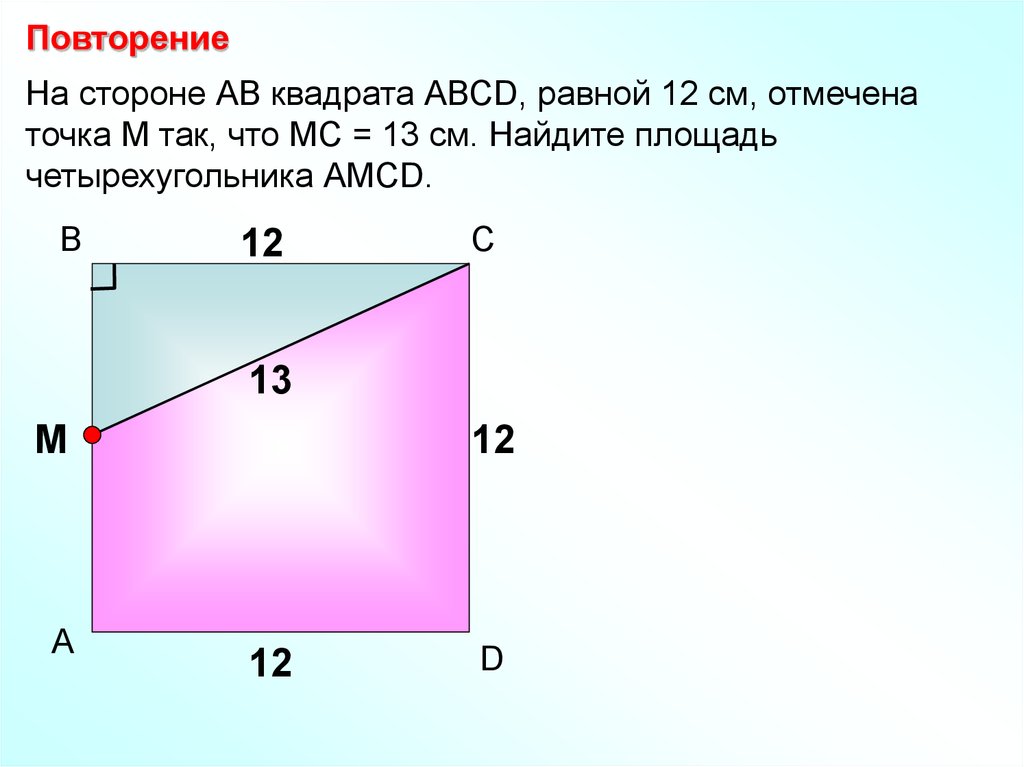
Повторение
На стороне АВ квадрата АВСD, равной 12 см, отмечена
точка М так, что МС = 13 см. Найдите площадь
четырехугольника АМСD.
В
12
С
13
М
А
12
12
D

4.

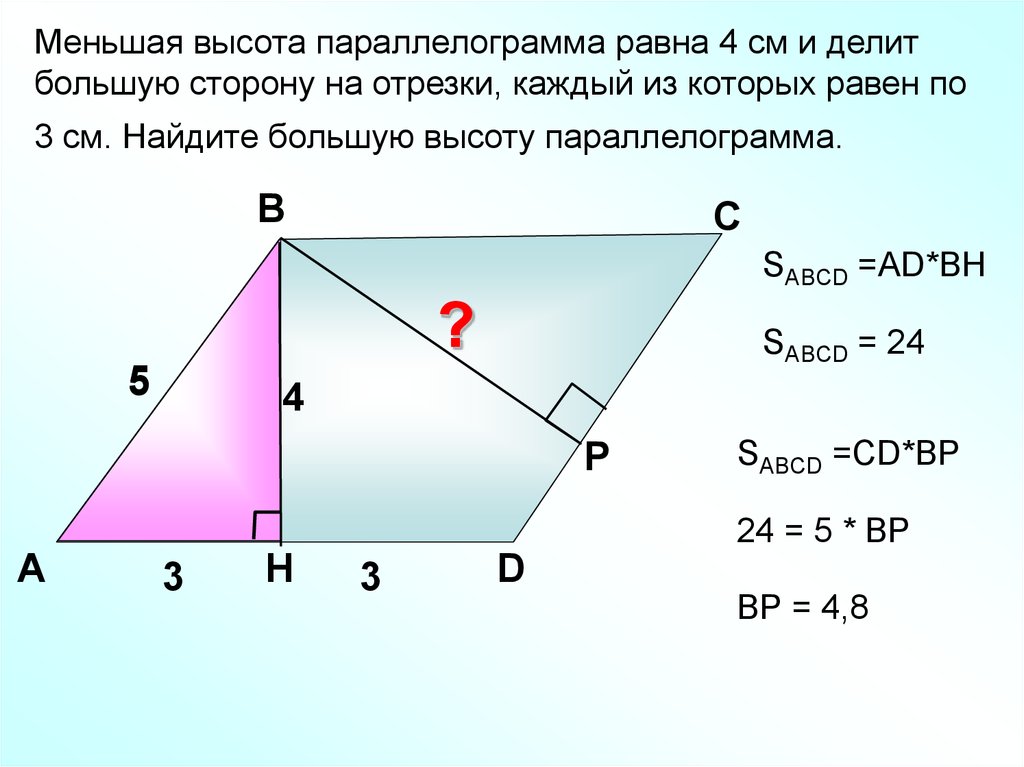
Меньшая высота параллелограмма равна 4 см и делит
большую сторону на отрезки, каждый из которых равен по
3 см. Найдите большую высоту параллелограмма.
В
С
SABCD =AD*BH
?
5
SABCD = 24
4
Р
А
SABCD =СD*BР
24 = 5 * ВР
3
H
3
D
ВР = 4,8

5.

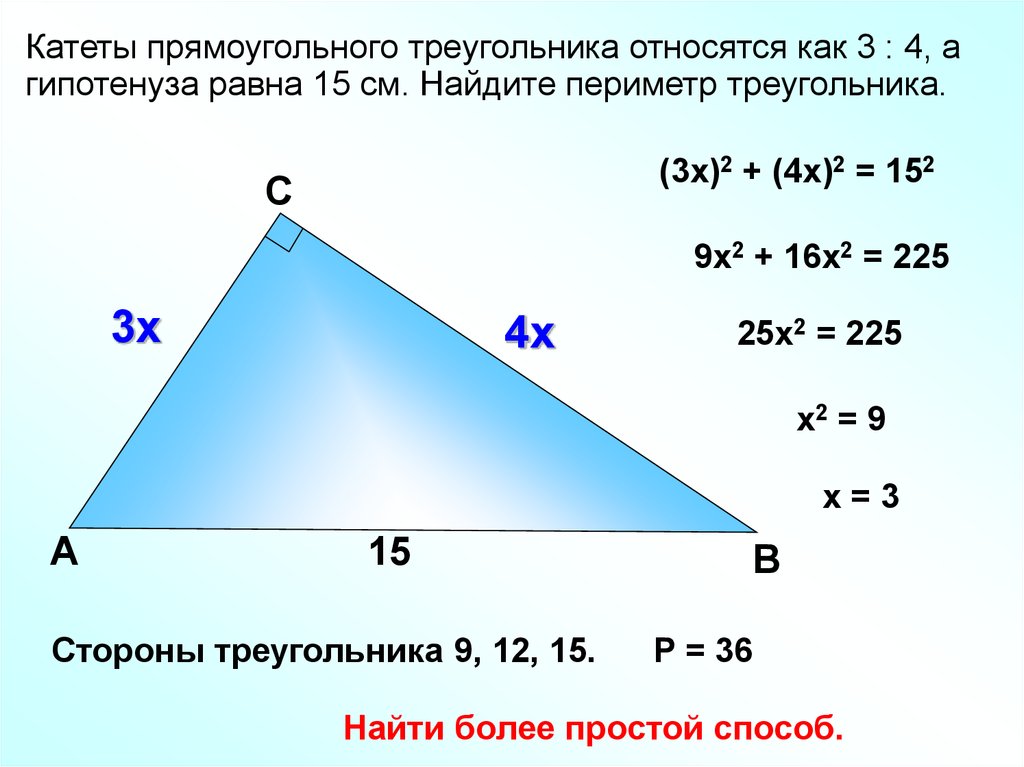
Катеты прямоугольного треугольника относятся как 3 : 4, а
гипотенуза равна 15 см. Найдите периметр треугольника.
(3х)2 + (4х)2 = 152
С
9х2 + 16х2 = 225
3х
4х
25х2 = 225
х2 = 9
х=3
A
15
Стороны треугольника 9, 12, 15.
В
Р = 36
Найти более простой способ.

6.

Построение прямого угла на местности
Для построения прямоугольной площадки для игры в футбол
следовало бы взять угольник и циркуль таких размеров.

7.

В
С древних времен известен очень
простой способ построения прямых углов
на местности.

8.

В
Этот способ применялся тысячелетия
назад строителями египетских
пирамид.

9.

Теорема, обратная теореме Пифагора.
Если квадрат одной стороны треугольника равен
сумме квадратов двух других сторон, то треугольник
прямоугольный.
Существует бесчисленное множество целых
положительных чисел, удовлетворяющих соотношению
с2 = а2 + b2.
Они называются п и ф а г о р о в ы м и
числами

10.

Вот несколько троек пифагоровых чисел.
32 + 42 = 52
62 + 82 = 102
52 + 122 = 132
72 + 242 = 252
92 + 402 = 412
112 + 602 = 612
132 + 842 = 852
92 + 122 = 152
122 + 162 = 202
Треугольник со сторонами 3, 4 и 5 часто
называют египетским треугольником
т. к. он был известен еще древним
египтянам.

11.

Катеты прямоугольного треугольника относятся как 3 : 4, а
гипотенуза равна 15 см. Найдите периметр треугольника.
С
5х = 15
х=3
3х
A
4х
15
5х
В

12.

Блиц-опрос
Определить углы треугольника со сторонами 1,
2 – большая сторона
2
2
3 1
2
3, 2
900
3
1
2
300
600
2
Треугольник – прямоугольный,
гипотенуза
2,
катеты 1 и
Углы треугольника 900, 600, 300, т.к. катет, равный 1, в два
раза больше гипотенузы 2.
3

13.

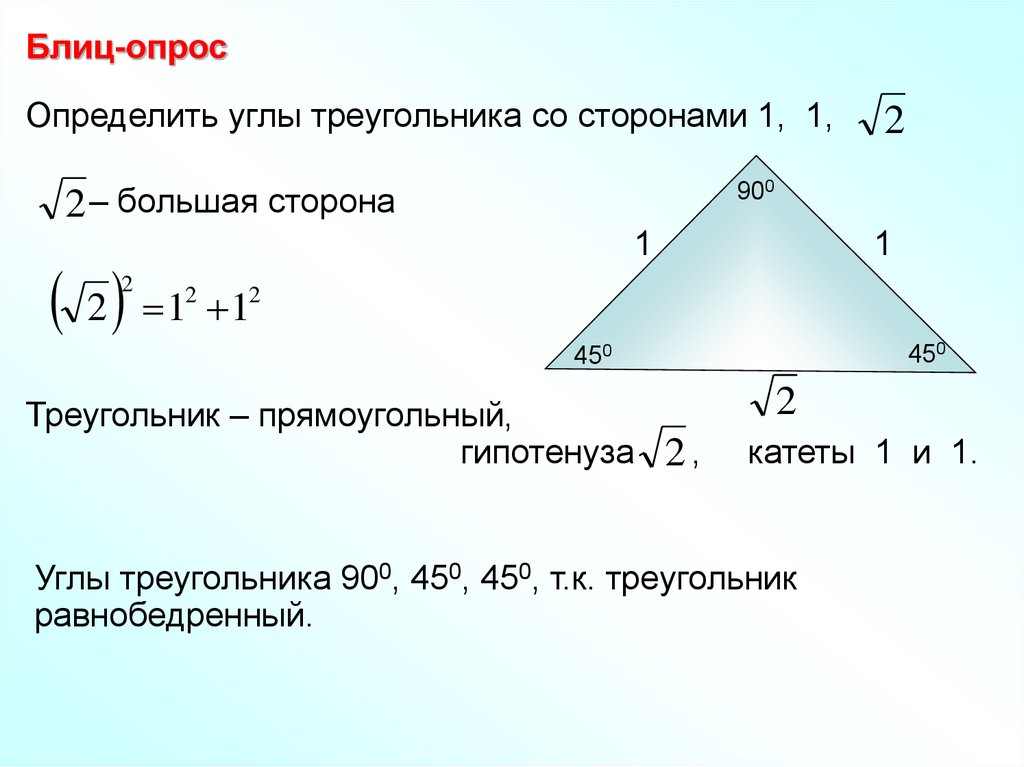
Блиц-опрос
Определить углы треугольника со сторонами 1, 1,
900
2 – большая сторона
1
2 1 1
2
2
2
1
2
450
450
Треугольник – прямоугольный,
гипотенуза 2 ,
2
катеты 1 и 1.
Углы треугольника 900, 450, 450, т.к. треугольник
равнобедренный.

14.

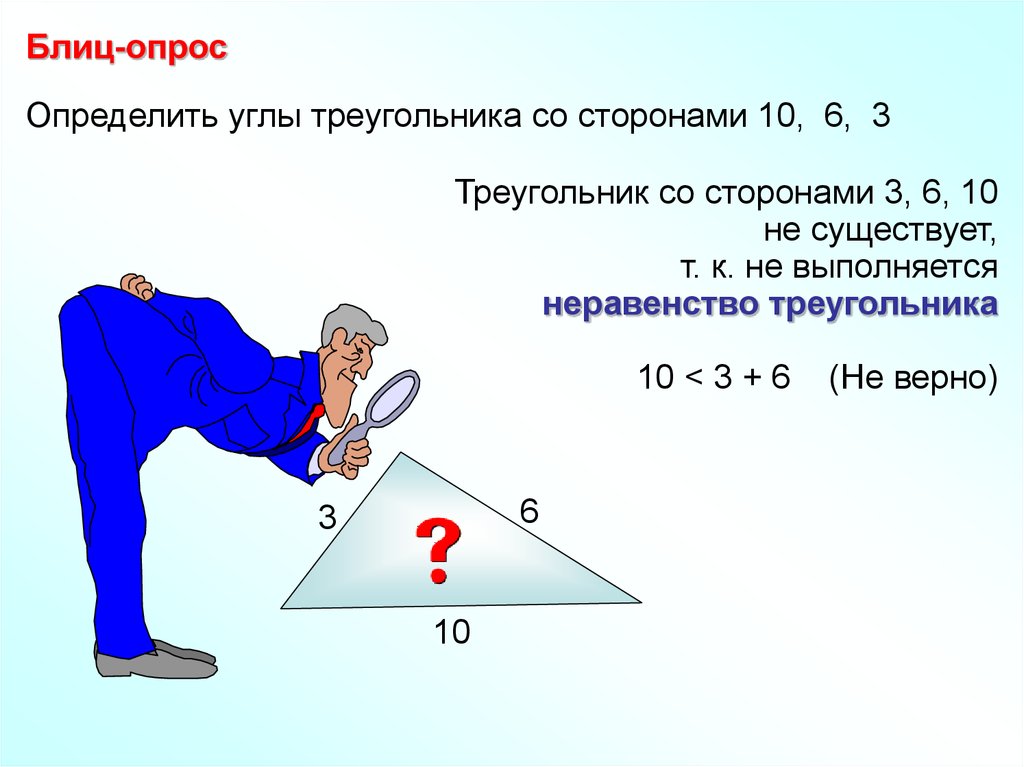
Блиц-опрос
Определить углы треугольника со сторонами 10, 6, 3
Треугольник со сторонами 3, 6, 10
не существует,
т. к. не выполняется
неравенство треугольника
10 < 3 + 6
6
3
10
(Не верно)

15.

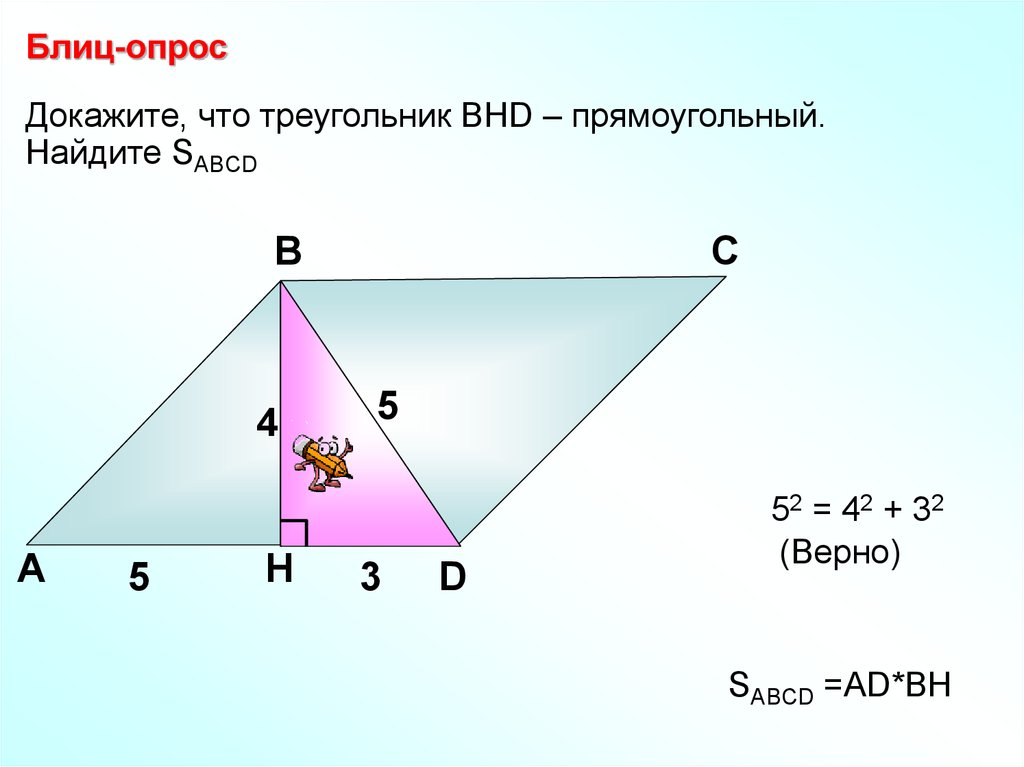
Блиц-опрос
Докажите, что треугольник ВHD – прямоугольный.
Найдите SABCD
В
4
А
5
H
С
5
3
D
52 = 42 + 32
(Верно)
SABCD =AD*BH

16.

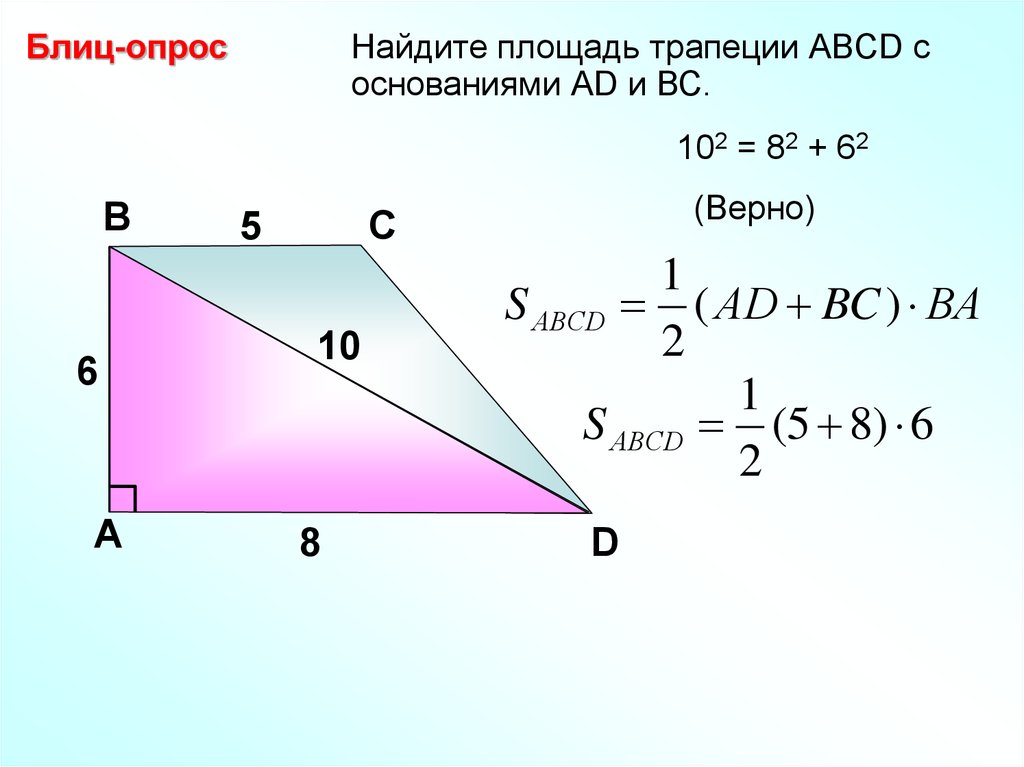
Блиц-опрос
Найдите площадь трапеции АВCD с
основаниями АD и ВС.
102 = 82 + 62
В
6
А
(Верно)
С
5
10
8
1
S АВСD ( АD BC ) ВA
2
1
S АВСD (5 8) 6
2
D

17.

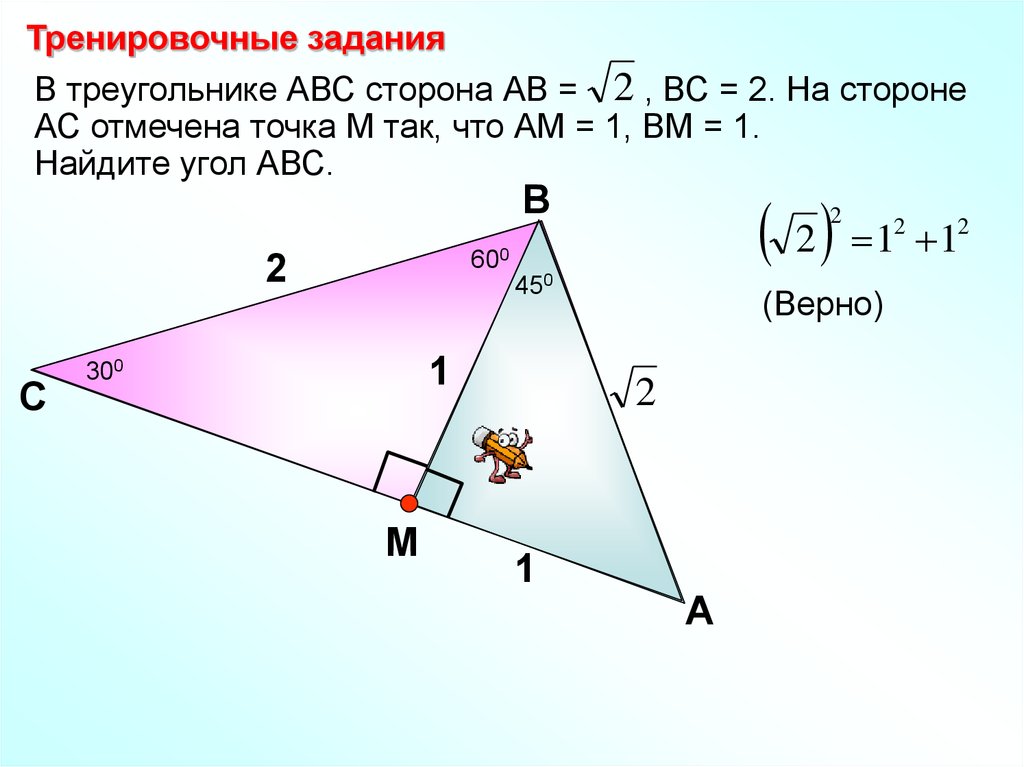
Тренировочные задания
В треугольнике АВС сторона АВ = 2 , ВС = 2. На стороне
АС отмечена точка М так, что АМ = 1, ВМ = 1.
Найдите угол АВС.
2 1 1
450
(Верно)
2
600
2
С
В
1
300
М
2
1
А
2
2

18.

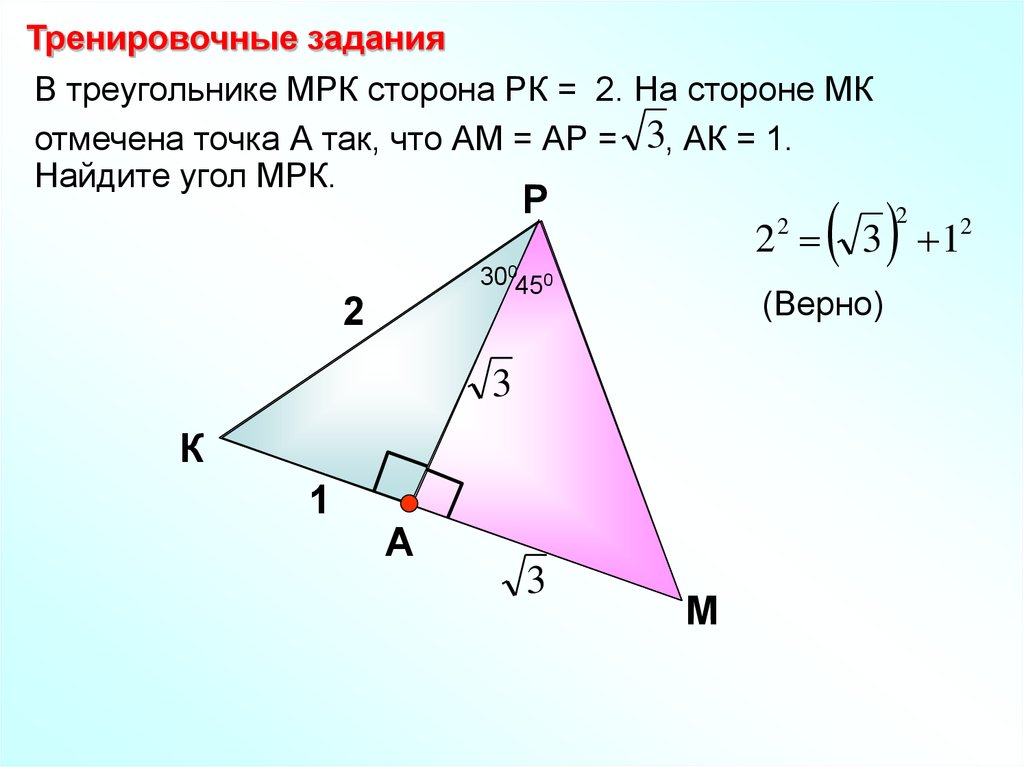
Тренировочные задания
В треугольнике МРК сторона РК = 2. На стороне МК
отмечена точка А так, что АМ = АР = 3, АК = 1.
Найдите угол МРК.
Р
2
2
300450
2
(Верно)
3
К
1
А
3
3 1
М
2
2

19.

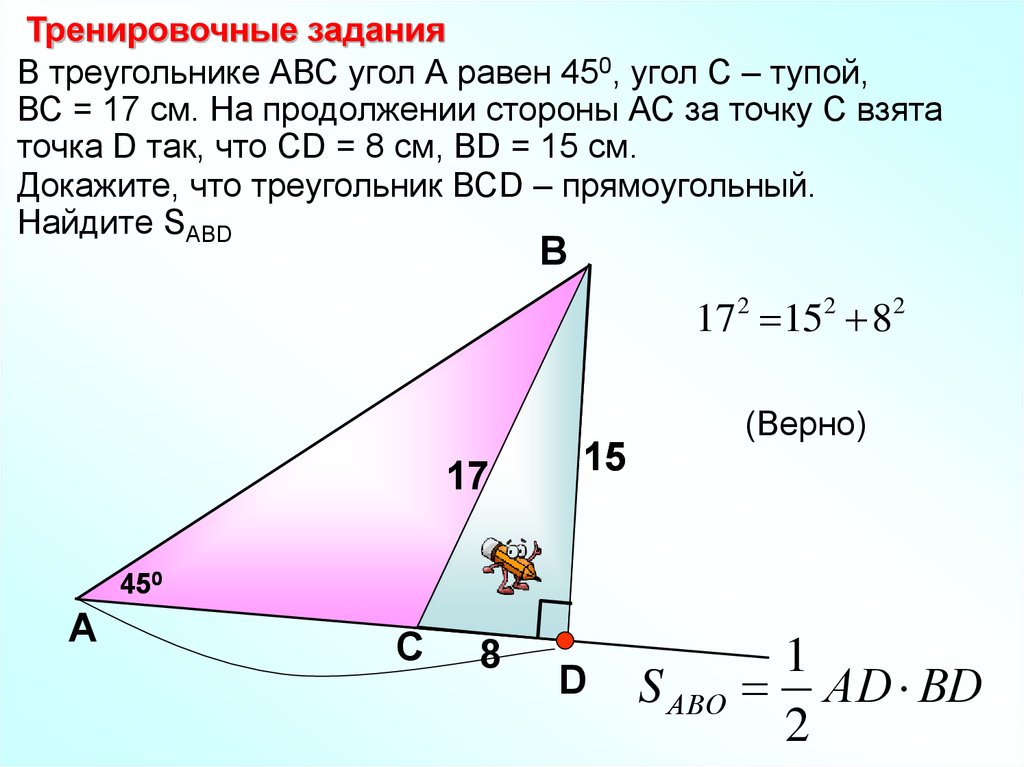
Тренировочные задания
В треугольнике АВС угол А равен 450, угол С – тупой,
ВС = 17 см. На продолжении стороны АС за точку С взята
точка D так, что CD = 8 см, BD = 15 см.
Докажите, что треугольник ВСD – прямоугольный.
Найдите SABD
В
17 2 152 82
17
(Верно)
15
450
А
С
8
D
S АВО
1
АD ВD
2

20.

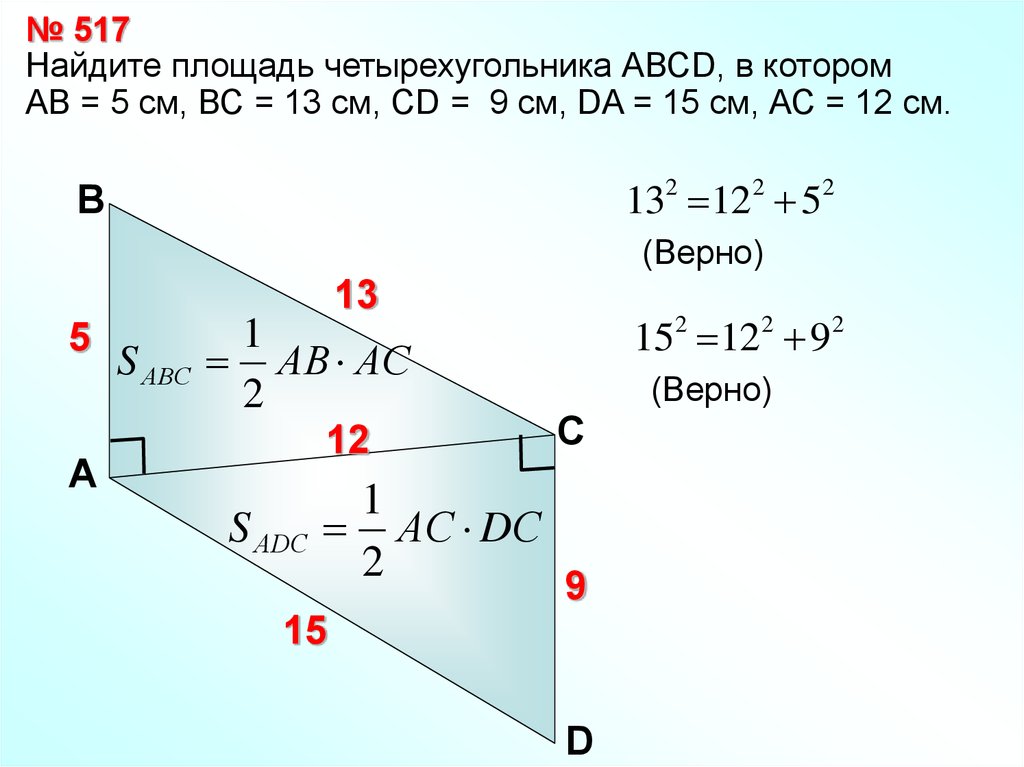
№ 517
Найдите площадь четырехугольника АВСD, в котором
АВ = 5 см, ВС = 13 см, СD = 9 см, DA = 15 см, АС = 12 см.
132 122 52
В
(Верно)
13
5
S АВС
1
АВ АС
2
12
А
S АDС
1
АС DС
2
152 122 92
(Верно)
С
9
15
D

21.

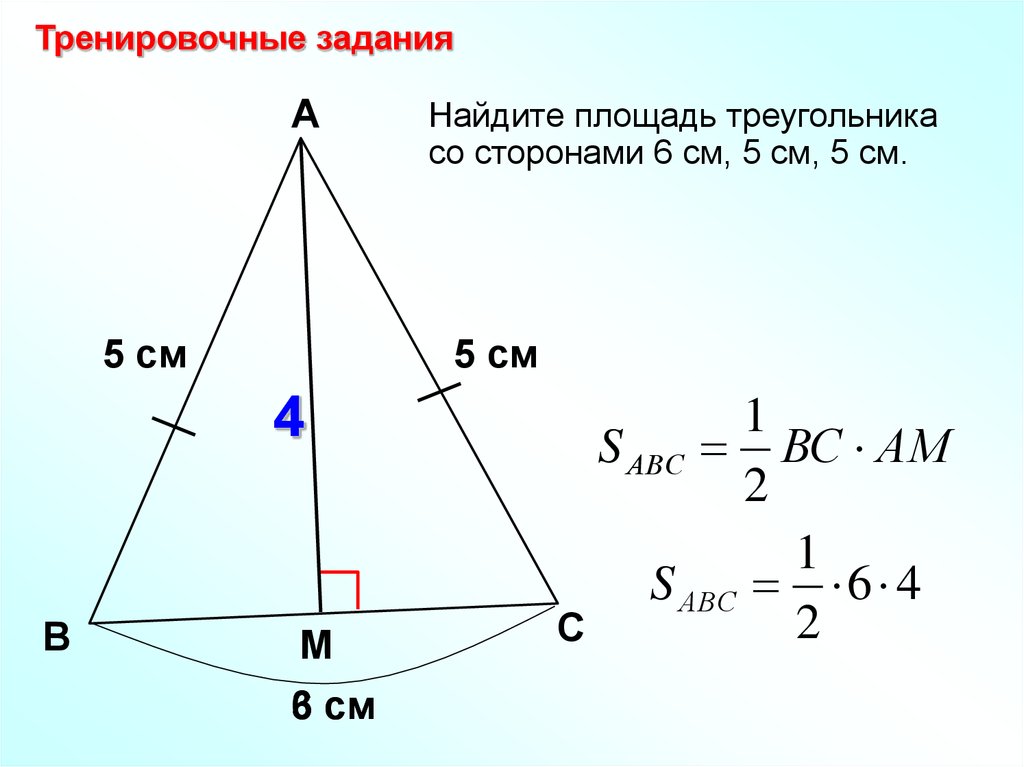
Тренировочные задания
А
5 см
5 см
4
В
Найдите площадь треугольника
со сторонами 6 см, 5 см, 5 см.
М
6 см
3
1
S АВС ВС АМ
2
1
S АВС 6 4
2
С

22.

Тренировочные задания
А
Найдите площадь треугольника
со сторонами 6 см, 8 см, 10 см.
102 82 62
(Верно)
10 см
8 см
С
6 см
1
S АВС ВС АС
2
1
S АВС 6 8
В
2

23.

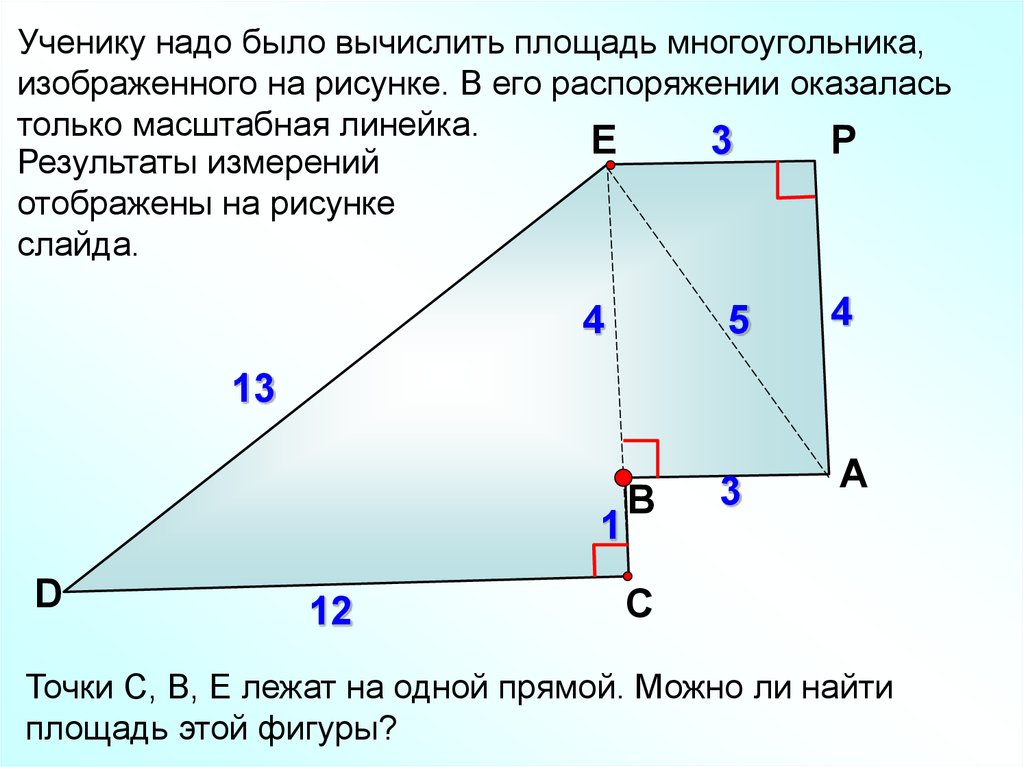
Ученику надо было вычислить площадь многоугольника,
изображенного на рисунке. В его распоряжении оказалась
только масштабная линейка.
E
3
P
Результаты измерений
отображены на рисунке
слайда.
4
5
4
3
A
13
1
D
12
В
C
Точки С, В, Е лежат на одной прямой. Можно ли найти
площадь этой фигуры?

24.

*
Диагонали некоторой трапеции равны 5 см и 12 см, а
основания 3 см и 10 см. Найдите углы между
диагоналями этой трапеции.
В
12
А
10
132 = 122 + 52
(Верно)
С
3
5
D
F

25.

*
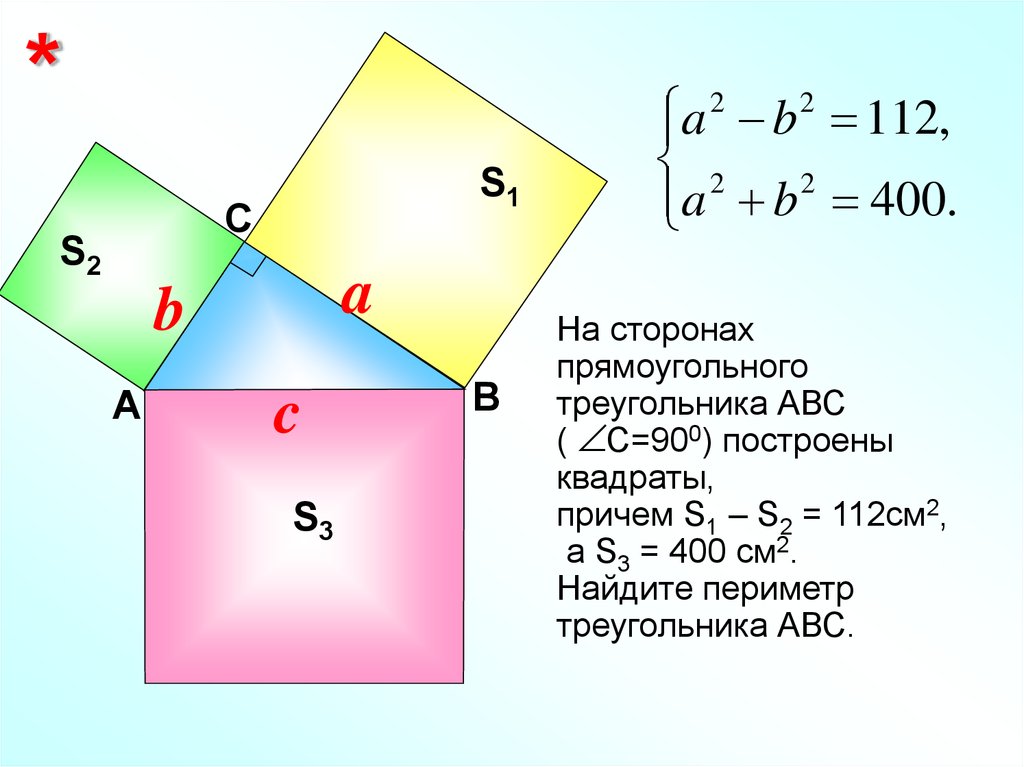
a b 112,
2
a b 2 400.
2
S1
С
S2
a
b
A
c
S3
В
2
На сторонах
прямоугольного
треугольника АВС
( С=900) построены
квадраты,
причем S1 – S2 = 112см2,
а S3 = 400 см2.
Найдите периметр
треугольника АВС.

26.

Докажите, что сумма
квадратов медиан
прямоугольного
треугольника равна 3/2
квадрата гипотенузы.
*
bM
A
С
b
2
+
Из BСM
a
2
сm
3
m21 m
2
с
2
Из АСN
F
c
N
2
a
т b
4
2
b
2
2
т2 а
4
2
c
2
т3
4
2
1
a
с
2
В
2