Похожие презентации:
Многоугольники. Выпуклые многоугольники
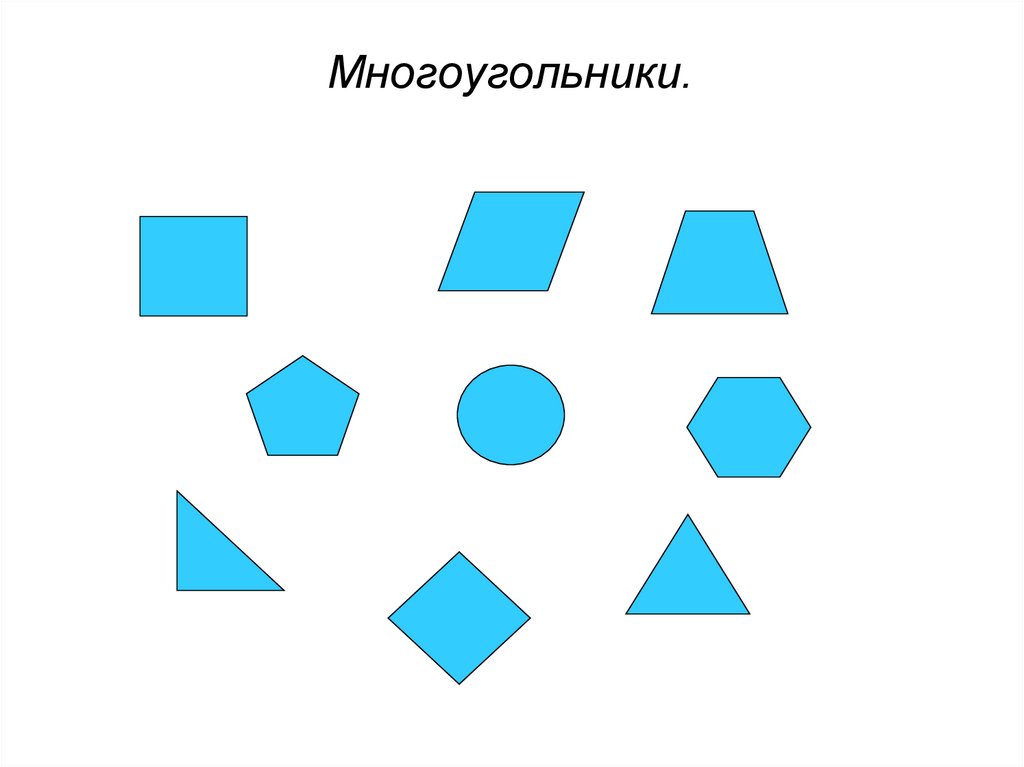
1. МНОГОУГОЛЬНИКИ
Урок геометрии в 11 классе.2. Многоугольники.
3. Ломаная.
А3А4
А6
А2
А1
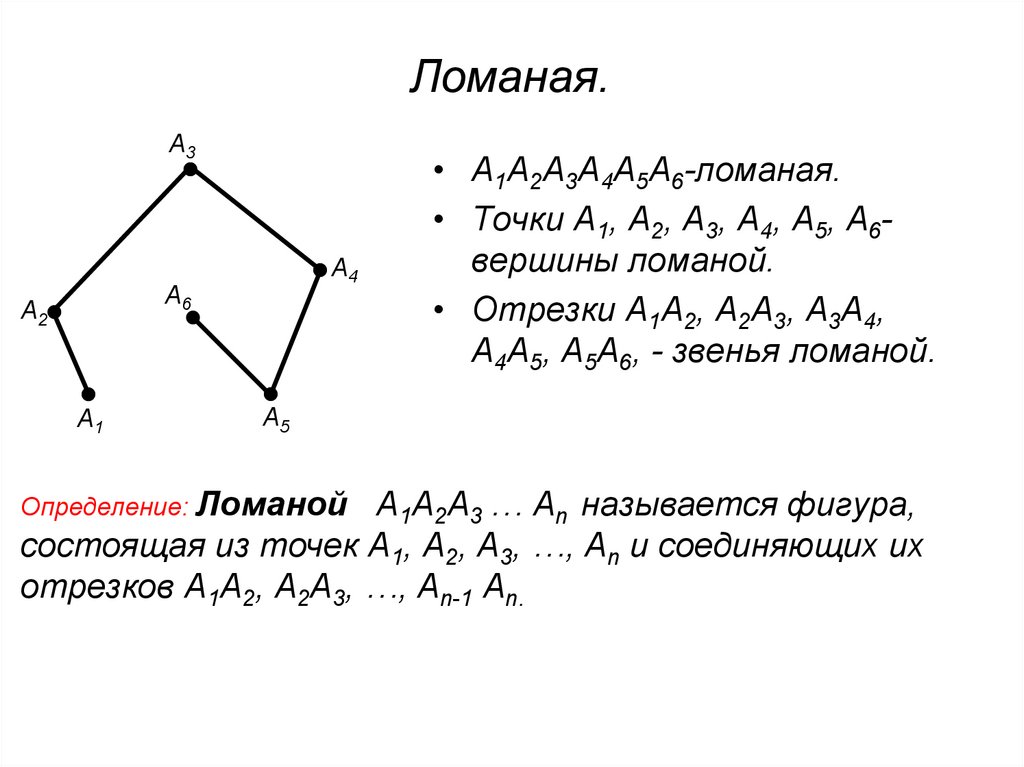
• А1А2А3А4А5А6-ломаная.
• Точки А1, А2, А3, А4, А5, А6вершины ломаной.
• Отрезки А1А2, А2А3, А3А4,
А4А5, А5А6, - звенья ломаной.
А5
Определение: Ломаной
А1А2А3 … Аn называется фигура,
состоящая из точек А1, А2, А3, …, Аn и соединяющих их
отрезков А1А2, А2А3, …, Аn-1 Аn.
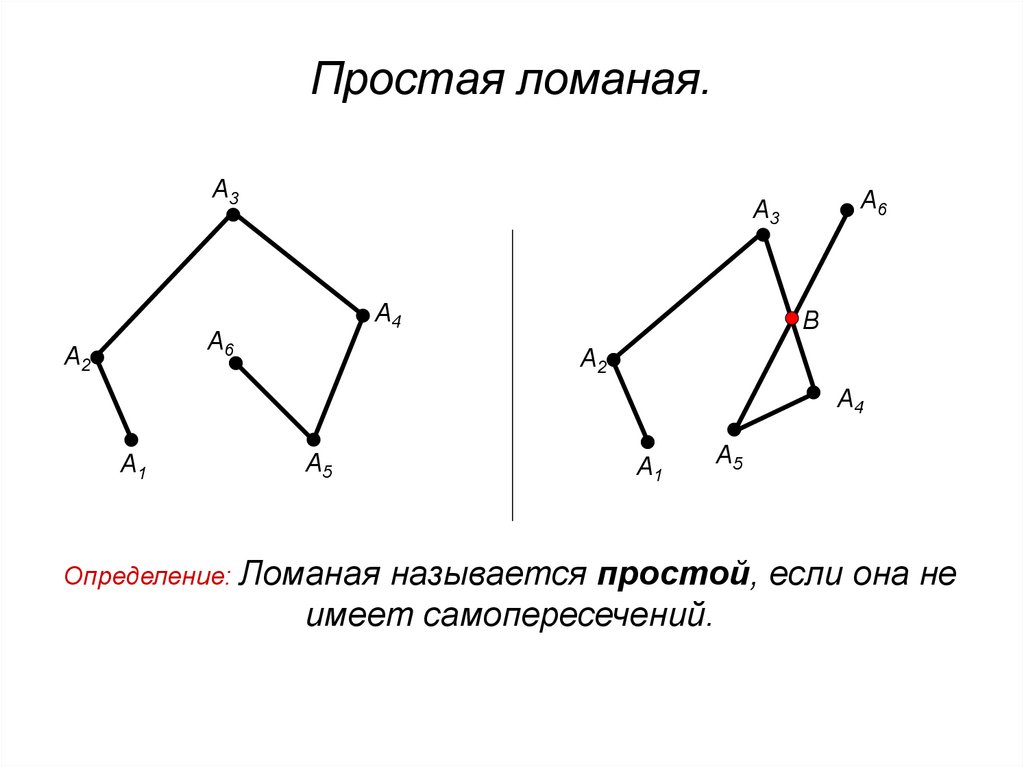
4. Простая ломаная.
А3А4
А6
А2
А6
А3
В
А2
А4
А1
А5
Определение: Ломаная
А1
А5
называется простой, если она не
имеет самопересечений.
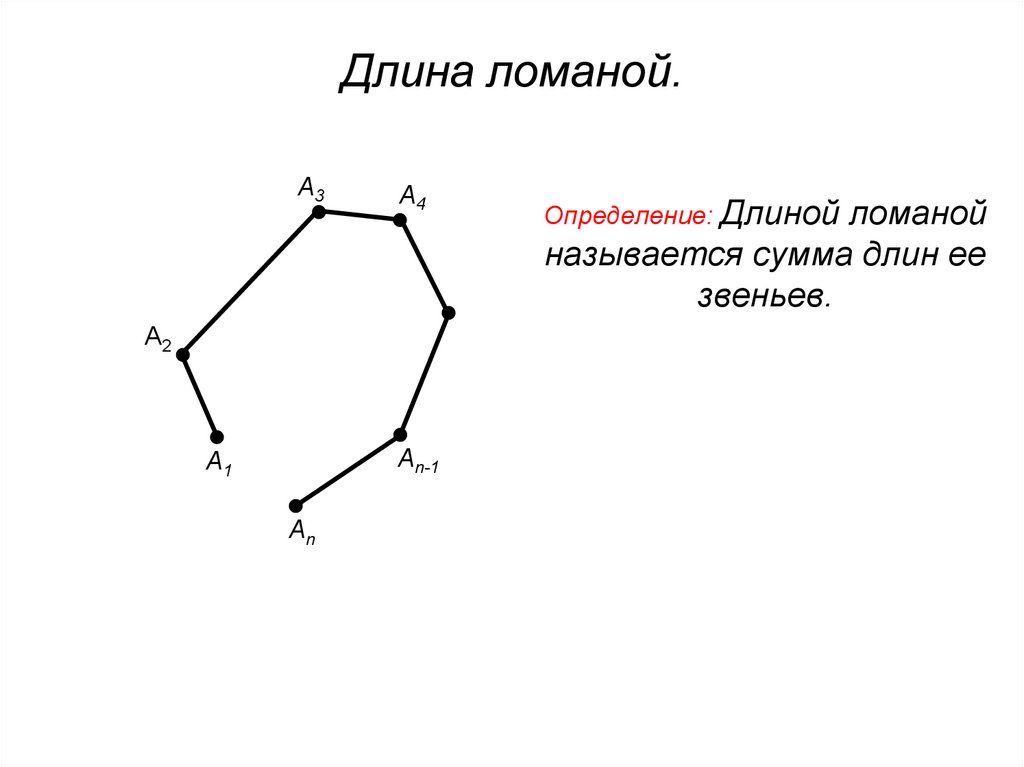
5. Длина ломаной.
А3А4
А2
Аn-1
А1
Аn
Определение: Длиной
ломаной
называется сумма длин ее
звеньев.
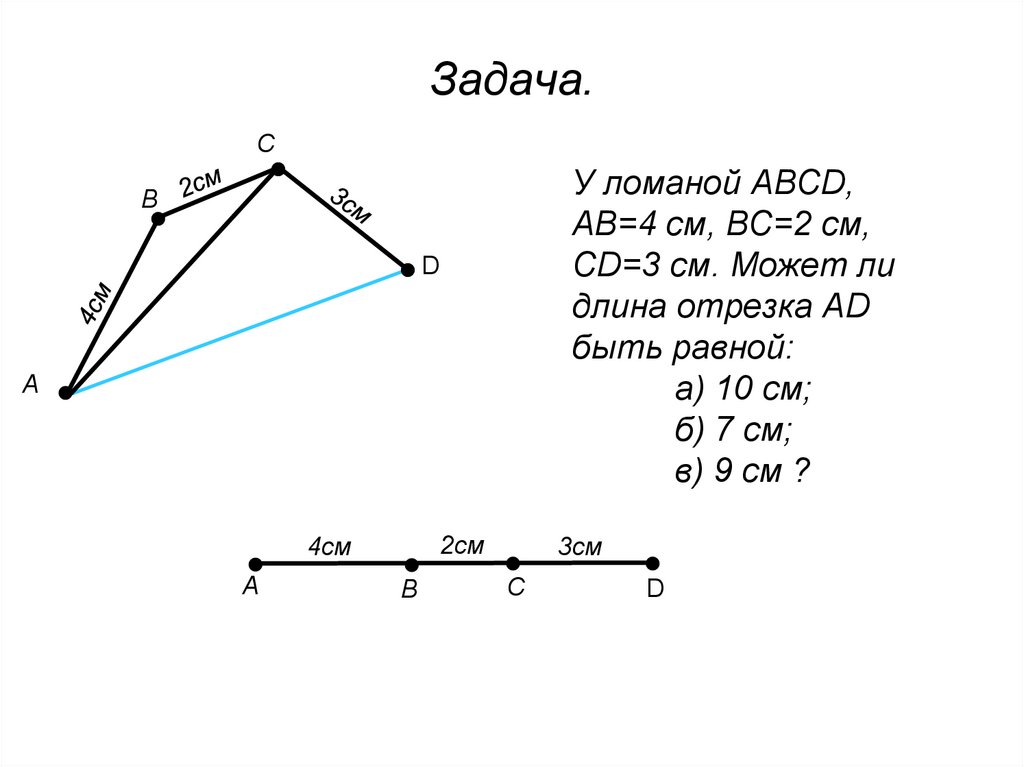
6. Задача.
СУ ломаной АВСD,
АВ=4 см, ВС=2 см,
СD=3 см. Может ли
длина отрезка АD
быть равной:
а) 10 см;
б) 7 см;
в) 9 см ?
В
D
А
2см
4см
А
В
3см
С
D
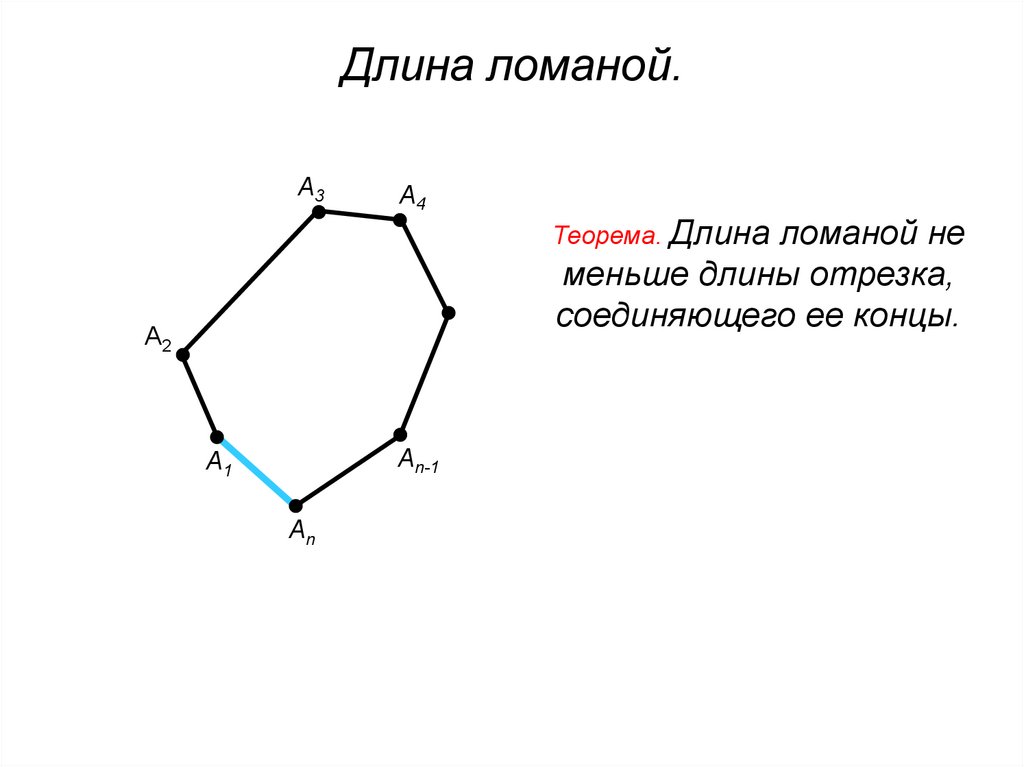
7. Длина ломаной.
А3А4
А2
Аn-1
А1
Аn
Теорема. Длина
ломаной не
меньше длины отрезка,
соединяющего ее концы.
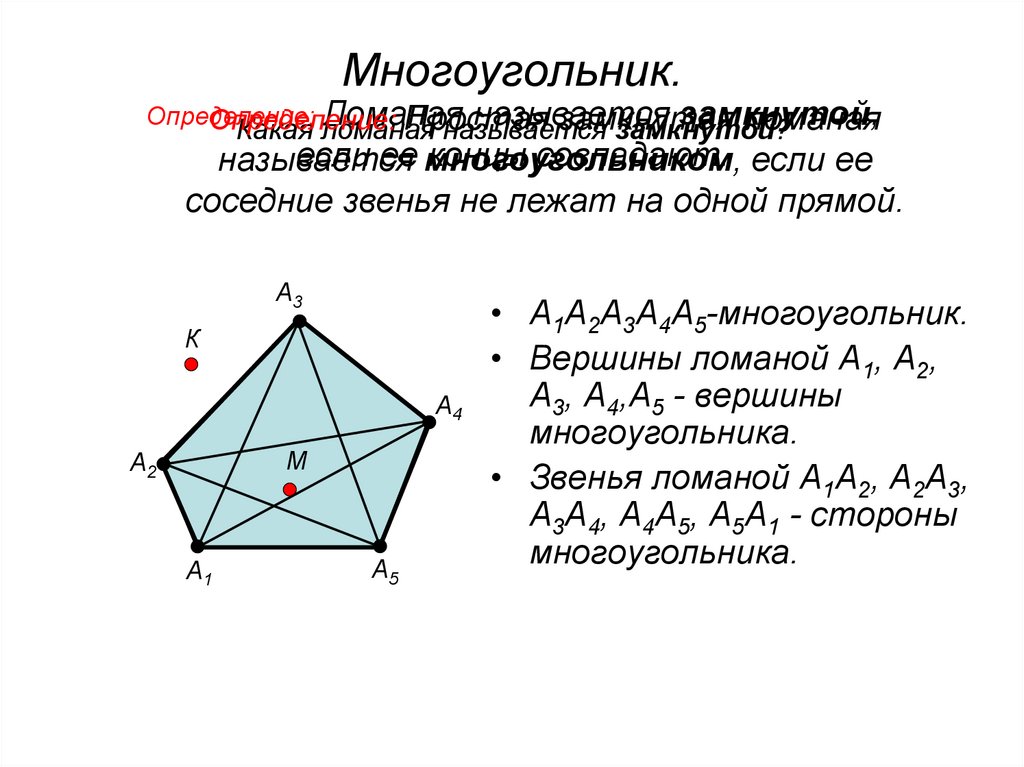
8. Многоугольник.
Определение:Ломаная
называется
замкнутой,
Определение:
Простая
замкнутая
ломаная
Какая ломаная называется замкнутой?
если ее многоугольником,
концы совпадают. если ее
называется
соседние звенья не лежат на одной прямой.
А3
К
А4
М
А2
А1
А5
• А1А2А3А4А5-многоугольник.
• Вершины ломаной А1, А2,
А3, А4,А5 - вершины
многоугольника.
• Звенья ломаной А1А2, А2А3,
А3А4, А4А5, А5А1 - стороны
многоугольника.
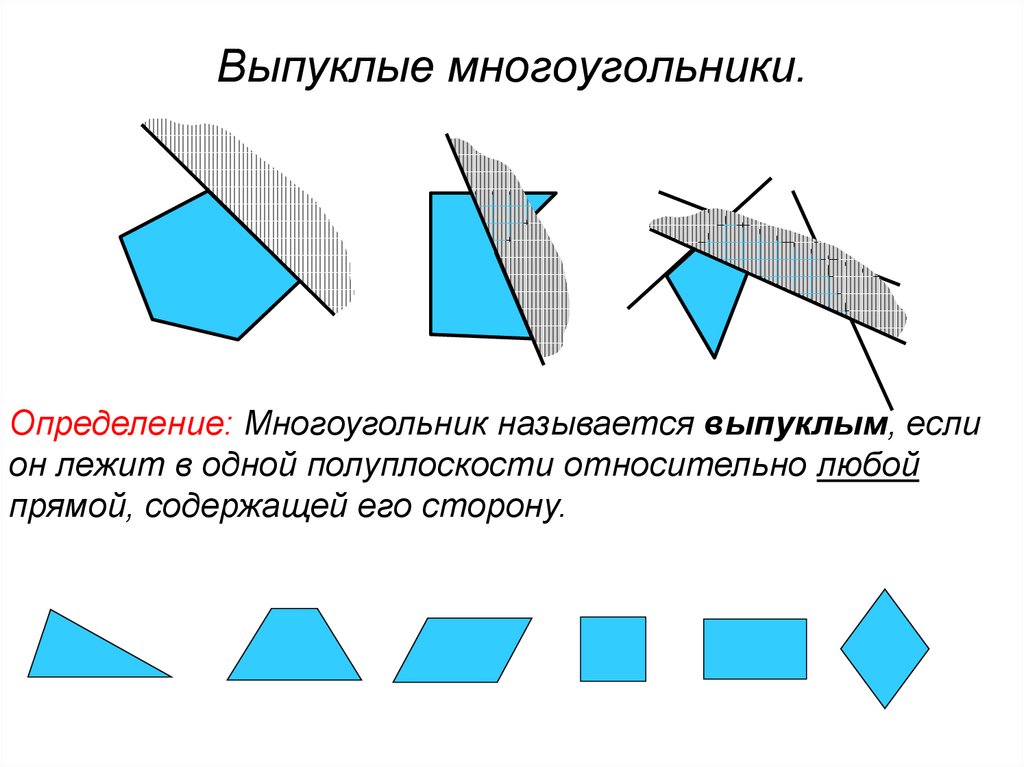
9. Выпуклые многоугольники.
Определение: Многоугольник называется выпуклым, еслион лежит в одной полуплоскости относительно любой
прямой, содержащей его сторону.
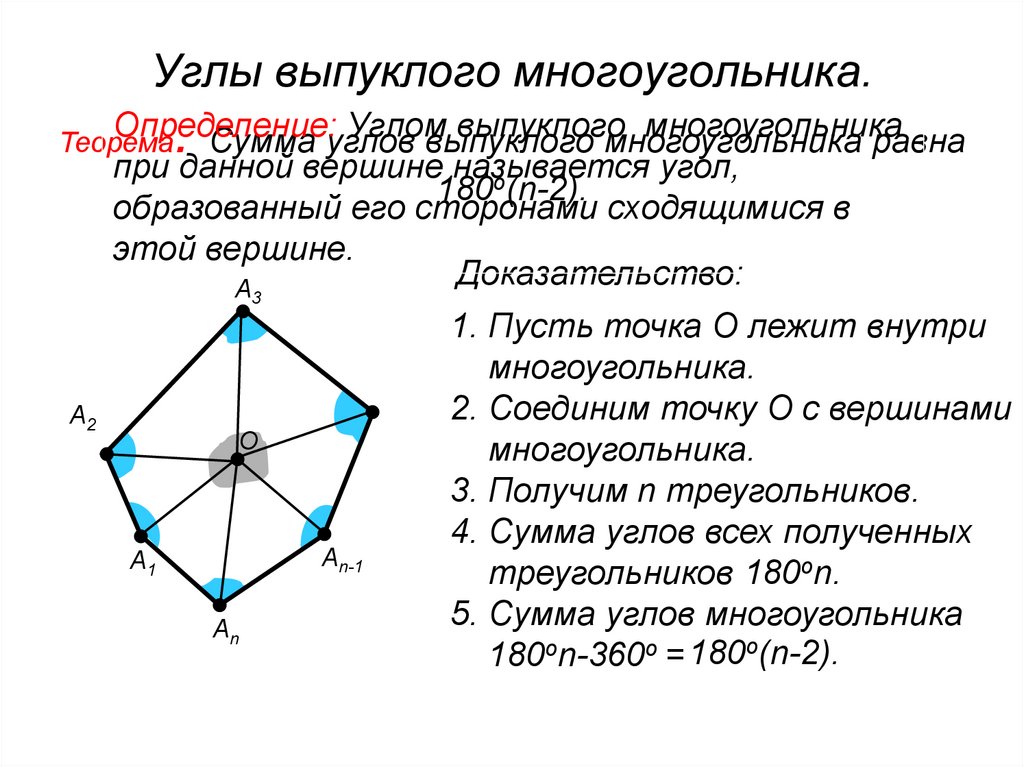
10. Углы выпуклого многоугольника.
Определение:Углом
выпуклого
многоугольника
Сумма углов
выпуклого
многоугольника
равна
при данной вершине называется
угол,
о
180 (n-2).
образованный его сторонами сходящимися в
этой вершине.
Доказательство:
А
Теорема
.
3
А2
О
Аn-1
А1
Аn
1. Пусть точка О лежит внутри
многоугольника.
2. Соединим точку О с вершинами
многоугольника.
3. Получим n треугольников.
4. Сумма углов всех полученных
треугольников 180оn.
5. Сумма углов многоугольника
180оn-360о = 180о(n-2).
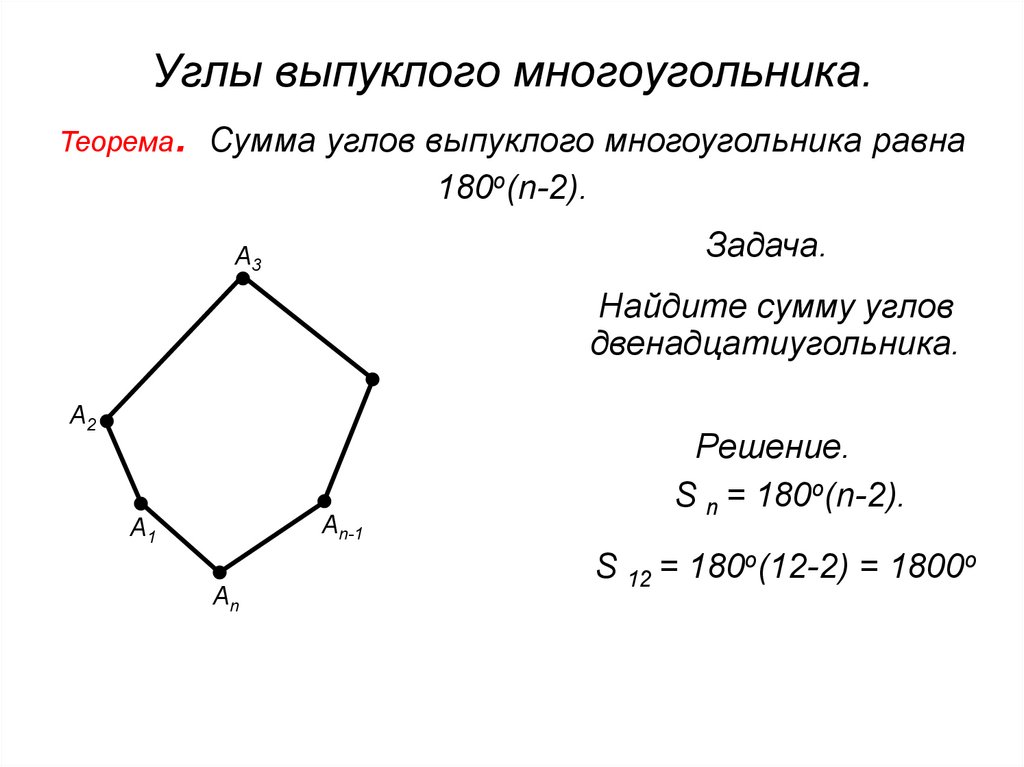
11. Углы выпуклого многоугольника.
Теорема. Сумма углов выпуклого многоугольника равна
180о(n-2).
Задача.
А3
Найдите сумму углов
двенадцатиугольника.
А2
Аn-1
А1
Аn
Решение.
S n = 180о(n-2).
S 12 = 180о(12-2) = 1800о
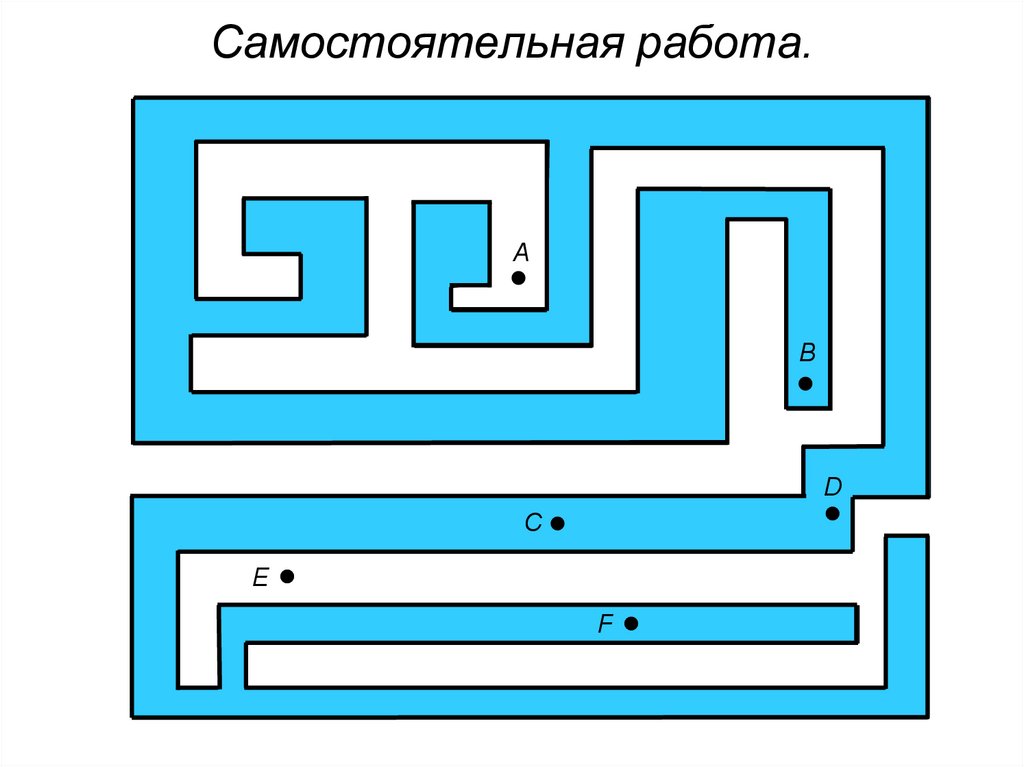
12. Самостоятельная работа.
АВ
D
С
Е
F
13. Какие фигуры на рисунке являются многоугольниками?
14.
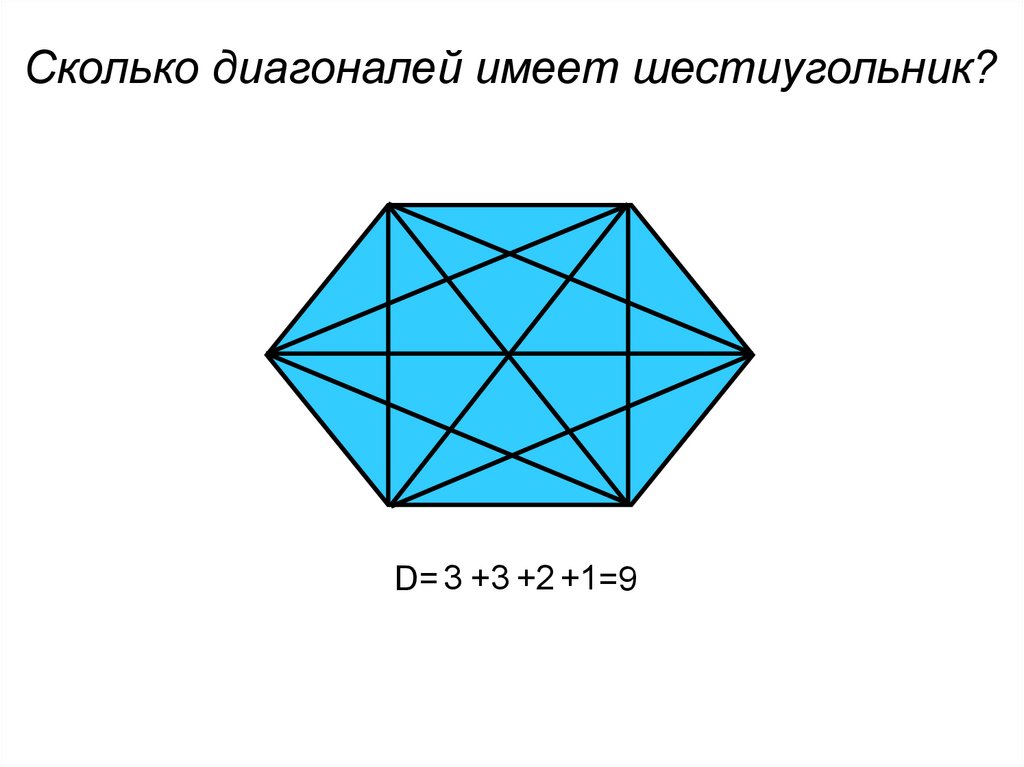
Сколько диагоналей имеет шестиугольник?D= 3 +3 +2 +1=9
15. Вычислите сумму углов выпуклого пятиугольника и десятиугольника.
Решение.S n = 180о(n-2).
S 5 = 180о(5-2) = 180о∙3 = 540о
S 10 = 180о(10-2) = 180о∙8 = 1440о
16. Домашнее задание.
§13, П.113, 114.В. 1-6 стр. 221.
№ 5, 6, 10 стр. 213.




 Математика
Математика








