Многоугольники

1.

Что общего у фигур,
изображённых на экране?

2.

2

3.

Нарисуйте в тетради фигуру,
изображённую на экране:
А1
А5
А4
Назовите отрезки, из
которых состоит
данная фигура.
А2
А3
Их можно
разделить на
смежные и
несмежные.

4.

Отрезки
смежные
А1
несмежные
А5
Смежными называются
отрезки, соединяющие
соседние вершины
фигуры.
А4
А3
А2

5.

Определение:
А
В
С
К
F
Е
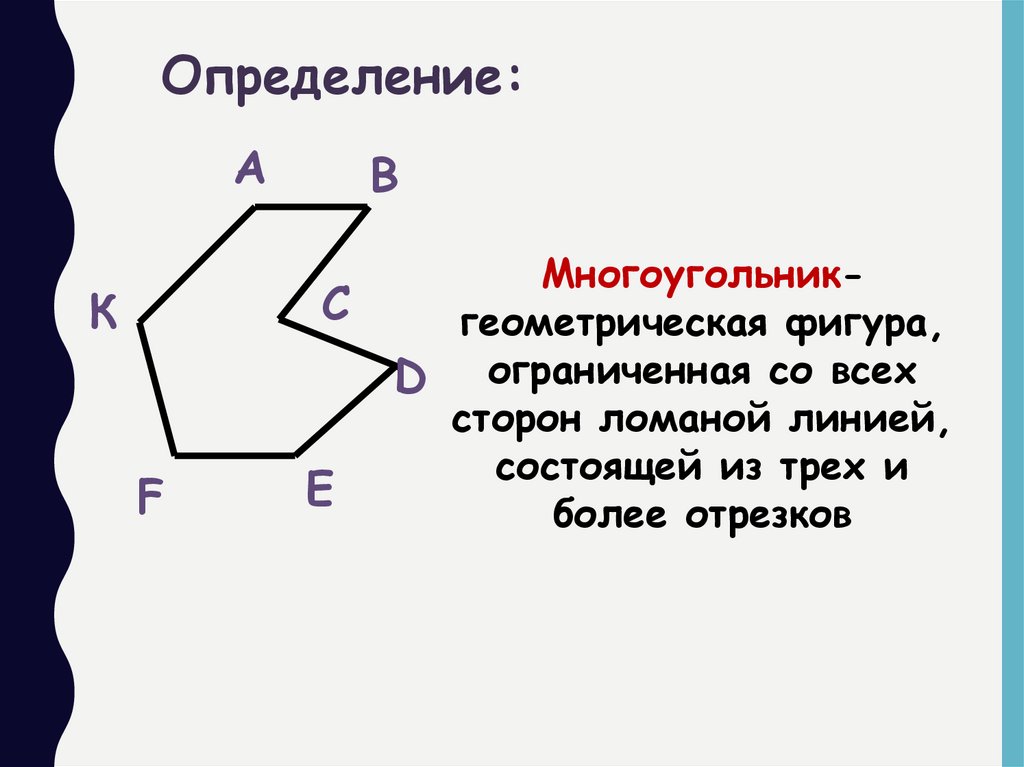
Многоугольникгеометрическая фигура,
D ограниченная со всех
сторон ломаной линией,
состоящей из трех и
более отрезков

6.

Многоугольник А1А2А3А4А5
А1
А5
А1А2, А2А3, А3А4,
А4А5, А5А1 - стороны
Р- сумма сторон
многоугольника А2 периметр
А1,А2,А3,А4,А5вершины
А4
А3
соседние
несоседние

7.

Многоугольник А1А2А3А4А5
А1
А5
А4
А2
А3
Отрезок,
соединяющий две
любые несоседние
вершины
многоугольника,
называется
диагональю.

8.

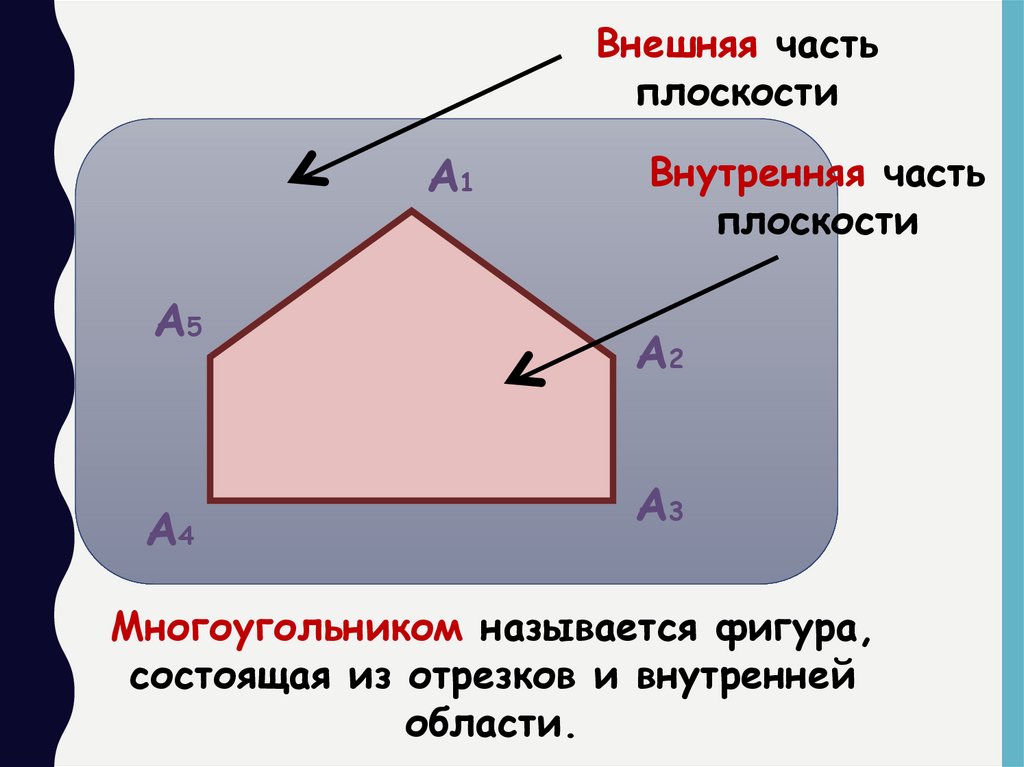
Внешняя часть
плоскости
А1
А5
А4
Внутренняя часть
плоскости
А2
А3
Многоугольником называется фигура,
состоящая из отрезков и внутренней
области.

9.

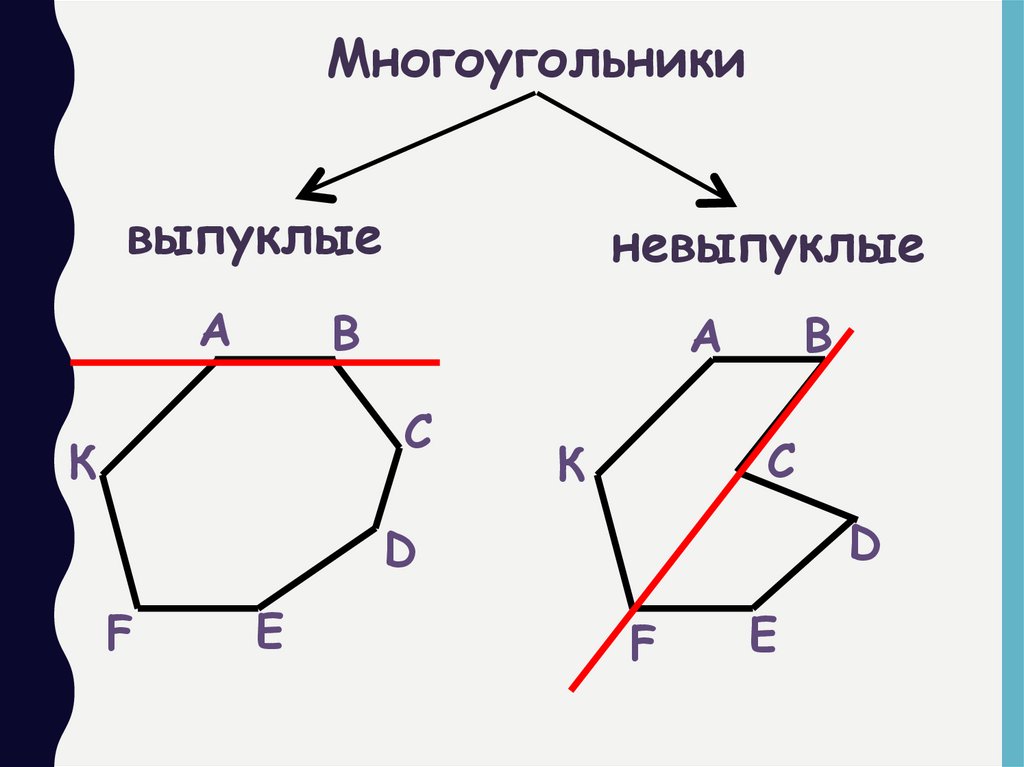
Многоугольники
выпуклые
Многоугольник
называется выпуклым,
если он лежит по
одну сторону от
прямой, проходящей
через любые две
соседние вершины.
невыпуклые
Многоугольник
называется невыпуклым,
если он лежит по разные
стороны от хотя бы
одной прямой,
проходящей через две
соседние вершины.

10.

Многоугольники
выпуклые
А
невыпуклые
В
А
С
К
В
С
К
D
D
F
Е
F
Е

11.

Нарисуйте четырёхугольник, пятиугольник и
шестиугольник.
Проведите в них диагонали, исходящие из
одной вершины.
2
3
4
Сколько треугольников образовалось в каждой
фигуре?

12.

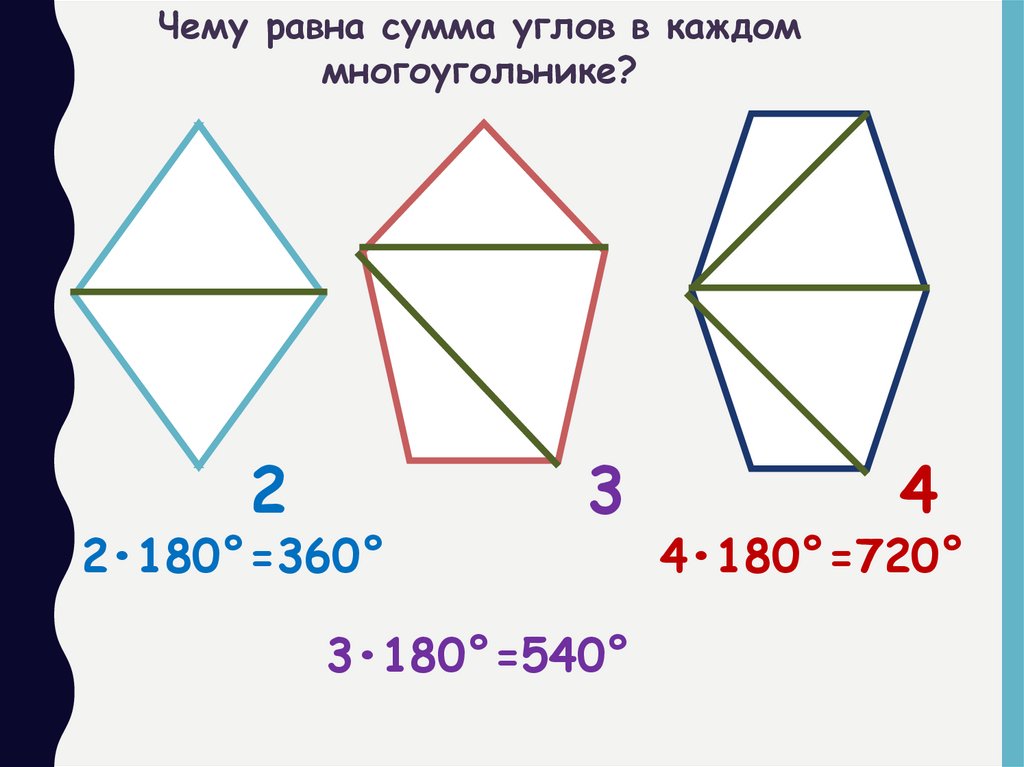
Чему равна сумма углов в каждом
многоугольнике?
2
2•180°=360°
3
3•180°=540°
4
4•180°=720°

13.

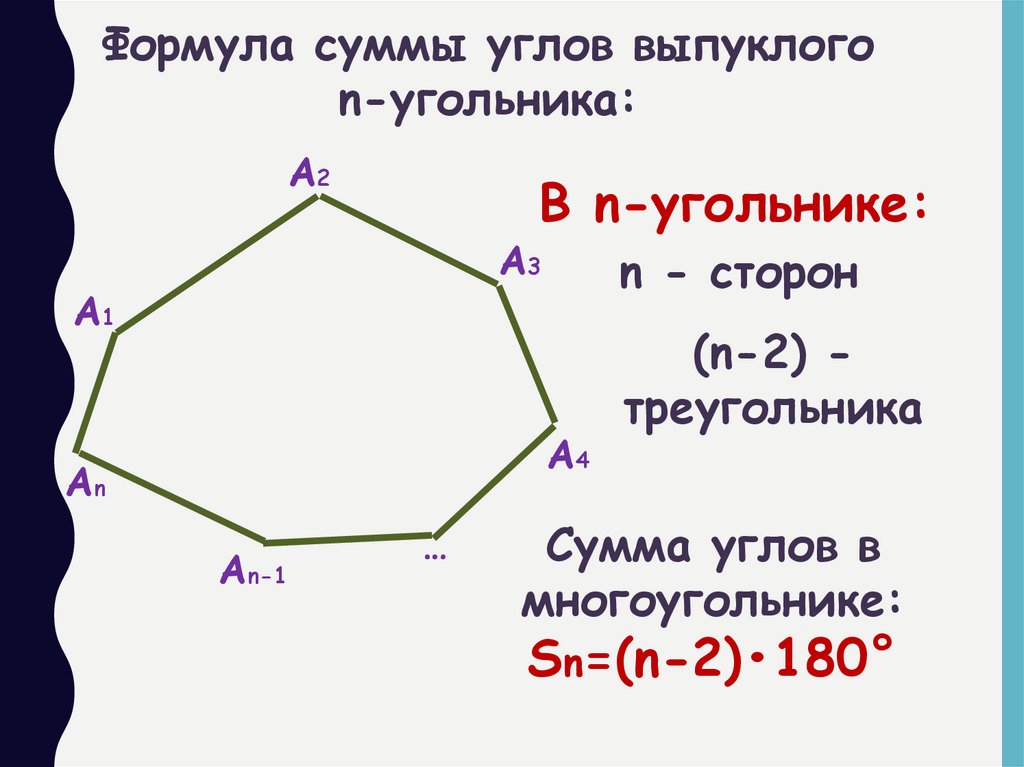
Формула суммы углов выпуклого
n-угольника:
А2
В n-угольнике:
А3
А1
n - сторон
А4
Аn
Аn-1
…
(n-2) треугольника
Сумма углов в
многоугольнике:
Sn=(n-2)•180°

14.

Четырёхугольник
В
Вершины:
А; В; С ; D
Стороны:
АВ; ВС ; СD; AD
Углы:
А; В; С; D
Определение:
А
Четырёхугольник
− геометрическая фигура, состоящая из четырёх точек и четырёх,
последовательно соединяющих их отрезков
С
D

15.

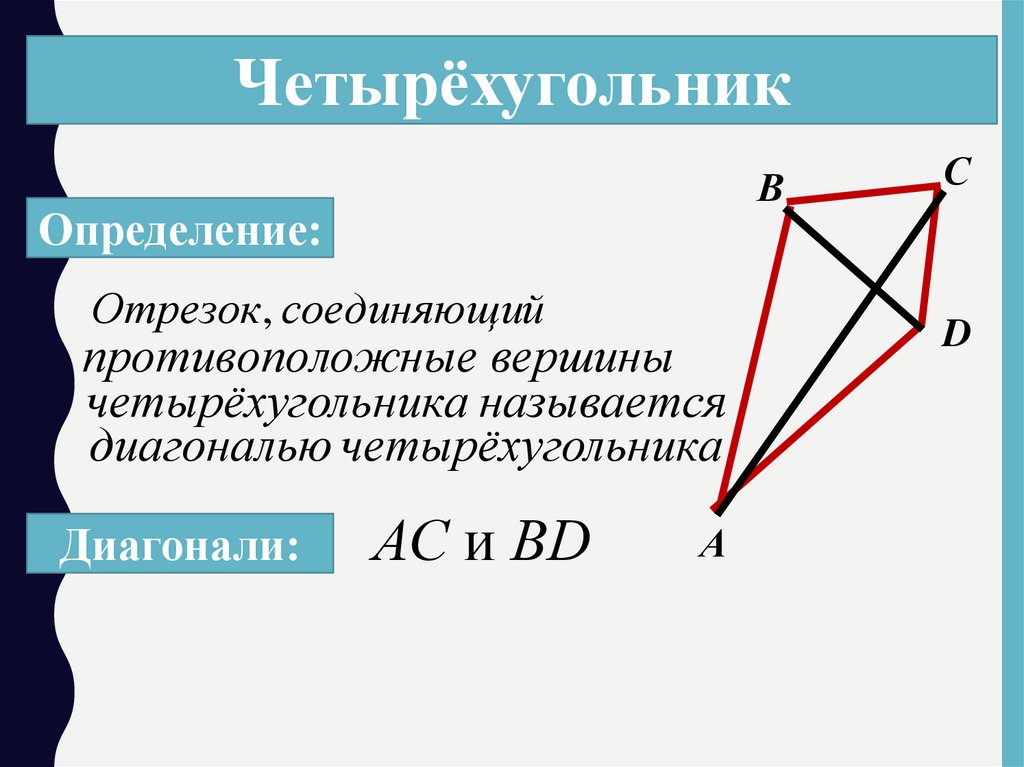
Четырёхугольник
В
Определение:
Отрезок, соединяющий
противоположные вершины
четырёхугольника называется
диагональю четырёхугольника
Диагонали:
АС и ВD
А
С
D

16.

Четырёхугольник
+
Теорема:
В
Сумма углов четырёхугольника
равна 3600
С
Проведём диагональ BD
0
ABD : A B D 180
0
CDB : C D B 180
D
A 2 B 2 D C 360 А
ч.т.д.
0
Подсказка
Док-во

17.

Задача
Один из углов четырёхугольника в 2 раза
меньше второго угла, на 20º меньше третьего и
на 40º больше четвёртого. Найдите углы
четырёхугольника.
1 х, тогда 2 2 х,
3 х 20 , а 4 х 40
3
х 2 х х 20 х 40 360
0
0
1 76 , 2 152 ,
0
0
3 96 , 4 36
4
Решение
1
2

18.

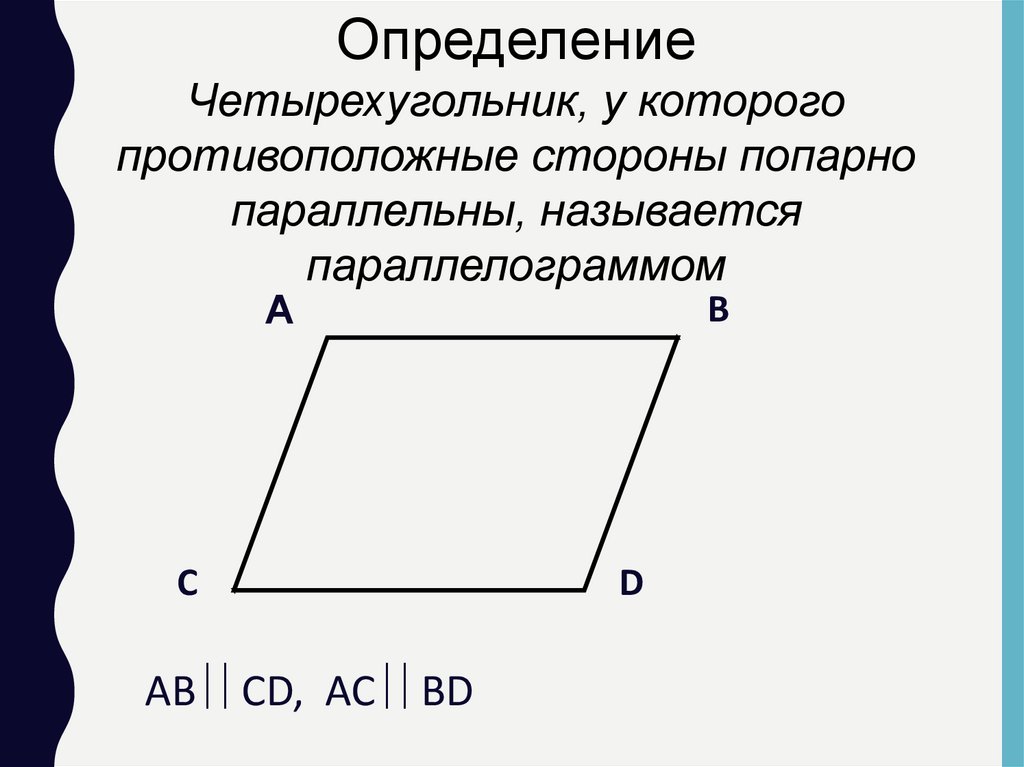
Определение
Четырехугольник, у которого
противоположные стороны попарно
параллельны, называется
параллелограммом
А
C
AB CD, AC BD
B
D

19.

КАКИМИ СВОЙСТВАМИ ОБЛАДАЕТ
ПАРАЛЛЕЛОГРАММ?
В
С
4
2
1
А
3
D

20.

СВОЙСТВО 1. В ПАРАЛЛЕЛОГРАММЕ
ПРОТИВОПОЛОЖНЫЕ СТОРОНЫ РАВНЫ
И ПРОТИВОПОЛОЖНЫЕ УГЛЫ РАВНЫ.
Дано: АВСD -
С параллелограмм
В
Доказать: 1) АВ = СD, BC = AD;
4
2
1
А
2) A = C, B = D
Доказательство:
Рассмотрим ∆ АВС и ∆ADC,
AC - общая,
1 = 2 и 3 = 4
3
D
∆ АВС = ∆ ADC (по 2-му признаку АВ = СD, BC = AD
равенства треугольников)
1 + 3 = 2 + 4 , т.е.
A = C, B = D.

21.

СВОЙСТВО 2. ДИАГОНАЛИ ПАРАЛЛЕЛОГРАММА ТОЧКОЙ
ПЕРЕСЕЧЕНИЯ ДЕЛЯТСЯ ПОПОЛАМ.
Дано: АВСD - параллелограмм
ВD AC = O
А
3
2
В
Доказать: ВО = ОD,
АО = ОС
Доказательство:
рассмотрим
∆СОD
O
∆ АОВ и
АВ = СD (противоположные
стороны параллелограмма),
1
D
4
АВ СD, ВD, AC – секущие
1= 2 и 3= 4(как накрест
лежащие углы)
С
∆ АОВ = ∆СОD (по 2-му признаку
равенства треугольников)
Следовательно: АО = ОС, ВО = ОD

22.

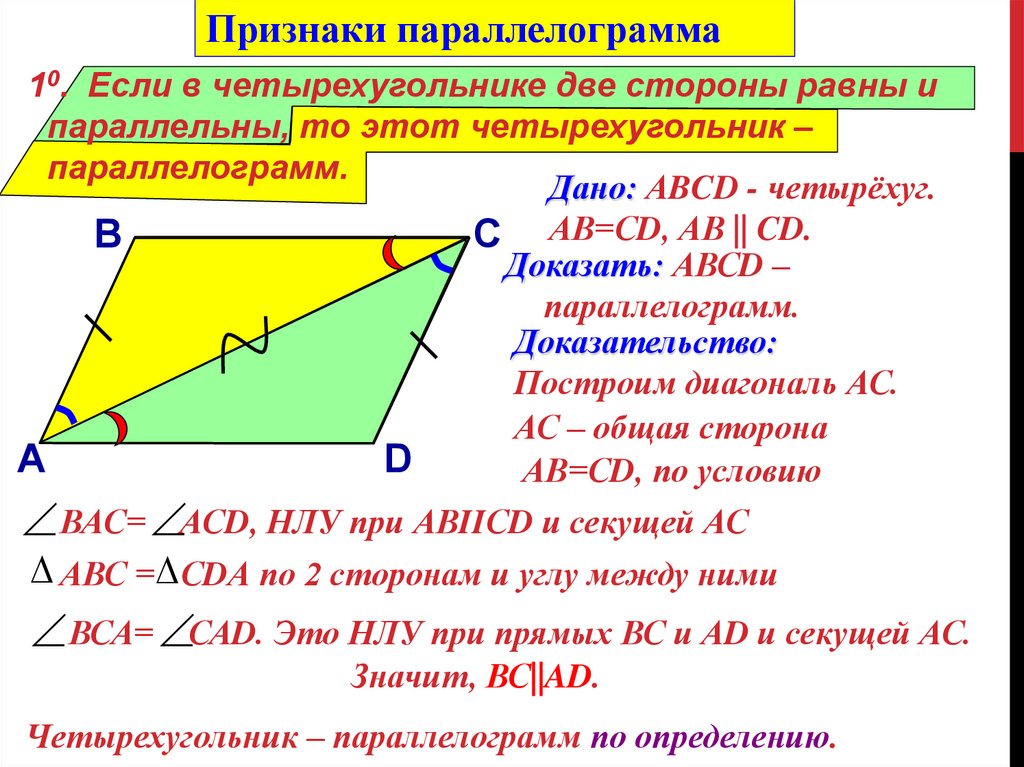
Признаки параллелограмма
10. Если в четырехугольнике две стороны равны и
параллельны, то этот четырехугольник –
параллелограмм.
Дано: АBCD - четырёхуг.
В
С АВ=СD, АВ || CD.
Доказать: АВСD –
параллелограмм.
Доказательство:
Построим диагональ АС.
АС – общая сторона
А
D
АВ=СD, по условию
ВАС= АСD, НЛУ при АВIIСD и секущей АС
АВС = СDА по 2 сторонам и углу между ними
ВСА= САD. Это НЛУ при прямых ВС и АD и секущей АС.
Значит, ВС||AD.
Четырехугольник – параллелограмм по определению.

23.

Признаки параллелограмма
20. Если в четырехугольнике противоположные
стороны попарно равны, то этот четырехугольник –
параллелограмм.
Дано: АВ=СD, ВС=АD.
В
А
С Доказать: АВСD –
параллелограмм.
Доказательство:
Построим диагональ АС.
АС – общая сторона
АВ=СD, по условию
D
ВС=АD, по условию
АВС = СDА по трем сторонам
ВАС= АСD. Это НЛУ при прямых АВ и СD и секущей АС.
Значит, АВ||СD.
АВ=СD, по условию.
Четырехугольник – параллелограмм по признаку 10.

24.

30. Если в четырехугольнике диагонали пересекаются
и точкой пересечения делятся пополам, то этот
четырехугольник – параллелограмм.
Дано: АС ВD О, О середина АС и ВD.
В
А
С Доказать: АВСD –
параллелограмм.
О
Доказательство:
АО=ОС, по условию
ВО=ОD, по условию
АОВ= СОD, как
D
вертикальные
АОВ = СОD по первому признаку
Отсюда, АВ=СD
ВАО= ОСD. Это НЛУ при прямых АВ и СD и секущей АС.
Значит, АВ||СD.
Четырехугольник – параллелограмм по признаку 10.

25.

1.
Zb
2.
Ам
3.
Ывс
4.
ымв