Параллельные прямые

1.

Смирнова Елена Евгеньевна
ГБОУ СОШ № 277

2.

b
а
М
а
b
а∩b=М
а║b

3.

4.

1.Определение параллельных прямых - Евклид (III век до
н.э.), в трудах «Начала»
«Параллельные суть прямые, которые находясь в одной
плоскости и будучи продолжены в обе стороны неограниченно
ни с той, ни с другой стороны между собой не встречаются».
2.Посидоний (I век до н.э.)
«Две прямые, лежащие в одной плоскости,
равноотстоящие друг от друга»
3.Древнегреческий учёный Папп (вторая половина III века до
н.э.) ввёл символ параллельности прямых =. Впоследствии
английский экономист Рикардо (1772- 1823) этот символ
использовал как знак равенства. Только в 18 веке стали
использовать символ ||.

5.

При пересечении прямых a и b cекущей c образуются
восемь углов. Некоторые пары этих углов имеют
специальные названия:
с
1
а
4
5
b
8
3
6
7
2

6.

Если при пересечении двух прямых секущeй накрест лежащие
углы равны,то прямые параллельны.
с
2
3
а
6
b
7
5
8
1
4
<1=<7
<2=<8
<3=<5
<4=<6
а║b

7.

Если при пересечении двух прямых секущей соответственные
углы равны,то прямые параллельны.
с
2
3
а
6
b
7
5
8
1
4
<1=<5
<2=<6
<4=<8
<3=<7
а║b

8.

Если при пересечении двух прямых секущей сумма
односторонних углов равна 180°, то прямые параллельны.
с
2
3
а
6
b
7
4
5
8
1
<1+<8=180°
<2+<7=180°
<3+<6=180°
<4+<5=180°
а║b

9.

№186
с
1
4
2
а
3
8
7
5
6
Дано: а и b – прямые, с –
секущая.
b а) <1=37°, <7=143°
б) <1=<6
в) <1=45°, <7=3•<3
Доказать: а║b

10.

а) Доказательство:
1) <1=<3=37°( вертикальные)
2) <7=<5=143°( вертикальные)
3) <3,<5 – односторонние углы при прямых а, b и секущей с.
<3+<5=37°+ 143°=180°;
аΙ Ι b по признаку параллельности прямых.
б) Доказательство:
1) <1=<3( вертикальные), <6=<8( вертикальные), <1=<6( по условию),значит
<3=<8, а так как <3 и <8 накрест лежащие при прямых а и b и секущей с ,
то аΙ Ι b по признаку параллельности прямых.
в) Доказательство:
1) <1=<3=45°( вертикальные)
Так как <7=3•<3, то <7=135°; <5=<7=135°( вертикальные).
2) <3, <5 – односторонние углы при прямых а и b и секущей с
<3+<5=45°+ 135°=180°, значит а Ι Ι b по признаку параллельности
прямых.

11.

№190
В
D
35°
А
Дано:ΔАВС
АВ=ВС, АD=DЕ,<С=70°,
<ЕАС=35°
Е
Доказать: DЕ║АС.
70°
С

12.

Доказательство
1) Так как АВ=ВС, то <А=<С=70°( свойство равнобедренного
треугольника)
2) Так как <ЕАС=35°, <А=70°, <DАЕ=35°
3) Так как ▲АDЕ- равнобедренный, то <DАЕ=<DЕА=35°(
свойство )
4) <DЕА=<ЕАС=35°, <DЕА и <ЕАС- накрест лежащие при
прямых DЕ и АС и секущей АЕ, значит DЕ║АС ( по признаку
параллельных прямых) , что и требовалось доказать.

13.

Практические способы построения параллельных прямых
b
c
bIIc
А

14.

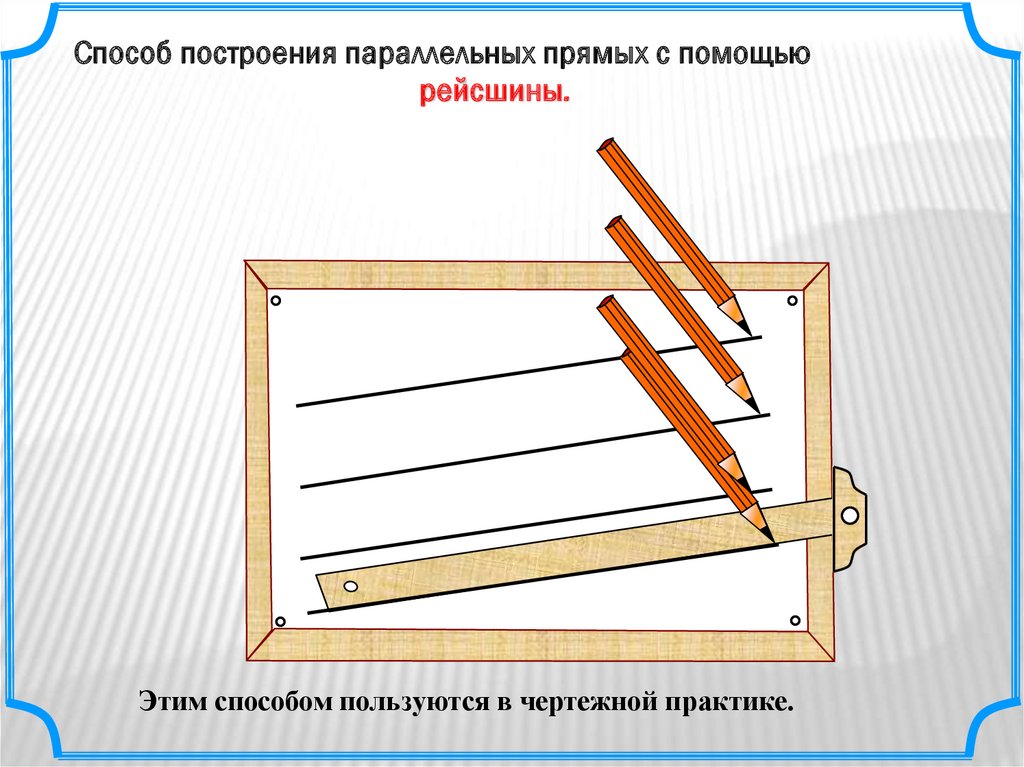
Способ построения параллельных прямых с помощью
рейсшины.
Этим способом пользуются в чертежной практике.

15.

Задача № 193
C
Дано:
D
▲ АВС
˂А=40°; B=70°;
ВС- биссектриса ˂ABD.
Доказать:
ACII ВD
70°
B
40°
A

16.

Доказательство:
1) Так как BC- биссектриса ˂DBA и ˂ABC=70°, то ˂DBA=140°
2) ˂DBA и ˂A- односторонние при прямых ВD , АС и секущей АВ;
˂DBA+˂A=140°+40°=180°; то BDIIAC( по признаку параллельных прямых) ч. Т. Д.

17.

18.

19.

20.

21.

№ 187
№ 188
№ 189