Похожие презентации:
Значение выражения. Подготовка к ОГЭ. Вариант № 1 (май)
1.
Подготовка к ОГЭВариант № 1 (май)
8.05
2.
№6• Найдите значение выражения
3.
Ответ: −2.4.
7. Какое из следующих неравенств не следует из неравенстваВ ответе укажите номер правильного варианта.
1)
2)
3)
4)
?
5.
Решение.Приведем исходное неравенство соотвествующему виду:
1)
2)
3)
4)
Неравенство
не следует из исходного неравенства.
Правильный ответ указан под номером 2.
6.
8. Какое из следующих чисел является наименьшим?В ответе укажите номер правильного варианта.
1) 1,7·10−3
2) 2,3·10−4
3) 4,5·10−3
4) 8,9·10−4
7.
Числа здесь представлены в стандартном виде. Поэтому из них наименьшим будет то, котороеимеет наименьший показатель степени десяти. Если показатели равны, то наименьшим будет
число, имеющее наименьшую мантиссу. Таким образом, среди представленных чисел наименьшее
—
Правильный ответ указан под номером: 2.
8.
9. Решите систему уравненийВ ответе запишите сумму решений системы.
О т в е т : −1.
9.
10. Какова вероятность того, что случайно выбранное натуральное число от 15 до 29 делитсяна 5?
Решение.
Чисел от 15 до 29 — 15 штук. Среди них на 5 делится только 3 числа. Таким образом,
вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5
равна
10.
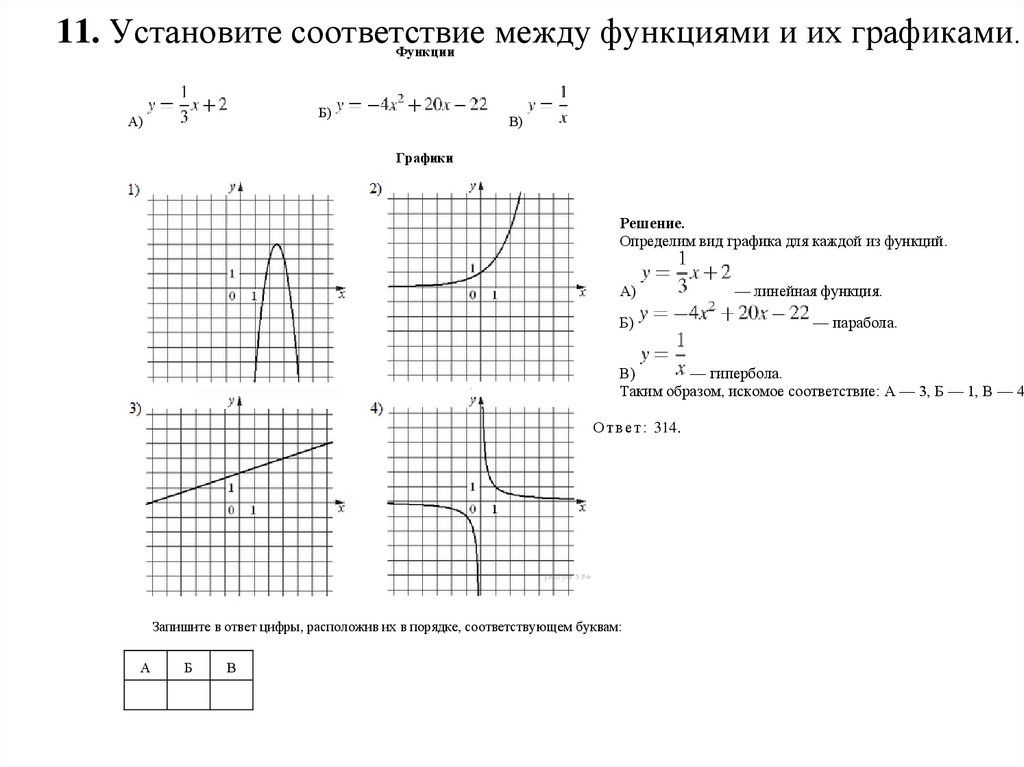
11. Установите соответствиемежду функциями и их графиками.
Функции
Б)
А)
В)
Графики
Решение.
Определим вид графика для каждой из функций.
А)
Б)
— линейная функция.
— парабола.
В)
— гипербола.
Таким образом, искомое соответствие: A — 3, Б — 1, В — 4.
О т в е т : 314.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
А
Б
В
11.
12. В арифметической прогрессиичетвёртый член этой прогрессии.
Решение.
Имеем:
О т в е т : 7.
известно, что
. Найдите
12.
13. Найдите значение выраженияРешение.
Упростим выражение:
Подставим в полученное выражение значение
Ответ: 1.
при
13.
14. Длину биссектрисы треугольника, проведённой к сторонеформуле
Решение.
. Вычислите
Выразим из данной формулы
Подставляя, получаем:
О т в е т : 0,8.
:
, если
, можно вычи
.
14.
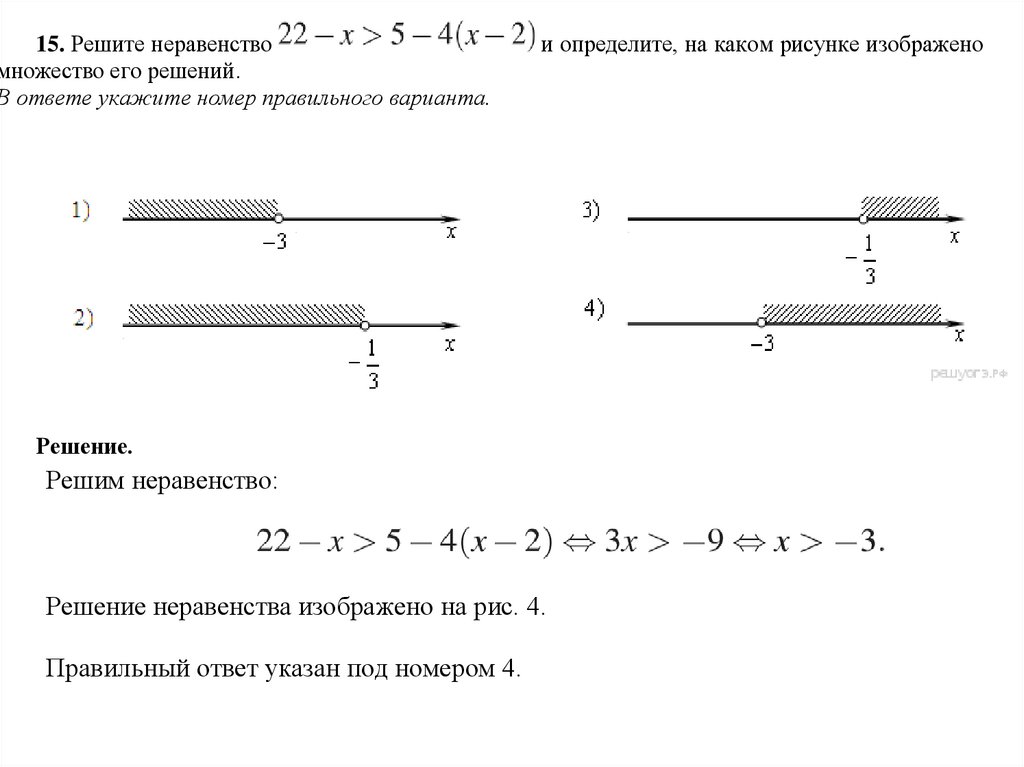
15. Решите неравенствомножество его решений.
В ответе укажите номер правильного варианта.
и определите, на каком рисунке изображено
Решение.
Решим неравенство:
Решение неравенства изображено на рис. 4.
Правильный ответ указан под номером 4.
15.
16.Прямые m и n параллельны. Найдите ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в градусах.
Решение.
Введём обозначение, как показано на рисунке. Углы 1 и 4 соответственные, поэтому
∠4 = ∠1 = 22°. Углы 2, 3 и 4 — это углы одного треугольника, сумма углов треугольника равна
180°, откуда ∠3 = 180° − 22° − 72° = 86°.
О т в е т : 86.
16.
17. На окружности с центром в точке отмечены точки именьшей дуги
равна 50. Найдите длину большей дуги
.
Решение.
Пусть длина большей дуги
равна
мере, поэтому имеет место отношение:
О т в е т : 400
так, что
. Длина
Длина дуги прямо пропорциональна её градусной
17.
18. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 большедругой.
Решение.
Площадь прямоугольника равна произведению его сторон. Найдём стороны прямоугольника.
Пусть x — меньшая сторона прямоугольника, тогда другая сторона равна
Следовательно,
периметр прямоугольника равен
откуда
О т в е т : 204.
Поэтому площадь прямоугольника равна
18.
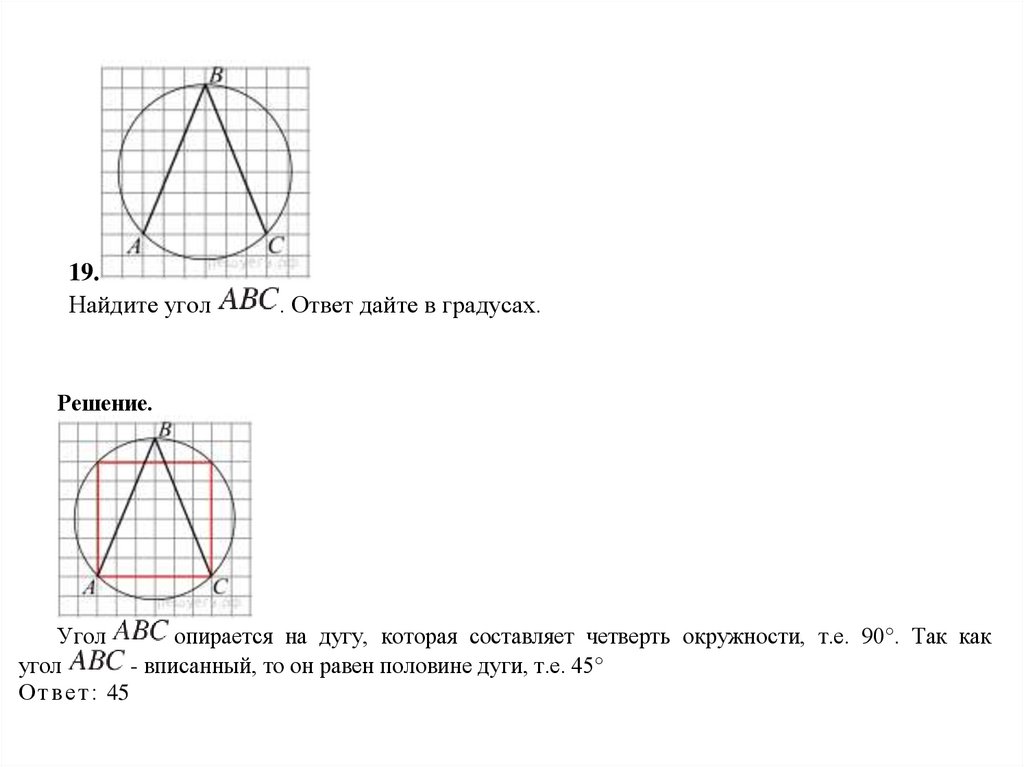
19.Найдите угол
. Ответ дайте в градусах.
Решение.
Угол
опирается на дугу, которая составляет четверть окружности, т.е. 90°. Так как
угол
- вписанный, то он равен половине дуги, т.е. 45°
О т в е т : 45
19.
20. Какое из следующих утверждений верно?1) Диагонали параллелограмма равны.
2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу
другого треугольника, то такие треугольники равны.
Если утверждений несколько, запишите их номера в порядке возрастания.
Решение.
Проверим каждое из утверждений.
1) «Диагонали параллелограмма равны» — неверно, если в параллелограмме диагонали равны,
то этот параллелограмм — прямоугольник, т. е. не у каждого параллелограмма диагонали равны.
2) «Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.»
— верно, ромб — частный случай параллелограмма, а площадь параллелограмма равна a · h.
3) «Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу
другого треугольника, то такие треугольники равны» — неверно, нет такого признака равенства
треугольников.
О т в е т : 2.
20.
21. Решите систему уравнений:Решение.
Вычтем из первого уравнения второе и получим соотношение:
Подставив полученное выражение в первое уравнение системы, получаем
Таким образом, искомым решением являются точки:
О т в е т : (0;0), (0,5;0,5)
и
21.
22. Первая труба пропускает на 2 литраводы в минуту меньше, чем вторая. Сколько
литров воды в минуту пропускает вторая
труба, если резервуар объёмом 130 литров
она заполняет на 4 минуты быстрее, чем
первая труба заполняет резервуар объёмом
136 литров?
22.
Решение.Пусть вторая труба пропускает
пропускает
литра в минуту.
литров воды в минуту,
, тогда первая труба
Составим таблицу по данным задачи:
Производительность
Время (мин) Объём работ (л)
(л/мин)
Первая труба
136
Вторая труба
130
Так как вторая труба заполнила резервуар на 4 минуты быстрее, получаем уравнение:
Решим уравнение:
или
Отбрасывая постороннее решение −6,5, получаем, что вторая труба пропускает 10 литров в
минуту.
О т в е т : 10.
23.
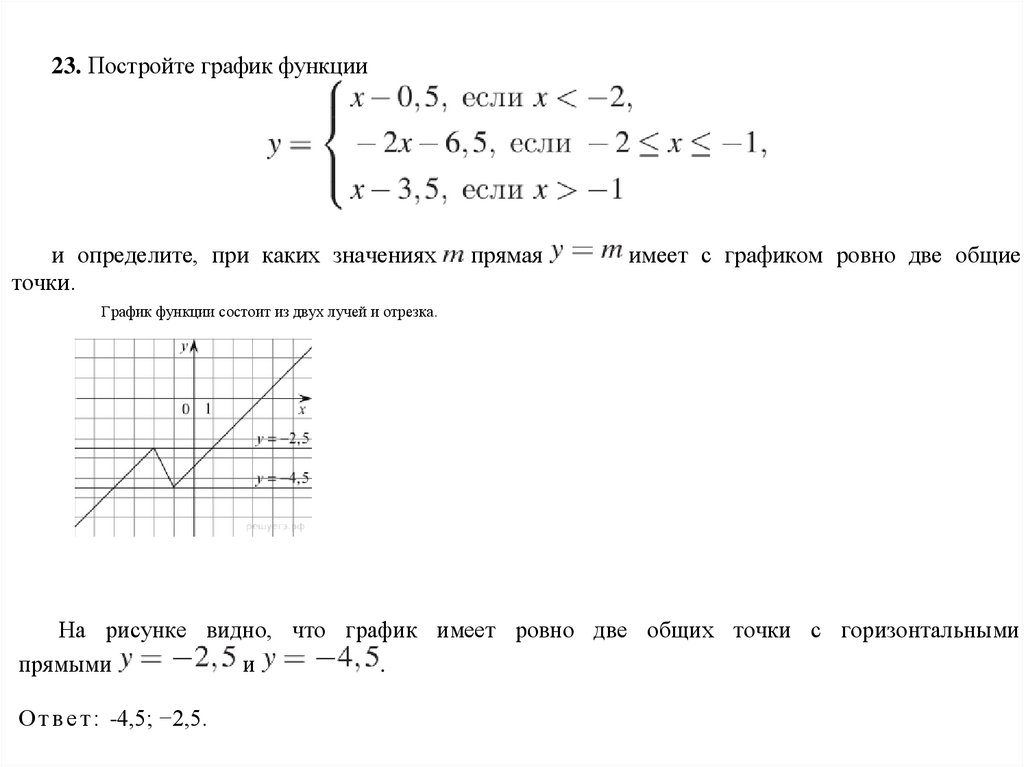
23. Постройте график функциии определите, при каких значениях
точки.
прямая
имеет с графиком ровно две общие
График функции состоит из двух лучей и отрезка.
На рисунке видно, что график имеет ровно две общих точки с горизонтальными
прямыми
и
.
О т в е т : -4,5; −2,5.
24.
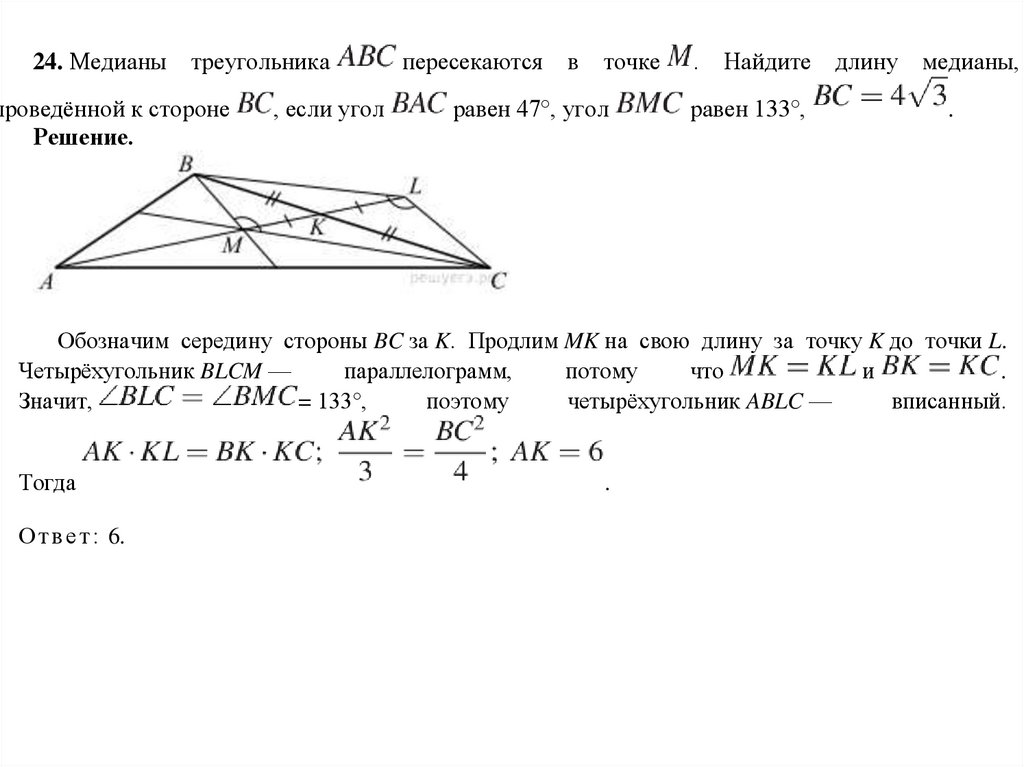
24. Медианы треугольникапроведённой к стороне
Решение.
, если угол
пересекаются
в точке
равен 47°, угол
.
Найдите длину медианы,
равен 133°,
.
Обозначим середину стороны BC за K. Продлим MK на свою длину за точку K до точки L.
Четырёхугольник BLCM —
параллелограмм,
потому
что
и
.
Значит,
= 133°,
поэтому
четырёхугольник ABLC —
вписанный.
Тогда
О т в е т : 6.
.
25.
25. В параллелограмме ABCD проведенывысоты BH и BE к сторонам AD и CD
соответственно, при этом BH = BE. Докажите,
что ABCD — ромб.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой
стороне.
Тогда, с одной стороны, S = AD · BH, а с другой стороны, S = CD · BE. Поскольку BH = BE ,
получаем, что AD = CD. Следовательно, все стороны параллелограмма равны, а значит, ABCD —
ромб.


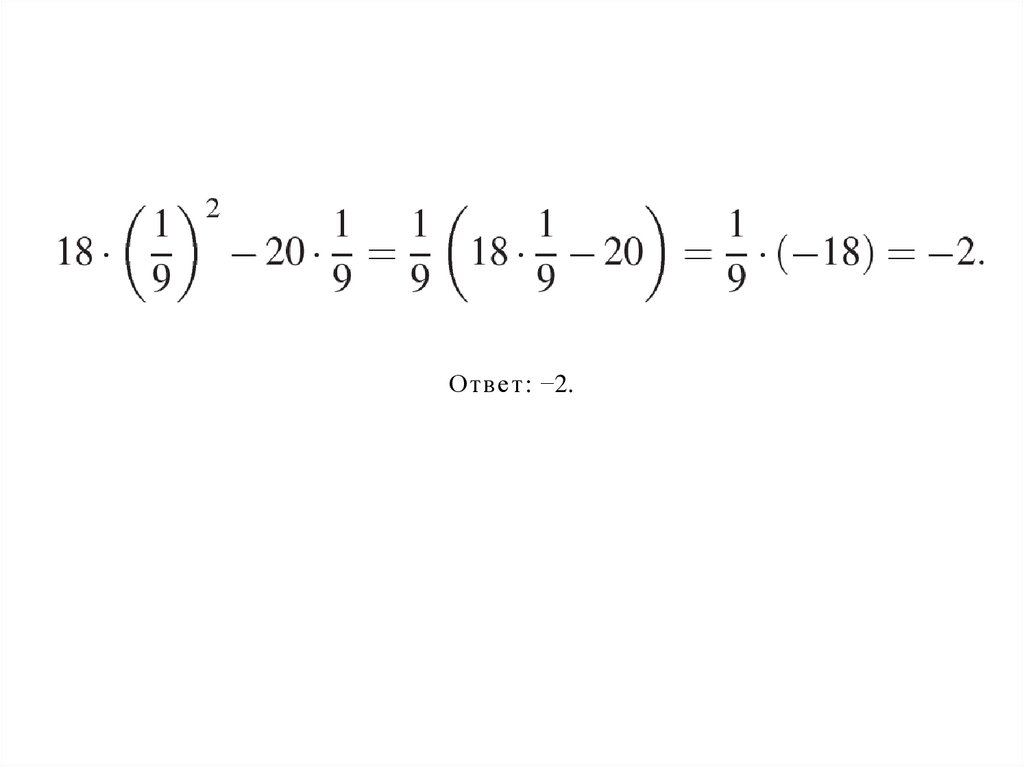

















 Математика
Математика








