Площадь параллелограмма

1.

ha
а
Урок геометрии
в 8 классе по теме
«Площадь параллелограмма»
Выполнила: учитель математики МБОУ «КСОШ
им. Т. Т. Шерета» Шевченко И. В.

2.

Цель урока: вывести формулу для вычисления площади параллелограмма и
использовать её при решении задач
Задачи:
- обучающие
Развивать логического мышление и интеллектуальные навыки в ходе
вывода формулы;
показать применение этой формулы в процессе решения задач;
совершенствовать навыки решения задач;
совершенствовать навыки работы с чертежными инструментами;
- развивающие
развивать умения анализировать, сравнивать, обобщать, делать выводы.
- воспитательные
развивать положительный эффект от настойчивости при достижении цели;
способствовать пониманию необходимости интеллектуальных усилий для
успешного обучения;
воспитывать аккуратность, самостоятельность, интерес к предмету.

3.

Тип урока: комбинированный урок
Формы работы обучающихся:
фронтальная, индивидуальная, групповая.
Необходимое техническое оборудование:
компьютер, мультимедийный проектор,
демонстрационные чертёжные
принадлежности.

4.

Индивидуальная работа с заданиями
1. Назовите известные вам формулы площадей фигур.
2. Назовите формулу площади прямоугольника.
3. Назовите формулу площади квадрата.
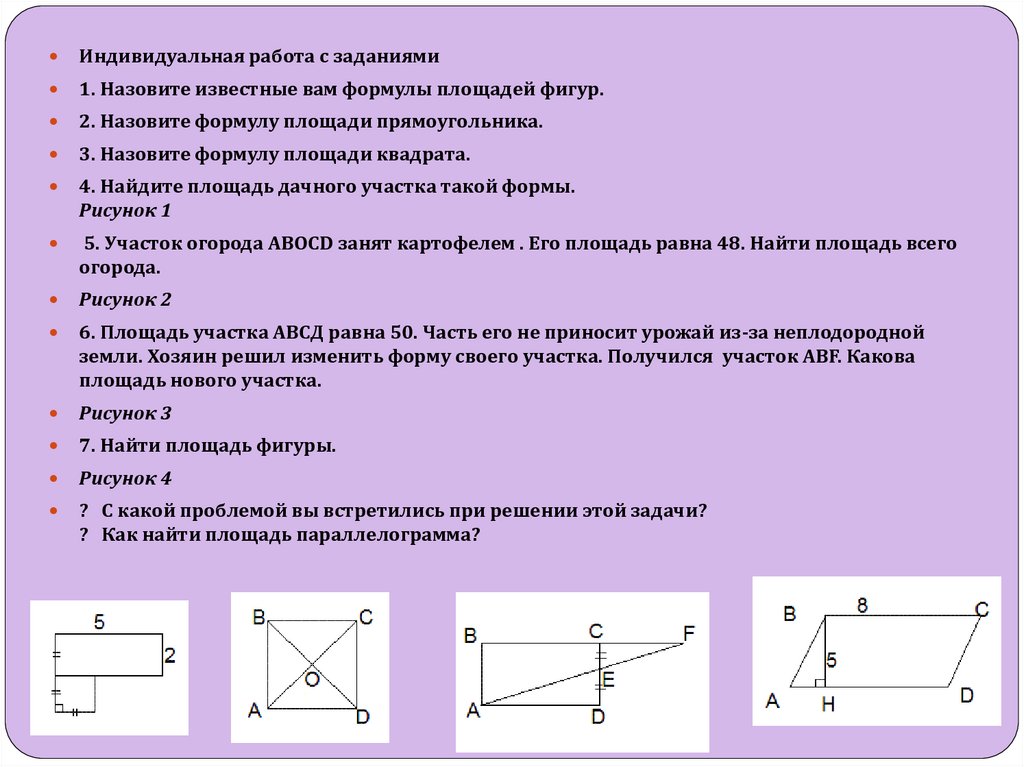
4. Найдите площадь дачного участка такой формы.
Рисунок 1
5. Участок огорода АВОСD занят картофелем . Его площадь равна 48. Найти площадь всего
огорода.
Рисунок 2
6. Площадь участка АВСД равна 50. Часть его не приносит урожай из-за неплодородной
земли. Хозяин решил изменить форму своего участка. Получился участок АВF. Какова
площадь нового участка.
Рисунок 3
7. Найти площадь фигуры.
Рисунок 4
? С какой проблемой вы встретились при решении этой задачи?
? Как найти площадь параллелограмма?

5.

Теорема.
Площадь параллелограмма равна произведению длины стороны
параллелограмма на высоту, проведенную к этой стороне.
Дано: АВСD – параллелограмм, ВН – высота
Доказать: S(ABCD )= AD · BH
Доказательство: проведем еще одну высоту
параллелограмма – отрезок СК и рассмотрим
треугольники АВН и DСК. Они прямоугольные и
равны по гипотенузе и катету (гипотенузы АВ и
СD равны как противоположные стороны
параллелограмма, катеты ВН и СК равны как
расстояния между параллельными прямыми).
Значит, площади треугольников равны.
S(ABCD)=S(ABH)+S(HBCD)
S(HBCK ) = S(HBCD)+S(DCK), S(ABH)= S(DCK)→ S(ABCD)=S(HBCK)
S(HBCK )= HK · BH, так как НВСК – прямоугольник;
так как AD = BC = HK, то S(ABCD )= HK · BH = AD · BH .
Итак, S(ABCD )= AD · BH .
Теорема доказана.

6.

7.

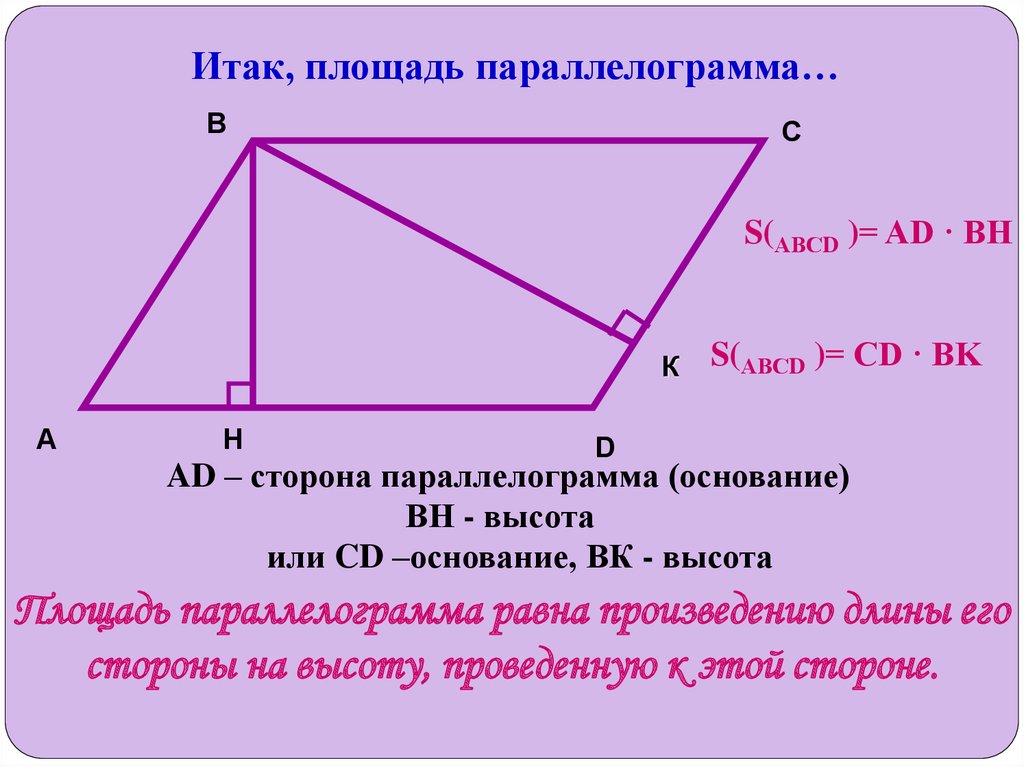
Итак, площадь параллелограмма…
B
C
S(АВСD )= AD · BH
К
A
H
S(АВСD )= CD · BK
D
AD – сторона параллелограмма (основание)
ВН - высота
или CD –основание, ВК - высота
Площадь параллелограмма равна произведению длины его
стороны на высоту, проведенную к этой стороне.

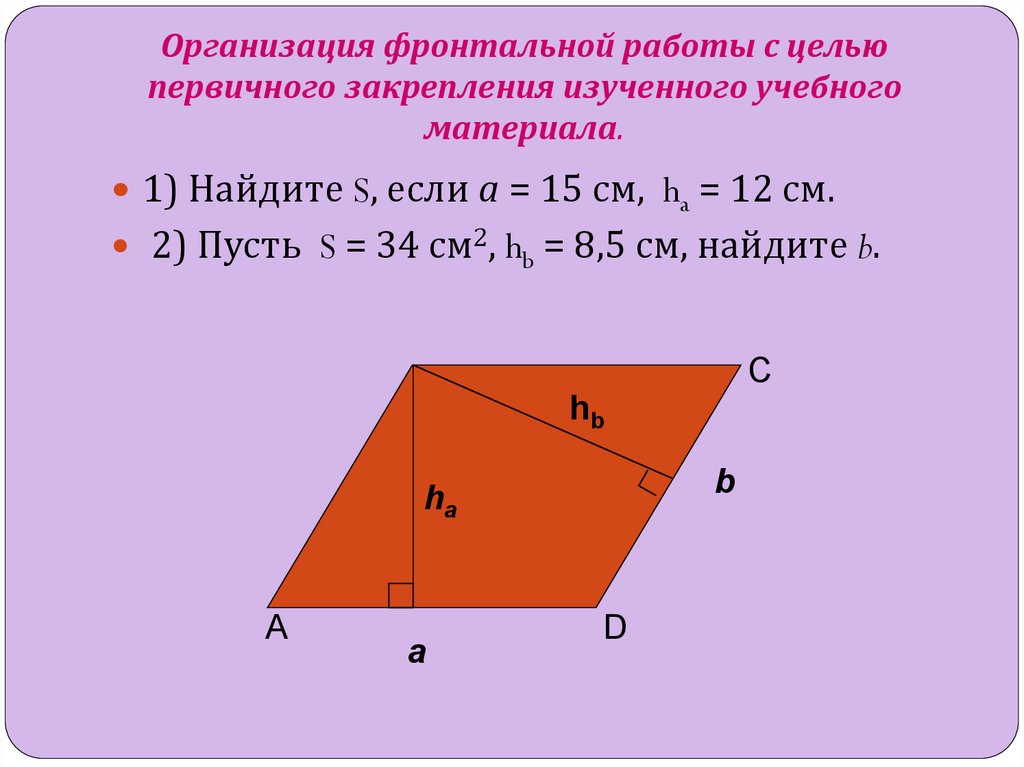
8. Организация фронтальной работы с целью первичного закрепления изученного учебного материала.

1) Найдите S, если а = 15 см, ha = 12 см.
2) Пусть S = 34 см2, hb = 8,5 см, найдите b.
С
hb
b
ha
А
а
D

9. Выполнение обучающей самостоятельной работы

Вариант 1
1. Стороны параллелограмма равны 10 см и 6 см, а угол между
этими сторонами равен 150 0. Найдите площадь этого
параллелограмма.
2. В параллелограмме АВСД стороны равны 14 и 8 см, высота,
проведенная к большей стороне, равна 4 см. Найдите площадь
параллелограмма и вторую высоту.
Вариант 2
Острый угол параллелограмма равен 300, а высоты,
проведенные из вершины тупого угла, равны 4 см и 3 см.
Найдите площадь этого параллелограмма.
2. В параллелограмме АВСД высоты равны 10 и 5 см, а площадь
параллелограмма равна 60см². Найдите стороны
параллелограмма

10.

Домашнее задание:
п.51, теорема о площади параллелограмма,
№ 459(в, г), № 465
Дополнительная задача : В параллелограмме
АВСD диагональ ВD перпендикулярна стороне
АВ и равна 5 см. Сторона АD равна 8 см, ∠ВАD
равен 60º. Найдите площадь параллелограмма.