Похожие презентации:
Производная. Реши ребус
1. Здравствуйте, студенты! Урок «открытия» знания
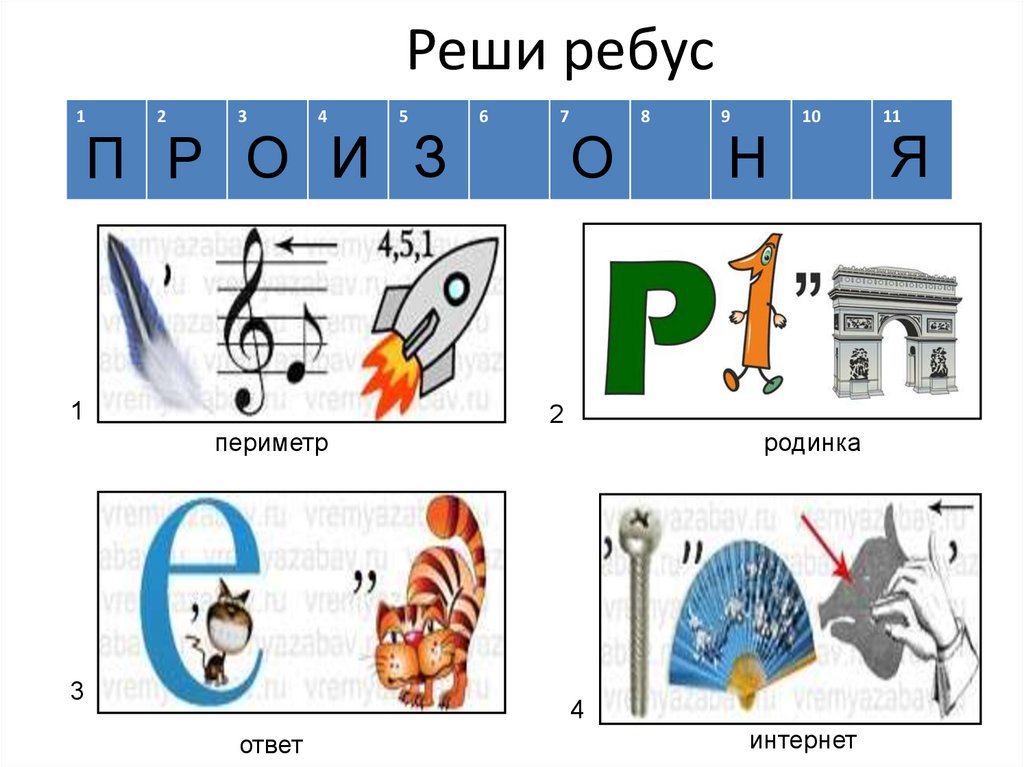
2. Реши ребус
12
3
4
5
П Р О И З
1
1
1
6
7
О
8
9
Н
10
1
1
2
периметр
1
1
3
родинка
1
1
4
ответ
интернет
11
Я
3.
12
3
4
5
6
7
8
9
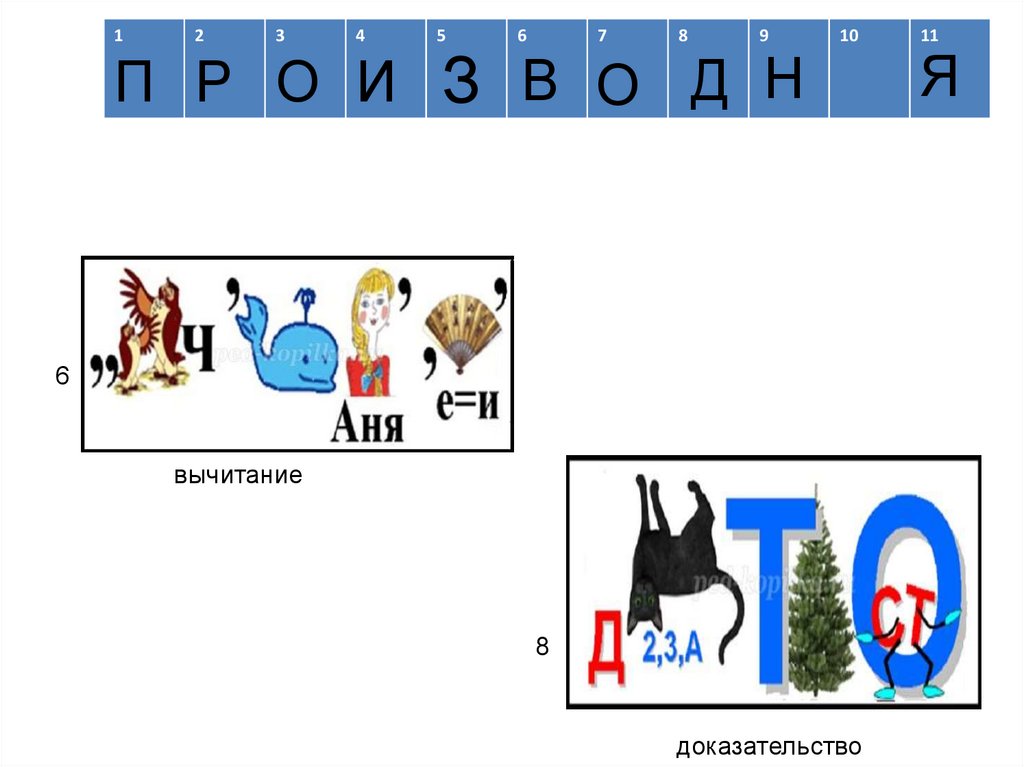
П Р О И З В О Д Н
10
56
вычитание
58
доказательство
11
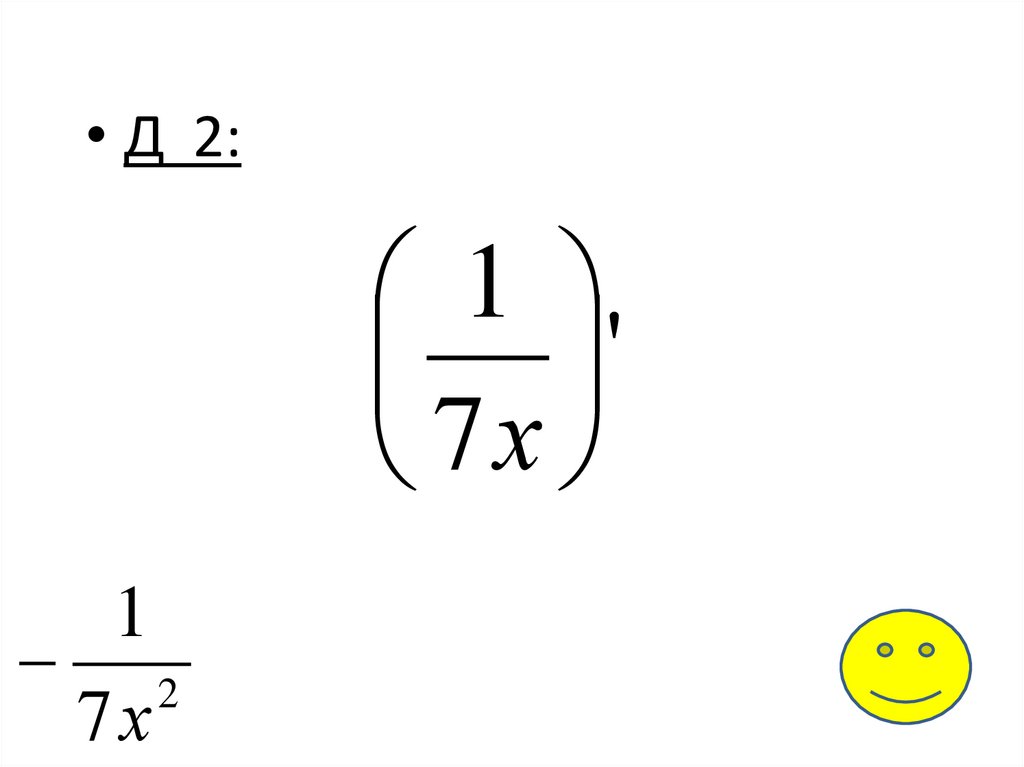
Я
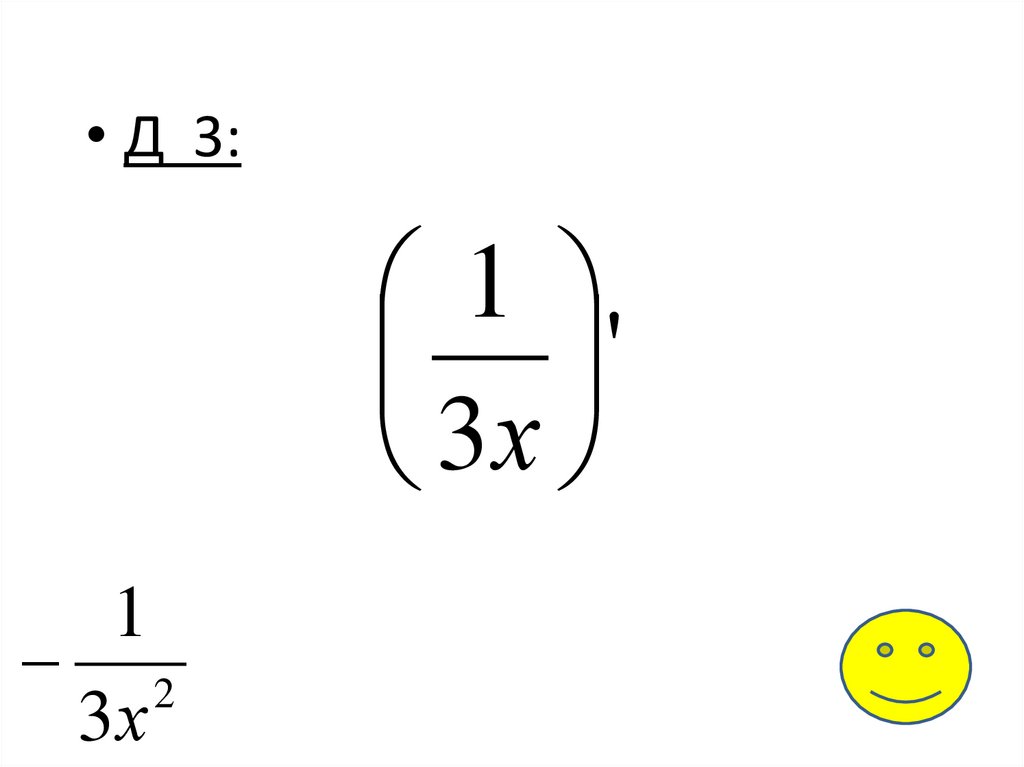
4.
12
3
4
5
6
7
8
9
10
11
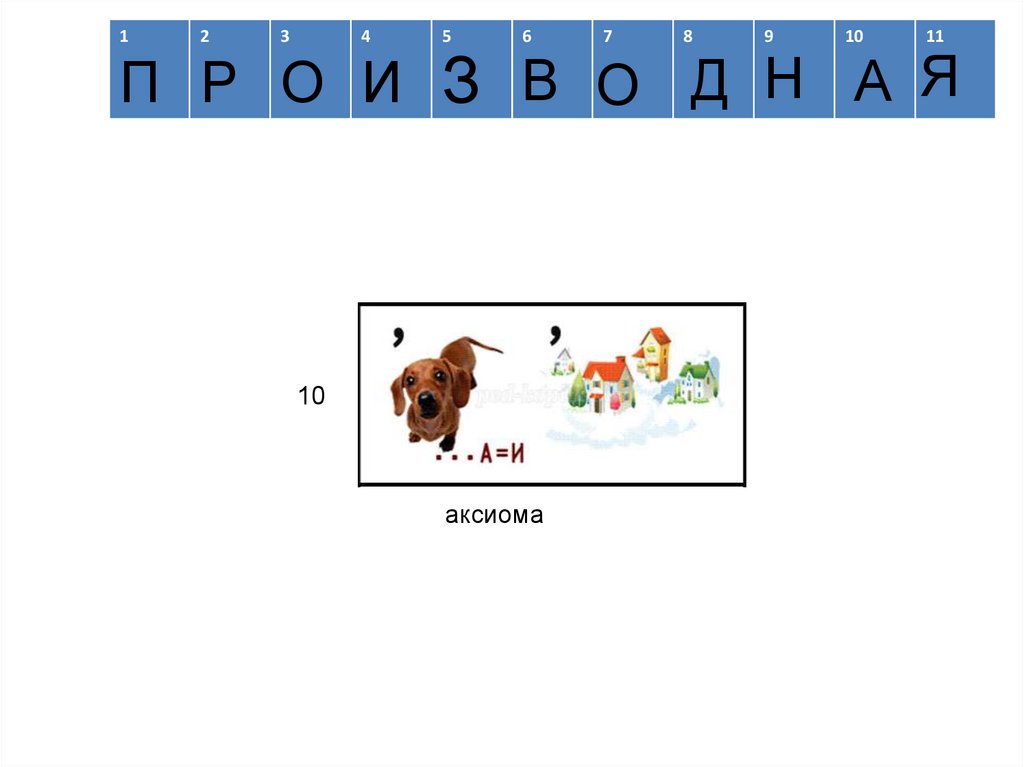
П Р О И З В О Д Н А Я
10
аксиома
5.
Тема: «Производная иправила ее вычисления»
Цель урока: изучить основные формулы и правила
дифференцирования, научиться применять теорию на
практике
6. «Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям
действительного мира»Никола́й Ива́нович Лобаче́вский —
русский математик, один из создателей
неевклидовой геометрии, деятель
университетского образования и народного
просвещения.
7. «А зачем нам изучать её? Пригодятся ли полученные знания по нахождению производных в жизни?»
8.
Применение производной в математикеПроизводная в математике показывает числовое выражение
степени изменений величины, находящейся в одной и тоже
точке, под влиянием различных условий.
Формула производной встречается нам ещё в 15 веке. Великий
итальянский математик Тартальи, рассматривая и развивая
вопрос - на сколько зависит дальность полёта снаряда от
наклона орудия - применяет её в своих трудах.
Формула производной часто встречается в работах известных
математиков 17 века. Её применяли Ньютон и Лейбниц.
9. Д/З
• Сделать презентацию на следующие темы:1). Применение производной в биологии.
2). Применение производной в физике.
3). Применение производной в повседневной
жизни.
Презентация должна содержать 8-10 слайдов,
включая: титульный слайд, материал, заключение,
список литературы (интернет ресурсы).
• Выучить таблицу производных и теоремы
дифференцирования, подготовиться к
математическому диктанту.
10. Экскурс в историю
ЭКСКУРС В ИСТОРИЮПроизводная – одно из фундаментальных понятий
математики, характеризующее скорость изменения
функции в данной точке.
Понятие производной возникло в связи с
необходимостью решения ряда задач из физики,
механики и математики, но в первую очередь
следующих
двух:
определение
скорости
прямолинейного
движения
и
построения
касательной к прямой.
Независимо друг от друга Исаак Ньютон и
Готфрид
Лейбниц
разработали
теорию
дифференциального исчисления.
11.
12.
13.
14.
15.
16.
Теоретическийматериал по теме
«ПРОИЗВОДНАЯ»
17.
Производные - это такие функции, которые получаются иззаданных
функций
путем
вычисления
предела
разностного отношения. Разностным отношением
называется отношение разности значения функции к
разности значений переменной.
Возникает вопрос? Почему производная есть тоже функция?
Дело в том, что предел функции мы можем вычислить
только в точке, а значение предела есть число f'(x0).
Но если менять это число x0, то f'(x0) будет тоже функцией от
x0.
18. Как найти производную?
1. Необходимо знать таблицу производных основныхэлементарных функций.
2. Уметь видеть, как составная функция строится из
основных элементарных функций.
3. Знать формулы производной составных функций – то
есть
производных
суммы,
произведения
функции и частного сложной функции.
сложной
19. Таблица производных
20. Правила дифференцирования
21. Теорема 1
Производная суммы любого числафункций равна сумме производных
этих функций.
Для трех функций, например, имеем:
22. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ ПРОСТЫХ ФУНКЦИЙ
Пример 1.1Пример 1.2
23. Теорема 2
Производная произведениядвух функций равна
24. Пример 2.1
25. Теорема 3
Производная частногодвух функций равна
26. Найти производную функции
Пример 3.1Найти производную функции
27.
“Ум заключается нетолько в знании,
но и в умении
применять знания на
практике”
Аристотель
28.
Конкурспрактиков
1
2
3
4
5
=А= (1 б.)
=1=
=2=
=3=
=4=
=5=
=Б= (2 б.)
=1=
=2=
=3=
=4=
=5=
=В= (3 б.)
=1=
=2=
=3=
=4=
=5=
=Г= (4 б.)
=1=
=2=
=3=
=4=
=5=
=Д= (5 б.)
=1=
=2=
=3=
=4=
=5=
29.
• А 1:3 '
(5 x )
15x
2
30.
• Б 1:4x 2x
'
2
4 4х
31.
• В 1:(cos x sin x)
sin x cos x
'
32.
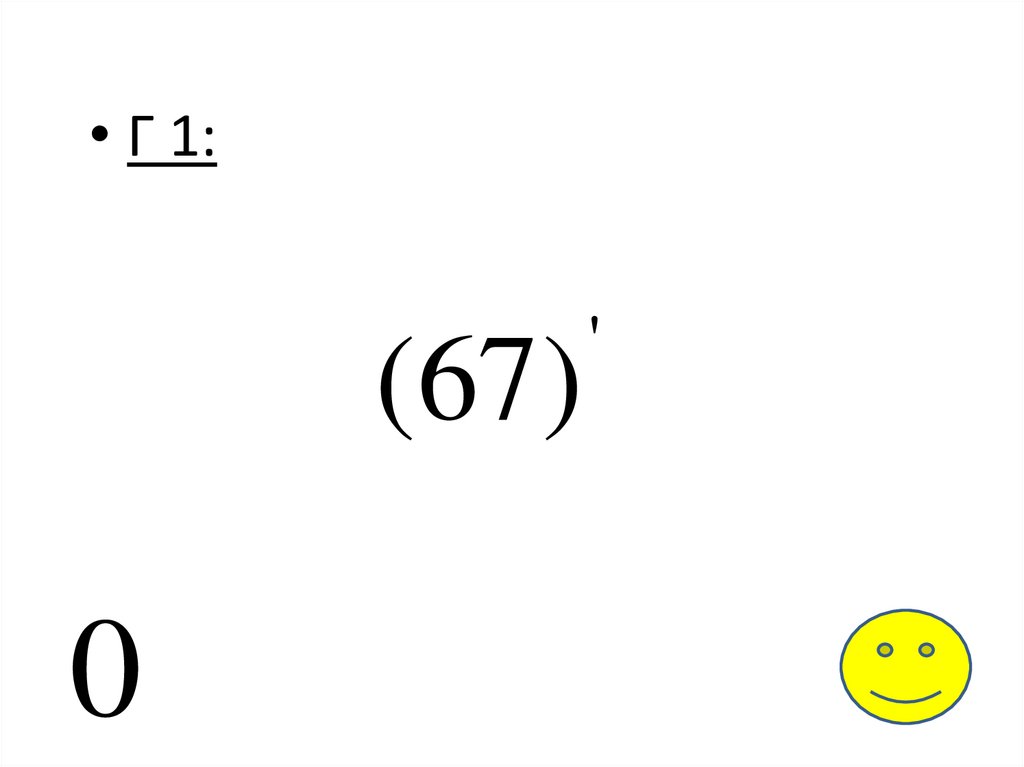
• Г 1:(67)
0
'
33.
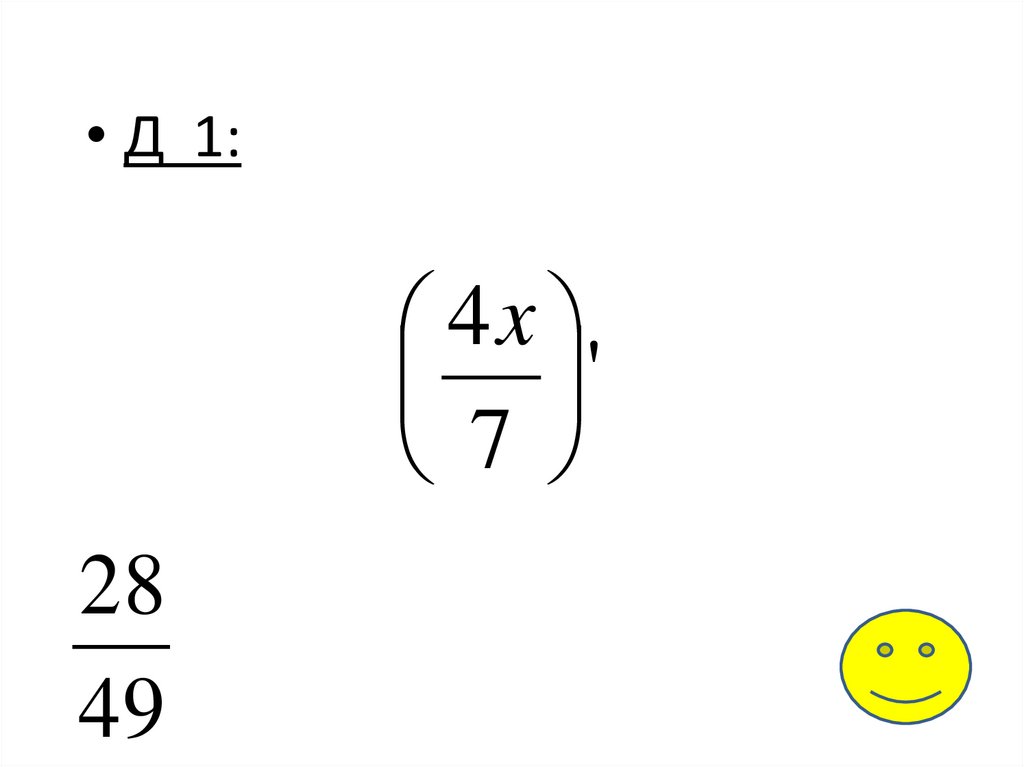
• Д 1:4x
'
7
28
49
34.
• А 2:(6 x )
6
'
35.
• А 3:(sin x)
cos x
'
36.
• А 4:(cos x)
sin x
'
37.
• А 5:2 '
(4 x )
8х
38.
• Б 2:3 4х
3x 2 x
'
2
39.
• Б 3:6 x 3x
'
3
6 9х
2
40.
• Б 4:4x 2x
'
2
4 4х
41.
• Б 5:2 x 4 x
3
6 х 8х
2
'
2
42.
• В 2:(2 х 4)
2
'
43.
• В 3:(2 х 40)
3
6х
2
'
44.
• В 4:(13 5х )
2 '
10 х
45.
• В 5:(20 2 х )
3 '
6х
2
46.
• Г 2:13 х '
(
)
2
1
6,5 (6 )
2
47.
• Г 3:1
3
х '
( )
3
48.
• Г 4:1
1,5 (1 )
2
3х '
( )
2
49.
• Г 5:8х '
( )
4
2
50.
• Д 2:1
'
7х
1
2
7х
51.
• Д 3:1
'
3х
1
2
3х
52.
• Д 4:74 '
0
53.
• Д 5:1
'
2х
1
2
2х
54. Подведение итогов
• я научился…• у меня получилось …
• я смог…
• я научился…
• я попробую…
• у меня получилось …
• меня удивило…
• я смог…
• урок дал мне для
• я попробую…
жизни…
• меня удивило…
• мне захотелось…
• урок дал мне для
жизни…
• мне захотелось…
























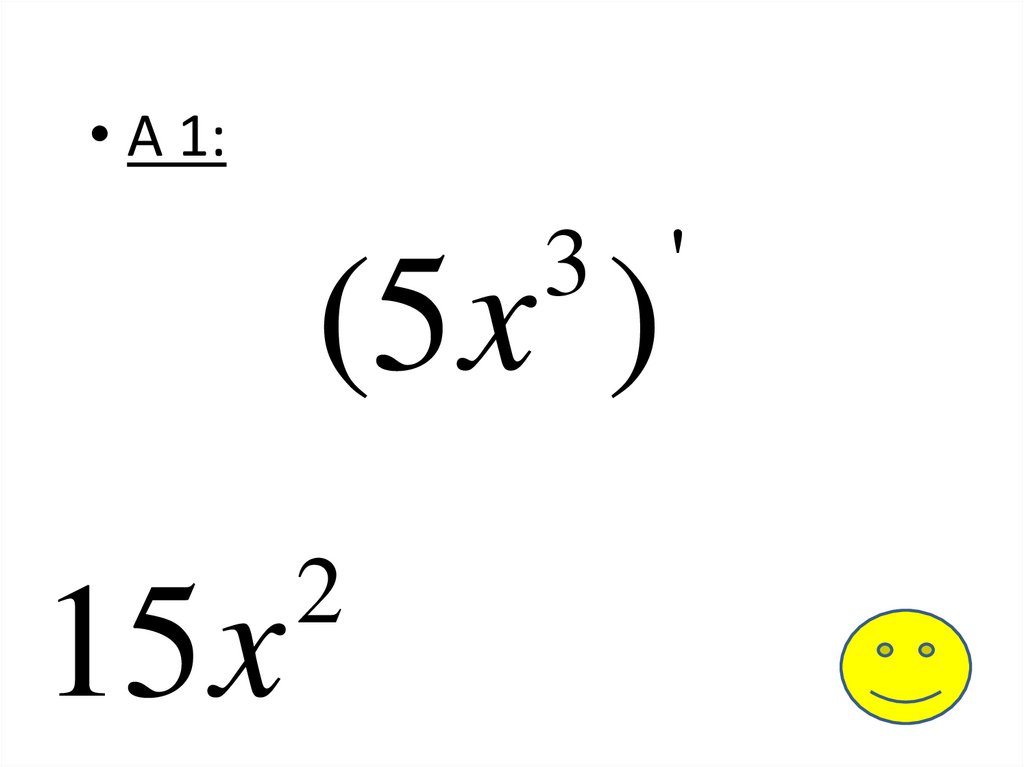
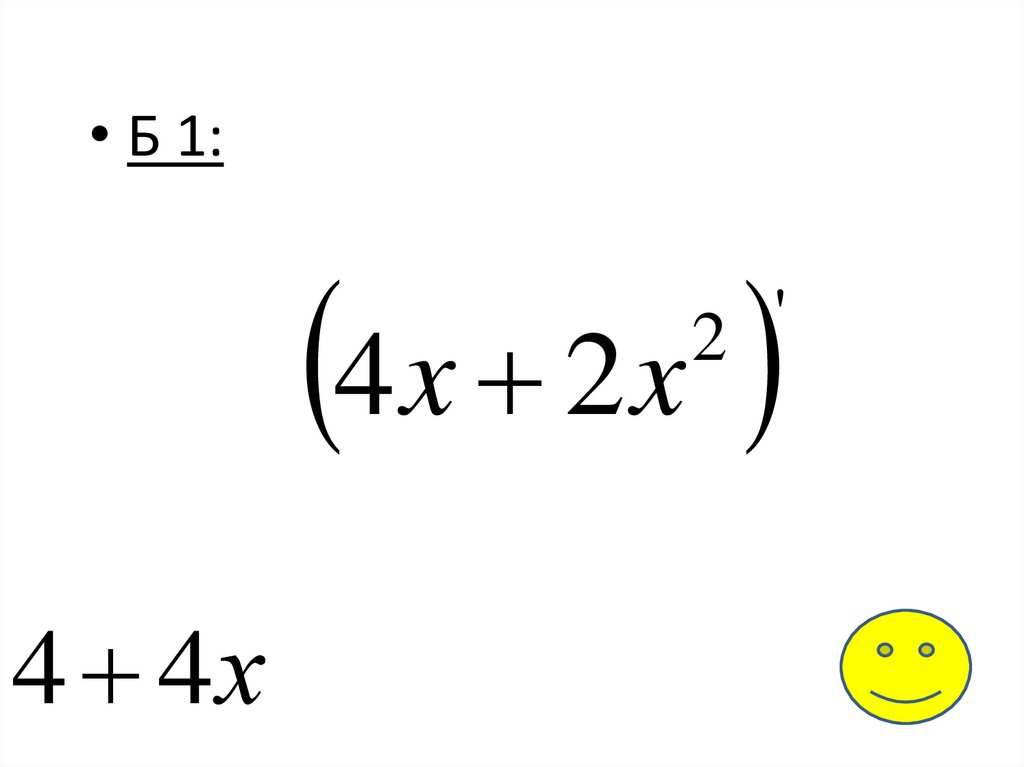
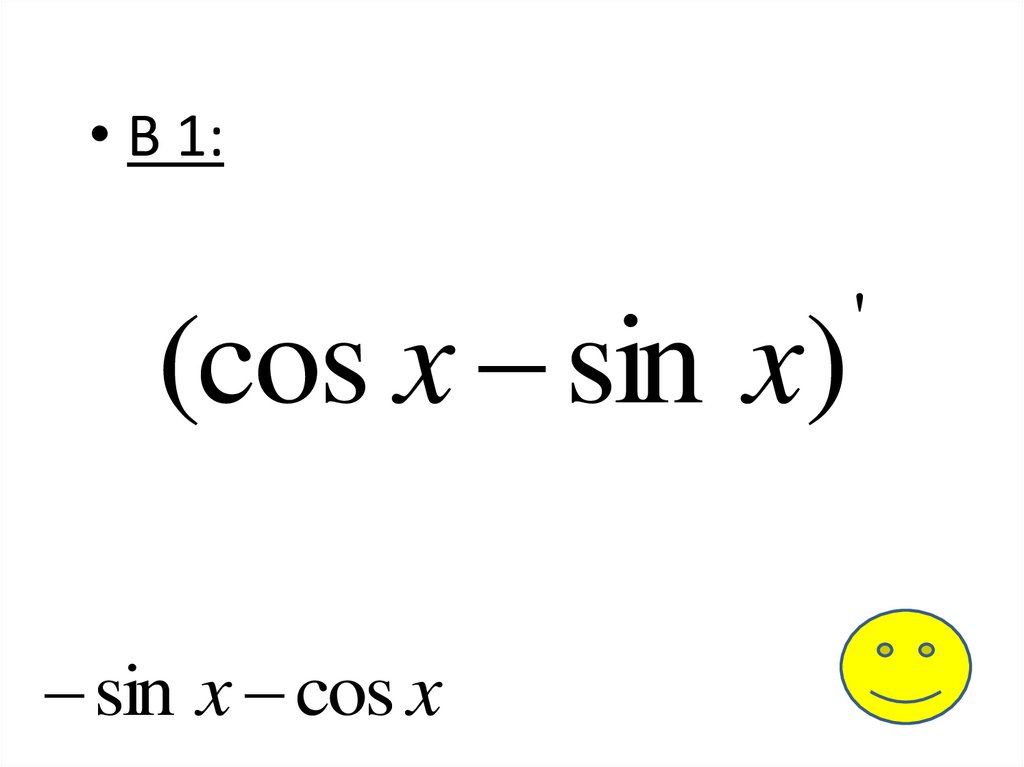

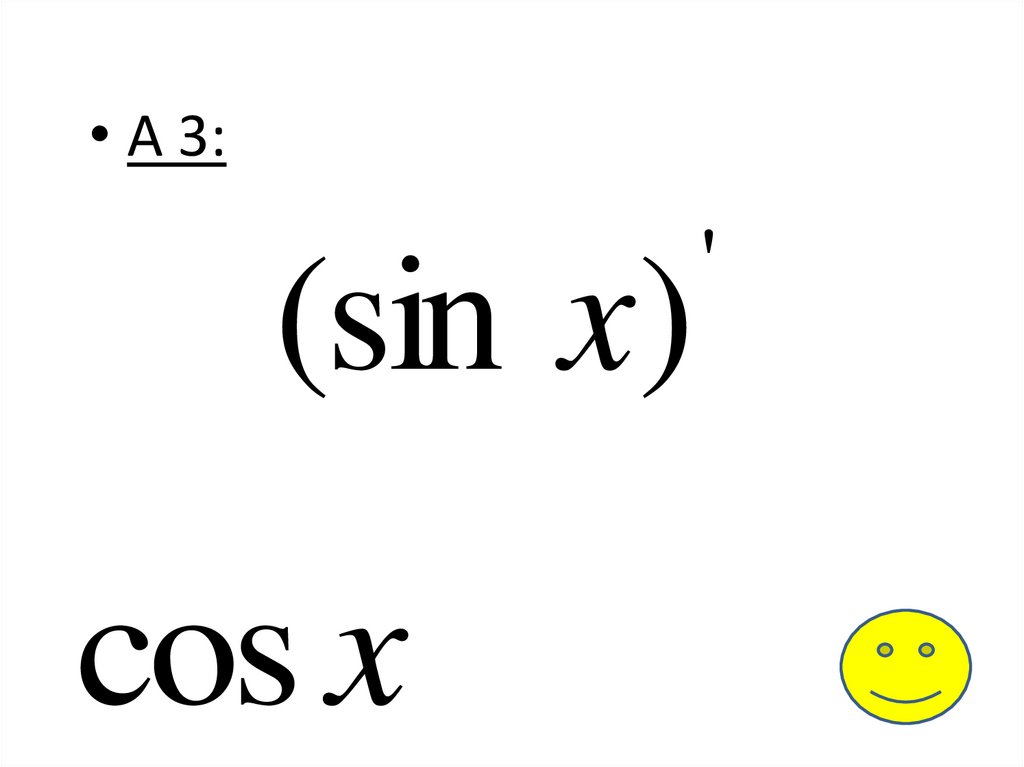
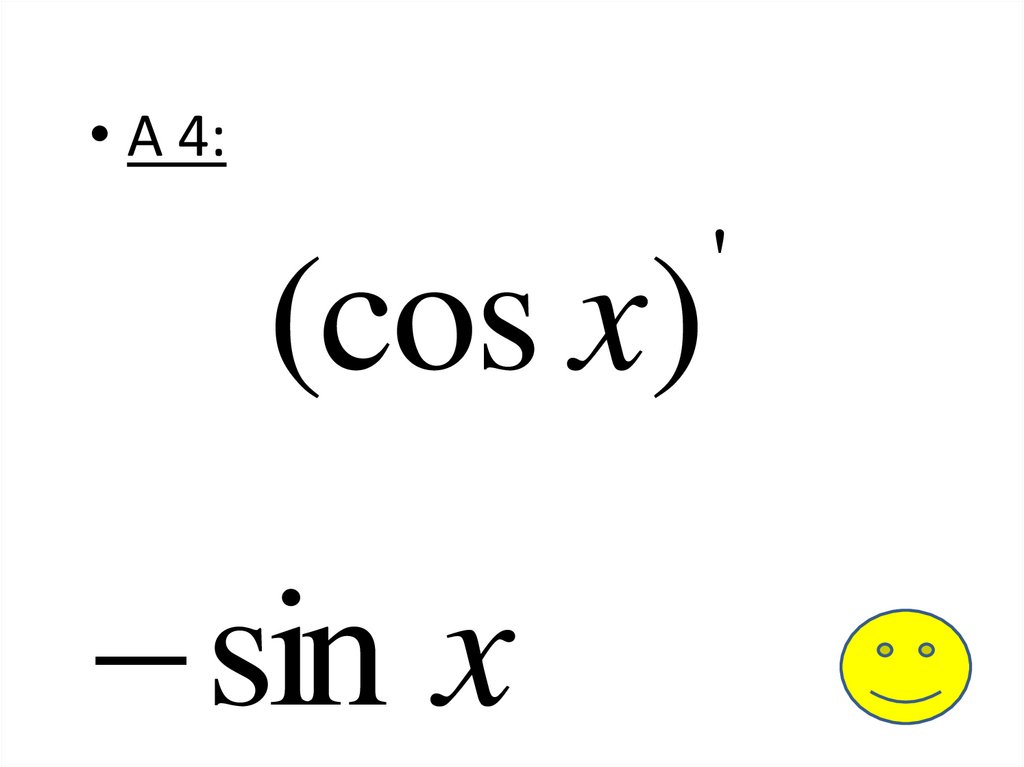
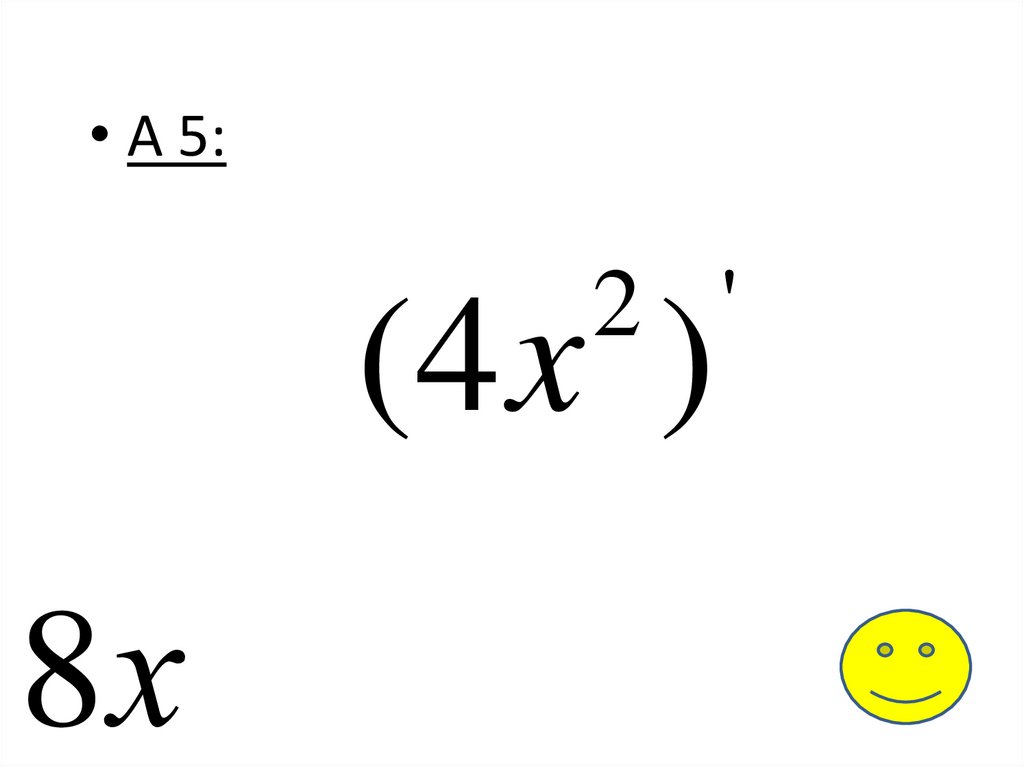
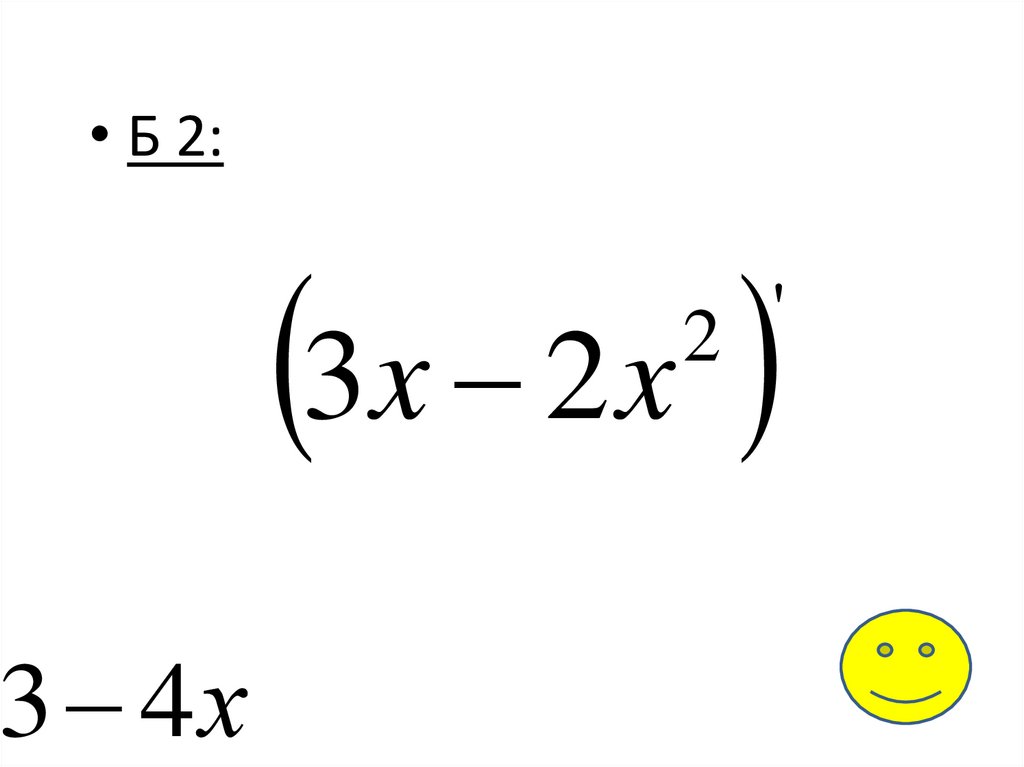
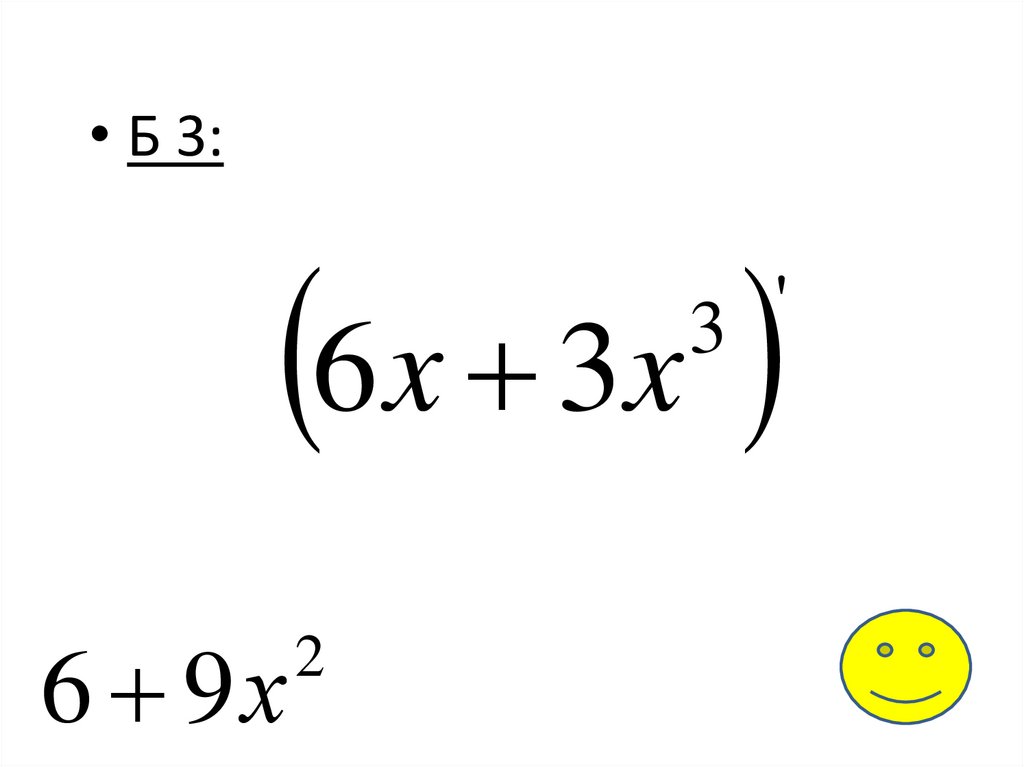
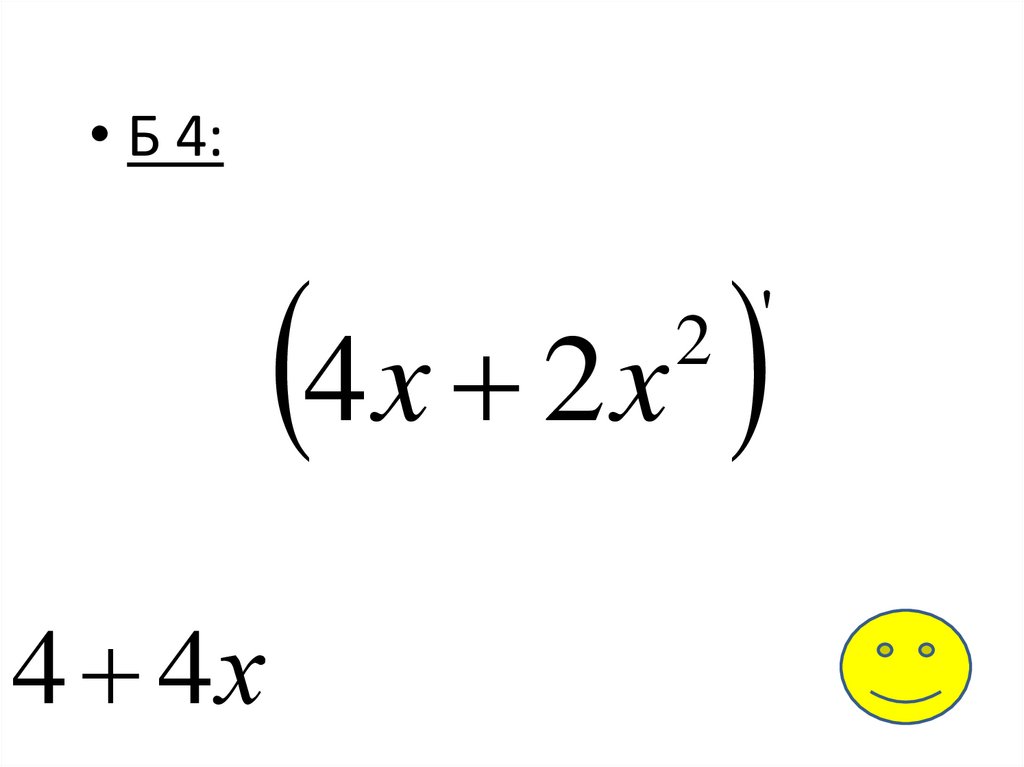
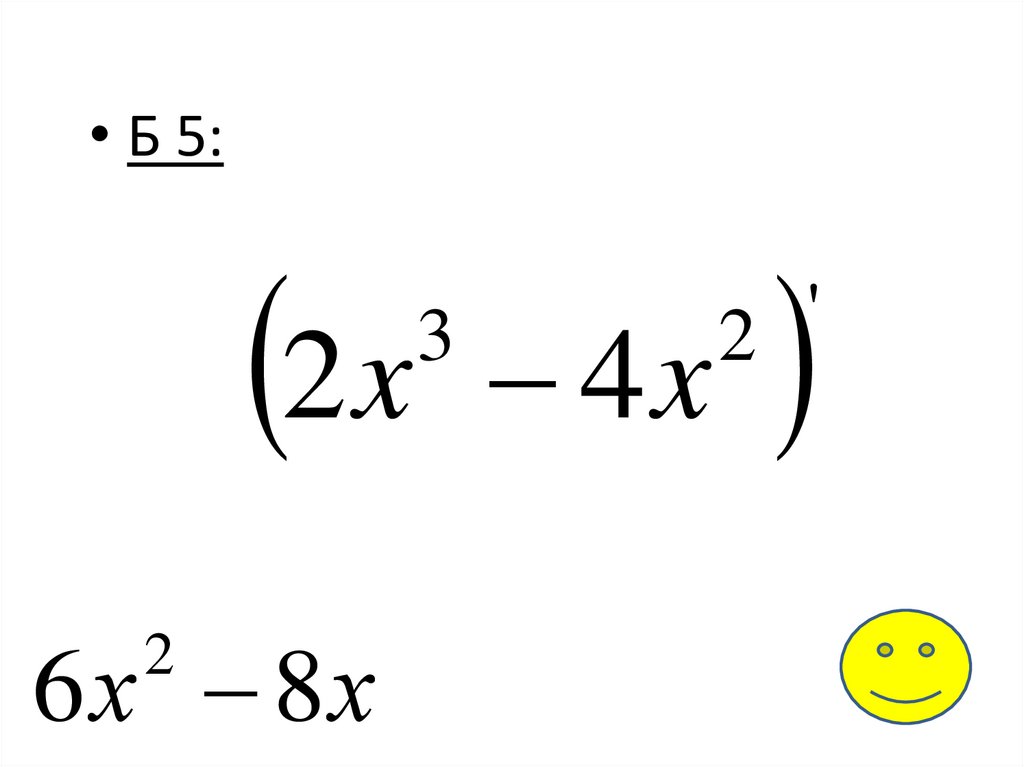
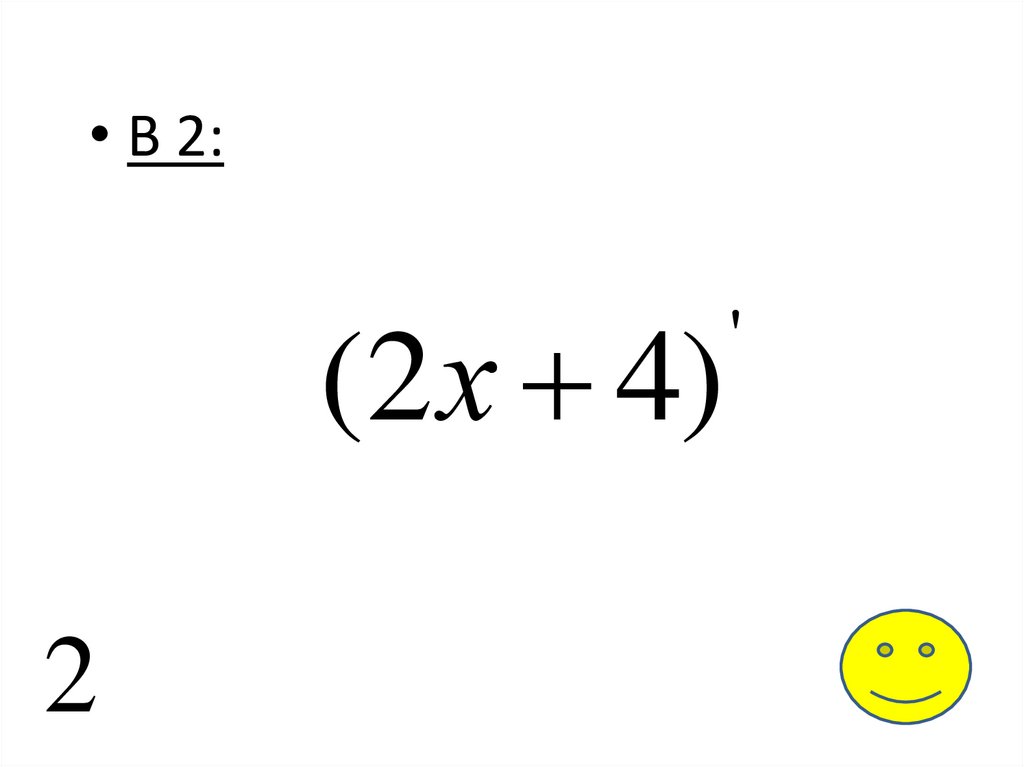

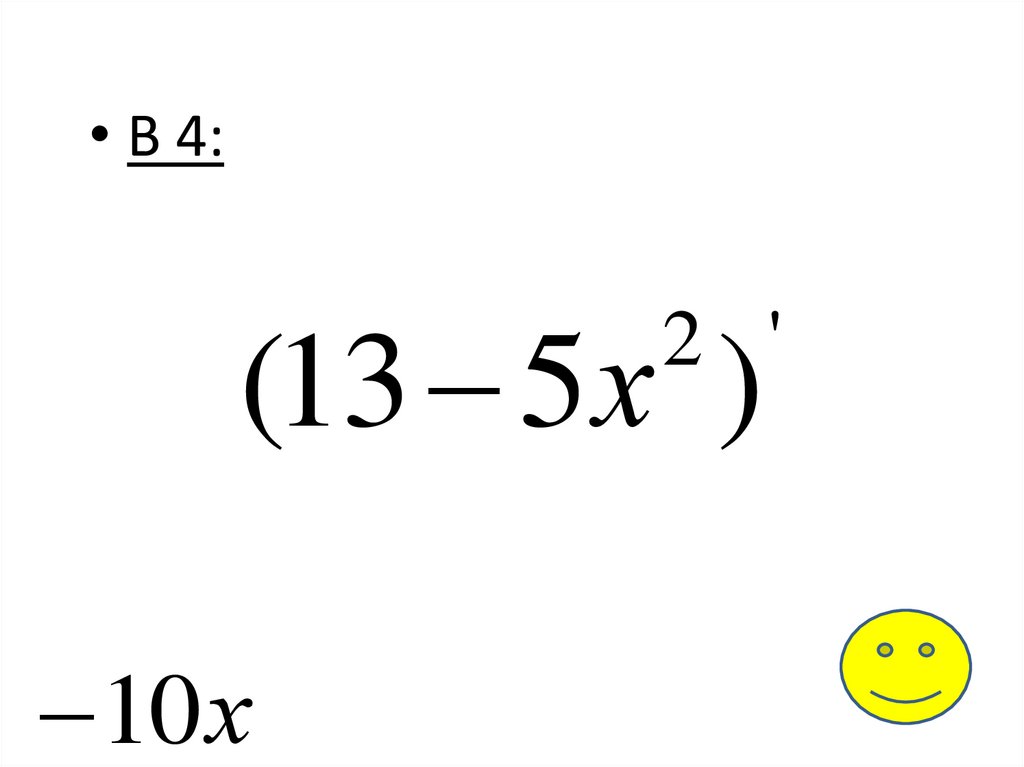
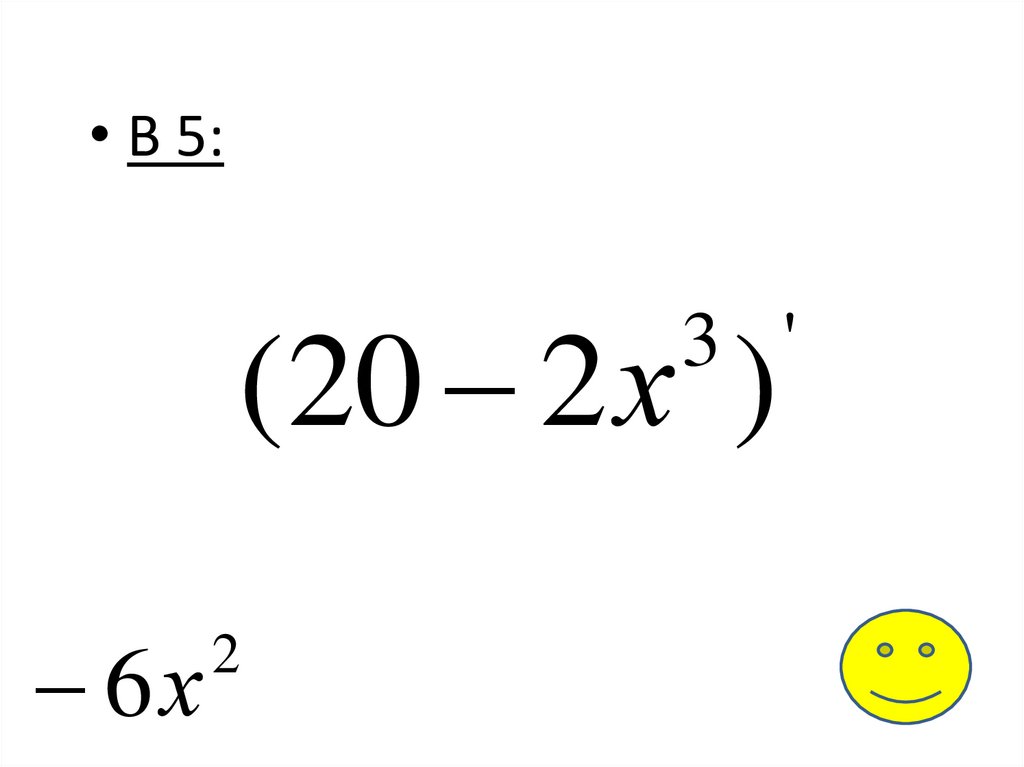
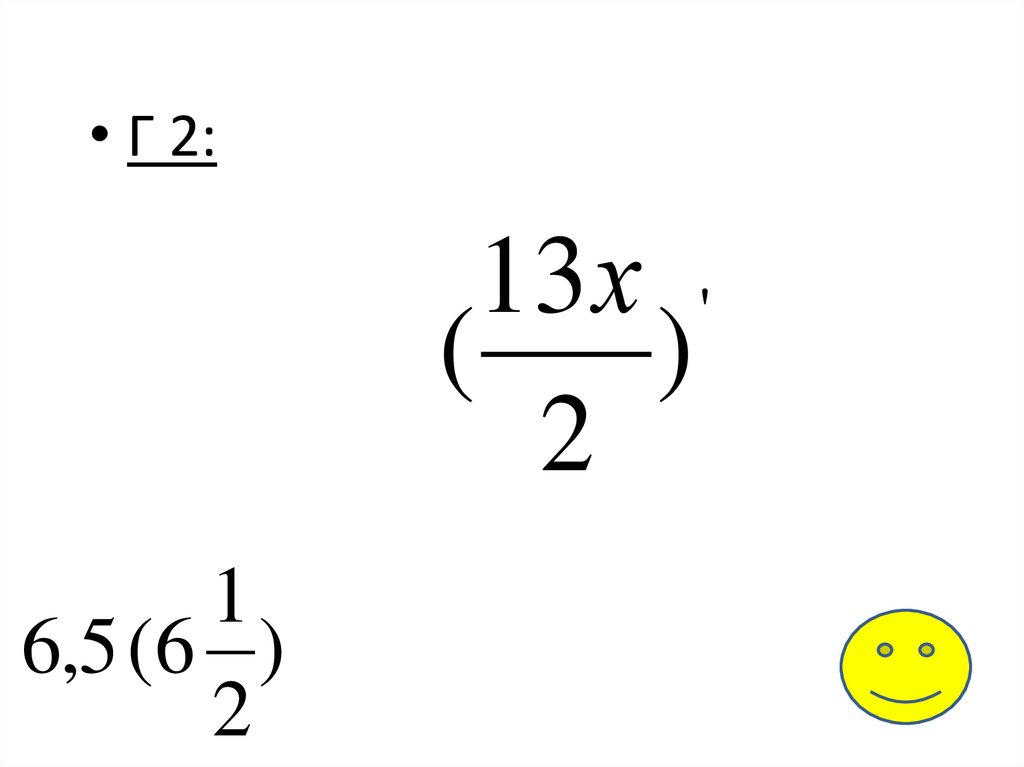

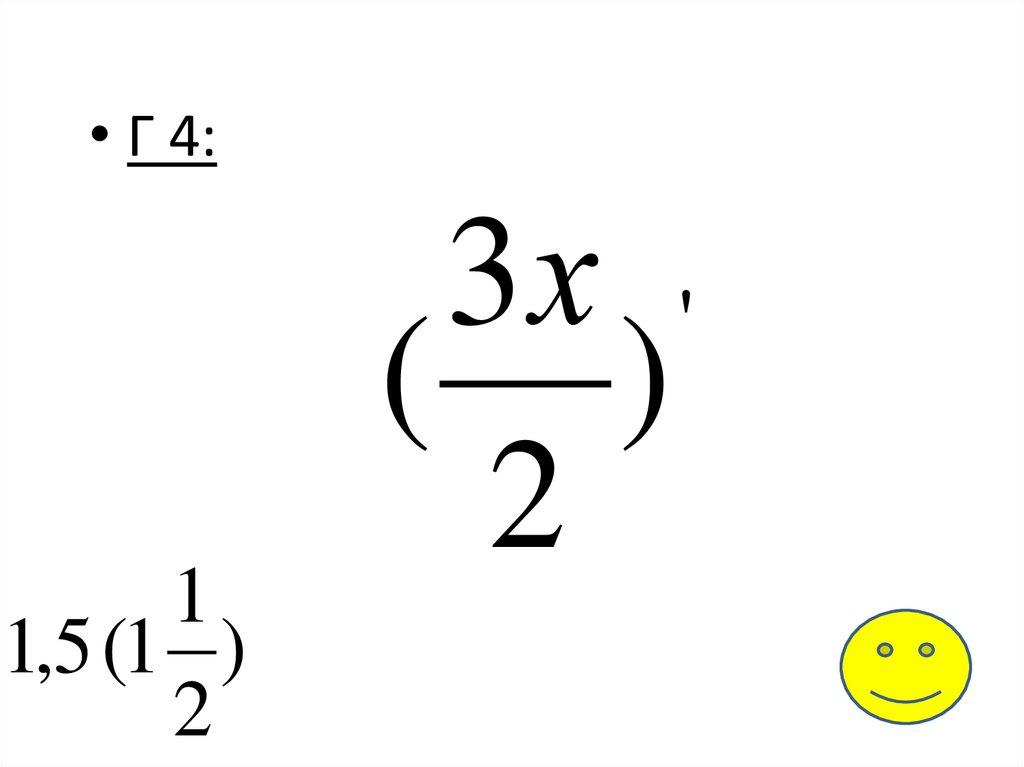
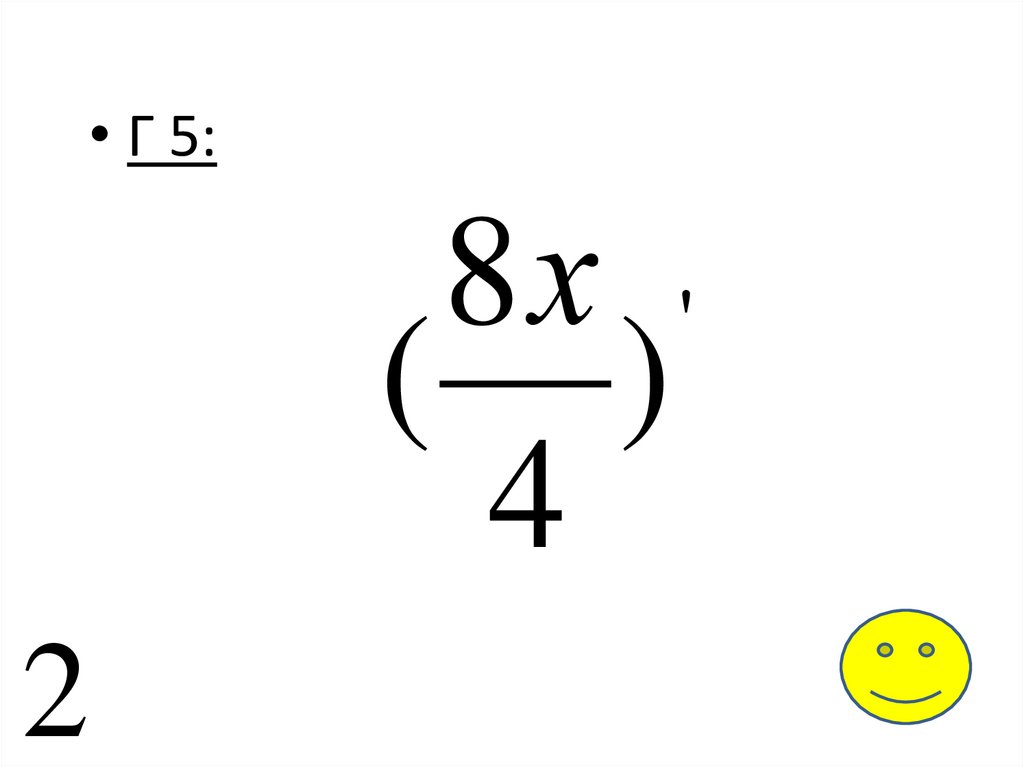

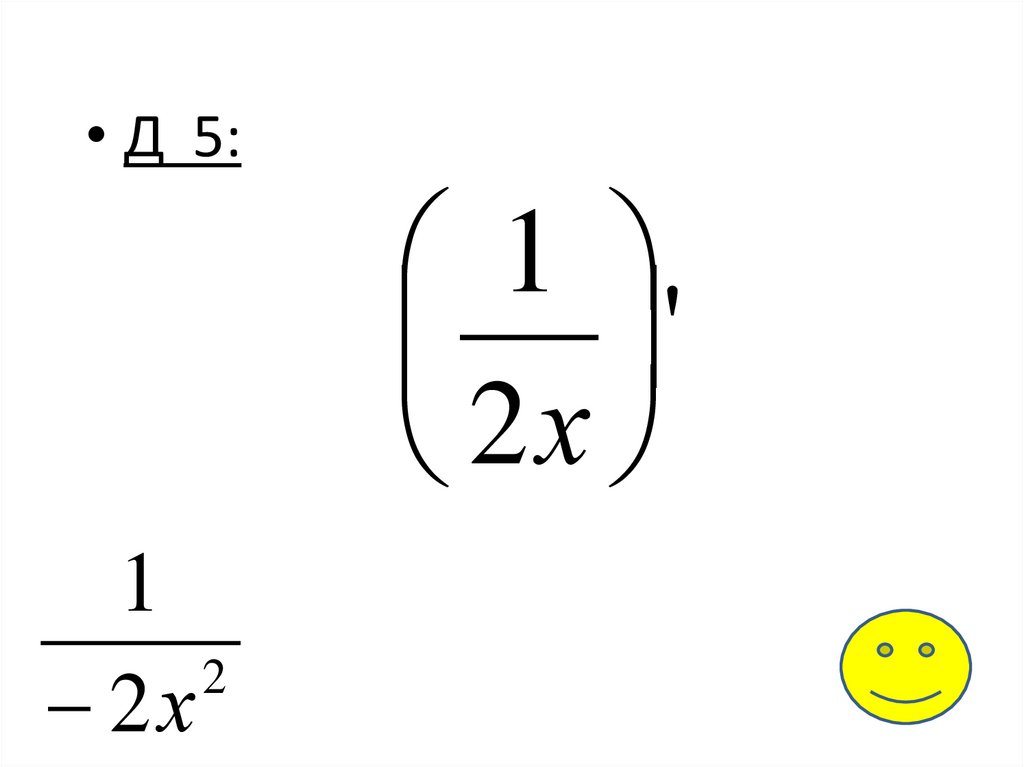


 Математика
Математика








